Introduction
The correct modeling of energy dissipation is a key step to properly estimating the seismic response of buildings. This is most important for steel buildings since energy dissipation is supposed to originate from several sources. The modal spectral dynamic analysis procedures specified in some building codes (NBCC, 2010; EC8, 2004; IBC, 2009) consider the dissipated energy from all sources via an equivalent viscous damper with 5% of critical damping. Therefore, it can be inferred that most building codes do not take into account the variation in dissipated energy from one material to another nor from one source to another. It is worth to mention that there have been a number of investigations where energy dissipation due to plastic deformations is modeled by using an equivalent viscous damping model (Hadjian, 1982; Iwan, 1980; Jennings, 1968; Smyrou et al., 2011; Wijesundara et al., 2011). As it will be presented later in this paper, this practice, as well as that of 5% of equivalent damping considered in the codes, may represent a very crude approximation.
Before proceeding further, it must be stated that many mechanisms may contribute to energy dissipation in real structures. For instance, in relatively simple structural systems like those used in laboratory experiments subjected to small and moderate deformations, most of the energy dissipation sources arise from the thermal effects of repeated elastic straining of the material and from the internal friction between the boundaries of the material grains. On the other hand, in real-scale structures, many other mechanisms may contribute to the energy dissipation process. For example, when a building is subjected to seismic excitations, friction in steel connections must be considered as one of the energy dissipation mechanisms, as well as opening and closing of micro cracks, and friction between the main beam and columns of the structure and nonstructural elements such as partition walls.
Unfortunately, it is impossible to mathematically represent each of the mentioned above (and several others) energy-dissipating mechanisms in real-scale buildings. As a result, following what is documented in building codes (NBCC, 2010; EC8, 2004; IBC, 2009), dissipation of energy is usually modeled in a highly idealized manner. In the particular case of steel buildings, the dissipated energy corresponding to small structural deformations (below the elastic limit) is modeled by a viscous damper while that associated to plastic deformations (within the inelastic range) is taken into account by considering the constitutive relationship of the material. The viscous damper is frequently used because of its mathematical simplicity.
The influence of dissipated energy on the seismic response of structures has been extensively studied for buildings modeled as single degree of freedom (SDOF) systems. Some investigations have also been conducted modeling buildings using somewhat more complex systems, such as shear buildings. However, there are only a few investigations that have dealt with buildings modeled as complex multi-degree-of-freedom (MDOF) systems. The effect of the dissipated energy produced by hysteretic behavior (yielding) of the material as a result of large structural deformations, as well as by elastic viscous damping, on the seismic response of steel buildings, modeled as complex 2D MDOF systems, is evaluated in this paper. Low-, mid- and high-rise buildings are analyzed. Furthermore, the effect is calculated for different levels of structural deformations and for different response parameters. Finally, the practice of expressing the plastic energy effect in terms of viscous damping is discussed and a value of equivalent viscous damping is proposed.
Literature review
The evaluation of the effect of the dissipated energy on the seismic response of steel buildings has been addressed by many researchers during the last decades. In the late sixties, Jennings (1968) investigated the concept of equivalent viscous damping for the steady-state response of simple yielding structures, which were modeled as elasto-plastic oscillators subjected to sinusoidal excitation. It was demonstrated that the results can significantly differ from those of the actual response, depending on the modeling of the resonant frequency shift characteristic of yielding response.
During the early eighties, Iwan (1980) used the inelastic displacement response of SDOF hysteretic structures to determine the effective linear period and damping parameters as a function of ductility. Then a simple empirical equation to estimate the mid-period range inelastic response spectrum of a general hysteretic structure given the linear response spectrum of the excitation was proposed. Newmark & Hall (1982) conducted an investigation to develop an approximated procedure to construct inelastic response spectra. Hadjian (1982) demonstrated in general that, for equivalent linear models for simple yielding systems at comparable ductilities, damping values due to harmonic excitation are about five times those due to earthquake excitation. Pall & Marsh (1982) proposed a new concept for aseismic design of steel framed buildings by providing sliding friction devices in the bracing system of the frames. By using inelastic time history dynamic analyses, they showed the superior performance of the friction damped braced system when compared to the responses of other structural systems.
During the late eighties, Hadjian (1989) computed spectral reductions produced by nonlinear behavior of the material. Miranda & Bertero (1994) developed simplified mathematical expressions to estimate the inelastic design spectra in terms of allowable ductility. Shen & Akbas (1999) suggested several simplified equations to calculate the input and the damping energy of SMRFs under the action of strong motions for different soil conditions. Reyes-Salazar & Haldar (2001a) compared the effect of dissipation of energy due to material plasticization and elastic viscous damping with that of semi-rigid connections. Ramirez et al., (2002a) derived the simplified methods documented in NEHRP 2000 to estimate the peak acceleration and velocity in damped framed systems.
Furthermore, (Ramirez et al., 2002, 2003) presented results regarding the effect of damping and proposed analysis procedures which were included in NEHRP 2000. Arroyo-Espinoza & Teran-Gilmore (2003) carried out a numerical evaluation of the dynamic response of SDOF systems in order to derive expressions to calculate strength reduction factors. Hong & Jiang (2004) reported the effect of the uncertainty in the energy dissipated by damping on the maximum displacement of linear and nonlinear SDOF models. Val & Segal (2005) contributed to studying the differences between responses of SDOF systems with viscous and hysteretic damping using earthquake acceleration time-histories. They observed that the peak displacement responses and energy values between the systems presented significant differences.Levy et al. (2006) employed a linearization method to compute nearly harmonic equivalent stiffness and damping for bilinear systems in the context of earthquake-resistant philosophy. Chopra (2012) examined the relative effect of yielding and viscous damping for structures idealized as SDOF systems; it was found that in general, the effects of yielding should not be considered in terms of a fixed amount of equivalent viscous damping. Ayoub & Chenouda (2009) proposed some response spectra for degrading structural systems under the action of seismic loading. Sanchez-Ricart (2010) conducted a parametric study for SMRFs designed in accordance with Eurocode 3 and 8. They considered overstrength, ductility capacity, force reduction factor as well as zones of plastic redistribution in the structure. Rupakhety & Sigbjörnsson (2009) developed ground-motion prediction equations for ductility demands and spectral displacement of constant-strength elasto-plastic SDOF systems. Gillie et al. (2010) documented the inelastic response of SDOF systems excited by ground motions with forward directivity.
Wijesundara et al. (2011) developed an equivalent viscous damping equation, as a function of the ductility demand and the non-dimensional slenderness ratio, for concentrically braced frame structures based on the hysteretic response of 15 different single story models. Smyrou et al. (2011) studied the implications of using the available damping models on analysis. As a result of a series of considerations, a damping modeling solution for nonlinear dynamic analyses of cantilever RC walls was suggested within the framework of Direct Displacement-Based Design, supported by comparative analyses of wall structures. Rodrigues et al. (2012) carried out an experimental program where 24 columns were tested for different loading histories, under uniaxial and biaxial conditions, focusing the study on energy dissipation and damping capacity. Proposals for estimating the equivalent viscous damping presented by other researchers are compared with the experimental results. Finally, simplified expressions are proposed to estimate equivalent viscous damping in RC columns under biaxial loading.
Moreover, Ganjavi & Hao (2012) compared the responses of elastic and inelastic systems subjected to strong motions recorded on soft soils. Lavan & Avishur (2013) examined the sensitivity of the response of optimally damped frames to uncertainty in structural and damping properties. In general terms, they demonstrated that uncertainties related to nonlinear analysis lead to larger mean drifts than expected, making some designs more sensitive than others. Beheshti-Aval et al. (2013) studied a friction/hysteretic damper installed in the middle of cross bracing for dissipating seismic energy, which during weak to moderate ground motions dissipates energy by friction while during strong ground motions, it absorbs energy by yielding. Stamatopoulos (2014), by using nonlinear dynamic analyses, evaluated the influence of semi-rigid behavior of the steel column base plate on the seismic behavior of steel frames, where yielding of the joint components was considered. It was found that the column base flexibility strongly affects the seismic response in terms of displacements, bending moments, shear forces and plastic hinge formation and therefore should be always considered. Bagheri et al. (2015) studied the performance of a metallic-yielding dampers in steel building frames as well as compared with that of rotational friction dampers, showing that by adding dampers in both systems the structural damages are reduced or removed.
Very recently, Pu et al. (2016) performed a statistical investigation of the damping modification factor (DMF) based on 50 pulse-like near-fault ground motions, which were very carefully selected. Based on the statistical results, empirical formulas for estimating DMF for displacement, velocity and acceleration spectra were proposed, and the effect of structural period, pulse period and damping ratio were considered. Puthanpurayil et al. (2016) reported a new approach to model damping by expressing the damping matrix at an elemental level. The results showed that the proposed models produced more reliable results from an engineering perspective in comparison to the global models. They also documented that the proposed elemental damping models lead to smaller and more realistic damping moments plastic hinge locations. Zahrai & Cheraghi (2017) proposed a Multi-level Pipe Damper, which dissipates energy by yielding. They numerically proved the effectiveness of the damper by nonlinear time-history seismic analyses of 5-, 10- and 15-story steel buildings, observing that the reduction responses in terms of maximum drifts range between 11% and 54%. Sepahvand et al. (2018), presented optimum plastic design procedures using mechanism control for moment steel frames, which is based on the plastic rotation of columns. They showed that the designed frames had high seismic performance. Zand & Akbari (2018) investigated the effects of seven viscous damping models, which were derived by considering different forms of the stiffness matrices, in the seismic demands of moment and concentrically braced steel frames. They concluded that applying Rayleigh damping model, as a default model will produce underestimated responses and that the type of stiffness matrix used in the stiffness proportional damping model is not important. Abadi & Bahar (2018) proposed a reliable equation for design of SMRFs using Displacement-based Design method at the Life Safety performance level and the Equivalent Viscous Damping hypothesis. The results showed an exponential trend that diverges from that of other formulations. Two new relations are proposed for hysteretic damping based on ductility and the ratios of the initial and equivalent periods. Yapıcı et al. (2019), by using numerical and experimental results, analyzed the behavior of steel structures considering the lumped and distributed plasticity models, where the non-linear behavior of the material of steel elements was explicitly provided.
Based on the previous discussion, there is no doubt about the significant contributions to the state of the art regarding the evaluation of the effects of energy dissipation. Most of them, however, are limited to SDOF systems or to plane shear buildings, and in other cases, a limited structural deformation is considered. The effect of viscous damping as well as the hysteretic behavior due to nonlinear deformations of steel buildings of low-, medium- and high-rise, modeled as complex MDOF systems, have not been studied yet. Reyes-Salazar & Haldar, 1999, 2000, 2001) demonstrated that SMRFs are very effective in dissipating earthquake-induced energy, which has a considerable effect on the seismic response. In addition, the relative effects of damping and nonlinear behavior of the material on the seismic response in terms of local and global response parameters for different levels of structural deformations have not been evaluated either. The study of such issues represents a step in the right direction toward the improvement of the design of earthquake-resistant structures.
Objectives
In summary, the main objective of this paper is to evaluate the relative effect of viscous damping and yielding of the material on the reduction of the response of low-, mid- and high-rise steel buildings with perimeter moment resisting frames (PMRF) modeled as complex 2D MDOF systems. To this aim, the linear and nonlinear seismic responses of some steel building models are calculated for several seismic intensities to produce, small, moderate, and significant yielding. The specific objectives addressed in the study are:
Objective 1. Calculate the reduction of the response produced by yielding of the material. Such a reduction is calculated for global parameters, namely drifts, roof displacements, base shear and interstorey shear as well as for local parameters (axial load and bending moments).
Objective 2. Calculate the reduction of the response produced by damping for the same cases considered in Objective 1 and compare it with that of yielding.
Objective 3. Evaluate the accuracy of expressing the effect of dissipated energy by yielding in terms of viscous damping.
Methodology and procedure
To address all the objectives of this paper, the seismic responses of three steel building structures are estimated as accurately as possible by modeling them, as stated earlier, as complex 2D MDOF structures. Therefore, higher mode contributions are explicitly considered. The models are excited by twenty strong ground motions consistent with the seismic hazard of the area where they are located. The Ruaumoko Software (Carr, 2016) is used to carry out the nonlinear time history seismic analyses in order to estimate the seismic response of the steel buildings.
In addition, the Newmark constant average acceleration method, lumped mass matrix and Rayleigh damping are used for each nonlinear dynamic analysis. Also, 3% of viscous damping is assumed in the first two modes for the 3- and 9-level building; the same amount is considered for the 20-level building but for the first and fourth modes instead. One reason for this is that the effective modal masses (EMM) for the 3- and 9-level models are 95% and 91%, respectively, if the first two modes are used. Similarly, for the case of the 20-story model, the EMM associated to the first four modes is 96%. In addition, using these modes will not lead to extremely large damping ratios in the superior modes, particularly for the 20-story model; otherwise, it may result in unrealistic very large damping forces.
The main characteristics of the three buildings will be described in the next section. Large displacement effect is considered in the nonlinear dynamic analysis, and the integration time step used is 0.01 sec. The structural members are modeled as beam-column elements and rigid panel zone is considered. The hysteretic behavior of the members is modeled as bilinear with 3% of post-elastic stiffness. The interaction between axial loads and bending moments is given by the equation (interaction surface) proposed by Chen and Atsuta (1971). Additional details regarding the models, ground motions and energy dissipation sources, are provided in the next sections of the paper.
Structural models
Three steel building models that were particularly designed to be used in the SAC Steel Project (FEMA 335C, 2000) are considered in this paper for numerical evaluation of the issues discussed earlier. Such structures are represented as three PMRF with 3-, 9- and 20-story, respectively. They were designed for Los Angeles Area following the Pre-Northridge recommendations and it is assumed that satisfy the available code requirements at that time (UBC, 1997) the project was developed. The 3-, 9- and 20-level buildings will be denoted hereafter as Models 1, 2 and 3, respectively, their corresponding lateral vibration fundamental periods are 1.03s, 2.38s and 4.07s. The 9- and 20-level buildings have single- and two-level basements, respectively.
The geometry of Models 1, 2 and 3, are shown in Fig. 1, Fig. 2 and Fig. 3, respectively. Information regarding the cross sections of beams and columns, are summarized in Table 1 for Models 1 and 2, while those of Model 3 are presented in Table 2. As stated before, the buildings are represented by complex-2D MDOF systems. Every column of the PMRF is represented by one element; on the other hand, each girder is represented by two elements, having one node at the mid-span. Additionally, three degrees of freedom are assumed at every node.
Table 1 Beam and column sections, PMRF of Models 1 and 2
| Model | Story | Columns | Girders | |
| Exterior | Interior | |||
| 3-Level | 1 | W14×257 | W14×311 | W33×118 |
| 2 | W14×257 | W14×311 | W30×116 | |
| 3/Roof | W14×257 | W14×311 | W24×68 | |
| 9-Level | Basement-1 | W14×370 | W14×500 | W36×160 |
| 1 | W14×370 | W14×500 | W36×160 | |
| 2 | W14×370 | W14×500 | W36×160 | |
| 3 | W14×370 | W14×455 | W36×135 | |
| 4 | W14×370 | W14×455 | W36×135 | |
| 5 | W14×283 | W14×370 | W36×135 | |
| 6 | W14×283 | W14×370 | W36×135 | |
| 7 | W14×257 | W14×283 | W30×99 | |
| 8 | W14×257 | W14×283 | W27×84 | |
| 9/roof | W14×233 | W14×257 | W24×68 | |
Table 2 Beam and column sections, PMRF of Model 3
| Story | Columns | Girders | |
| Exterior | Interior | ||
| Basement-1 | 15×15×2.00 | W24×335 | W14×22 |
| Basement-2 | 15×15×2.00 | W24×335 | W30×99 |
| 1 | 15×15×2.00 | W24×335 | W30×99 |
| 2 | 15×15×2.00 | W24×335 | W30×99 |
| 3 | 15×15×1.25 | W24×335 | W30×99 |
| 4 | 15×15×1.25 | W24×335 | W30×99 |
| 5 | 15×15×1.25 | W24×335 | W30×108 |
| 6 | 15×15×1.00 | W24×229 | W30×108 |
| 7 | 15×15×1.00 | W24×229 | W30×108 |
| 8 | 15×15×1.00 | W24×229 | W30×108 |
| 9 | 15×15×1.00 | W24×229 | W30×108 |
| 10 | 15×15×1.00 | W24×229 | W30×108 |
| 11 | 15×15×1.00 | W24×229 | W30×99 |
| 12 | 15×15×1.00 | W24×192 | W30×99 |
| 13 | 15×15×1.00 | W24×192 | W30×99 |
| 14 | 15×15×1.00 | W24×192 | W30×99 |
| 15 | 15×15×0.75 | W24×131 | W30×99 |
| 16 | 15×15×0.75 | W24×131 | W30×99 |
| 17 | 15×15×0.75 | W24×131 | W27×84 |
| 18 | 15×15×0.75 | W24×117 | W27×84 |
| 19 | 15×15×0.75 | W24×117 | W24×62 |
| 20/Roof | 15×15×0.50 | W24×84 | W21×50 |
Energy dissipation
The energy that is dissipated by yielding of the material is denoted as “E P ”, which represents the work done by the member forces through the corresponding inelastic deformations. The E P term can be expressed as:
where, for a particular inelastic incursion during a specific time step, n is the number of plastic hinges developed in the structural system under consideration; M Pi and P Pi are the bending moment and the axial load, respectively, acting where the plastic hinges are located; θ Pi and H Pi are the corresponding plastic rotations and plastic axial elongations, respectively.
The energy dissipated by viscous damping (E ζ ) during a generic time interval defined by (t1, t2) can be represented as:
Where U 1 and U 2 represent the velocity vectors at initial and final interval time, respectively, C is the damping matrix and U denotes the displacement vector.
In order to estimate the reduction of the response produced only by E P , the ratio (R P ) of the elastic to the inelastic response is used, and it is calculated as follows:
where ζ=3% indicates that 3% of critical damping is considered in both analyses.
For the case of the response reduction produced only for the effect of E ζ , the ratio (R ζ ) of the elastic response without considering viscous damping to the elastic response with 3% of viscous damping is calculated as:
Additional subscripts will be added to the R ζ and R P symbols to distinguish one type of response parameter from another.
Earthquake loading
In order to obtain meaningful results and conclusions and to represent the seismic hazard of the area, the models under consideration are excited by twenty strong ground motions. Such earthquakes were recorded at the site where the models are located and were obtained from the data set of the National Strong Motion Program of the United States Geological Survey.
Table 3 summarizes the main characteristics of the ground motions. It can also be noted in Table 3 that the values of the predominant periods of the records range from 0.13 to 0.72 sec. The models are subjected to the vertical and horizontal components acting at the same time, in addition to the gravity loads. For a particular direction, half of the total seismic loading is applied to the SMRF oriented in the direction under consideration.
Table 3 Strong motion records
| № | Place | Date | Station | T (s) | T (s) | ED | M | PGA (cm/s2) | |
| NS | EW | km | NS | EW | |||||
| 1 | Landers, California | 6/28/1992 | Fun Valley, Reservoir 361 | 0.30 | 0.30 | 31 | 7.3 | 213 | 203 |
| 2 | Mammoth Lakes, California | 5/27/1980 | Convict Creek | 0.19 | 0.14 | 11.9 | 6.3 | 316 | 257 |
| 3 | Victoria | 6/9/1980 | Cerro Prieto | 0.13 | 0.23 | 37 | 6.1 | 613 | 574 |
| 4 | Parkfield, California | 9/28/2004 | Parkfield; Joaquin Canyon | 0.16 | 0.16 | 14.8 | 6 | 609 | 487 |
| 5 | Puget Sound, Washington | 4/29/1965 | Olympia Hwy Test Lab | 0.17 | 0.14 | 89 | 6.5 | 216 | 215 |
| 6 | Long Beach, California | 3/10/1933 | Utilities Bldg, Long Beach | 0.27 | 0.19 | 29 | 6.3 | 219 | 175 |
| 7 | Sierra El Mayor, Mexico | 4/4/2010 | El centro, California | 0.15 | 0.21 | 77.3 | 7.2 | 544 | 496 |
| 8 | Petrolia/Cape Mendocino Cal. | 4/25/1992 | Centerville Beach, Naval Facility | 0.15 | 0.15 | 22 | 7.2 | 471 | 317 |
| 9 | Morgan Hill | 4/24/1984 | Gilroy Array Sta #4 | 0.15 | 0.15 | 38 | 6.2 | 395 | 224 |
| 10 | Western Washington | 4/13/1949 | Olympia Hwy Test Lab | 0.21 | 0.38 | 39 | 7.1 | 295 | 195 |
| 11 | San Fernando | 2/9/1971 | Castaic - Old Ridge Route | 0.21 | 0.33 | 24 | 6.6 | 328 | 280 |
| 12 | Mammoth Lakes, California | 5/25/1980 | Long Valley Dam | 0.56 | 0.16 | 12.7 | 6.5 | 418 | 270 |
| 13 | El Centro | 5/18/1940 | El Centro – Imp Vall Irr Dist | 0.53 | 0.25 | 12 | 7 | 350 | 218 |
| 14 | Loma Prieta, California | 10/18/1989 | Palo Alto | 0.35 | 0.3 | 47 | 6.9 | 378 | 341 |
| 15 | Santa Barbara, California | 8/13/1978 | UCSB Goleta FF | 0.72 | 0.17 | 14 | 5.1 | 361 | 286 |
| 16 | Coalinga, California | 5/2/1983 | Parkfield FaultZone 14 | 0.38 | 1.08 | 38 | 6.2 | 269 | 269 |
| 17 | Imperial Valley, California | 10/15/1979 | Chihuahua | 0.74 | 0.26 | 19 | 6.5 | 262 | 250 |
| 18 | Northridge, California | 1/17/1994 | Canoga Park, Santa Susana | 0.40 | 0.6 | 15.8 | 6.7 | 602 | 397 |
| 19 | Offshore Northern, Calif. | 1/10/2010 | Ferndale, California | 0.60 | 0.35 | 42.9 | 6.5 | 431 | 431 |
| 20 | Joshua Tree, California | 4/23/1992 | Indio, Jackson Road | 0.62 | 0.21 | 25.6 | 6.1 | 400 | 399 |
The deformation of any of the models falls within the elastic range when subjected to any of the strong motion records. To observe the three possible levels of deformation, namely, elastic, moderate nonlinear, and significant nonlinear behavior, they are scaled in terms of S a evaluated in the fundamental vibration period (S a (T 1 )). The values of S a varied from 0.2g to 1.2g for the 3-level model, with increments of 0.2 g, from 0.1g to 0.5g for the 9-level model, and from 0.1g to 0.3g for the 20-level model. The increment for the last two models was 0.1g. Therefore, the maximum values of the seismic intensities are Sa=1.2g, 0.5g and 0.3g for the 3-, 9- and 20-story models, respectively. The average interstorey drifts for the minimum, intermediate and maximum levels of seismic intensity considered were around 0.015, 0.023 and 0.033, respectively.
It can be said that these deformation states correspond approximately to the serviceability, life safety and global collapse limit states, respectively. Even though, as stated above, the maximum average drifts were around 0.033, drifts of around 5% were observed for some seismic records; this state of deformations is very close to that related to a collapse mechanism. This is consistent with the results of some experimental studies where it has been shown that SMRFs may undergo lateral drifts of up to 5% and still vibrate stably without significant loss of strength and stiffness (Bruneau et al., 2018; Leon & Shin, 1995; Nader & Astaneh, 1991; Osman et al., 1995; Roeder et al., 1993; Schneider et al., 1993). In this investigation, a significant number of plastic hinges were observed for some seismic records for this level of deformation.
Gravity loads were also considered in the numerical simulation. They are simultaneously applied with the seismic loading. They are given in Appendix I.
Objective 1. Response reduction produced by yielding
In this part of the paper, the results related to Objective 1, i.e., the response reductions produced by yielding are discussed. Additional subscripts are added to the R P symbol defined earlier to make a difference between seismic response parameters. Furthermore, the letters G and L will represent “global” and “local” seismic responses, respectively. Hence, the parameters R PG,V , R PG,D , and R PG,T will define the reductions in terms of interstorey shears, interstorey displacements (drifts) and top displacements (roof), respectively. Similarly, R PL,A and R PL,M will denote the reductions in terms of local parameters, namely axial loads, and bending moments, respectively, at the base of the columns on the ground level.
Typical results for R PG,V considering the N-S direction of the 3-level model are given in Figs. 4a, 4b and 4c, for seismic intensities (Sa) of 0.2g, 0.6g and 1.0g, respectively. In such figures, the word “SL” represents the story level. The corresponding results for the parameter R PG,D are presented in Figs. 4d, 4e and 4f.

Fig. 4 Response reduction of the 3-level building, NS; (a) R PG,V , Sa=0.2g; (b) R PG,V , Sa=0.6g; (c) R PG,V , Sa=1.0g; (d) R PG,D , Sa=0.2g; (e) R PG,D , Sa=0.6g; (f) R PG,D , Sa=1.0g
It can be observed that for a given story and seismic intensity (greater than 0.2g), the values of R PG,V and R PG,D significantly vary with the strong motion under consideration, although they were normalized similarly; it reflects the influence of frequency contents and higher mode response contribution to the linear and nonlinear structural responses. As it may be expected, the values of both R PG,V and R PG,D , are equal to unity basically in every case for the lowest seismic intensity (Sa= 0.2g) implying no yielding and consequently no reduction of shears nor displacements. However, significant reductions occur for larger seismic intensities; values of up to 3.5 and 2.5 can be observed corresponding to interstorey shears and displacements, respectively, showing a significant effect of the dissipated energy by yielding on the structural response. Thus, these quantities indicate that the elastic interstorey shears and displacements are, for some cases, up to 350% and 250% greater, respectively, than the corresponding values of the inelastic case.
Charts similar to those presented on Fig. 4 were also generated for R PG,V and R PG,D for other seismic intensities, as well as for the EW direction of the 3-level model; considering two response parameters, two directions and six seismic intensities, a total of 24 plots like those given in Fig. 4 were developed but they are not presented in this paper for the sake of brevity. Twelve plots were also developed for R PG,T , but they are not presented as well. A similar set of plots were also developed for the 9- and 20-story models. The discussion is made in all the cases, however, only in terms of the results averaged over all the strong motions, namely in terms of the mean values.
The mean values of R PG,V are presented in Figs. 5a and 5b for the NS and EW directions of the 3-level model, respectively. The corresponding results are given in Figs. 5c and 5d for the 9-story building, while those of the 20-story building are given in Figs. 5e and 5f. Results indicate that for the 3-story model, for a given seismic intensity, the mean values of R PG,V , are fairly constant through the stories in most of the cases, particularly for the first four seismic intensities (Sa=0.1g through 0.8g), but for the 9-level model the mean values tend, in general, to slightly increase with the story number.
In addition, for these two buildings, for a given story number, the variation (increment) in the reduction from one Sa value to another is approximately proportional to the increment of Sa; this variation is different from one story to another. On the other hand, for the case of the 20-level building, the mean values, in general, increase with the story number and the variation in the reduction from one Sa to another tends also to increase with the story number. Thus, the reductions of interstorey shears produced by yielding are significant; the maximum values tend to increase with the building height, they are about 3, 3.5 and 4 for the 3-, 9- and 20-level models, respectively and are quite similar for the NS and EW directions.
Results like those presented in Fig. 5 for R PG,V were also generated for R PG,D . The mean values corresponding to the three buildings, the two horizontal directions, and all the seismic intensities under consideration, are summarized in Fig. 6. Based on the results illustrated in these figures, significant differences and trends can be observed for the mean values of R PG,D from one model to another. For instance, the values of R PG,D for the 3-story building, in general, slightly decrease as the story number increases and they tend to increase with the seismic intensity in most of the cases, particularly in the low range. It can be observed as well that the maximum value (for Sa=1.2g) is about 1.5, which is similar for both the NS and EW directions.

Fig. 5 Mean values of R PG,V ; (a) and (b), NS and EW of the 3-level building; (c) and (d), NS and EW of the 9-level building; (e) and (f), NS and EW of the 20-level building
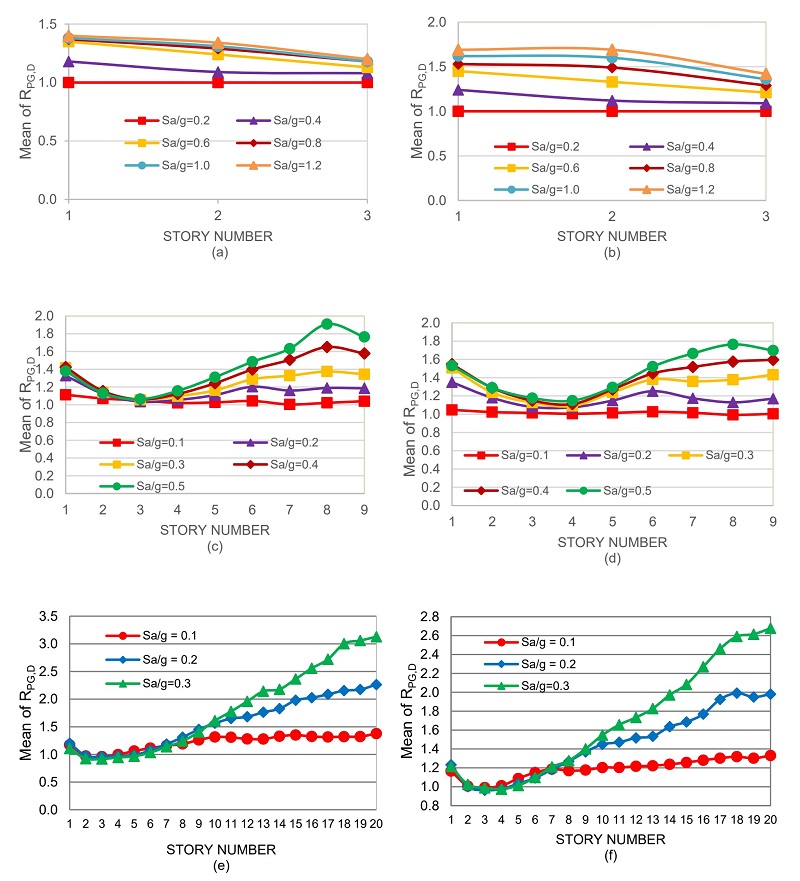
Fig. 6 Mean values of R PG,D ; (a) and (b), NS and EW of the 3-level building; (c) and (d), NS and EW of the 9-level building; (e) and (f), NS and EW of the 20-level building
For the 9-story building, unlike the 3-level model, the mean values tend to decrease from Stories 1 to 3, tend to increase from Stories 4 to 8, and tend to decrease for the top story (roof). The values are equal, or relatively close to each other, for all seismic intensities from Stories 1 through 5, but they increase with Sa for the other stories. The maximum mean value is about 1.8 and is quite similar for both horizontal directions. For the 20-story model the R PG,D mean values tend to decrease from stories 1 through 4, and then R PG,D tend to monotonically increase with the story number from Stories 5 to 20. Also, there is little variation of the mean values with Sa from Stories 1 to 8, but they can significantly vary from the upper stories. This variation (increment) is more significant as the story number increases. The maximum value is about 3 being much larger than that of the 9-story building, which in turn is larger than that of the 3-level building implying that, as for the cases of shears, the maximum values tend to increase with the building height. By comparing the results of Fig. 6 with those of Fig. 5 it is observed that the reduction produced by yielding is much larger for interstorey shears than for interstorey displacements.
The reduction of the response in terms of the roof displacement (R PG,T ) produced yielding is now presented. As stated earlier only the mean values of R PG,T are discussed, they are given in Column (2) of Table 4. As observed for other parameters the reduction of the roof displacement tends to increase with the seismic intensity. However, the maximum reduction values follow an opposite trend than that observed for shear and displacements, i.e., the maximum values tend to decrease with the model height; they are 1.67, 1.45 and 1.35 for the 3-, 9- and 20-level buildings, respectively. The implication of this is that the reduction of the seismic response in terms of two broadly used parameters (and somehow considered similar) to represent the structural deformation, namely interstorey displacements and roof displacements, may be quite different from each other.
Table 4 Reduction of the response due to yielding and damping for individual parameters
| Model | Direction | Sa/g (1) | RPG,T (2) | RPL,A | RPL,M | RζG,T (7) | RζL,A | RζL,M | ||||
| Ext (3) | Int (4) | Ext (5) | Int (6) | Ext (8) | Int (9) | Ext (10) | Int (11) | |||||
| 1 | NS | 0.2 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.57 | 3.04 | 2.72 | 1.82 | 1.81 |
| 0.4 | 1.11 | 1.11 | 1.00 | 1.29 | 1.32 | 1.57 | 3.32 | 3.27 | 1.82 | 1.81 | ||
| 0.6 | 1.25 | 1.22 | 1.01 | 1.67 | 1.80 | 1.57 | 3.41 | 3.55 | 1.83 | 1.81 | ||
| 0.8 | 1.27 | 1.29 | 1.01 | 2.06 | 2.25 | 1.57 | 3.43 | 3.72 | 1.83 | 1.81 | ||
| 1.0 | 1.27 | 1.35 | 1.01 | 2.42 | 2.64 | 1.57 | 3.43 | 3.84 | 1.83 | 1.81 | ||
| 1.2 | 1.29 | 1.42 | 1.01 | 2.75 | 3.00 | 1.57 | 3.43 | 3.93 | 1.83 | 1.81 | ||
| EW | 0.2 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.60 | 2.98 | 2.70 | 1.96 | 1.93 | |
| 0.4 | 1.13 | 1.16 | 1.01 | 1.29 | 1.33 | 1.61 | 3.23 | 3.27 | 1.95 | 1.93 | ||
| 0.6 | 1.34 | 1.27 | 1.01 | 1.68 | 1.81 | 1.61 | 3.33 | 3.57 | 1.95 | 1.93 | ||
| 0.8 | 1.49 | 1.34 | 1.01 | 2.12 | 2.30 | 1.61 | 3.37 | 3.76 | 1.95 | 1.93 | ||
| 1.0 | 1.57 | 1.40 | 1.01 | 2.52 | 2.76 | 1.61 | 3.40 | 3.89 | 1.95 | 1.93 | ||
| 1.2 | 1.67 | 1.44 | 1.01 | 2.92 | 3.19 | 1.61 | 3.41 | 3.98 | 1.95 | 1.93 | ||
| 2 | NS | 0.1 | 1.02 | 1.01 | 1.00 | 1.12 | 1.12 | 1.49 | 2.48 | 2.67 | 1.87 | 1.85 |
| 0.2 | 1.10 | 1.07 | 1.00 | 1.41 | 1.44 | 1.49 | 2.92 | 3.22 | 1.87 | 1.85 | ||
| 0.3 | 1.21 | 1.13 | 1.00 | 1.74 | 1.79 | 1.49 | 3.11 | 3.52 | 1.87 | 1.85 | ||
| 0.4 | 1.33 | 1.18 | 1.00 | 2.05 | 2.10 | 1.49 | 3.22 | 3.70 | 1.87 | 1.86 | ||
| 0.5 | 1.36 | 1.23 | 1.02 | 2.34 | 2.39 | 1.49 | 3.29 | 3.83 | 1.87 | 1.86 | ||
| EW | 0.1 | 1.02 | 1.00 | 1.00 | 1.05 | 1.05 | 1.50 | 2.42 | 2.59 | 1.83 | 1.81 | |
| 0.2 | 1.21 | 1.08 | 1.00 | 1.39 | 1.41 | 1.50 | 2.87 | 3.17 | 1.83 | 1.81 | ||
| 0.3 | 1.35 | 1.16 | 1.01 | 1.69 | 1.73 | 1.51 | 3.10 | 3.49 | 1.83 | 1.81 | ||
| 0.4 | 1.42 | 1.22 | 1.01 | 2.01 | 2.07 | 1.51 | 3.24 | 3.69 | 1.83 | 1.81 | ||
| 0.5 | 1.45 | 1.27 | 1.01 | 2.32 | 2.38 | 1.51 | 3.30 | 3.82 | 1.83 | 1.81 | ||
| 3 | NS | 0.1 | 1.24 | 1.19 | 1.07 | 1.31 | 1.28 | 1.45 | 2.58 | 2.44 | 2.00 | 1.99 |
| 0.2 | 1.32 | 1.50 | 1.24 | 1.78 | 1.78 | 1.45 | 2.76 | 2.75 | 2.00 | 1.99 | ||
| 0.3 | 1.35 | 1.79 | 1.30 | 2.26 | 2.24 | 1.45 | 2.83 | 2.89 | 2.00 | 1.99 | ||
| EW | 0.1 | 1.11 | 1.15 | 1.05 | 1.29 | 1.24 | 1.50 | 2.67 | 2.33 | 1.95 | 1.93 | |
| 0.2 | 1.27 | 1.42 | 1.18 | 1.69 | 1.68 | 1.50 | 2.93 | 2.71 | 1.96 | 1.93 | ||
| 0.3 | 1.35 | 1.64 | 1.19 | 2.12 | 2.19 | 1.50 | 3.04 | 2.87 | 1.96 | 1.93 | ||
The mean values of the reduction of the response due to yielding in terms of both axial loads (R PL,A ) and bending moments (R PL,M ) at interior and exterior base columns are given in columns 3 to 6 of Table 4. For every single case, the magnitude of the reduction increases as the seismic intensity becomes higher. Results indicate that the maximum mean values of R PL,A for exterior columns are 1.44, 1.27 and 1.79 for the 3-, 9-, and 20-story buildings, respectively. Conversely, the values for interior columns are much smaller, being essentially equal to unity for the 3- and 9-story models. Some reasons justifying the above results may be: (1) in the elastic or inelastic analysis required to calculate R PL,A (see Eq. 3), the axial load is coming from the effect of gravity loads (AG), the seismic vertical component (ASV) and the horizontal seismic component (ASH), (2) for interior columns, in general, ASH is larger for elastic than for inelastic analysis, (3) the combined AG + ASV value, however, is essentially the same for elastic and inelastic analysis, which in turn is much larger than ASH, and (4) it produces the R PL,A ratio to be very close to unity.
The mean values of R PL,M are significantly larger than those of R PL,A and they are quite similar for interior and exterior columns. The maximum values are 3.19, 2.39 and 2.26 for the 3-, 9- and 20-story buildings, respectively. Thus, the reduction magnitude may be quite different, not only from one global response parameter to another, but also from one local response parameter to another. The maximum reductions occur for interstorey shears, followed by those of bending moments, interstorey displacements, roof displacements and axial loads.
Objective 2. Response reduction produced by damping
Similar to the case of response reductions produced by yielding, additional subscripts are added to the R ζ symbol defined earlier to distinguish one seismic response parameter from another. Hence R ζG,V , R ζG,D , and R ζG,T represent the reductions produced by damping in terms of interstorey shears, interstorey displacements and top displacements, respectively. Similarly, R ζL,A and R ζL,M will denote the reductions induced by damping in terms of axial loads and bending moments at the base of the columns, respectively. The mean values of R ζG,V and R ζG,D , for all cases, are given in Figs. 7 and 8, respectively.
Unlike what occurred for yielding reduction, as stated in typical structural dynamics textbooks for SDOF systems, reductions due to viscous damping occur even for small levels of deformations. It is also shown that the magnitude of the mean values of both R ζG,V and R ζG,D does not depend on Sa/g and does not significantly vary with the story number. The variation is not significant from one model to another either. For the case of R ζG,V the maximum mean values are 2, 2.5 and 3 for the 3-, 9- and 20-level buildings, respectively. The corresponding maximum mean values for R ζG,D are 1.9, 2.2 and 2.6. Thus, unlike the reduction caused by yielding, the reduction by damping is quite similar for shear and interstorey displacements and is essentially uniformly distributed throughout the structure. These results imply that expressing the effect of yielding in terms of viscous damping, as considered in many seismic codes, may introduce significant errors in the estimation of the structural response.
The mean values of R ζG,T are summarized in Column (7) of Table 4. Similar to the case of interstorey displacements, the reduction in top displacements produced by viscous damping is essentially uniformly distributed through the stories and presents little or no variation with the seismic intensity and the story number or from one model to another. The maximum values are about 1.61, 1.51 and 1.50 for the 3-, 9-, and 20-level models, respectively, which are smaller than those of interstorey drifts (R ζG,D ). The results for R ζL,A and R ζL,M are presented in Columns (8) through (11) of Table 4. It is observed that the mean values of R ζL,A , unlike R ζG,V , R ζG,D and R ζG,T , tend to increase with Sa; the maximum values are 3.98, 3.83 and 2.89, for the 3-, 9- and 20-level models, respectively, and unlike the case of R PL,A , they are quite similar for interior and exterior columns. For the case of bending moments, the maximum mean values are 1.95, 1.87 and 2.00, for the 3-, 9- and 20-level, respectively and, as for the case of axial load, they are quite similar for exterior and interior columns. Thus, the maximum response reductions produced by viscous damping occur for axial loads followed by those of bending moments, interstorey shears, interstorey displacements and roof displacements.
By comparing the magnitude of the response parameter reductions produced by damping with the corresponding reductions produced by yielding it is observed that the reductions are larger for yielding for the case of interstorey shears and for bending moments; however, they are larger for damping for the case of axial load while they are quite similar for the case of interstorey displacements and roof displacements. These results corroborate once more that the response reduction produced by yielding may be qualitatively and quantitatively different from that of damping.

Fig. 7 Mean values of R ζG,V ; (a) and (b), NS and EW of the 3-level building; (c) and (d), NS and EW of the 9-level building; (e) and (f), NS and EW of the 20-level building
Objective 3. Expressing the effect of dissipated energy by yielding in terms of viscous damping
It was discussed in Section 1 of this paper that in many seismic codes, the dissipated energy produced by all sources in steel or concrete buildings is usually considered through a viscous damper with 5% of critical damping. In light of the results obtained in this paper, the accuracy of this practice is evaluated. To this aim, first, the reduction of the response for all the parameters under consideration is firstly calculated for several additional amounts of viscous damping, namely ζ=6%, 9% and 12%, and then the required amount of viscous damping (ζ ,E ) to produce the same average reduction as that of yielding of the material is established. In other words, plots for R ζG,V and R ζG,D (similar to those of Figs. 7 and 8, respectively) as well as for R ζG,T , R ζL,A , R ζL,M (similar to those of Columns 7 to 11 of Table 4 were developed for 6%, 9% and 12% of viscous damping and then the ζ ,E values for all the response parameters under consideration, using the same reduction by yielding and damping, are calculated. They will be denoted hereafter by ζ EG,V , ζ EG,D , ζ EG,T , ζ EL,A and ζ EL,M for interstorey shears, interstorey displacements, roof displacements, axial loads and bending moments, respectively. Only the intensity levels that produce the maximum structural deformations, namely Sa=1.2g, 0.5g and 0.3g for the 3-, 9- and 20-level models, respectively, are considered.
The above-mentioned procedure is illustrated in detail by the following example. For the particular case of interstorey shears and the NS direction of the 3-level model (see Fig. 5a), the average reduction produced by yielding considering all the stories for the maximum deformation (Sa=1.2g) is 2.76. It is observed in Fig. 7a that the corresponding average shear reduction produced by 3% of viscous damping is 1.74. Thus, a value of viscous damping larger than 3% is obviously required to produce an average reduction of 2.76. It is found from the additional results (not shown in this paper) that approximately a viscous damping of 10.5% will produce the same reduction as that of yielding. The above procedure is repeated for all cases and the results are presented in Table 5.
Table 5 Values of the ζ ,E parameter in percentage
| Model | Direction | ζEG,V | ζEG,D | ζEG,T | ζEL,A | ζEL,M | ||
| Ext | Int | Ext | Int | |||||
| 1 | NS | 10.5 | 1.4 | 1.5 | 0.5 | 0.0 | 9.4 | 13.9 |
| EW | 8.6 | 2.4 | 3.5 | 0.5 | 0.0 | 7.7 | 9.6 | |
| 2 | NS | 6.7 | 1.5 | 2.2 | 0.3 | 0.0 | 5.1 | 5.6 |
| EW | 5.8 | 1.6 | 2.6 | 0.4 | 0.0 | 4.8 | 5.4 | |
| 3 | NS | 8.9 | 2.7 | 2.3 | 1.3 | 0.6 | 4.1 | 4.0 |
| EW | 6.0 | 2.1 | 2.1 | 0.9 | 0.5 | 3.6 | 4.3 | |
The results of the table permit making several important observations. For example, it can be established that the values of ζ ,E significantly vary with respect to the model height, the response parameter, and the structural element location. Also, the ζ EG,V values range from 6% to 10.5%, while those of ζ EG,D and ζ EG,T range from 1.2% to 3.0%. For the case of ζ EL,A for exterior columns, the values range from 0.3% to 1.1% while the corresponding values of ζ EL,A are zero o very close to zero for interior columns.
Finally, the values range from 3.6% to 13.9% for ζ EL,M . The above results indicate that the assumption of 3% of viscous damping to represent the reduction response produced by yielding of the material, is reasonable for interstorey and top displacements, very conservative for interstorey shears and bending moments, and very unconservative for axial loads. A value of 5% can conservatively be used for interstorey shears and bending moments and at most 1% should be used for axial loads.
Conclusions
The results of a numerical study regarding the evaluation of the reduction of the response, produced by yielding and viscous damping, of steel buildings modeled as complex multi-degree-of-freedom systems, are presented in this study. Three Steel Moment Resisting Frames (SMRFs) models representing low-, mid, and high-rise buildings and twenty recorded strong ground motions are used in the study. The mean values of the response reductions produced by yielding of the material and viscous damping are calculated for interstorey shears, lateral drifts, roof displacements, and axial loads and bending moments at the base columns. Then, the reductions produced by yielding are expressed in terms of viscous damping. The main findings are summarized as follows:
The response reduction may significantly vary with the seismic ground motion, story level, building height, response parameter, and level of deformation.
The maximum reduction produced by yielding of the material occurs for interstorey shears, followed by those of bending moments, interstorey displacements, roof displacements, and axial loads. For example, inelastic interstorey shears may be up to 300% smaller compared to that of elastic shears, but for the case of axial loads this amount is about 0% and 70% for interior and exterior columns, respectively, showing important limitations of the lateral static and modal analysis seismic methods where both, elastic interstorey shears and forces acting on members, are reduced by the same numerical amount. These results imply that using simplified procedures may lead to very unconservative designs.
The comparison of the magnitude of the response reduction caused by damping with that of yielding of the material demonstrates that the reductions produced by the latter are larger for the case of interstorey shears and bending moments. However, the reductions caused by damping are larger for the case of axial loads and are quite similar for interstorey displacements and roof displacements.
Expressing the reductions of the response produced by yielding in terms of a fixed amount of viscous damping (equivalent), as usually adopted in seismic codes, may result in inappropriate approximation. The equivalent amount of viscous damping depends, in general, on the response parameter under consideration. This practice results in a reasonable approximation for interstorey and roof displacements, in a very conservative design for interstorey shears and bending moments, but in unconservative designs for the case of axial loads. A value of 5% can conservatively be used for interstorey shears and bending moments and at most 1% should be used for axial loads.











 nueva página del texto (beta)
nueva página del texto (beta)






