1. Introduction
Photometric and spectroscopic observations of eclipsing binaries are the essential key to derive absolute parameters of each component, such as stellar masses, radii, and effective temperatures. These parameters are vitally important to understand the evolutionary stage of eclipsing binary systems. In addition, the period analysis of such systems via O − C diagrams, allows us to investigate the underlying physics of the orbital period changes. The O − C diagram is one of the most powerful diagnostic tools to study the dynamical evolution of close binaries. Such analyses tell us whether the binary systems are multiple star systems or not. Multiple systems play an important role in the evolution of binary stars. Most binaries and single stars actually originate from the decay of multiple systems due to internal instabilities and external perturbations (Bate 2004; Bodenheimer 2011; Goodwin & Kroupa 2005; Larson 2001). Therefore their components strongly interact, leading to tidal captures, collisions, fragmentation processes or mergers. These systems also provide significant opportunities to study the dynamical interaction andformation mechanisms of stellar and planetary systems.
Nowadays, thousands of eclipsing binaries have been discovered, but their light curves and physical parameters have not been analysed due to the lack of spectroscopic observations. To alleviate this deficiency we performed Wilson-Devinney (Wilson & Devinney 1971) modelling of VX Lac, based on the photometric and spectroscopic data of the system. Though there are several studies on the light curve of this system in the literature, none of them include spectroscopic data. We have analysed photometric and spectroscopic observations simultaneously for the first time, and we present the fundamental parameters of the system.
VX Lac (BD+37°4662, GSC 03214 − 01295) is an Algol type eclipsing binary star with a visual magnitude of mV ≈ 10.5 and an orbital period of P ≈ 1.07 days. The spectral type of the system was first derived as F0 by Cannon (1934). Subsequently, the spectral type has been estimated to be F0 + K4 IV by Svechnikov & Kuznetsova (1990) using the available online data for VX Lac. The first light-curve of VX Lac was obtained by Szafraniec (1960), determined from visual observations. The first O − C diagram was published by Kreiner (1971), but he could not identify any period variation due to an insufficient number of minima times. The most recent period study of this system was performed by Zasche et al. (2008). They obtained the best solution by assuming a third body approximation (light-time-effect: LITE) and mass transfer. The conservative mass transfer rate was derived as
2. Observations
Photometric CCD observations of VX Lac were carried out with the 40 cm Kreiken Telescope at Ankara University Kreiken Observatory (AUKR1) in 2014. The log of these observations is given in Table 1. The multicolor photometric data of the target were obtained using Johnson-Cousins BV RI filters. All the images were reduced using the relevant tasks of the IRAF2 software in the standard way (bias, dark, and flat correction). We then performed aperture photometry by using the apphot package in IRAF. The individual differential magnitudes were computed in the sense variable minus comparison, whose variability was checked with the help of the observations of a check star. The average errors of those observations were estimated to be ± 0.007, ± 0.004, ± 0.003, and ± 0.003 in the BV RI filters, respectively. The relevant catalog data for the target, comparison, and check stars are summarized in Table 2. These differential magnitudes were used to construct BV RI light curves of the system and were phased using the light elements (see Table 3) calculated from newly observed data together with archival times of minima (see Figure 1).
Table 1 The log of CCD observations
| Obs. dates | Nightly mean errors [mag] | |||
| σB | σV | σR | σI | |
| 21 Jul 2014 | 0.009 | 0.004 | 0.003 | 0.002 |
| 22 Jul 2014 | 0.006 | 0.005 | 0.004 | 0.004 |
| 29 Jul 2014 | 0.004 | 0.003 | 0.004 | 0.005 |
| 24 Aug 2014 | 0.006 | 0.003 | 0.003 | 0.003 |
| 25 Aug 2014 | 0.003 | 0.006 | 0.003 | 0.003 |
| 27 Aug 2014 | 0.008 | 0.003 | 0.002 | 0.005 |
| 31 Aug 2014 | 0.009 | 0.004 | 0.004 | 0.003 |
| 01 Sept 2014 | 0.009 | 0.002 | 0.005 | 0.002 |
Table 2 Observational properties of variable, comparison, and check stars
| Variable | Comparison | Check | |
| VX Lac | GSC 03214-00674-1 | BD+37°4661 | |
| α2000 | 22h42m00s .56 | 22h41m26s.00 | 22h40m58s.29 |
| δ2000 | +38°19’20’’ | +38°20’55’’ | +38°12’11’’ |
| Spec. Type | F0 | - | - |
| B-V | 0.36 | 1.2 | 0.45 |
| mV | 10m.51 | 10m.25 | 11m.05 |
Table 3 The light elements used in computation of the orbital phases
| Reference | Reference epoch | Orbital period |
| T0(HJD + 2450000.) | Porb (days) | |
| This study | 6542.88574 | 1.0744984 |
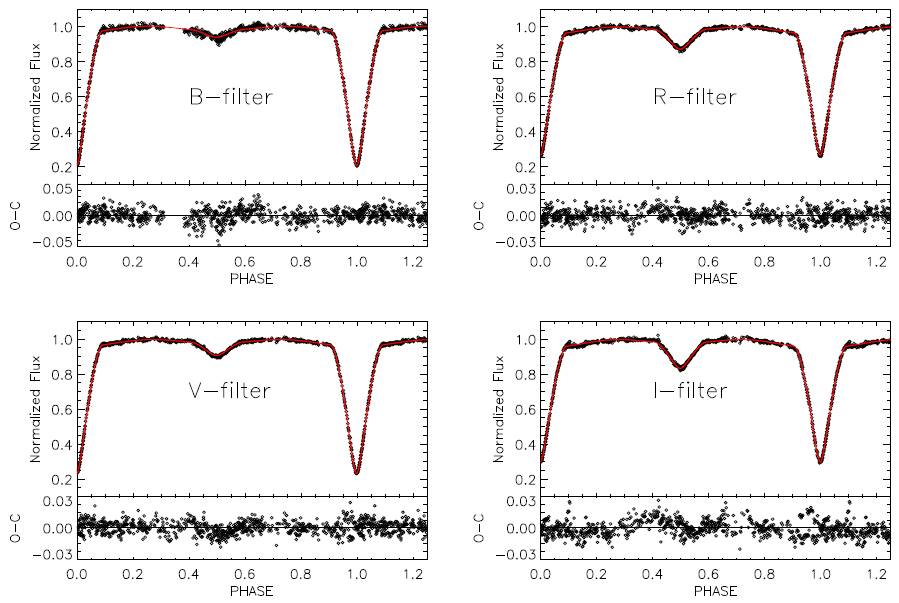
Fig. 1 Observational (diamond) BV RI light curves of VX Lac and best computed model (solid lines) using Mode 5 of W-D . Residuals from the theoretical fits are indicated at the bottom of each passband.
Spectroscopic observations of VX Lac were obtained at the Dominion Astrophysical Observatory (DAO) in Victoria, British Columbia, Canada using the Cassegrain spectrograph attached on the 1.85 m Plaskett telescope. The spectra covered a wavelength region from 5000 Å to 5260 Å with a resolving power of R ≈ 10000. The reductions (cosmic ray, median background fitting and subtraction for each wavelength, aperture summation, and continuum normalization) were performed using the RaVeRe software (Nelson 2010). The same software was used for wavelength calibration and linearisation using the FeAr spectra as wavelength standards.
In order to obtain radial velocity measurements, we applied Rucinski’s broadening functions (Rucinski 2004; Nelson et al. 2006) and standard Fe I lines at 5041.755, 5167.487, 5171.585, 5227.15 Å were used in the radial velocity determinations. We phased these observations with the same light elements that we used to calculate orbital phases of our photometric measurements, after having converted all the observation times to heliocentric values. We found the gamma velocity (Vγ) of the system to be 5.23 ± 0.6 km s-1. The resultant radial velocity curves for each component and the best fits to them are given in Figure 3. We determined semiamplitudes of the fitted curves (K1 and K1) and computed the spectroscopic mass ratio of the system (q = M2/M1 = K1/K2 = 0.27).
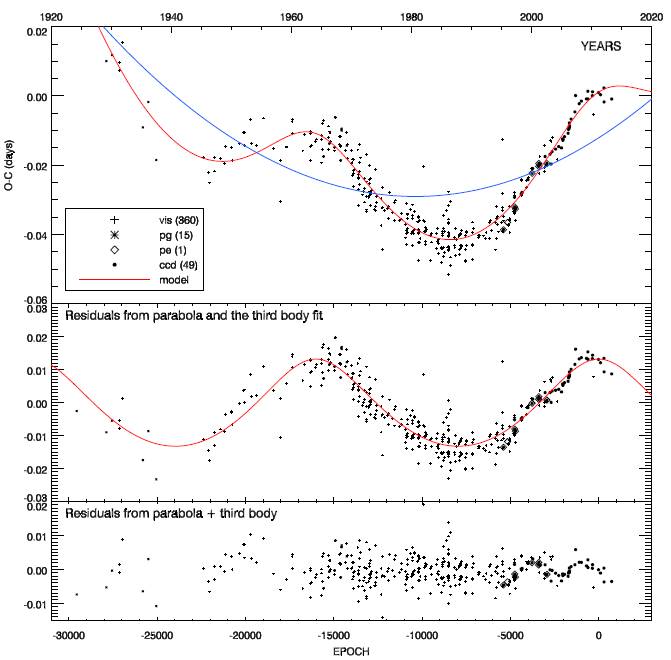
Fig. 2 The (O-C) diagram and best fit model for VX Lac. The solid blue line represents a parabolic fit and the solid red line the LITE model. Observation methods are also shown inside the legend, with counts in parentheses. The color figure can be viewed online.
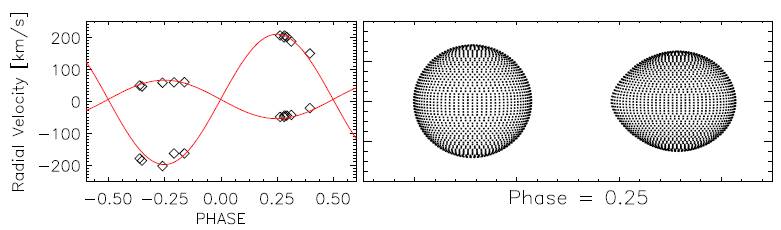
Fig. 3 (Left:)Radial velocity data for VX Lac (see Table 6) and the best fits as solid lines, (Right:) The graphic representation of the model at the orbital phases 0.25.
3. Light and radial velocity curve analysis
Light and radial velocity curves were analysed simultaneously using the Wilson-Devinney code (Wilson & Devinney 1971) (hereafter W-D) to derive the photometric and physical parameters of the components of VX Lac. The analyses were performed in Mode 2 (detached configuration) and Mode 5 (semidetached configuration with the secondary filling its Roche lobe) of the W-D code. During the analyses we fixed the primary component temperature at T1 = 7300 K according to the effective temperature versus spectral type calibration of main-sequence stars by Gray & Corbally (1994). Besides, several parameters were also fixed or calculated during the light curve modelling: the values for the albedo and gravity darkening coefficients, and the limb darkening coefficients were adopted from the tables in van Hamme (1993) as functions of the temperature and wavelength. Bolometric albedos of the components were assumed to be A1 = 1.0 and A2 = 0.5, and gravity darkening coefficients were adopted as g1 = 1.0 and g2 = 0.32, for stars with radiative and convective envelopes, respectively (von Zeipel 1924; Lucy 1967). The adjustable parameters are the mass ratio q, the orbital inclination i, the effective temperature of the secondary T2, the potential of the components Ω1 and Ω2, and the monochromatic luminosity of the primary star L1.
After several trials, two equally plausible solutions emerged: one using Mode 5 and the other, Mode 2, with the latter entailing the secondary very nearly filling its Roche lobe. In view of the fact that the O − C analysis implies conservative mass transfer between components, only Mode 5 is plausible and therefore it is adopted. Our best fit model for Mode 5 is in good agreement with the observed light curves except for just small discrepancies in the phase range between 0.30 and 0.6. These distortions are caused by the data obtained at the beginning of the night, when the air-mass is largest. Even so, we tried to fit these distortions assuming a cool or hot spot on the components. When a cool or hot spot on one of the components was assumed, the solution did not converge. In addition, third light was also tested since there is a strong case for a third star (based on the O − C analysis), but the estimated contribution of third light is less than the error estimates and therefore not significant. The results derived from the light curve modelling are presented in Table 4, while model light curves along with observations are shown in Figure 1.
Table 4 Results of the simultaneous light and radial velocity curve analysis
| Quantity | Mode 2 | Mode 5 |
| q = M2/M1 | 0.26 ±0.01 | 0.27 ±0.03 |
| K1[kms−1] | 54.52 ±2.65 | 55.58 ±2.85 |
| K2[kms−1] | 209.70 ±3.01 | 208.27 ±3.13 |
| γ[kms−1] | 5.28 ±0.66 | 5.23 ±0.67 |
| a[R⊙] | 5.55 ±0.03 | 5.55 ±0.03 |
| T1[K] | 7300 | 7300 |
| T2[K] | 4312 ±44 | 4316 ±46 |
| i[◦] | 86.5 ±0.5 | 85.9 ±0.6 |
| A1 | 1.0 | 1.0 |
| A2 | 0.5 | 0.5 |
| g1 | 1.0 | 1.0 |
| g2 | 0.32 | 0.32 |
| Ω1 | 3.85 ±0.02 | 3.87 ±0.02 |
| Ω2 | 2.41 ±0.03 | 2.39 |
| f1 | -8.5 | -8.7 |
| f2 | -0.1 | 0.0 |
| l1/(l1 + l2)[B] | 0.97 ±0.02 | 0.97 ±0.02 |
| l1/(l1 + l2)[V] | 0.91 ±0.01 | 0.94 ±0.01 |
| l1/(l1 + l2)[R] | 0.94 ±0.02 | 0.90 ±0.01 |
| l1/(l1 + l2)[I] | 0.87 ±0.02 | 0.86 ±0.01 |
| x1,2[B] | 0.786; 0.823 | 0.786; 0.822 |
| x1,2[V] | 0.686; 0.714 | 0.686; 0.713 |
| x1,2[R] | 0.584; 0.599 | 0.584; 0.599 |
| x1,2[I] | 0.488; 0.496 | 0.489; 0.496 |
| y1,2[B] | 0.300; 0.285 | 0.301; 0.286 |
| y1,2[V] | 0.294; 0.267 | 0.294; 0.268 |
| y1,2[R] | 0.290; 0.252 | 0.290; 0.254 |
| y1,2[I] | 0.272; 0.239 | 0.272; 0.240 |
| M1[M⊙] | 1.57 ±0.02 | 1.57 ±0.02 |
| M2[M⊙] | 0.42 ±0.03 | 0.44 ±0.02 |
| R1[R⊙] | 1.56 ±0.02 | 1.55 ±0.02 |
| R2[R⊙] | 1.48 ±0.03 | 1.51 ±0.03 |
| L1[L⊙] | 6.35 ±0.04 | 6.37 ±0.03 |
| L2[L⊙] | 0.67 ±0.02 | 0.68 ±0.03 |
| log g1[cgs] | 4.24 ±0.01 | 4.23 ±0.01 |
| log g2[cgs] | 3.72 ±0.01 | 3.71 ±0.01 |
| Σ(O − C)2[B] | 0.0785 | 0.0811 |
| Σ(O − C)2[V] | 0.0394 | 0.0322 |
| Σ(O − C)2[R] | 0.0313 | 0.0344 |
| Σ(O − C)2[I] | 0.0477 | 0.0499 |
Note: Σ(O − C)2 - final sum of squares of residuals between observed and synthetic light curves; q = M2/M1 - mass ratio of the components, K1,2 - radial velocity amplitudes; γ - radial velocity of the center of mass; g1,2, A1,2 - gravity-darkening and albedo coefficients; T1,2 - temperature of the primary and secondary; i - orbit inclination (in arc degrees); x1,2, y1,2 - non-linear [B; V ;R; I] logarithmic limb-darkening coefficients; Ω1,2 - dimensionless surface potentials; f1,2 - filling factor for the critical Roche lobe; l1/(l1 + l2) - [B; V ;R; I] fractional luminosity of the primary star; M1,2[M⊙], R1,2[R⊙], L1,2[L⊙] - stellar masses, mean radii and luminosity of stars in solar units,; log g1,2 - logarithm (base 10) of the mean surface gravity (cgs unit); and a[R⊙] - orbital semi-major axis in units of solar radius.
4. Period variations
The period analysis of VX Lac was performed using all available minima times in the literature (Paschke & Brat 2006) (O − C gateway3) and combining our new times of minimum light. The O − C diagram of the system was derived using the minima based on the ephemeris given in Table 3. The first panel of Figure 2 clearly shows that VX Lac has a cyclic variation that can be attributed to the LITE due to a physically bound additional component to the system. We modelled the relation using Irwin’s (1959) LITE formulation but could not get a satisfactory fit with those equations alone. Residuals from the LITE fit also indicate that the secular period increases and this phenomenon can be explained via a mass exchange/loss mechanism in the system. Consequently, the best solution was obtained using LITE and a parabolic fit, with which both cyclic and secular variations can be modelled. Assuming that the orbit of the third body is coplanar, we obtained a minimum third body mass M3 = 0.31M⊙.
The distance is computed based on the apparent magnitude taken from the SIMBAD4 database and from the computed absolute magnitudes, with correction for the interstellar extinction AV. The interstellar extinction values AV in the V passband were computed using the reddening value estimated from the infrared dust emission maps of Schlegel et al. (1998) and assuming the extinction to reddening ratio to be 3.1. The bolometric corrections were taken from the Flower (1996) tables. The dynamical parallax derived in that way yielded a distance of 330 ± 14 pc which is the first distance estimate for VX Lac in the literature. According to this result, the mean angular separation between the third body and the eclipsing pair would be about 0’’.05, which is too small for observational detection. If the third star is a main-sequence star, then by using the mass luminosity function for main-sequence stars given by Demircan & Kahraman (1991) the third body would be about 6.5 mag fainter than the VX Lac system, which is too faint for photometric or spectroscopic detection.
Under the assumption of conservative mass transfer between the components of the system, the mass transfer rate was determined as dM/dt = 1.86 × 10−8 M⊙yr−1 (from less massive to more massive). Also, the residuals from the quadratic and third body model indicate an additional cyclic variation as can be clearly seen from the third panel of Figure 2. The cyclic oscillation in the O − C residuals of VX Lac may be attributed one of two things: either there is a fourth body in the system, or there is a significant magnetic activity. If we assume a fourth body, the derived LITE parameters indicate that the orbits of all the stars lie in same plane. For the magnetic activity cycle we used the amplitude and period of the cyclic variation and calculated the pertinent parameters with Applegate’s (1992) formulation as in Table 5, assuming that the secondary component is the active one, considering its spectral type (K4IV). In the case of a magnetic activity cycle, we obtained the subsurface magnetic field of the secondary component as 9.4kG and the brightness variation of the secondary component to be ∆m = 0.03 mag. Such brightness variations can only be detected with long-term high precision photometric observations. Applegate (1992) has shown that any cyclic change in the activity level of one component in a binary system can produce cyclic variation in the orbital period of the system. All the parameters derived from the O − C analysis are given in Table 5.
Table 5 Results from the o-c analysis
| Parameters | Value | err | |
| third body | T0[HJD] | 2455799.333 | ±0.006 |
| P[days] | 1.0744975 | ±0.0000004 | |
| a12,3sini3[AU] | 2.29 | ±0.63 | |
| e3 | 0.24 | ±0.04 | |
| ω3[°] | 87 | ±8 | |
| P3[years] | 47.2 | ±0.3 | |
| A3[days] | 0.0132 | ±0.0003 | |
| f(m3)[M⊙] | 0.0054 | ±0.004 | |
| M3[M⊙] | 0.31 | ±0.02 | |
| fourth body | a12,4sini4[AU] | 0.32 | ±0.04 |
| e4 | 0.31 | ±0.04 | |
| ω4[°] | 34 | ±8 | |
| P4[years] | 7.9 | ±0.01 | |
| A4[days] | 0.0017 | ±0.0002 | |
| f(m4)[M⊙] | 0.00052 | ±0.0015 | |
| M4[M⊙] | 0.13 | ±0.02 | |
| magnetic activity | ΔP[scycle−1] | 0.348 | ±0.028 |
| ΔJ[gcm2s−1] | 1.29·1047 | ±2.11 1045 | |
| ΔE[erg] | 5.36·1040 | ±1.72 1038 | |
| ΔL[ergs−1] | 6.69·1032 | ±3.08 1030 | |
| Δm[mag] | 0.026 | ±0.007 | |
| B[kG] | 9.4 | ±0.3 | |
| mass transfer rate | dM/dt[M⊙yr−1] | 1.86E − 8 | ±8.09E − 10 |
Table 6 Radial velocity data of vx lac
| HJD+2450000 | RV1 [km/s] | err | RV2 [km/s] | err |
| 56905.8995 | 59.60 | 2.33 | -163.22 | 4.82 |
| 56906.9244 | 59.24 | 2.33 | -163.59 | 4.82 |
| 56907.9438 | 57.85 | 2.70 | -202.90 | 4.77 |
| 56908.9204 | 46.21 | 2.85 | -185.87 | 3.72 |
| 56909.7223 | -21.53 | 2.29 | 149.64 | 2.54 |
| 56909.9836 | 49.37 | 1.36 | -179.25 | 1.17 |
| 56910.6546 | -49.08 | 1.50 | 205.90 | 6.30 |
| 56910.6760 | -44.34 | 1.52 | 205.87 | 1.95 |
| 56911.7481 | -49.06 | 1.38 | 199.97 | 3.55 |
| 56912.8355 | -44.98 | 1.38 | 201.40 | 4.56 |
| 56912.8572 | -42.91 | 1.33 | 186.70 | 1.02 |
5. Discussion and conclusion
In this study, four colour BV RI light curves of the eclipsing binary VX Lac were simultaneously analysed using the W-D code. The photometric data were combined with the radial-velocity data in order to obtain fundamental parameters of the components. Furthermore, the orbital period variation of VX Lac was studied.
We obtained identical light curve solutions for both the detached (Mode 2 in W-D code) and the semi-detached mode (Mode 5). According to the Mode 2 solutions, the system is detached, and the secondary component nearly fills its inner Roche lobe. On the other hand, the (O − C) diagram of VX Lac shows a secular period increase, which means that the mass transfer may be occurring from the secondary component to the primary. This result strengthens our findings that VX Lac is a semidetached binary with a mass ratio of q = 0.27. Taking advantage of a simultaneous analysis using four colour light curves plus RV data, we were able to determine the absolute parameters of the system, summarized in Table 4. The present analysis showed that no spot modelling is needed to fit light curves. The effective temperature of the secondary was obtained. It is as about 4300 K, significantly lower than that of the primary and indicates that it is a K0 IV star. Therefore, its contribution to the total system light is less than 1%. Hence, any spotted areas on the secondary would lead to comparatively small photometric effects.
The periodic variation seen in the the (O − C) of VX Lac was attributed to the LITE due to an unseen third body, physically bound to the system, with a period of 47.7 yr. The parameters of the third body are given in Table 5. Using the absolute parameters of the components and assuming an orbit coplanar with the binary, we found that the minimum mass of the third body is M3 = 0.31M⊙.These parameters (mass of the third body and period) are consistent with those obtained by Zasche (2016). The (O − C) diagram also shows that the long-term secular variation is a consequence of the long-term orbital period increase, which can be explained as a mass transfer from the less massive component to the more massive one. This variation also supports our light curve analysis results revealing a semi-detached configuration with the secondary component filling its Roche lobe. Assuming a conservative mass transfer, the mass transfer rate is estimated to be dM/dt = 1.86 10−8 M⊙yr−1. The residuals from the third body and mass transfer approximations also show another cyclic variation of the (O−C) curve, as can be clearly seen in the third panel of Figure 2. The period of this cyclic variation is about 8 yr and the corresponding amplitude in the (O − C) curve is about 0.002 days. Among the existing models proposed to explain cyclic period variations of eclipsing binary stars, two mechanisms have seemed plausible; (i) LITE due to additional objects in the system; (ii) period modulation due to a magnetic activity cycle of the cooler, less massive, secondary star. Based on the analysis of LITE, the minimum mass of the fourth body is estimated to be M4 = 0.13M⊙, which implies that it may be a critical low-mass stellar object. However, in such a case the system will be more unstable. In the case of a magnetic activity effect, we estimated the angular momentum transfer to be ∆J = 1.29·1047 g cm2s−1, required to produce the observed cyclic effect on the orbital period, a required energy ∆E = 5.36·1040 erg for the ∆J transfer, the corresponding luminosity change ∆L = 6.69 1032 erg s−1 and the brightness variation ∆m = 0m.026 of the secondary (active) component. Unfortunately, we do not have enough long-term photometric observations for VX Lac to check such brightness variations. Therefore, we cannot discriminate the responsible mechanism for the cyclic variation in the (O−C) curve at present due to the short time-span of the observational data. Only long-term photometric observations and especially spectroscopic observations will give us a chance to decide on this matter. In our opinion, the cyclic effect with period of about 8 yr on the orbital period change may well be due to a magnetic activity effect of the secondary component.
The positions of the components of VX Lac on the mass-luminosity and mass-radius diagrams in Figure 4 indicate that the primary component is moderately evolved, while the less massive secondary component is above the TAMS line, proving that the primary is under-luminous and the secondary is overluminous, over-sized and evolved. This is a common characteristic seen in Algol type eclipsing binaries (Zola et al. 2016).
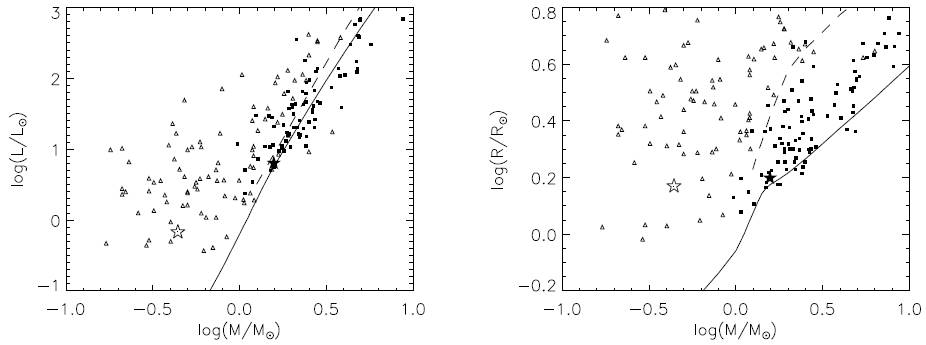
Fig. 4 (Left:) Mass-luminosity relation for both components, (Right:) the mass-radius relation for both components of VX Lac. A solid line represents the ZAMS line and a long dashed line the TAMS line, taken from the theoretical models of Girardi et al. (2000) for solar composition. The filled star indicates the primary component positions of VX Lac, while the open star represents the secondary component. The filled squares represent primaries of semi-detached binaries, while the open triangles indicate the secondaries. Parameters of semi-detached systems are taken from Surkova & Svechnikov (2004).











 nueva página del texto (beta)
nueva página del texto (beta)


