1. BACKGROUND
In 1965 Upgren and Rubin (1965) in an objective-prism study of the distribution in a North Galactic Pole region noted a compact grouping of F-type stars at coordinates RA 12 35 01 and Dec. +36 22 18 (2000). They studied these stars with a one-slit spectrogram on the Cassegrain spectrograph (125Å/mm) of the 36-inch reflector of the Kitt Peak National Observatory. In addition, photoelectric magnitudes and colors in the U, B, V system were determined for five stars with the 28-inch reflector of the Flower and Cook Observatory of the University of Pennsylvania. The separation of the F stars in the sky is about 15 minutes of arc. At a mean distance of 140 parsecs, this separation corresponds to a linear separation of about one parsec. Finally they concluded that the narrow range in the radial velocities and distance modulii for these seven stars suggested that they formed a cluster. If it is assumed that the five dwarf stars define a main sequence, then the turn off was at about spectral class F2, the same point found for the old galactic cluster M 67. They later stated that the apparent great age of the group indicated that a number of fainter stars of low mass, which once belonged to the cluster, may have escaped.
In 1982 Upgren, Philip, & Beavers (1982) in a study through narrow-band photometry with the four-color system and radial velocities stated that these data indicate that five of the seven stars were physically associated and formed a small cluster. The other two stars could also be members. The cluster distance is about 117 pc and its turn off point is near (B − V) = 0.5, which again suggests an age similar to that of the old open cluster M67. They also concluded that it forms the residual core of a much larger cluster, whose fainter members are no longer associated, and is probably in its final stage of dissolution.
In their discussion they stated that Anderson (1966) and Osborn (1967) published proper motions for the stars in an attempt to determine the existence of a mutual association among them. Both concluded that the seven stars do not form a single physical group, although they found that some of them do share a common proper motion.
Upgren et al. (1982) emphasized that if the group were real, it would be a very unusual open cluster. The member stars are very unlikely to be in bound motion around each other. Thus, it is most probable that the group is a residual core of a small open cluster whose fainter and less massive members have had time to dissociate from the loosely bound group.
Later, in 1997, Stefanik et al. (1997) monitored the radial velocities of the seven stars reported by Upgren and Rubin (1965) and determined that two of the stars have velocities which are clearly inconsistent with a physical association with the other five stars.
In 1998 Baumgardt (1998) carried out a study entitled “The nature of some doubtful open clusters as revealed by Hipparcos”, in which the cluster Upgren 1 is included. Based on the parallaxes and proper motions obtained by Gatewood et al. (1988) who concluded that Upgren 1 consists of two dynamically different groups, they collected the parallaxes and proper motions of the 7 stars that could be found in the Hipparcos catalogue. They determined that, with the exception of stars 3 and 5, the proposed members share no common motion and conclude that Upgren 1 is not a cluster.
This result was reinforced later when Baumgardt, Dettbarn & Wielen (2000), in a paper on mem-bership probabilities through proper motions, found that none of the six studied stars belong to a cluster.
There are several reports on uvby − β photo-electric photometry (see Table 1) of the stars originally supposed to belong to Upgren 1; hence, we decided to study this cluster once more using uvby − β photometry, because the question of membership has not been settled. We obtained new uvby − β photoelectric photometry since this system provides a different approach for determining correct distances to each one of the stars (see, for example Peña & Sareyan, 2006). Therefore, the present study could throw fresh light on this matter.
TABLE 1 OBSERVATION OF UPGREN 1 WITH uvby − β PHOTOELECTRIC PHOTOMETRY
| Author | Reference | Number |
|---|---|---|
| Perry (1969) | AJ 74, 705 | 1 star |
| Hilditch, Hill & Barnes (1976) | MRAS 82.95 | 4 stars |
| Upgren, Philip & Beavers (1982) | PASP 94,229 | 7 stars |
| Hill & Barnes (1982) | PDAO XVI 297 | 1 star |
| Olsen (1983) | AAS54,55 | 3 stars |
| Castelaz, Persinger, Stein et al. (1991) | AJ 102, 2103 | 3 stars |
| Olsen(1993) | AAS 102,890 | 1 star |
| Present Paper | 9 stars |
In the compilation of data of open clusters of Paunzen and Mermilliod (2007, WEBDA), no char-acteristics of Upgren 1 have been reported and no membership of the stars to the cluster is provided.
2. OBSERVATIONS
The observations were carried out at the Observatorio Astronómico Nacional (OAN) at San Pedro Mártir, Mexico using a 0.84m telescope with an attached spectrophotometer during six nights in the summer of 2018. On June 1 and June 2 the open cluster was observed. The nomenclature of Rufener (1971) was used to assign IDs to every star, except for a faint star near Star 9 at 2” in the SE direction. We identified this star as Upgren 09b. All are indicated in Figure 1.
2.1. Data Acquisition
The procedure used to acquire the data has been amply utilized in Mexico since the arrival of the “Danish” spectrophotometer in 1986. A description of the typical procedure can be found in Guerrero et al. (2011). What is emphasized here are the numerical values that throw light on the accuracy of the data. The averaged transformation coefficients for each night are listed in Table 2 along with their standard deviations. Season errors were evaluated with the eighteen standard stars observed for a total of 316 observed points. These uncertainties were calculated through the differences in magnitude and colors for all nights, for (V , b − y, m 1, c 1 and β) as (0.028, 0.006, 0.006, 0.014, 0.006) respectively, which provide a numerical evaluation of our uncertainties for the season. Emphasis is made on the large range of the standard stars in magnitude and color values: V :(5.2, 8.8); (b − y):(−0.07, 0.79); m1:(0.10, 0.68); c1:(0.07, 1.12) and β:(2.53, 2.92).
TABLE 2 TRANSFORMATION COEFFICIENTS OBTAINED FOR THE OBSERVED SEASON
| Season | B | D | F | J | H | I | L |
|---|---|---|---|---|---|---|---|
| 2018 | 0.031 | 0.976 | 1.020 | 0.015 | 0.096 | 0.080 | −1.369 |
| σ | 0.038 | 0.011 | 0.027 | 0.015 | 0.046 | 0.081 | 0.124 |
A verification of the goodness of our data was done with the standard stars observed during the season. Transformation coefficients were obtained for each night. With these coefficients, magnitude and colors were obtained for the standard stars. The differences of the obtained values with those of the literature were evaluated for the magnitude and the colors V, (b − y), m 1, c 1 and β.
Once this was done for each night, a compilation of the transformation coefficients was carried out, and mean values and standard deviations were calculated. These are presented in Table 3. In this table Column 1 lists the V value; Columns two to six present the color indexes (b − y), m 1, c 1 and β and the standard deviations. These values are a few hundredths or thousandths of magnitude for each color index providing the accuracy of our photometry. Emphasis must be made on the fact that in total thirty-three uvby measurements (twenty-eight for Hβ) of the standard stars were calculated.
TABLE 3 SEASONAL MAGNITUDE AND COLOR INDEXES DEVIATIONS
| σV | σ(b − y) | σm1 | σc1 | σβ |
|---|---|---|---|---|
| 0.0125 | 0.007 | 0.009 | 0.010 | 0.002 |
Furthermore, to verify the consistency of our de-rived standard stars values, mean values for each star were calculated, as well as their standard deviations. These are presented in Table 4 in increasing brightness. The last Column of this table is, N, the number of entries. In all but HD190849 the standard deviations are on the order of hundredths of magnitude. The large dispersion of this star could be due to variability, as in the case of HD 115520 (Peña et al., 2007).
TABLE 4 STANDARD STARS MEAN PHOTOMETRIC VALUES AND STANDARD DEVIATIONS
| ID | V | (b − y) | m 1 | c 1 | β | σV | σ(b − y) | σm 1 | σc 1 | σβ | N |
|---|---|---|---|---|---|---|---|---|---|---|---|
| BS8085 | 5.171 | 0.653 | 0.665 | 0.140 | 2.495 | 0.011 | 0.002 | 0.004 | 0.015 | 0.024 | 5 |
| BS6332 | 5.249 | −0.003 | 0.180 | 1.113 | 2.863 | 0.013 | 0.002 | 0.006 | 0.012 | 0.022 | 5 |
| BS7858 | 5.355 | 0.017 | 0.215 | 1.002 | 2.895 | 0.010 | 0.002 | 0.003 | 0.006 | 0.013 | 4 |
| BS7253 | 5.496 | 0.168 | 0.192 | 0.766 | 2.749 | 0.011 | 0.003 | 0.005 | 0.007 | 0.012 | 5 |
| BS7503 | 5.948 | 0.397 | 0.207 | 0.396 | 2.590 | 0.010 | 0.005 | 0.003 | 0.005 | 0.004 | 3 |
| BS5633 | 6.021 | 0.031 | 0.187 | 1.061 | 2.900 | 0.018 | 0.004 | 0.001 | 0.008 | 0.023 | 5 |
| BS8086 | 6.031 | 0.799 | 0.648 | 0.075 | 2.477 | 0.044 | 0.005 | 0.003 | 0.018 | 0.023 | 5 |
| BS5270 | 6.186 | 0.627 | 0.093 | 0.483 | 2.537 | 0.026 | 0.003 | 0.005 | 0.009 | 0.014 | 4 |
| BS7504 | 6.206 | 0.403 | 0.211 | 0.384 | 2.595 | 0.013 | 0.005 | 0.002 | 0.005 | 0.012 | 4 |
| HD156026 | 6.389 | 0.692 | 0.695 | 0.282 | 2.532 | 0.023 | 0.010 | 0.005 | 0.015 | 0.023 | 4 |
| HD183085 | 6.709 | 0.241 | 0.129 | 0.898 | 2.706 | 0.031 | 0.005 | 0.009 | 0.013 | 0.012 | 4 |
| HD190849 | 7.368 | 0.057 | 0.152 | 1.000 | 2.884 | 0.560 | 0.022 | 0.019 | 0.012 | 0.019 | 4 |
| HD201193 | 7.884 | 0.335 | 0.147 | 0.436 | 2.622 | 0.041 | 0.002 | 0.009 | 0.012 | 0.000 | 2 |
| HD207608 | 8.029 | 0.313 | 0.143 | 0.544 | 2.627 | 0.008 | 0.006 | 0.011 | 0.015 | 0.006 | 2 |
| HD182941 | 8.069 | 0.277 | 0.123 | 1.032 | 2.802 | 0.017 | 0.005 | 0.005 | 0.012 | 0.019 | 4 |
| HD190296 | 8.090 | 0.069 | 0.152 | 1.152 | 2.879 | 0.143 | 0.020 | 0.003 | 0.029 | 0.011 | 4 |
| HD125607 | 8.092 | 0.548 | 0.384 | 0.336 | 2.583 | 0.018 | 0.005 | 0.005 | 0.007 | 0.028 | 5 |
| HD125375 | 8.121 | 0.197 | 0.134 | 0.859 | 2.731 | 0.015 | 0.001 | 0.004 | 0.010 | 0.008 | 3 |
| HD106509 | 8.144 | 0.327 | 0.134 | 0.474 | 2.648 | 0.013 | 0.004 | 0.005 | 0.020 | 0.014 | 4 |
| HD188755 | 8.262 | 0.098 | 0.204 | 1.015 | 2.844 | 0.025 | 0.005 | 0.008 | 0.011 | 0.014 | 3 |
| HD162503 | 8.286 | 0.454 | 0.183 | 0.443 | 2.591 | 0.019 | 0.006 | 0.004 | 0.012 | 0.012 | 6 |
| HD107550 | 8.343 | 0.489 | 0.143 | 0.413 | 2.566 | 0.021 | 0.004 | 0.008 | 0.006 | 0.009 | 5 |
| HD156392 | 8.409 | 0.341 | 0.151 | 0.647 | 2.710 | 0.039 | 0.006 | 0.007 | 0.026 | 0.019 | 5 |
| HD176014 | 8.673 | 0.341 | 0.109 | 0.575 | 2.642 | 0.012 | 0.004 | 0.003 | 0.015 | 0.029 | 4 |
| HD108641 | 8.821 | 0.515 | 0.274 | 0.331 | 2.575 | 0.006 | 0.004 | 0.006 | 0.014 | 0.014 | 5 |
| HD186025 | 8.847 | 0.385 | 0.125 | 0.540 | 2.670 | 0.059 | 0.020 | 0.007 | 0.020 | 0.011 | 4 |
With the average coefficients we transformed our instrumental magnitudes and colors to the standard system. In particular, since there were two measurements for each star of the cluster Upgren 1, mean values were obtained and the standard deviations calculated. All are below the standard deviation limits.
3. COMPILATION OF uvby - β PHOTOELECTRIC PHOTOMETRY
Since Upgren 1 has several measurements in uvby − β photoelectric photometry reported in the literature and listed in Table 4, we decided to combine all measurements into only one averaged, more significant, value. As we can see in Table 4 the uvby coverage is adequate, but the situation is worse for Hβ, with only four sources: Hilditch, Hill, Barnes (1976), 4 stars; Perry, Johnston, Crawford (1982), 1 star; Hill G., Barnes (1982) (1 star and Castelaz, Persinger, Stein et al. (1991), (4 stars). We measured the nine reported stars.
Table 5 compiles all the photometric values of the observed stars for the cluster. In this table, Column 1 reports the ID of the stars as listed by WEBDA (Paunzen & Mermilliod, 2006.), Columns 2 to 5 the Strömgren values V, (b − y), m 1 and c 1, respectively; next, Column N specifies the number of entries on average presented for each point; next column, the β value, and last Nβ, the number of entries for the average of β. Finally, for each star we present the mean value and in the following row, the standard deviation. As we can see, the standard deviation is on the order of a few hundredths of magnitude and the number of entries is always larger than four, except for β which has a smaller number in a few cases.
TABLE 5 uvby − β PHOTOELECTRIC PHOTOMETRY OF THE OPEN CLUSTER UPGREN 1
| ID | Ref | V | (b − y) | m 1 | c 1 | N | β | Nβ |
|---|---|---|---|---|---|---|---|---|
| 1 | 19 | 7.26 | 0.295 | 0.158 | 0.542 | 2 | ||
| 1 | 166 | 7.28 | 0.296 | 0.161 | 0.541 | 3 | 2.648 | 3 |
| 1 | 297 | 2.661 | 7 | |||||
| 1 | 305 | 7.27 | 0.295 | 0.194 | 0.567 | 2 | ||
| 1 | 345 | 7.284 | 0.298 | 0.161 | 0.54 | 1 | ||
| 1 | pp | 7.286 | 0.296 | 0.152 | 0.566 | 2 | 2.668 | 2 |
| 1 | mean | 7.276 | 0.296 | 0.165 | 0.551 | 2.659 | ||
| 1 | std dev | 0.011 | 0.001 | 0.017 | 0.014 | 0.010 | ||
| 2 | 166 | 0.312 | 0.17 | 0.44 | 3 | 2.634 | 3 | |
| 2 | 305 | 8.13 | 0.316 | 0.2 | 0.443 | 2 | ||
| 2 | 345 | 8.114 | 0.325 | 0.154 | 0.455 | 1 | ||
| 2 | 468 | 8.16 | 0.3 | 0.17 | 0.47 | 1 | 2.64 | 1 |
| 2 | pp | 8.118 | 0.314 | 0.156 | 0.493 | 2 | 2.658 | 2 |
| 2 | mean | 8.131 | 0.313 | 0.170 | 0.460 | 2.644 | ||
| 2 | std dev | 0.021 | 0.009 | 0.018 | 0.022 | 0.012 | ||
| 3 | 166 | 8.23 | 0.262 | 0.165 | 0.512 | 3 | 2.679 | 3 |
| 3 | 305 | 8.2 | 0.267 | 0.185 | 0.531 | 2 | ||
| 3 | 345 | 8.215 | 0.271 | 0.155 | 0.514 | 1 | ||
| 3 | pp | 8.223 | 0.270 | 0.147 | 0.554 | 2 | 2.699 | 2 |
| 3 | mean | 8.217 | 0.268 | 0.163 | 0.528 | 2.689 | ||
| 3 | std dev | 0.013 | 0.004 | 0.016 | 0.019 | 0.014 | ||
| 4 | 166 | 8.75 | 0.309 | 0.181 | 0.407 | 3 | 2.639 | 3 |
| 4 | 305 | 8.76 | 0.313 | 0.204 | 0.408 | 2 | ||
| 4 | 468 | 2.65 | 1 | |||||
| 4 | pp | 8.736 | 0.320 | 0.149 | 0.449 | 2 | 2.653 | 2 |
| 4 | mean | 8.749 | 0.314 | 0.178 | 0.421 | 2.647 | ||
| 4 | std dev | 0.012 | 0.005 | 0.028 | 0.024 | 0.007 | ||
| 5 | 305 | 9.09 | 0.291 | 0.172 | 0.427 | 2 | ||
| 5 | 468 | 9.12 | 0.28 | 0.14 | 0.46 | 1 | 2.64 | 1 |
| 5 | 504 | 9.102 | 0.291 | 0.141 | 0.408 | 1 | ||
| 5 | pp | 9.086 | 0.293 | 0.129 | 0.462 | 2 | 2.654 | 2 |
| 5 | mean | 9.099 | 0.289 | 0.146 | 0.439 | 2.647 | ||
| 5 | std dev | 0.015 | 0.006 | 0.018 | 0.026 | 0.010 | ||
| 6 | 305 | 9.86 | 0.332 | 0.12 | 0.38 | 1 | ||
| 6 | 318 | 9.87 | 0.337 | 0.163 | 0.385 | 3 | ||
| 6 | pp | 9.863 | 0.331 | 0.156 | 0.42 | 2 | 2.656 | 2 |
| 6 | mean | 9.864 | 0.333 | 0.146 | 0.395 | 2.656 | ||
| 6 | std dev | 0.005 | 0.003 | 0.023 | 0.022 | |||
| 7 | 305 | 9.35 | 0.364 | 0.187 | 0.443 | 2 | ||
| 7 | 468 | 9.36 | 0.32 | 0.19 | 0.43 | 1 | 2.61 | 1 |
| 7 | pp | 9.323 | 0.344 | 0.148 | 0.475 | 2 | 2.641 | |
| 7 | mean | 9.344 | 0.343 | 0.175 | 0.449 | 2.626 | ||
| 7 | std dev | 0.019 | 0.022 | 0.023 | 0.023 | 0.022 | ||
| 9 | pp | 10.284 | 0.566 | 0.350 | 0.311 | 2 | 2.592 | 2 |
| UPGREN 09b | pp | 11.568 | 0.391 | 0.235 | 0.275 | 2.640 | 2 |
4. METHODOLOGY
Once we were sure of the quality of the uvby − β data set, further analysis was carried out in order to determine the physical characteristics of the stars in the cluster.
The main problem to tackle was, of course, the determination of membership to the cluster. To do this, the distance to each star had to be calculated. To evaluate the reddening we first established to which spectral class the stars belonged, although it was reported that all were late types (late A and F stars) for which there are calibrations (Nissen, 1988). The procedure has been extensively described in Peña & Martínez (2014). In that article, in § 4 the procedure employed utilizing the prescription of Nissen (1988) is amply described. Photoelectrically we corroborated each star’s spectral type through its location in the [m 1] − [c 1] diagram (Figure 2).
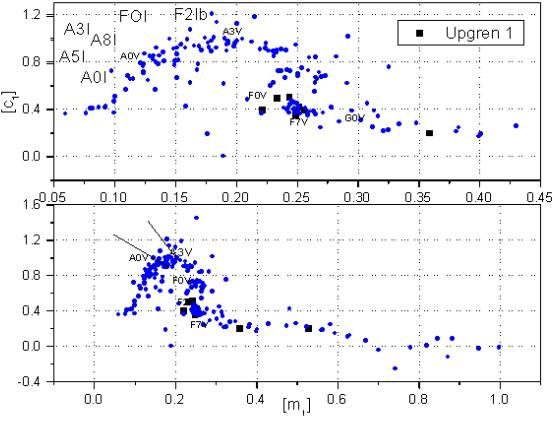
Fig. 2 Position of the stars in the [m1] − [c1] diagram of Alpha Per (Peña & Sareyan, 2006) for Upgren 1. The color figure can be viewed online.
5. RESULTS
Figure 2 shows the position of the stars in the [m 1] − [c 1] diagram for those located in the direction of Upgren 1 on the same diagram of the stars with well-determined spectral types in the open cluster Alpha Per (Peña & Sareyan (2006)).
The application of the above mentioned numerical packages gave the results listed in Table 6 in which the ID, reddening, unreddened indexes, absolute magnitude, DM and distance (in parsecs), are listed. The last two columns present the membership probabilities described below.
TABLE 6 REDDENING AND UNREDDENED PARAMETERS OF THE OPEN CLUSTER UPGREN 1
| Webda | E(b − y) | (b − y) 0 | m0 | c0 | Hβ | V0 | M V | DM | Distance | Membership | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| pp | Upgren (1982) | Stefanik (1997) | ||||||||||
| 3 | .015 | .253 | .168 | .525 | 2.689 | 8.15 | 3.01 | 5.14 | 107 | M | M | M |
| 1 | .009 | .287 | .168 | .549 | 2.659 | 7.24 | 2.09 | 5.15 | 107 | M | N | N |
| 6 | .038 | .295 | .158 | .387 | 2.656 | 9.70 | 3.92 | 5.78 | 143 | M | M | M |
| 4 | .003 | .311 | .179 | .420 | 2.647 | 8.74 | 3.46 | 5.28 | 114 | M | M | M |
| 5 | .000 | .299 | .146 | .439 | 2.647 | 9.10 | 3.23 | 5.87 | 149 | N | M | M |
| 2 | .001 | .312 | .176 | .460 | 2.644 | 8.13 | 2.93 | 5.20 | 110 | M | N | N |
| UPG09b | .038 | .353 | .246 | .267 | 2.640 | 11.41 | 5.27 | 6.13 | 168 | N | ||
| 7 | .008 | .335 | .178 | .447 | 2.626 | 9.31 | 2.80 | 6.51 | 200 | N | M | M |
| 9 | .079 | .487 | .374 | .295 | 2.592 | 9.94 | 4.29 | 5.65 | 135 | M | ||
To establish membership of the stars to the cluster the distance modulus or distance histogram (in pc) were built. The goodness of the method has been tested in the past by comparing our results to the proper motion studies for a well-studied cluster, α Per (Peña & Sareyan, 2006). In this paper the intersection of our data set with the Strömgren photometry of Crawford & Barnes (1974) plus the photometry from Mitchell (1960) constituted 45 entries. The results were compared with the work of Heckmann et al. (1956) and the agreement was remarkable: Sixty stars coincide in membership. In that paper we wrote that given the previous num-bers, we can draw the following conclusions: out of 75 stars in the membership interval, 53 are assumed to be members by HDK and there is disagreement on three. Considering the results of Prosser (19932) the matching is more than adequate. Out of 75 stars which we have defined as member stars, only three are non-members according to Prosser (1992), al-though two were established as members by Heckmann et al. (1956). A final comparison of membership was done with the data of the Hipparcos and Tycho catalogues proper motions. Among the sample of stars we observed, 58 had measurements in these catalogues. Only a few stars in the catalogues did not belong to the uvby data sample. Assuming membership for those stars within the one sigma criterion, the coincidences were remarkable: only three of the stars that we supposed to be non-members could be members according to the Hipparcos results. For the stars that we considered to be members, only seven were not assigned cluster membership according to the Hipparcos measurements. On the other hand, 33 stars that Hipparcos measurements consider members were also clearly members according to our analysis. In view of the previously reported results on Alpha Per compared with the cannonical membership methods, we conclude that determining membership by the uvby − β calibration technique provides reliable results.
When the histogram of distance for Upgren 1 was built (Figure 3), the distances of the stars showed a clear accumulation at a distance of (123 ± 17) pc; the peak was determined by a Gaussian fit to the distribution.
To determine membership to the cluster we established a numerical criterion that to be a member of the cluster, the distance to the star should be within one sigma of the mean average distance. For the accumulation of stars, membership of each one is indicated by M in the twelfth Column of Table 6. Those outside of the membership limits are denoted by N, non-member. We have compared our memberships with those reported in WEBDA for Upgren 1. The membership probabilities reported are listed in the last Column of Table 6. In the previous column the photometric membership is also presented.
The effective temperature of the hottest stars was fixed by plotting the location of all stars on the theoretical grids of Lester, Gray & Kurucz (hereinafter LGK86), after calculating the unreddened colors (Figure 4) for the correct chemical composition of the considered model. The metallicity of Upgren 1 was not reported by WEBDA, but it is calculated in this work. Discarding the high value of Star 9, a [Fe/H] value of 0.039 ± 0.08 is obtained.
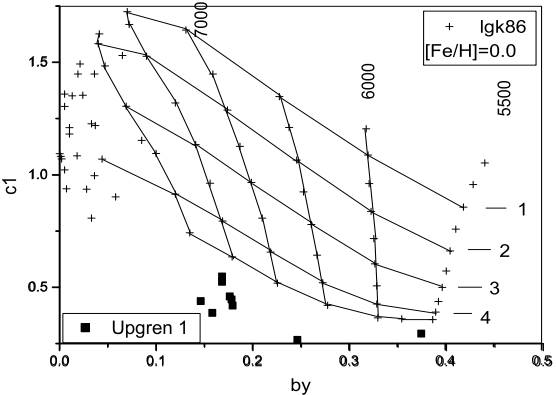
Fig. 4 Location of the unreddened points (filled squares) in the LGK86 grids. Values of effective temperature and surface gravity are indicated. X axis presents (b − y)0, axis is c 0
Once the membership and effective temperature are established for the hottest star, its age is determined through the calibrations of Meynet, Mermilliod & Maeder (1993). For the cool stars of this cluster the valid relation is given by a log age of 15.142(log Te)2 − 122.810(log Te) + 257.518 valid in the range of log T e[3.79; 3.98). For the hottest star, Star 6, it gives a log age of 8.85.
The obtained results are compared to those previously known in Table 7.
TABLE 7 NEWLY DETERMINED CHARACTERISTICS OF THE OPEN CLUSTER UPGREN 1
| ID | Upgren (1982) | PP |
|---|---|---|
| Distance [pc] | 120 ± 10 pc | 119 ± 16 pc |
| Reddening [mag]E(b-y) | 0.0 | 0.024 ± 0.030 |
| Distance modulus [mag] | 5.39 ± 0.18 | 5.3 ± 0.3 |
| Log age | 9.5 | 8.85 |
| [Fe/H] | − | 0.04 ± 0.08 |
6. DISCUSSION
Membership was assigned for those stars within one sigma of the mean value. Five stars were considered to be members in this fashion and three to be non-members.
Upgren et al (1982) concluded that Stars 3, 4, 5, 6, and 7 are associated, since the radial velocities, photometry, and spectral classifications are all concordant and the proper motions for 4 and 6 are not grossly different from those of the other three stars. Star no. 1 is not likely to be a member based on its radial velocity and its proper motion. Star no. 2 is a possible but unlikely member, since it too has a radial velocity in disagreement with the other stars. The distance modulus of the group determined from the five most probable stars alone is close to that given above based on all seven stars; it is 5.34 ± 0.25 which leads to a distance of 117 ± 13 pc.
Our findings are somewhat discordant with those of Stefanik et al. (1997) who determined that the radial velocity data indicated that five Stars (3, 4, 5, 6, and 7) had very similar radial velocities and could be kinematically associated, whereas the radial velocities of Stars 1 and 2 indicated no association with the other five. They stated that the proper motions and trigonometric parallaxes of Stars 3 and 6 may not be reliable, because of the multiple nature of these systems.
In their concluding remarks Upgren et al (1982) stated that: “Unlike any other star-poor cluster, Upgren 1 is old, and is perhaps unique among all known clusters for this reason. Its probable uniqueness suggests that it is being observed just prior to its final dissolution and that this stage is a relatively short one”. However, in another cluster under investigation (Dzim 5) we have found (Peña et al. 2018) that it has analogous characteristics, and we concluded that Dzim 5, according to us and to WEBDA, might or not be a cluster. Our findings are puzzling. There is a small group of five or six stars, basically at the same distance, but all of late spectral type. There is no indication of early type stars present or past. Nevertheless, our results are uncontroversial.
7. CONCLUSIONS
The main problem we tackled remains. From uvby − β photoelectric photometry determined from the average of all existing measurements, we derived reddening and distances to each star. We assigned membership from the coarse average of all of them. Our memberships agree with those determined by Upgren, Philip and Beaver (1982) from radial velocities, photometry, and spectral classifications for three of the stars and disagree for another three. There is agreement with some Stars (3, 4 6) that seem to conform a physical group; three more (1, 2, 5) have contradictory results. The WEBDA membership, on the other hand, assigns zero probability of membership to the cluster for all the stars.
The location of the stars in the theoretical grids of Lester, Gray and Kurucz (1986) shows values of log g higher than 4.5, implying compact objects. The temperatures lie around 7500 K to 8000 K, concor-dant with their spectral types.
At any rate, different studies with radically different techniques find that there is a physical attached group of stars.











 nueva página del texto (beta)
nueva página del texto (beta)




