1.Introduction
Since the discovery of the first planet orbiting another star in the 1990s, the number of confirmed exoplanets had steadily increased reaching in November of last year 4133.1 The urgent tasks with which we are faced now are determining the compositions of these exoplanets and understanding how they formed. However, although that should have been straightforward (Seager 2010), the detection of new types of planets had complicated the matter, changing in a crucial way our understanding of the formation of planetary systems around stars like the Sun.
The first new type of planets to be discovered was the “hot Jupiters” (HJs; Mayor & Queloz 1995), which are gas giants like Jupiter and Saturn, but with extremely small periods, , consistent with semi-major axes smaller than . The existence of HJs is problematic because, according to the model of formation of the solar system, they can only form in the protoplanetary disk (PPD) where it is cold enough for volatile compounds such as water, ammonia, methane, carbon dioxide and monoxide to condense into solid ice grains (Plummer et al. 2005). In the Solar System, this happens beyond the ice-line, which is located close to 3 AU (Martin & Livio 2012). This implies that HJs must have formed farther out in the cold regions of the PPD, then migrated close to their stars (Lin et al. 1996). Subsequent discoveries have then shown that far from being exceptional, artifacts of an observational bias, HJs turned out to be very common around Sun-like stars, suggesting that large scale migration is a standard feature of the planet formation process (Butler et al. 2000; Udry & Santos 2007).
Two other new types of planets discovered are the “Super-Earths” (Leconte et al. 2009; Valencia et al. 2006; Martin & Livio 2015; Chabrier et al. 2009) and the “mini-Neptunes” (Gandolfi et al. 2017). These too were found to be common and very close to their stars, which, consequently, also makes them “hot”. Their discoveries are important for two reasons. The first reason is that it makes the alternative “in situ” model for the formation of HJs (e.g., Boss 1997) a special model, since it cannot explain the large mass range and diversity of the “hot” exoplanets observed (Super-Earths and mini-Neptunes in situ models are discussed in Raymond et al. 2008; Chiang & Laughlin 2013). The second reason is that it was recently established by Lee et al. (2017) that their numbers around their host stars fall rapidly for periods P < 10 days (≈0.09 AU), which, assuming Keplerian orbits, clearly implies they all formed farther out (beyond 0.1 AU) and have migrated inward, but with a good many disappearing into their stars. This, once again, puts large scale migration at the front scene of the planet formation process.
This brings us to the present fundamental question in planet formation theory (McBride & Gilmour 2004): what explains the fact that large scale migration did not happen in the Solar System? Or, in other words, assuming all planets form in a PPD around a low mass star (Nomura et al. 2016; van der Marel et al. 2018; Pérez et al. 2019), what difference would make migration more important in one case and less important in another (see discussion in Walsh et al. 2011)?
Integrating the migration process into a consistent model of planet formation is an extremely active and fast evolving field of research (a recent review of this important subject can be found in Raymond & Morbidelli 2020). In the case of the HJs, two migration mechanisms are accepted now as most probable (Dawson & Johnson 2018): (1) disk migration, where the planet forms beyond the ice-line and then migrates inward by loosing its orbit angular momentum to the PPD (see thorough reviews in Baruteau et al. 2014; Armitage 2020), and (2) high-eccentricity migration, according to which the planet first gains a high eccentricity through interactions with other planets, which makes it to pass very close to its star, where it looses its orbit angular momentum by tidal interactions (this is a more complicated process, involving different mechanisms; e.g., Rasio &. Ford 1996; Weidenschilling & Marzari 1996; Marzari & Weidenschilling 2002; Chatterjee et al. 2008; Nagasawa et al. 2008; Beaugé & Nesvorný 2012). However, what is not clear in these two models is, what importance must be put on the characteristics of the PPD, its mass, size, depth and composition?
According to PPD formation theory, there are two possible mass scenarios (Armitage 2020): the minimum mass model, between 0.01 to 0.02
In terms of angular momentum, the differences between the minimum and maximum mass model for the PPD might also be important. By definition, the angular momentum of a planet is given by the relation :
where Mp and M* are the masses of the planet and its host star, αp is the semi-major axis of the planet and ep its eccentricity. This suggests that within the maximum mass model more massive planets would also be expected to have higher orbital angular momentum (through their PPD) and, consequently, to have lost a larger amount of their angular momentum during large scale migration (
In the case of the planets, the two most successful detection techniques, the radial velocity (RV) and transit (Tr) methods, yield estimates of the mass of a planet, Mp, and its radius, Rp, as well as the semi-major axis, αp, and the eccentricity of its orbit, ep. The first two parameters constrain their composition and formation process in the PPD, while the last two give information about their migration. By combining the four parameters we can also retrieve the angular momentum of the orbits of the planets (cf. equation 1). In the case of the stars the most important characteristics that can be derived from their spectra are the effective temperature, Teff, the surface gravity, log g, the metallicities, [M/H] or [Fe/H], and the rotational velocity, Vsini. The first two can be used in combination with their magnitudes and distances (using GAIA parallaxes) to determine their radii and masses which, taken in combination with the rotational velocity, yield the angular momentum (or spin) of the star, J*:
where M*, R* and γ* are the star mass, radius and moment of inertia (which depends on the mass of the star; cf. Irwin 2015), and
To understand how the formation of planets is connected with the formation of their host stars, we must, consequently, make an effort to determine in parallel with the discovery of the former the physical characteristics of the latter. Present data banks for exoplanets (e.g., Kepler and now TESS, with 51 confirmed discoveries, and future surveys like PLATO)2 require follow-up observations and analysis for the host stars, which are usually done with large diameter telescopes equipped with high resolution spectrographs. However, for the brightest stars (TESS targets, for example, being 30-100 times brighter than KEPLER stars), the use of smaller diameter telescopes equipped with lower resolution spectrographs might be more efficient in acquiring the information. Moreover, although high resolution spectra is justified when one uses the standard spectral analysis method, which is based on modeling the equivalent width (EW) of spectral lines, this might not be necessary when one uses the synthetic spectral analysis (e.g., Valenti & Debra 2005), which consists in fitting observed spectra to grids of synthetic spectra with well determined physical characteristics that can be produced at different spectral resolutions. Another problem in using large aperture telescopes for host stars follow-up is that, since these telescopes are in high demand (for faint objects), data are collected on short duration runs by different groups using different techniques and codes (although the same analysis method), which introduces discrepancies between the results (Hinkel et al. 2014, 2016; Blanco-Cuaresma 2014; Jófre et al. 2017). This suggests that a follow-up using a dedicated telescope and applying only one method of analysis could produce more homegeneous data (one effort to homogenize data is the Stars With ExoplanETs CATalog or SWEET-Cat for short; Sousa et al. 2008). For these reasons we developed a new method based on stellar spectral analysis for data obtained with the TIGRE telescope (Telescopio Internacional de Guanajuato Robótico Espectroscópico) that is installed at our institution in Guanajuato.
TIGRE is a 1.2 m fully robotic telescope located at the La Luz Observatory (in central Mexico) at an altitude of 2,400 m; a more detailed description can be found in Schmitt et al. (2014). Its principal instrument is the fibre-fed echelle spectrograph HEROS (Heidelberg Extended Range Optical Spectrograph), which yields a spectral resolution R ≈ 20,000, covering a spectral range from 3800 Å to 8800 Å. The queue observing mode and automatic reduction pipeline already implemented for this telescope allow to optimize the observation and reduction process, producing highly homogeneous data rapidly and confidently. To optimize the analysis process, we developed a semi-automatic method that allows us to derive efficiently the most important physical characteristics of the stars: Teff, log𝑔, [M/H], [Fe/H], and 𝑉sin𝑖. This was done by applying the synthetic spectral fitting technique as offered by the code iSpec (Blanco-Cuaresma 2014), which was shown to yield results that are comparable to results in the literature obtained through different methods and codes (Blanco-Cuaresma 2019).
The goal of this first article is to explain our spectral analysis method based on iSpec and to compare results obtained by TIGRE with data taken from the literature. In an accompanying paper (Flor-Torres et al., hereinafter Paper II) we will present a preliminary study, based on our own observational results, about the coupling of the angular momentum of the exoplanets and their host stars.
2. Sample of host stars with exoplanets observed with TIGRE
Our initial target list for a pilot project was built from the revised compendium of confirmed exoplanets in the Exoplanet Orbit Database (hereinafter Exoplanets.org,3) selecting all stars with spectral types F, G or K, located on the main sequence (based on their luminosities and colors), and for which a confirmed planet with well determined mass, radius, and semi-major axis was reported. Note that we did not apply a restriction to single systems, since from the point of view of the angular momentum we verified that only the major planet of a system counts (like Jupiter in our solar system). To optimize our observation with TIGRE, we restricted further our target list by retaining only host stars that have a magnitude V ≤ 10.5, obtaining a much shorter list of 65 targets.
Our observed sample consists of 46 stars, hosts of 59 exoplanets, which were observed by TIGRE in queue mode. In Table 1 the stars observed are given a running number (Column 1) which is used to identify them in the different graphics. The V magnitude of each star and its distance as calculated from Gaia parallaxes are listed in Columns 3 and 4 respectively. Also shown are the exposure times, in Column 5, and the signal to noise ratio (S/N) in Column 6, as measured in the red part of the spectrum. The last column lists the main references found in the literature with data about the host stars and their planetary systems.
Table 1 Stars observed with the TIGRE
| Id. # | Star | Magnitude (V) | Distance (pc) | Exp. time (min) | S/N | Ref. (as found in exoplanets.org) |
|---|---|---|---|---|---|---|
| 1 | *KELT-6 | 10.3 | 242.4 | 97.1 | 54 | Damasso et al. (2015) |
| 2 | *HD 219134 | 5.6 | 6.5 | 8.0 | 139 | Motalebi et al. (2015) |
| 3 | *KEPLER-37 | 9.8 | 64.0 | 93.2 | 75 | Batalha et al. (2013) |
| 4 | HD 46375 | 7.8 | 29.6 | 108.0 | 107 | Marcy et al. (2000) |
| 5 | HD 75289 | 6.4 | 29.1 | 37.8 | 99 | Udry et al. (2000) |
| 6 | HD 88133 | 8.0 | 73.8 | 116.0 | 94 | Fischer et al. (2005) |
| 7 | HD 149143 | 7.9 | 73.4 | 108.0 | 93 | Fischer et al. (2006); da Silva et al. (2006) |
| 8 | HAT-P-30 | 10.4 | 215.3 | 100.9 | 59 | Johnson et al. (2011) |
| 9 | KELT-3 | 9.8 | 211.3 | 92.5 | 68 | Pepper et al. (2013) |
| 10 | KEPLER-21 | 8.3 | 108.9 | 29.4 | 83 | Borucki et al. (2011) |
| 11 | KELT-2A | 8.7 | 134.6 | 54.3 | 95 | Beatty et al. (2012) |
| 12 | HD86081 | 8.7 | 104.2 | 61.4 | 100 | Johnson et al. (2006) |
| 13 | WASP-74 | 9.8 | 149.8 | 96.5 | 73 | Hellier et al. (2015) |
| 14 | HD 149026 | 8.1 | 76.0 | 37.4 | 98 | Sato et al. (2005) |
| 15 | HD 209458 | 7.6 | 48.4 | 40.0 | 98 | Henry et al. (2000); Charbonneau et al. (2000) |
| 16 | BD-10 3166 | 10.0 | 84.6 | 100.8 | 72 | Butler et al. (2000) |
| 17 | HD 189733 | 7.6 | 19.8 | 33.1 | 102 | Bouchy et al. (2005) |
| 18 | HD 97658 | 7.7 | 21.6 | 35.0 | 123 | Howard et al. (2011) |
| 19 | HAT-P-7 | 10.5 | 344.5 | 43.5 | 32 | Pál et al. (2008) |
| 20 | KELT-7 | 8.5 | 137.2 | 47.2 | 93 | Bieryla et al. (2015) |
| 21 | HAT-P-14 | 10.0 | 224.1 | 84.0 | 57 | Torres et al. (2010) |
| 22 | WASP-14 | 9.7 | 162.8 | 74.6 | 66 | Joshi et al. (2009) |
| 23 | HAT-P-2 | 8.7 | 128.2 | 70.0 | 69 | Bakos et al. (2007) |
| 24 | WASP-38 | 9.4 | 136.8 | 75.8 | 82 | Barros et al. (2011) |
| 25 | HD 118203 | 8.1 | 92.5 | 41.5 | 92 | da Silva et al. (2006) |
| 26 | HD 2638 | 9.4 | 55.0 | 104.6 | 82 | Moutou et al. (2005) |
| 27 | WASP-13 | 10.4 | 229.0 | 123.7 | 51 | Skillen et al. (2009) |
| 28 | WASP-34 | 10.3 | 132.6 | 136.8 | 62 | Smalley et al. (2011) |
| 29 | WASP-82 | 10.1 | 277.8 | 98.1 | 51 | West et al. (2016) |
| 30 | HD17156 | 8.2 | 78.3 | 46.3 | 98 | Fischer et al. (2007) |
| 31 | XO-3 | 9.9 | 214.3 | 70.8 | 60 | Johns-Krull et al. (2008) |
| 32 | HD 33283 | 8.0 | 90.1 | 53.4 | 101 | Johnson et al. (2006) |
| 33 | HD 217014 | 5.5 | 15.5 | 40.0 | 254 | Mayor & Queloz (1995) |
| 34 | HD 115383 | 5.2 | 17.5 | 4.0 | 105 | Kuzuhara et al. (2013) |
| 35 | HAT-P-6 | 10.5 | 277.5 | 125.0 | 49 | Noyes et al. (2008) |
| 36 | *HD 75732 | 6.0 | 12.6 | 28.7 | 141 | Marcy et al. (2002) |
| 37 | HD 120136 | 4.5 | 15.7 | 9.3 | 174 | Butler et al. (2000) |
| 38 | WASP-76 | 9.5 | 195.3 | 91.1 | 73 | West et al. (2016) |
| 39 | Hn-Peg | 6.0 | 18.1 | 8.0 | 99 | Luhman et al. (2007) |
| 40 | WASP-8 | 9.9 | 90.2 | 150.0 | 81 | Queloz et al. (2010) |
| 41 | WASP-69 | 9.9 | 50.0 | 90.0 | 76 | Anderson et al. (2014) |
| 42 | HAT-P-34 | 10.4 | 251.1 | 105.0 | 56 | Bakos et al. (2012) |
| 43 | HAT-P-1 | 9.9 | 159.7 | 75.0 | 60 | Bakos et al. (2007) |
| 44 | WASP-94 A | 10.1 | 212.5 | 105.0 | 58 | Neveu-VanMalle et al. (2014) |
| 45 | WASP-111 | 10.3 | 300.5 | 90.0 | 58 | Anderson et al. (2014) |
| 46 | HAT-P-8 | 10.4 | 212.8 | 150.0 | 74 | Latham et al. (2009) |
An * in front of the name of the star identifies multiple planetary systems
The HEROS spectrograph on TIGRE is coupled to two ANDOR CCDs, cooled by thermocouple (Peltier cooling to -100 C): blue iKon-L camera DZ936N-BBB and red iKon-L camera DZ936N-BV. This yields for each star two spectra, one in the blue, covering a spectral range from 3800 Å to 5750 Å, and one in the red, covering a spectral range from 5850 Å to 8750 Å. All the data were automatically reduced by the TIGRE/HEROS standard pipeline, which applies automatically all the necessary steps to extract Echelle spectra (Hempelmann et al. 2016; Mittag et al. 2016): bias subtraction, flat fielding, cosmic ray correction, order definition and extraction and wavelength calibration, which was carried out by means of Th-Ar lamp spectra taken at the beginning and end of each night. Finally, we applied a barycentric correction and as a final reduction step, corrected each spectrum for telluric lines using the code developed by Smette et al. (2015). After verification of the results of the reduction process, we decided to concentrate our spectral analysis only on the red part of the spectra, where the S/N is higher.
In Figure 1 we show the S/N obtained as a function of the exposure time. For each star the total exposure time during observation was adjusted to reach S/N ≥ 60. Note that this result only depends on the telescope diameter, the fiber transmission, the spectrograph resolution (we used R = 20,000, but the resolution is adjustable in iSpec) and the photometric conditions (explaining most of the variance).The average exposure time was 74 s for an average S/N ≈ 87 , which makes observation with a very efficient process.
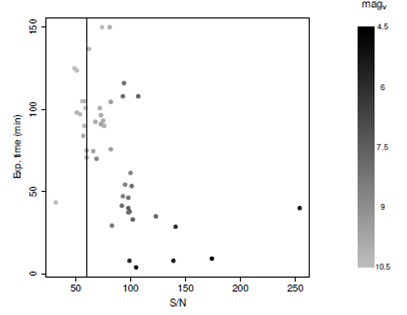
Fig. 1 S/N as a function of exposure time for our sample, limited to stars with magnitude limit V≤ 10.5. Note that the exposure time was adjusted to reach S/N ≥ 60 in less than two hours.
To determine how faint a follow-up with TIGRE could be done efficiently, we traced in Figure 2 an exponential growth curve based on our data, determining the S/N expected in one hour for stars with different magnitudes. One can see that a star with 10.5 mag in V would be expected to have a S/N near 30 (or 60 in 2 hours). The lowest we could go would be S/N ≈10 which would be reached in one hour for a 12.5 mag star (or 2 hours for a 13 mag star). Since it is not clear how low the S/N of a star could be to be efficiently analysed using the synthetic-spectra method, we judged safer to adopt a limit S/N of 60, which can be reached within two hours using TIGRE. This justifies the magnitude limit, V ≤ 10.5, adopted for this pilot project. Our observations suggest that a 1.2 m telescope could contribute significantly to the follow-up of exoplanet surveys like TESS, searching for small rocky planets around bright stars (stars much brighter than stars), and in the near future PLATO, which will search for Earth-like planets in the habitable zones of one million nearby Solar type stars.
3. Spectral analysis using iSpec
Our spectral analysis was developed using the synthetic spectral fitting technique offered by the code iSpec (version 2016.11.18; Blanco-Cuaresma 2014, 2019). In brief, this technique consists in comparing an observed spectrum with synthetic spectra interpolated from pre-computed grids, calculated using different radiative transfer codes, and applying a least-squares minimization algorithm to converge towards the closest approximation possible. In Figure 3 we show one example of a synthetic spectral fit for the star HD 46375. The fit has a rms 0.0319, which is relatively good considering HEROS intermediate resolution (Piskunov & Valenti 2017). Due to the low resolution of our spectra we can fit at the same time in a homogeneous manner the intensity and spectral profiles of more than 100 lines (compared to a few 10s at high resolution; e.g., Valenti & Debra 2005). The best fit then allows to determine five important atmospheric parameters: i.e., the effective temperature, Teff, the surface gravity, logg, two indexes of metallicities, [M/H] and [Fe/H], and the rotational velocity, Vsini.
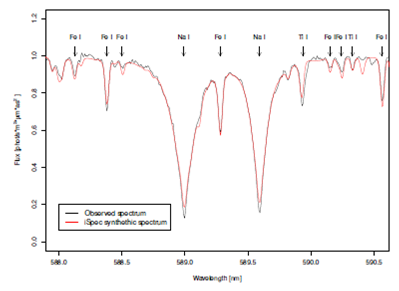
Fig. 3 Example of the result for the synthetic spectral fitting method in iSpec. The star is HD 46375, the observed spectrum is shown in blue and the fitted spectrum in red, with a rms of 0.0319. The color figure can be viewed online.
To optimize our analysis a crucial step of our method consisted in applying iSpec to a TIGRE spectrum from the Sun (as reflected by the Moon). Our main goal was to determine a subset of spectral lines and segments that best reproduced the physical characteristics of our star. Although this step is time consuming because each line and segment has to be tested incrementally by running iSpec, once these lines and segments are established, the analysis of stars becomes straightforward and efficient, the full process taking only a few minutes to converge on a modern desktop computer. Starting with the whole line-list available in the VALD database (Kupka et al. 1999, 2011), we kept only 122 lines in the red for which we defined specific segments in Table 1 of Appendix A. As we already verified in Eisner et al. (2020), these lines and segments can also be used in iSpec as a standard basis for observations obtained with different telescopes and (once adjusted for the resolution) other spectrographs.
Our initial analysis of the Sun also allowed us to decide which solar abundance, atmospheric model and radiative transfer code were optimal. We adopted the solar abundance of Asplund et al. (2009), the ATLAS atmospheric model of and the radiative transfer code SPECTRUM of . Another parameter that turned out to be important using iSpec is a correction for limb darkening, which we fixed to a value of 0.6 (Hestroffer & Magnan 1998; Blanco-Cuaresma 2019).
After working out the analysis of the Sun, we found an unexpected difficulty in obtaining the rotation velocity, Vsini, for our stars. The problem comes from the fact that in low mass stars the turbulence velocity Vmic and Vmac have values comparable to Vsini (Doyle et al. 2014), and there is consequently no fail-proof recipe how to “constrain” these velocities using the synthetic method. One way to approach this problem (following different researchers in the field) is to adopt ad hoc values based on theory or observation (Gray 1984a,b; Fischer & Valenti 2005; Bruntt et al. 2010; Tsantaki et al. 2014; Doyle et al. 2014). For our analysis, we decided to adopt empirical values. For Vmac we used the relation (Doyle et al. 2014):
where ΔT=(Teff - 5777), α = 3.21, b = 2.33 x 10-3 and c = 2.00 x 10-6. For Vmic we used the relation (Tsantaki et al. 2014):
Note that neither authors give uncertainties on these values. However, suggest generic uncertainties of the order of ± 0.27 km/s and ± 0.15 for Vmac and Vmic respectively, which we adopted for our study.
In Figure 4 we show the final values of Vmac obtained in our analysis. Traced over the data, we draw the different relations proposed in the literature to fix this parameter. At high temperatures (Teff > 5800 K), one can see that our values for 𝑉 𝑚𝑎𝑐 are well above the upper limit determined by Valenti & Fischer (2005), while at low temperatures, the values are well above the lower limit determined by Bruntt et al. (2010). In general, our results for Vmac are consistent with the values expected based on the relation proposed by Gray (1984b).
Our final result for the Sun is shown in Table 2. These values were obtained after only ten iterations, using the parameters of the Sun as initial guess and fixing Vmac and Vmic using equation 3 and equation 4. For comparison, we also included in Table 2 the values adopted for the Gaia Benchmark stars. Although our best fit reproduces well the physical characteristics of the Sun, the uncertainty estimated by for 𝑉sin𝑖 is relatively high. But this, as we already explained, is expected considering the problem related to Vmic and Vmac. The different solutions (as shown in Figure 4) to this problem might explain, for example, why the macro turbulence we used for the Sun is lower than what was used by Gaia. In Doyle et al. (2014), the authors already noted a similar difference, by comparing the values they obtained by their relation with results reported by Fischer & Valenti (2005), where the Vmac were systematically higher by as much as 0.54km s-1. However, adding this difference (as a systematic correction) to bring our result for Vmac closer to the value proposed in the Gaia Benchmark, did not lower the uncertainties on Vsini obtained with iSpec. Therefore, considering that our method easily reproduces the value of Vsini for the Sun, we judged more realistic to keep a high uncertainty on this parameter. Besides, the question is possibly more complex, considering the uncertainty on the existence of a J - M relation,
Table 2 Results for the solar spectrum using ISPEC
| Char. | iSpec | Sun* |
| Teff | 5571 ± 30 K | 5571 K |
| log g | 4:44 ± 0:04 dex | 4:44 dex |
| [M/H] | 0:00 ± 0:03 | 0 |
| [Fe/H] | 0:00 ± 0:03 | 0 |
| V sin i | 1:60 ± 1:45 km/s | 1:60 km/s |
| Vmic | 1:02 km/s | 1:07 km/s |
| Vmac | 3:19 km/s | 4:21 km/s |
| Rms of fit | 0:0289 |
*Gaia benchmark Stars values(Blanco-Cuaresma 2019).
For the analysis of the stars, our semi-automatic method can be summarized in the following way. We first run iSpec using the parameters of the Sun as initial input. This implies calculating Vmac and Vmic using equation 3 and equation 4, keeping these values fixed and leaving all the other parameters free. The results of the first run give us new values of Teff and logg based on which we calculate new initial values for Vmac and Vmic before running iSpec a second time.
To verify our solutions, for each star we use the final value of Teff to calculate its mass and radius (first we get the mass, then the corresponding radius) using the mass-luminosity relation for stars with masses between 0.43
where L is the bolometric luminosity as determined from its magnitude in V and its distance calculated from Gaia in Table 1. Then, we verify that the value of logg given by iSpec is consistent with the mass and radius obtained using the relation (equation 7 in Valenti & Debra 2005):
In general, we obtained consistent values for logg, within the generic errors suggested by Doyle et al. (2014). However, for eight stars, we found discrepant masses, the masses obtained using equation 6 being higher than the masses using equation 5. To solve this problem we found it important to better constrain the initial value of
4.Results: characterization of the host stars of exoplanets observed with TIGRE
Our measurements for the physical parameters of the host stars as determined with our semi-automatic method are presented in Table 3. Note that for the metallicities, [M/H] and [Fe/H], an extra correction was needed following Valenti & Debra (2005), to eliminate spurious abundance trends (see their explanations in § 6.4). This correction is based on the assumption that the ratio of one elemental abundance to another must not vary systematically with the temperature. The correction then is simple: it consists in tracing the metallicities as a function of Teff, fitting a second order relation, then subtracting this spurious relation from the data. All the uncertainties reported in Table 3 were calculated by , while the errors of the radii and masses are the quadratic sums of the uncertainties of the parameters used to calculate these values (see § 7.2 in Valenti & Debra 2005). As explained Valenti & Debra (2005) and in Piskunov & Valenti (2017) the uncertainties estimated by the algorithms that produce the synthetic spectra and fit them to the observed spectra are usually undetermined, as compared to the random errors calculated from the measurements of multiple observations of the stars (§ 6.3 in Valenti & Debra 2005). Unfortunately, multiple observations were not programmed for our stars and we have only 4 stars in our study (17, 19, 23 and 46) that were observed more than once (four times for three and six times for the fourth one). This means that only a rough estimate of the random error can be obtained for our pilot-survey by calculating for each of these stars the standard deviations of the parameters measured applying the same spectral analysis as for the other stars. In table 4 we compare our mean uncertainties as obtained with iSpec the mean of the standard deviations for the multiply observed stars in our sample. Except for 𝑉sin𝑖, the mean empirical errors are much larger than the iSpec values. In particular, our empirical errors are larger than the empirical uncertainties calculated by Valenti & Debra (Figure 9 in 2005), being comparable to their 2 sigma probabilities (the values in the table correspond to 1 sigma, the threshold that includes 68.3% of their error measurements).
Table 3 Physical parameters of the host stars of exoplanets in our sample, as determined with ISPEC
| No | Name o star | Teff (K) | ∆Teff (k) | log g | ∆log g | [M/H] | ∆[M/H] | [Fe/H] | ∆[Fe/H] | V sin i | ∆V sin i | Vmic | Vmac | rms | R* |
∆R* |
M* |
∆M* |
| 1 | KELT-6 | 6176 | 24 | 4.03 | 0.05 | −0.38 | 0.02 | −0.14 | 0.03 | 6.52 | 0.82 | 1.44 | 5.28 | 0.0292 | 1.71 | 0.20 | 1.22 | 0.20 |
| 2 | HD 219134 | 5209 | 13 | 4.90 | 0.00 | 0.00 | 0.02 | 0.02 | 0.01 | 7.09 | 0.30 | 0.47 | 1.61 | 0.0318 | 0.54 | 0.09 | 0.77 | 0.09 |
| 3 | KEPLER-37 | 5520 | 19 | 4.50 | 0.04 | −0.40 | 0.02 | −0.28 | 0.02 | 6.62 | 0.50 | 0.82 | 2.62 | 0.0317 | 0.71 | 0.15 | 0.88 | 0.15 |
| 4 | HD 46375 | 5345 | 22 | 4.47 | 0.04 | −0.05 | 0.01 | 0.11 | 0.01 | 2.01 | 0.73 | 0.71 | 2.52 | 0.0319 | 0.83 | 0.01 | 0.88 | 0.02 |
| 5 | HD 75289 | 6196 | 23 | 4.16 | 0.06 | 0.16 | 0.02 | 0.42 | 0.02 | 4.11 | 0.56 | 1.41 | 5.10 | 0.0291 | 1.27 | 0.01 | 1.14 | 0.03 |
| 6 | HD 88133 | 5582 | 16 | 4.05 | 0.03 | 0.15 | 0.01 | 0.34 | 0.01 | 1.98 | 0.76 | 1.02 | 3.61 | 0.0344 | 1.80 | 0.01 | 1.12 | 0.02 |
| 7 | HD 149143 | 6067 | 20 | 4.36 | 0.04 | 0.17 | 0.02 | 0.48 | 0.02 | 3.53 | 0.61 | 1.25 | 4.22 | 0.0316 | 1.64 | 0.10 | 1.19 | 0.10 |
| 8 | HAT-P-30 | 6177 | 30 | 3.81 | 0.08 | 0.06 | 0.04 | 0.15 | 0.03 | 8.88 | 0.60 | 1.52 | 5.72 | 0.0324 | 1.51 | 0.19 | 1.19 | 0.19 |
| 9 | KELT-3 | 6404 | 26 | 4.20 | 0.05 | 0.02 | 0.03 | 0.24 | 0.02 | 8.51 | 0.57 | 1.54 | 5.93 | 0.0294 | 1.77 | 0.16 | 1.28 | 0.16 |
| 10 | KEPLER-21 | 6256 | 31 | 4.02 | 0.06 | −0.07 | 0.03 | 0.11 | 0.03 | 7.38 | 0.57 | 1.50 | 5.63 | 0.0317 | 1.96 | 0.10 | 1.28 | 0.10 |
| 11 | KELT-2A | 6164 | 22 | 3.74 | 0.05 | −0.04 | 0.03 | 0.19 | 0.02 | 7.28 | 0.51 | 1.53 | 5.81 | 0.0315 | 2.01 | 0.10 | 1.27 | 0.10 |
| 12 | HD86081 | 6015 | 19 | 3.94 | 0.06 | 0.14 | 0.02 | 0.38 | 0.02 | 4.01 | 0.57 | 1.36 | 4.88 | 0.0314 | 1.63 | 0.13 | 1.18 | 0.13 |
| 13 | WASP-74 | 5727 | 14 | 3.70 | 0.03 | 0.14 | 0.02 | 0.22 | 0.02 | 8.24 | 0.38 | 1.25 | 4.58 | 0.0341 | 1.57 | 0.15 | 1.11 | 0.16 |
| 14 | HD 149026 | 6096 | 14 | 4.06 | 0.02 | 0.25 | 0.02 | 0.38 | 0.02 | 5.28 | 0.49 | 1.38 | 4.92 | 0.0302 | 1.51 | 0.10 | 1.17 | 0.10 |
| 15 | HD 209458 | 5988 | 17 | 4.17 | 0.06 | −0.22 | 0.03 | −0.01 | 0.02 | 2.96 | 0.86 | 1.26 | 4.33 | 0.0282 | 1.25 | 0.10 | 1.10 | 0.10 |
| 16 | BD-10 3166 | 5578 | 23 | 4.64 | 0.04 | 0.22 | 0.01 | 0.39 | 0.02 | 6.88 | 0.38 | 0.82 | 2.43 | 0.0361 | 0.82 | 0.17 | 0.92 | 0.17 |
| 17 | HD 189733 | 5374 | 18 | 4.89 | 0.04 | −0.04 | 0.01 | 0.09 | 0.01 | 2.75 | 0.60 | 0.59 | 1.70 | 0.0287 | 0.60 | 0.01 | 0.82 | 0.02 |
| 18 | HD 97658 | 5468 | 20 | 4.68 | 0.04 | −0.39 | 0.01 | −0.17 | 0.01 | 1.87 | 0.85 | 0.72 | 2.20 | 0.0320 | 0.62 | 0.01 | 0.84 | 0.02 |
| 19 | HAT-P-7 | 6270 | 46 | 3.95 | 0.12 | −0.01 | 0.07 | 0.43 | 0.05 | 5.70 | 1.44 | 1.53 | 5.82 | 0.0312 | 2.21 | 0.19 | 1.32 | 0.20 |
| 20 | KELT-7 | 6508 | 38 | 3.95 | 0.13 | −0.19 | 0.01 | 0.15 | 0.04 | 45.2 | 1.39 | 1.70 | 6.96 | 0.0269 | 2.01 | 0.15 | 1.34 | 0.17 |
| 21 | HAT-P-14 | 6490 | 35 | 4.12 | 0.07 | −0.11 | 0.04 | 0.09 | 0.03 | 8.86 | 0.65 | 1.63 | 6.53 | 0.0293 | 1.69 | 0.15 | 1.28 | 0.16 |
| 22 | WASP-14 | 6195 | 24 | 3.60 | 0.04 | −0.33 | 0.03 | −0.23 | 0.03 | 1.47 | 2.11 | 1.60 | 6.21 | 0.0298 | 1.50 | 0.15 | 1.19 | 0.15 |
| 23 | HAT-P-2 | 6439 | 24 | 4.05 | 0.05 | 0.15 | 0.03 | 0.29 | 0.03 | 20.66 | 0.58 | 1.62 | 6.41 | 0.0254 | 1.79 | 0.10 | 1.29 | 0.10 |
| 24 | WASP-38 | 6178 | 18 | 3.95 | 0.04 | −010 | 0.03 | 0.15 | 0.02 | 7.47 | 0.54 | 1.47 | 5.44 | 0.0301 | 1.49 | 0.13 | 1.18 | 0.13 |
| 25 | HD 118203 | 5847 | 31 | 4.06 | 0.06 | 0.04 | 0.01 | 0.19 | 0.02 | 4.16 | 0.58 | 1.20 | 4.14 | 0.0321 | 2.04 | 0.10 | 1.21 | 0.10 |
| 26 | HD 2638 | 5564 | 18 | 4.90 | 0.00 | 0.14 | 0.02 | 0.38 | 0.02 | 3.30 | 0.62 | 0.71 | 1.88 | 0.0355 | 0.72 | 0.13 | 0.89 | 0.13 |
| 27 | WASP-13 | 6025 | 29 | 3.89 | 0.03 | −0.01 | 0.03 | 0.12 | 0.03 | 2.35 | 1.30 | 1.39 | 5.01 | 0.0344 | 1.62 | 0.20 | 1.18 | 0.20 |
| 28 | WASP-34 | 5771 | 27 | 4.44 | 0.04 | −0.31 | 0.03 | 0.00 | 0.03 | 1.60 | 1.39 | 1.02 | 3.20 | 0.0326 | 1.08 | 0.20 | 1.02 | 0.20 |
| 29 | WASP-82 | 6257 | 28 | 3.96 | 0.08 | −0.05 | 0.04 | 0.22 | 0.03 | 2.86 | 1.23 | 1.52 | 5.75 | 0.0331 | 2.16 | 0.17 | 1.31 | 0.18 |
| 30 | HD17156 | 5985 | 22 | 4.10 | 0.05 | −0.06 | 0.01 | 0.09 | 0.02 | 3.02 | 0.78 | 1.29 | 4.46 | 0.0303 | 1.58 | 0.10 | 1.16 | 0.10 |
| 31 | XO-3 | 6281 | 30 | 4.16 | 0.10 | −0.12 | 0.04 | −0.19 | 0.03 | 20.2 | 0.73 | 1.47 | 5.45 | 0.0270 | 1.83 | 0.16 | 1.27 | 0.16 |
| 32 | HD 33283 | 5877 | 16 | 3.81 | 0.03 | 0.05 | 0.02 | 0.32 | 0.02 | 4.39 | 0.47 | 1.31 | 4.72 | 0.0320 | 1.99 | 0.09 | 1.21 | 0.09 |
| 33 | HD 217014 | 5755 | 12 | 4.43 | 0.03 | −0.30 | 0.01 | −0.01 | 0.02 | 0.40 | 1.43 | 1.01 | 3.18 | 0.0312 | 1.16 | 0.19 | 1.04 | 0.19 |
| 34 | HD 115383 | 5891 | 19 | 4.19 | 0.04 | −0.16 | 0.02 | 0.22 | 0.02 | 8.11 | 0.40 | 1.19 | 4.00 | 0.0285 | 1.41 | 0.01 | 1.11 | 0.02 |
| 35 | HAT-P-6 | 6442 | 34 | 4.05 | 0.05 | 0.04 | 0.02 | −0.10 | 0.03 | 11.7 | 0.71 | 1.62 | 6.43 | 0.0440 | 1.70 | 0.17 | 1.28 | 0.18 |
| 36 | HD 75732 | 5548 | 17 | 4.89 | 0.03 | 0.19 | 0.01 | 0.38 | 0.01 | 0.17 | 1.61 | 0.71 | 1.88 | 0.0338 | 0.80 | 0.19 | 0.91 | 0.19 |
| 37 | HD 120136 | 6210 | 17 | 3.79 | 0.04 | 0.20 | 0.02 | 0.20 | 0.02 | 15.14 | 0.36 | 1.55 | 5.89 | 0.0292 | 1.61 | 0.19 | 1.21 | 0.19 |
| 38 | WASP-76 | 6133 | 21 | 3.90 | 0.04 | 0.10 | 0.02 | 0.40 | 0.02 | 2.24 | 1.00 | 1.46 | 5.37 | 0.0301 | 2.03 | 0.16 | 1.27 | 0.16 |
| 39 | HN-PEG | 5853 | 18 | 4.41 | 0.04 | −0.37 | 0.02 | 0.03 | 0.02 | 10.02 | 0.41 | 1.09 | 3.46 | 0.0337 | 1.03 | 0.01 | 1.02 | 0.02 |
| 40 | WASP-8 | 5735 | 55 | 4.62 | 0.13 | 0.10 | 0.02 | 0.39 | 0.04 | 6.45 | 1.07 | 0.93 | 2.76 | 0.0308 | 0.89 | 0.19 | 0.97 | 0.20 |
| 41 | WASP-69 | 5197 | 15 | 4.90 | 0.00 | 0.22 | 0.01 | 0.30 | 0.01 | 1.18 | 1.07 | 0.46 | 1.61 | 0.0360 | 0.58 | 0.15 | 0.78 | 0.15 |
| 42 | HAT-P-34 | 6494 | 33 | 4.22 | 0.07 | 0.14 | 0.04 | 0.38 | 0.04 | 25.32 | 0.80 | 1.60 | 6.35 | 0.0287 | 1.57 | 0.19 | 1.26 | 0.19 |
| 43 | HAT-P-1 | 6142 | 24 | 4.15 | 0.06 | 0.14 | 0.02 | 0.21 | 0.03 | 5.65 | 0.66 | 1.38 | 4.91 | 0.0330 | 1.41 | 0.10 | 1.16 | 0.10 |
| 44 | WASP-94A | 5988 | 23 | 3.76 | 0.04 | 0.17 | 0.03 | 0.38 | 0.02 | 5.55 | 0.60 | 1.41 | 5.15 | 0.0338 | 1.80 | 0.17 | 1.20 | 0.18 |
| 45 | WASP-111 | 6312 | 32 | 3.94 | 0.08 | 0.05 | 0.04 | 0.30 | 0.03 | 11.57 | 0.54 | 1.57 | 6.03 | 0.0308 | 2.12 | 0.18 | 1.32 | 0.18 |
| 46 | HAT-P-8 | 6009 | 60 | 4.06 | 0.09 | 0.15 | 0.05 | −0.12 | 0.07 | 13.68 | 1.09 | 1.32 | 4.62 | 0.0365 | 1.55 | 0.16 | 0.16 | 0.16 |
Table 4 Comparison of errors
| Errors | Teff | logg | [Fe/H] | Vsini |
| (K) | (dex) | (dex) | (km/s) | |
| Standard deviations | 73 | 0.14 | 0.08 | 0.8 |
| iSpec | 25 | 0.05 | 0.02 | 0.8 |
| Valenti & Fischer | 44 | 0.06 | 0.03 | 0.5 |
| Exoplanets.org | 66 | 0.06 | 0.07 | 0.7 |
| SWEET-Cat | 52 | 0.10 | 0.04 |
Comparing with the Exoplanets.org and SWEET.cat mean uncertainties, our mean errors (standard deviations of multiple stars) are slightly larger, although still comparable to those reported in these studies. Although preliminary, this result is important as it suggests that our results based on analysis of low resolution spectra (R ≈ 20,000 ) are in good agreement with results obtained using higher resolution spectra (R higher than 50,000).
Another way to verify the consistency of our data is to compare our results with those published in Exoplanets.org (on the left in Figure 5) and in (on the right). Taken as a whole, our results seem compatible with the data reported in these two catalogs (note that the uncertainties are those of iSpec), although there are also slight notable differences. In Figure 5a, our values for Teff are slightly higher below 5800 K than the values reported by Exoplanets.org and SWEET-Cat. However, above 6000 K our temperatures are comparable with those in Exoplanets.org, while clearly lower compared to SWEET-Cat. The largest difference between our results and those of the two other surveys is for logg. Compared with Exoplanets.org (Figure 5c), our values for log are comparable within the range 4-4.7 dex, only slightly underestimated. Above 4.7 dex, our values tend to be overestimated while below 4 dex they are underestimated. These differences are amplified comparing with in Figure 5d. Once again, however, we must conclude that these differences already existed comparing Exoplanets.org with . Despite the above differences, our metallicities in Figure 5e and Figure5f are comparable with those published both by Exoplanets.org and SWEET-Cat. Once again, our results seem more similar to the former than to the latter.
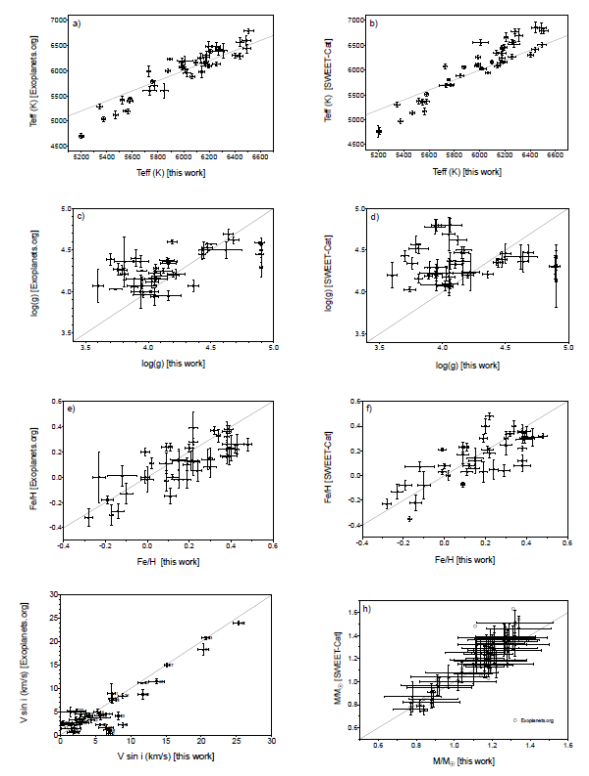
Fig. .5 Comparison of our results with those in Exoplanets.org (left) and SWEET-Cat (right): a) and b) Teff ; c) and d) log g; e) and f) [Fe=H]; g) V sin i; h) the mass of the stars, M*, with data for Exoplanets.org included.
The most important comparison for the purpose of our survey is for Vsini in Figure 5g. Unfortunately, we can only compare with Exoplanets.org, since SWEET-Cat did not publish their results. What we find is a very good agreement, with only a slight trend for our values to be higher. This trend is most probably due to our lower resolution and to the different way we determined Vmic and Vmac (more about that will be said later). In Figure 5h we compare the masses of the stars to those reported by SWEET-Cat. This time we observe a much better consistency. Note that we have also included the values given by Exoplanets.org (as open circles). In general, our masses show a weak trend to be smaller, although well within the uncertainties.
To quantify the differences between our values and those reported in Exoplanets.org and we compare in Table 5 the medians and means (note that since the numbers of stars in the comparisons vary the means and medians are not the same). In both cases, we also determined if the differences were statistically significant, using non-parametric Mann-Whitney tests (Dalgaard 2008). The last two columns in Table 5 report the of the tests and the level of significance of the differences (at a level of confidence of 95%). As one can see, the only parameter distributions that are significantly different are the surface gravity, which is slightly lower in our work than in Exoplanets.org and SWEET-Cat. The statistical test also confirms that the difference is more significant comparing our data with SWEET-Cat than with Exoplanets.org (0.0008 instead of 0.0195). Considered as a whole, therefore, these tests suggest that our results are quite comparable with those reported in the literature.
Table 5 Comparision with literature
| TIGRE (45 stars) | Exoplanets | p-value | s.l. | ||||||
| Parameter | Units | Median | Mean | Median | Mean | ||||
| Teff | (K) | 6025 | 5975 | 6095 | 5952 | 0.7679 | ns | ||
| logg | 4.06 | 4.18 | 4.26 | 4.28 | 0.0195 | * | |||
| [Fe/H] | 0.07 | 0.12 | 0.20 | 0.18 | 0.1638 | ns | |||
| Vsini | (km/s) | 5.55 | 7.39 | 4.10 | 6.92 | 0.2732 | ns | ||
| M* | (ecuacion) | 1.18 | 1.13 | 1.22 | 1.19 | 0.1010 | ns | ||
| R* | (ecuacion) | 1.57 | 1.47 | 1.34 | 1.36 | 0.0868 | ns | ||
| p-value | s.l. | ||||||||
| (l)3-4(l)6-7 Parameter | Units | Median | Mean | Median | Mean | ||||
| Teff | (K) | 6046 | 5977 | 6133 | 6036 | 0.2936 | ns | ||
| logg | 4.06 | 4.18 | 4.33 | 4.34 | 0.0008 | *** | |||
| [Fe/H] | 0.08 | 0.12 | 0.20 | 0.17 | 0.1973 | ns | |||
| M* | (ecuacion) | 1.18 | 1.13 | 1.24 | 1.18 | 0.0700 | ns | ||
As we mentioned before, as the temperature of the stars goes down, Vmic and
Vmac become comparable to Vsini and thus it is more complicated to
separate one from the others. In the Valenti &
Debra (2005) spectral synthesis analysis, the authors recognized this
problem stating, in particular, that, “...adopting a global macroturbulence
relationship should yield more accurate results than solving for Vmac in
each individual spectrum.” To determine such relation they fixed Vsini = 0,
obtaining the maximum values Vmac could have at different temperatures.
Note that these authors did not report any dependence on the spectral resolution,
although they used spectra with R between 50,000 and almost 100,000. The maximum
relation they deduced can be seen in Figure 4.
According to these authors, below Teff = 5800 K Vsini becomes negligible,
and what we measure then must be the “real” Vmac. However, this
conclusion contradicts what was expected based on the semi-empirical relation
established by Gray (1984b) and later the
minimum relation for Vmac obtained by Bruntt et al. (2010) by line modeling (the two relations can also be
seen in Figure 4). These results suggest that
applying the right macro (and micro) turbulence relationship one could obtain a
value of
In Figure 6a, we compare Vsini with the ratio Vsini/V
mac
. What we observe is that below Vsini = 4 km/s the ratio is lower than one.
As one can see in Figure 4, a value of
Vmac = 4 km/s (Vsini/Vmac = 1) corresponds to Teff ≈ 5800
K. Therefore, our results are at the same time consistent with the conclusion of
Valenti & Debra (2005), since below
Teff = 5800 K Vsini is lower than Vmac, and consistent
with Gray (1984a), Bruntt et al. (2010) and Doyle
et al. (2014), since
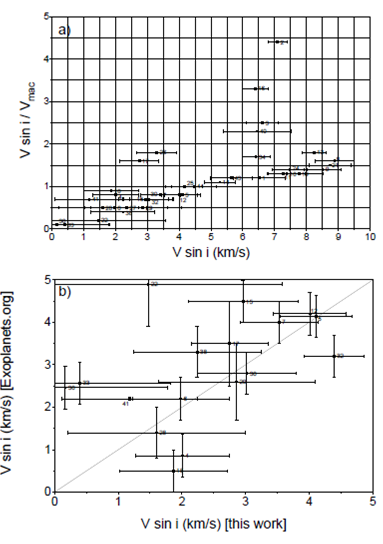
Fig. 6 a) The ratio Vsini /Vmac as a function of. Below Vsini = 4 the ratios are lower than 1. Three stars, 33, 36 and 22 have have values with uncertainties that include zero. b) Zoom of the region in Figure 5g with Vsini < 5 km/s.
Considering the results above, one expects the rotation to decrease with the temperature, but still be above zero for cool stars. Moreover, since and have found relations for Vmic and V mac that depend not only on Teff but also on on logg, we might expect a similar relation for Vsini, Teff and logg. In Figure 7, we show the diagram of Vsini and Teff for our stars. The dependence on log is shown by the gray-scale bar. In Figure 7, we also traced over our data the bi-exponential relation we obtained, together with the interval of confidence (in gray) and the prediction interval (dashed curves), which takes into account the uncertainty of each measurement. The final relation we obtained is the following:
where A = 2.20 ± 0.36, B = 0.30 ± 0.46 and C = 12.91 ± 3.59, and which has a multiple correlation coefficient of r2 = 0.6329. Except for stars 2, 3, 13 and 16, and the three stars with highest uncertainties (22, 33, and 36; not considered in this relation) all our data fit well inside the prediction interval.
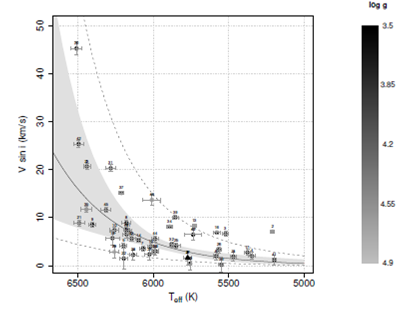
Fig. 7 Exponential relation between the rotational velocity, the temperature and the surface gravity for the 46 stars in our sample. The black triangle represents the Sun. The gray area corresponds to the interval of confidence and the dashed curves delimit the prediction interval.
Note that in order to obtain the highest correlation coefficient possible, 8 stars suspected to have peculiarly high rotation for their temperature were considered as outliers. They are, from right to left in Figure 7: 2, 3, 16, 13, 40, 39, 46 and 37. Different reasons were explored that could explain why these stars would be outliers. One is the age of the stars (e.g., Stauffer & Hartman 1986), younger stars rotating faster than older stars (see Figure 1.6 in Tassoul 2000). In Tassoul (2000) it was also shown that young stars trace the same relation of Vsini with Teff as old stars, only with higher velocities, forming an upper sequence (or upper envelope). This could be what we see in Figure 7. However, in Figure 8 the HR diagram for our stars compared to Hipparchos stars suggests that, except for three stars with slightly higher luminosity for their temperature (6, 25 and 32; none of these stars forming the envelope) all of the stars more luminous than the Sun are clearly on the main sequence. This eliminates the young age hypothesis. Another explanation could be peculiar surface activity. Since more than one phenomenon can cause such activities, the expected effect would be pure random dispersion. Checking the literature for each of the stars in our sample we did find 8 stars with reported peculiarities: 2, 3, 17, 26, 33, 37, 39 and 46. The type of peculiarities encountered included, “Flare star”, “Rotationally variable”, “Variable BY DRa”, and “Double or Multiple star”. Of these “active” stars only five in Figure 7 have a higher Vsini for their temperature: 2, 3, 37, 39 and 46. This leaves three stars (13, 16 and 40) with unexplained, relatively high Vsini values. In fact, checking their Vmac we found these stars have lower values than stars with comparable temperatures. However, in our various attempts to get the higher highest correlation coefficient possible, we judged better to keep them as outliers.
To verify our relation, in Figure 9 we traced it over the distribution of the rotational velocities and temperatures of the stars that were in our initial sample based on Exoplanets.org. As one can see, except for a few stars below Teff = 5500 K, with higher velocities, and stars below Teff = 5500 K, with lower velocities (some with Vsini = 0, the majority of the stars in this sample fall well between the prediction interval of our empirical relation. This result suggests that the decrease in angular momentum of low mass stars is a non-aleatory phenomenon, most probably reflecting the action of one specific mechanism, like, for example, magnetic braking or stellar wind (Wolff & Simon 1997; Tassoul 2000; Uzdensky et al. 2002). An exciting possibility, however, could be that this relation somehow is coupled to the formation of planets. Although this hypothesis proposed in the late 1960s was rapidly rejected, since no planet outside the Solar System was known at the time, the discovery of exoplanets allows us today to test this idea anew (e.g., Berget & Durrance 2010). This will be the subject of Paper II, in search of a connection between the formation of stars and planets.
5. Conclusions
In this study we have shown that our method of analysis developed for the TIGRE telescope using iSpec on intermediate Echelle resolution spectra yields results about the physical characteristics of stars hosting exoplanets that are comparable to those obtained using bigger telescopes and standard spectra analysis methods with high resolution spectra. Our results show that TIGRE can provide a helpful contribution in the follow-up of exoplanet surveys around bright stars, like TESS and PLATO. Such follow-up studies are essential in order to understand how the formation of planets is connected to the formation of their host stars (Eisner et al. 2020).











 nueva página del texto (beta)
nueva página del texto (beta)






