1 INTRODUCTION

Eclipsing binary systems can be divided in three groups, detached, semidetached, and contact, and are important objects for our understanding of the properties of stars, as well as stellar systems. The above sequence can be interpreted as different evolutionary stages, governed by the mass transfer of the massive component. Detached binaries (DB) that are eclipsing, exhibit Algol-type (EA type) light curves and the interactions between their components are quite weak. When one of the components of the detached binary system fills its Roche lobe, mass transfers to its companion start and a semidetached system is formed.

The continuing mass transfer produces the formation of a common envelope around the components with the consequent formation of a contact system (W UMa-type). The semidetached-contact phase is suggested by the thermal relaxation oscillation theory (TRO theory) (1976ApJ...205..208L; 1976ApJ...205..217F; 1977MNRAS.179..359R; 2005ApJ...629.1055Y; 2008MNRAS.387...97L), which predicts that binaries evolve oscillating in a cycle of contact-semidetached-contact states via mass transfer between the components. Moreover, K-type contact binaries with periods shorter than 0.3 days are important systems for explaining the period cut-off phenomenon ^{Liu et al.(2014)}. However, only few systems are well studied, especially those with periods shorter than 0.25 days. AF LMi was reported as variable star by ^{Khruslov(2007)} in his second list of new short periodic eclipsing binaries. He proposed its typology of variation as EW, as suggested by only 0.1 mag difference between the minima.

Details about the system CzeV188 were first published in the Open European Journal on Variable Stars (OEJV) nr. 185 ^{Skarka et al.(2017)} where the typology of EW variation was proposed. The present study on this system is interesting because its orbital period is below the period cut-off and because of its K spectral type.

Finally, CRTS J073333.0 + 302556 was found to be a variable star with a period of 0.267498 days and amplitude of variations of 0.16 mag, in the Catalina Surveys Periodic Variable Star Catalog ^{Drake et al.(2014)}.

2 OBSERVATIONS

Observations were done at the San Pedro Martir Observatory (Mexico) with the 0.84-m telescope (an f/15 Ritchey-Chretien), the Mexman filter-wheel and the Spectral Instruments 1 CCD detector (an e2v CCD42-40 chip with 13.5 × 13.5 μ2 pixels, gain of 1.39 e^-/ADU and readout noise of 3.54 e^-). The field of view was 7.6'×7.6' and binning 2 × 2 was employed during all the observations.

AF LMi was observed on February 3, 2016 for 0.7h, January 17, 2018 for 4.2h, April 20, 2018 for 2.3h, May 2, 2018 for 5.1h, and April, 15 2021 for 2.8h. Alternated exposures in filters B, V, R _c and I _c , with exposure times of 30, 20, 15 and 15 seconds respectively, were taken in all the observing runs.

CzeV188 was observed on July 2, 2017 for 4.7h, July 4, 2017 for 0.6h, June 12, 2018 for 4.3h, and June 13, 2018 for 0.5h. Alternated exposures in filters B, V, R _c and I _c , with exposure times of 40, 20, 15 and 15 seconds respectively, were taken in all the observing runs.

CRTS J073333.0 + 302556 was observed January 18, 2017 for 4.6h, January 28, 2017 for 7.1h, and February 3, 2017 for 6.1h. Alternated exposures in filters B, V and R _c with exposure times of 80, 30 and 15 seconds respectively, were taken in all the observing runs.

All the images were processed using IRAF¹ routines. Images were bias subtracted and flat field corrected before the instrumental magnitudes were computed with the standard aperture photometry method.

The field stars were also calibrated in the UBV(RI) _c system with the help of Landolt’s photometric standards ^{Landolt (2009)}. Based on this information we were able to choose comparison stars with colors similar to the variables (making differential extinction corrections negligible). For the case of AF LMi, star 2MASSJ10381377+3219597 (U=15.046,B=15.051,V=14.429,R=14.054,I=13.694) was employed while 2MASSJ19493362+3141488 U=14.041,B=13.008,V=11.773,R=11.121,I=10.545 was used for CzeV188 and 2MASSJ07334403+3024524 (U=19.624,B=18.355,V=16.933,R=16.079,I=15.282) in the case of CRTS J073333.0+302556. From our observations we determined the apparent magnitude m _v in quadrature for AF LMi while for Cze V188 we calculated the V magnitude using equations (23) of ^{Fukugita et al.(1996)}

All the obtained light curves are shown in Figure 6.

Any part of the data can be provided upon request.

3 PERIOD ANALYSIS AND NEW EPHEMERIS

The first ephemeris of AF LMi was proposed by ^{Khruslov(2007)} as:

Subsequently, the system was observed by the All-Sky Automated Survey for Super Novae, (ASAS-SN) (2014ApJ...788...48S; 2017PASP..129j4502K), and a more precise period of 0.4065976d was obtained. From our observations we obtained one new time of minimum (ToM) by the fourth-order polynomial fit method.

One ToM was determined for each filter and finally they were conveniently averaged to adopt one ToM per epoch. Another 56 ToMs were obtained from the 1SWASP observations ^{Butters et al. (2010)} and 8 more published in literature, were extracted from the “O-C gateway” database. The whole set of ToMs is listed in Table 1 and was used to determine new ephemeris as follows:

and the construction of the O-C diagram depicted in Figure 1.

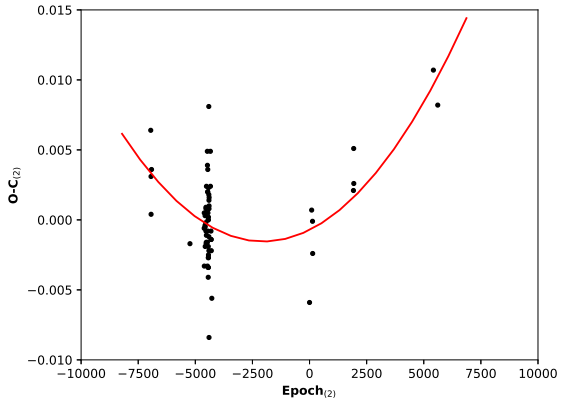
Figure 1: O-C diagram of AF LMi related to Equation 2. The solid curve shows the second order polynomial fit to the data points. The color figure can be viewed online.  

The linear square fitting to the O-C data was used to obtain the new ephemeris for all the three systems.

For CzeV188, a period of 0.250295d was firstly proposed by ^{Skarka et al.(2017)}. After new observations during the ASAS-SN survey (2014ApJ...788...48S; 2017PASP..129j4502K), a new period of 0.2474002d was suggested. The ephemeris published in the VSX database is:²

Using the ToMs obtained from our observations (Table 2) of CzeV188, determined by the polynomial fit method, we can refine its ephemeris as follow:

From our observations of CRTS J073333.0+302556 we obtained 3 ToMs (Table 3), determined by the fourth-order polynomial fit method, giving a refined ephemeris of:

4 MODELLING THE LIGHT CURVES

The latest version of the (^{Wilson-Devinney (WD) code 1971} ApJ...166..605W; 1990ApJ...356..613W; 1994PASP..106..921W; Wil16) was used and, since there are no reported spectroscopic mass-ratios of these systems, the q-search method was applied to find best initial values to be used during the light curve analysis.

The shape of the light curves of AF LMi and CzeV188 are clearly similar to those of W UMa systems, so we started our analysis directly in Mode 3 for overcontact binaries. Since CRTS J073333.0+302556 is a detached system, we used the appropriate Mode 2 in our calculations with no constrain on the potentials. CRTS J073333.0+302556 shows a flat primary eclipse covering approximately 0.040, 0.059 and 0.070 in phase respectively in the B, V and R _c filters.

To determine the mean surface temperature of the hotter star for AF LMi, we took the average value from the temperature indicated in different catalogues: LAMOST DR2 and DR5 catalogs (2016yCat.5149....0L, 2019yCat.5164....0L), ATLAS all-sky stellar reference catalog ^{Tonry et al.(2018)}, Regression of stellar effective temperatures in GaiaDR2 ^{Bai et al.(2019)} and CRTS Variable Sources Catalogue ^{Marsh et al.(2017)}. The average is 5700K.

For CzeV188 we used the color index J - K = 0.524 reported in the OEJV 185 ^{Skarka et al.(2017)} deriving the temperature from the tables of ^{Worthey & Lee(2011)}. We also used the regression of stellar effective temperatures in Gaia DR2 ^{Bai et al.(2019)}. The average temperature was found to be 5270K.

Finally, for CRTS J073333.0+302556 we used the 4027K temperature value reported by the GAIA DR2 collaboration ^{Gaia Collaboration(2018)}.

For the two contact systems, the limb-darkening parameters were interpolated with a square root law from the tables of ^{van Hamme(1993)} for log(g)=4.0 and solar abundances, while for CRTS J073333.0+302556 we used the tables of ^{Claret & Bloemen(2011)} again for log(g)=4.0 and solar abundances. A search for a solution was made for several fixed values of the mass-ratio q using as adjustable parameters the inclination of the systems i, the mean temperature of the secondaries T ₂, the surface potentials Ω1=Ω2 for the contact systems, but Ω1 and Ω2 individually for the detached one, and the monochromatic luminosities of the primaries L ₁. The behavior of the q-search for all the systems is shown in Figure 2.

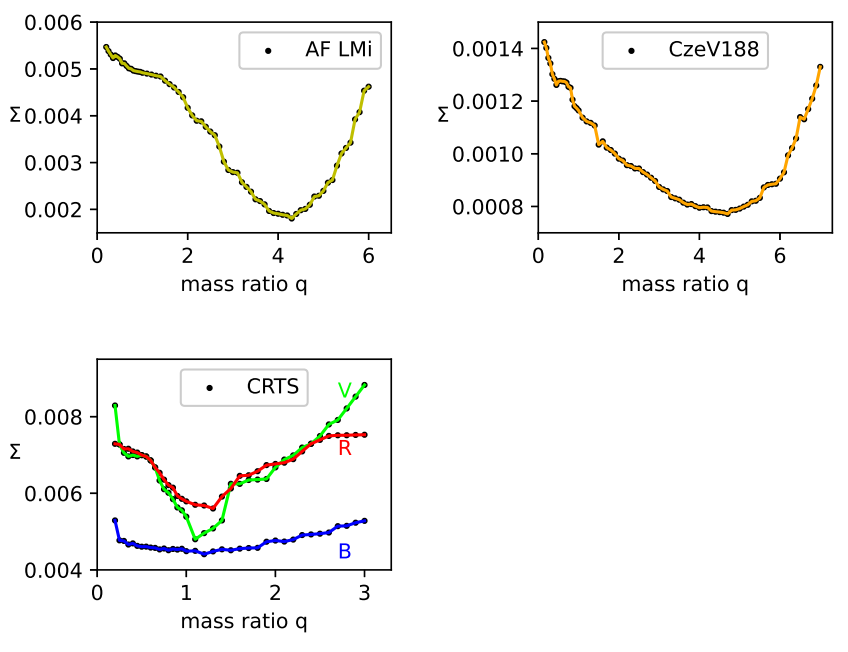
Figure 2: The relation Σ (the mean residuals for input data) versus mass-ratio q. The color figure can be viewed online. 

The value of q corresponding to the minimum of Σ (the mean residuals for input data) was included in the list of the adjustable parameters and a more detailed analysis was performed simultaneously for all the available light curves for AF LMi and CzeV188 and separately for the light curves of CRTS J073333.0+302556. The amplitude of the light curve of CRTS J073333.0+302556 decreases with the increase of the wavelength: 0.44 mags in the B filter, 0.30 in the V filter and 0.22 in the R filter, suggesting an increase in the contribution of the cooler (secondary) component to the system’s total light ^{Zakirov & Shevchenko (1982)}. The strong wavelength dependency of the primary minima of CRTS J073333.0+302556 prevent us from dealing simultaneously with the light curves. Moreover, the light curves were treated with the Iglewicz and Hoaglin’s test ^{Iglewicz & Hoaglin (1993)} in order to exclude some deviating points.

For all the three systems, it was necessary to add a spot on the surface of one component to obtain a best fit of the data.

The WD code provides the “probable” errors of the adjustable parameters, which are derived by the differential correction routine. It is known that they are unrealistically small. With the purpose of obtaining an independent estimate of the uncertainties of these parameters, we approached the problem through the Markov Chain Monte Carlo (MCMC) procedure. We generated many different data samples of the free parameters; the correlations among them from MCMC simulations and histograms of individual parameter distributions for AF LMi, CzeV188 and CRTS J073333.0+302556 are shown in Figures. 3 - 5.

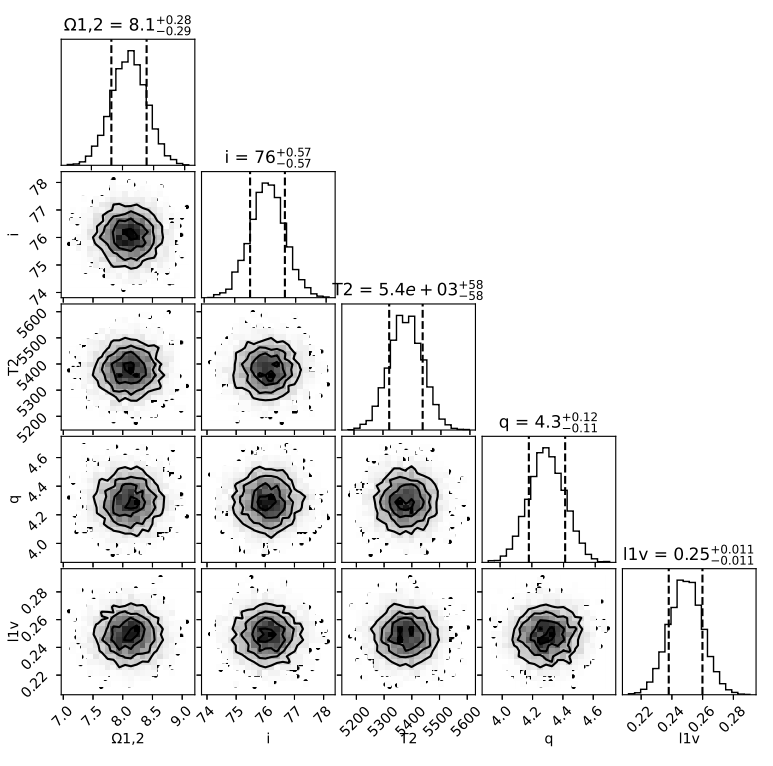
Fig. 3 Parameter correlations resulting from MCMC fit and histograms of individual parameter distributions for AF LMi.  

Fig. 4 The same of Figure 3 but for CzeV188. 

Fig. 5 The same of Figure 3 but for CRTS J073333.0+302556 in V Filter. 

The final light curve solutions, with the uncertainties derived from the MCMC procedure are reported in Tables 4 and 5, while in Figure 6 we present the filtered solution curves overlaying the data and the geometrical surface representations of the systems respectively.

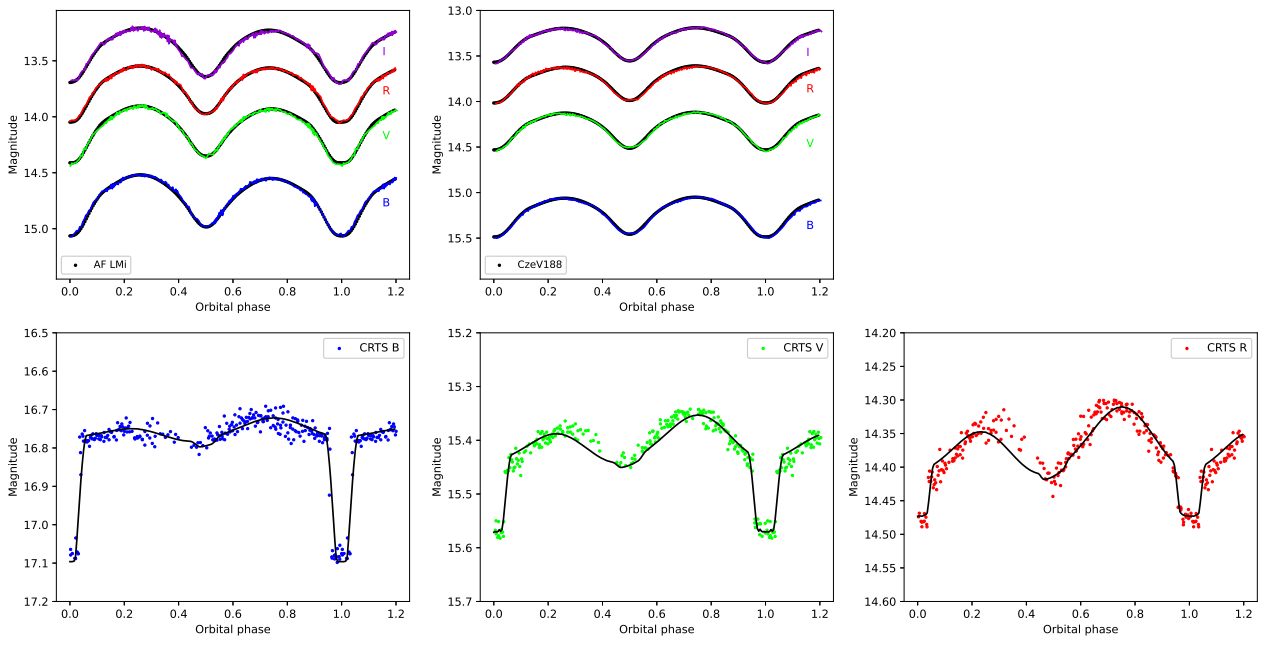
Fig. 6 CCD light curves for the three systems. Points are the original observations, color lines are the theoretical light curves. The color figure can be viewed online. 

Fig. 7 The 3D view of the stars. Left at the primary minimum, right at the quadrature. The color figure can be viewed online.  

5 ESTIMATION OF THE PHYSICAL PARAMETERS OF AF LMi AND CzeV188 WITH THE GAIA PARALLAX

Physical parameters such as mass, radius and luminosity are very important information for a contact binary system. Here we will introduce how we have estimated the physical parameters of AF LMi and CzeV188, without knowing their radial velocity curves, by using the parallaxes reported by Gaia ^{Gaia Collaboration et al.(2018)}. First, we calculated the Galactic extinction using two different methods: for AF LMi (A _v = 0.1892) the spiral model from ^{Amores & Làine(2005)} using the code GALEextin.³ For CzeV188 (A _v = 0.7285) we used the methodology of ^{Arenou et al.(1992)} since its galactic latitude is between -5° < b < +5°.

Knowing the parallax from Gaia, AF LMi p[mas] 0.986 ± 0.017 and distance d _p,c 1014.2 ± 0.017, CzeV188 p[mas] 2.260 ± 0.013 and d _pc 442.46 ± 3.60, we calculated the visual absolute magnitude M _v , the bolometric magnitude M _bol , the total luminosity L _tot and the individual luminosities L _1,2 with the following equations (e.g. ^{Chen et al. 2018}):

where m _v is the dereddened V magnitude.

Here BC is the star’s bolometric correction as interpolated from the ^{Pecaut & Mamajek(2013)} tables.

where c = L _2V /L _1V , see Table 4

The temperatures of the first and second component of the system are known, so we obtained their radii R_1,2, the semiaxis, a, and the total mass of the systems from Kepler’s third law.

where [T⊙] = 5771.8K.

where P is the period in days.

Using the value of the mass ratio from the Wilson-Devinney analysis, finally we obtained the masses M ₁ and M ₂. The values of all parameters are shown in Table 6.

6 ESTIMATION OF THE ABSOLUTE ELEMENTS OF CRTS J073333.0+302556

Due to the lack of radial velocity (RV) solutions, we used empirical relations to determine the absolute parameters of the binary systems. ^{Dimitrov & Kjurkchieva(2015)} gave a period - semi-major axis (P,a) relation on the basis of 14 binary stars having P < 0.27d which had both RV and photometric solutions, which is approximated by a parabola:

where P is in days and a is in solar radii.

Using the semi-major axis, we can calculate the radii of the binary components as R1,2=a×r1,2 mean, where r _1,2 mean is the mean fractional radii of the components. Considering a solar temperature of T⊙ = 5771.8 K, the luminosities can be calculated using the equation: L1,2=(R1,2/R⊙)2×(T1,2/T⊙)4. The mean densities of the binary components were derived from the following equation given by ^{Mochnacki(1981)}: ρ2=0.0189q/r2mean3P21+q and ρ2=0.0189q/r2mean3P2(1+q).

All the above calculated values are listed in Table 7.

The results here presented for CRTS J073333.0+302556 are a preliminary solution.

7 DISCUSSION ON THE SYSTEMS

Here we have presented the analysis of filtered CCD light curves of two contact binary systems. For both we calculated the orbital angular momentum J ₀^{Eker et al.(2006)} and their position in the logJ0-logM diagram. With a value of logJ ₀ as reported in Table 6, the systems are beyond the curved limit separating the detached and contact systems, in the region of the contact stars, which supports the shallow-contact geometric situation (Figure 8). From Figure 1, the trend of O-C (solid line) shows parabolic compositions with a rate of dP/dt=3.61×10-7±7.41-8 days year^-1. This long-term increase can probably be explained by the mass transfer from the less massive star to the more massive star. Then, if we assume conservative mass transfer, the following equation can be used to calculate the mass transfer between the components of AF LMi:

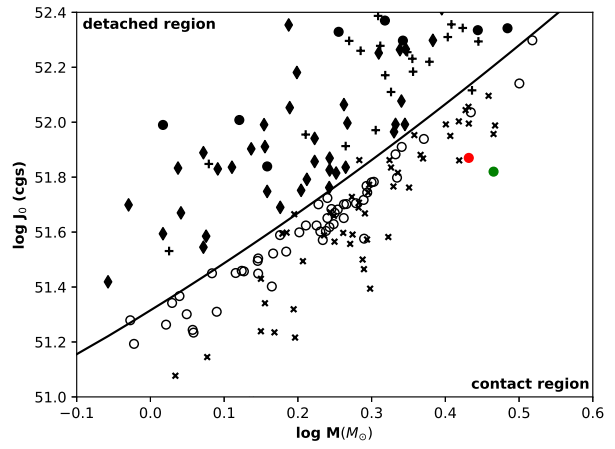
Figure 8: Position of AF LMi (red dot) and CzeV188 (green dot) in the logJ0-logM diagram. As explained in Figure 1 of the original paper of ^{Eker et al.(2006)} symbols mean: Giants (•), Sub-Giants (+), Main-Sequence (⧫), A-subtype (×), W-subtype (°). The color figure can be viewed online. 

Combining the parameters (including mass, period and rate of period variation) the rate of mass transfer was determined as

The negative sign indicates that the less massive component M ₁ is losing mass, while the more massive component M ₂ is gaining mass. As the mass ratio increases, so does the separation between the two components. The degree of contact would decrease, and AF LMi will evolve from the present contact state to the semi-contact or detached binary state.

Because the sums of the mean fractional radii of the components are rmean=0.799 and rmean=0.784, for AF LMi and CzeV188 respectively, they are in a state of marginal contact (^{Kopal, 1959}).

7.1 AF LMi and CzeV188

The values of mass ratio found for AF LMi and CzeV188 indicate that they are typical W-subtype contact binaries. A-and W-subtype are two groups of the W UMa systems divided in these subclasses by ^{Binnendijk(1965}, ¹⁹⁷⁰⁾. In the A-subtype systems the larger star is the hottest and the primary eclipse is a transit. In W-type the opposite is true: the smaller star is the hottest and the primary eclipse is an occultation. Both types of systems have a shallow fill-out value and a small difference in temperature between the components, i.e good thermal contact, these characteristics are generally accepted for overcontact systems. The ^{O’Connell effect O'Connell(1951)} that explains the different heights of the maxima, is visible; a cool spot on the secondary component of AF LMi and a cool spot on the primary component of CzeV188 (inverse O’Connell effect) were added to obtain the best fit to the light curves. The cool spot, in contrast to the hot spot, is connected with magnetic activity of the same nature as solar magnetic spots ^Mullan(1975); the hot spot is generally due to the impact of the mass transferred between the components ^{Lee et al.(2006)}. CzeV188, with its short orbital period (<0.3 days) and its spectral type K, suggests that it is near the shortest period limit. Following the work of ^{Qian et al.(2020)}, who investigated in detail the period-temperature relation using the LAMOST stellar atmospheric parameters and constructed the heat map for this relation as shown in our Figure 9 (Figure 4 in the original paper), it is possible to see that AF LMi (red dot) and CzeV188 (green dot) in this graph are located inside the boundaries for normal EW systems, but with different positions. In fact, the red and blue lines are the boundaries of the normal EW systems. Near the red line are found marginal contact systems, while those close to the blue line are deep contact ones. The objects between the two lines are normal contact EW systems.

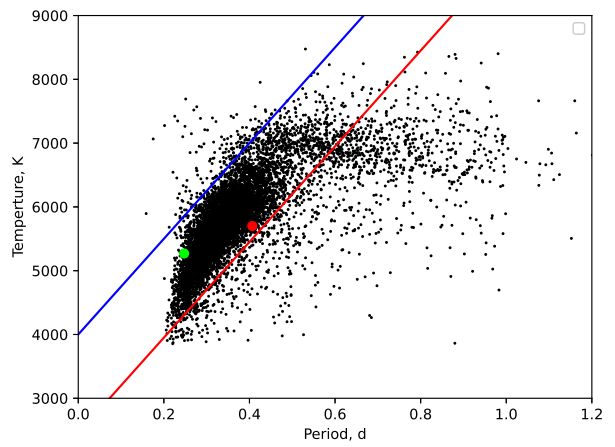
Figure 9: Correlation between orbital period and temperature based on parameters of 8510 contact binaries from ^{Qian et al.(2020)}. The position of AF LMi is marked in red, the one of CzeV188 in green. The red and blue lines are the boundaries of normal EWs. The color figure can be viewed online.  

AF LMi, with its fill-out factor and the difference in temperature between its component of some hundreds of K, is located near the red border, indicating that it could be either at the end or at the beginning of the contact phase, as predicted by the TRO theory. CzeV188 shows good thermal contact since the difference in temperature between the components is less than 100K. It is located far from the red border and near the blue one. This suggests that it is approaching the final stage of contact binary evolution.