2.1. Cluster Sample

To build our sample of galaxy clusters, we started with the compilation maintained by one of us (^{Andernach et al. 2005}, see also ^{Chow-Martínez et al. 2014}), where we included clusters for which at least N_z = 100 spectroscopic-redshifts from the literature were available. These are nearby, optically selected Abell-ACO (^{Abell et al. 1989}) galaxy clusters, with richness varying from poor to rich, and located within the redshift range 0.005 < z < 0.150. In each cluster, a galaxy is identified as a potential member when its apparent position puts it inside a projected Abell radius, RA = 2.14h70-1Mpc, and its radial velocity has a value within ± 2 500 km s−1 of a preliminary estimate for the central velocity of the system. However, its final acceptance as member will depend on a more thorough analysis, which is explained in § 3.

Our cluster sample is presented in Table 1, together with some relevant data taken from the literature. The first seven columns reproduce the original ACO data for the clusters: the cluster ID (Column 1), its equatorial coordinates, RA and Dec, in J2000 (Column 2 and Column 3), its richness (R in Column 4), distance class (D in Column 5), BM-type (BM in Column 6; ^{Bautz & Morgan 1970}) (we have converted the original scale I, II, III to 1, 3, 5 and intermediate types 2 and 4), and Rood-Sastry type when available (RS in Column 7; ^{Rood & Sastry 1971}; ^{Struble & Rood 1982}). The X-ray characteristics for each cluster are given in Columns 8 to 14: alternative X-ray name when existent (Column 8), equatorial coordinates of the X-ray emission peak (centroid position; J2000 RA and Dec in Column 9 and Column 10), the X-ray luminosity inside r₅₀₀ (Column 11; this is the radius at which the mean interior overdensity is 500 times the critical density, ρc, at the respective redshift), r₅₀₀ itself (Column 12; mostly from ^{Piffaretti et al. 2011}), and the X-ray temperature as measured by ^{Migkas et al. (2020)} in Column 13, or by others as indicated in Column 14. Note that there are new temperatures for four clusters, based on XMM-Newton and Chandra, presented for the first time in this table (see Appendix A). Finally, we list the membership of a cluster in a supercluster (Column 15), based on the Master SuperCluster Catalog (MSCC; ^{Chow-Martínez et al. 2014}), followed in Column 16 by an alternate or common name, when available, or the name of the pair when it is the case, and multiplicity, m, of the supercluster in Column 17, the multiplicity being the number of Abell clusters forming the supercluster.

This sample is well balanced in terms of BM types, covering all the possible different dynamical states: containing 17, 17, 9, 9 and 15 clusters, respectively, with BM types 1 to 5. It also follows roughly the distribution of richness of ACO clusters, clearly favoring low richness systems, in accordance with the power-law mass distribution function for clusters: 20 are classified as R = 0 (poorest; 30-49 galaxies), 24 as R = 1 (50-79), 20 as R = 2 (80-129) but only 2 as R = 3 (130-199) and 1 as R ≥ 4 (richest; {more than 200 galaxies}). However, due to the spectroscopic selection criterion, the distribution of Abell distance classes D varying from 0 to 7) is not equally represented, favoring nearby clusters. Although we cannot claim completeness, this sample can be considered a fair representation of optically selected Abell clusters at low redshifts.

Most of these clusters (59 or 88%) are detected in X-rays. Fifty-three are included in the compilation of X-ray clusters by ^{Piffaretti et al. (2011)}. The other six X-ray clusters in our sample, namely A0118, A2040, A2801, A2804, A3556 and A3716, were detected by previous surveys (respectively by ^{Kowalski et al. 1984}; ^{Stewart et al. 1984}; ^{Obayashi et al. 1998}; ^{Sato et al. 2010}; ^{Ebeling et al. 1996}, the last reference applying to the last two clusters). A3716 was also identified as a SZ source by the Planck satellite (^{Planck Collab. 2016}), with which catalog we have 43 clusters (64%) in common. The range in temperature, kT_X, is also quite large, varying from 1 to 12 keV, which is typical of low-mass to relatively massive clusters. Only 8 clusters in our sample, namely A0634, A2870, A3095, A4012, A4049, S0334, S0336 and S0906, have not yet been detected in X-rays. These might be considered as “Abell X-ray Underluminous” Cluster candidates (AXUs, for short, e.g., ^{Trejo-Alonso et al. 2014}).

2.2. Spectroscopic Data for Member Galaxies

From the information gathered in the compilation described by ^{Andernach et al. (2005)}, we retrieved, for each galaxy, the celestial coordinates and line-of-sight (LOS) heliocentric radial velocities with their uncertainties. Due to the diversity of the sources, these data are not homogeneous. To assess this problem, we treated the different quality of redshift data by adopting distinct approaches: (1) eliminating data with large (≥ 400 km s−1) estimated uncertainties, (2) eliminating obvious outliers as described further below, (3) using the average of the radial velocities for every single galaxy, (4) taking advantage of the statistics to minimize the stochastic errors (for example, calculating mean velocities and velocity dispersion for the clusters).

For the celestial coordinates, we adopted the strategy of inspecting every close pair of entries with separations larger than 3′′ (they rarely exceed 30′′), tentatively associated to the same galaxy, directly on a DSS2 image (Digitized Sky Survey, STScI) using the Aladin interface (^{Bonnarel et al. 2000}). Multiple redshift entries for the same galaxy are not uncommon and, once the multiple velocities for the same galaxy were judged consistent, we proceeded to average the different measurements, taking great care in excluding outlier values (above 3 sigma, when there are at least three independent velocity measurements). After applying this process to each cluster, we obtained a list of potential member galaxies, all with a single position, average LOS velocity and respective uncertainties (typically ± 0.5” and ± 60 km s−1, respectively, per galaxy).

2.3. Astrometric and Photometric Data of Galaxies

Although the galaxy coordinates, calculated as in the last paragraph, are precise enough, they are not homogeneous, combining more accurate positions with poorer ones. To calculate mean pairwise separations (see below), for example, we need to improve these positions. To this end, we cross-correlated the position of each galaxy in our lists with the positions in two astrometric and photometric catalogues covering the whole sky, SuperCOSMOS (^{Hambly et al. 2001a}) and Two Micron All Sky Survey (2MASS; ^{Skrutskie et al. 2006}).¹ SuperCOSMOS is a relatively deep optical survey, reaching b_J ≈ 19.5 with acceptable levels for completeness, > 95%, and contamination, < 5% (^{Hambly et al. 2001b}). Although it has good astrometry, with an uncertainty

of order ± 0.25′′ (^{Hambly et al. 2001c}), the typical uncertainty of the magnitudes is relatively large, ± 0.3 mag (^{Hambly et al. 2001b}), because it was obtained from the digitization of photographic sky survey plates. 2MASX (the catalogue of 2MASS eXtended sources), on the other hand, is a digital NIR survey reaching K_s ≈ 13.5, with nominal levels of completeness and contamination respectively of > 90% and < 2%. Although the uncertainty in astrometry is about the same as in SuperCOSMOS (0.3′′, for extended sources), the quality of the magnitudes is better, with a typical uncertainty ± 0.03 (^{Jarrett et al. 2000}). Also, since the NIR is less affected by dust extinction (e.g., ^{Fitzpatrick 1999}), the K-correction is minimal (e.g., ^{Fukugita et al. 1995}; ^{Chilingarian et al. 2010}) compared to the optical. Particular care is devoted to the photometry of the brightest galaxies in 2MASS because the data come mostly from a special catalogue, the Large Galaxy Atlas (^{Jarrett et al. 2003}), which is dedicated to galaxies that are more extended than 1′.

The only drawback of 2MASS is the depth of the survey: at the magnitude limit K_s ≈ 13.5 the mean redshift of galaxies is z ≈ 0.08 (^{Jarrett 2004}). This implies that only a fraction (about 50%) of the galaxies, the brightest in our sample, have an entry in 2MASX. Another disadvantage is the limited capacity of 2MASS to separate galaxies that are very close in projection, which is the case of faint “dumbbell” CDGs/SDGs in our sample (although this does not happen for galaxies in the Large Galaxy Atlas). SuperCOSMOS performs better in “deblending” galaxies, but then fails in accuracy determining their magnitudes once they are separated, their brightness being usually underestimated. Therefore, although we matched our data with the astrometric and photometric data in both catalogues, for the sake of homogeneity we used only 2MASS in the present paper. Absolute magnitudes for the BCGs were calculated after correcting for Galactic extinction, using the recalibration done by ^{Schlafly & Finkbeiner (2011)} of the dust maps of ^{Schlegel et al. (1998)}, and applying a K-correction as determined by ^{Chilingarian et al. (2010)}.

3.1. Central and Substructure Dominant Galaxies and the Definition of the Cluster Center

In any cluster, group or substructure of galaxies we classify as SDG/CDG the galaxy that, being among the BCGs, occupies the most central position around the gravitational potential well of its (sub-)system. From a practical observational point of view, a CDG/SDG must be coincident or very close to the local surface density peak in the sky distribution of the member galaxies. This also implies that its position is expected to be located near the X-ray emission peak (c.f. § 4.4) when this emission is detected.

In each substructured cluster, we identify (based on criteria to be explained below) one substructure as the “main” (or gravitationally dominant) substructure and adopt its SDG as the CDG for the whole system. Also, as a general rule, we adopt the position of the CDG/SDG as the location of the dynamical center of the cluster/substructure.

In the literature, the physical characteristics of the BCG are commonly used as a trade mark of its system. However, identifying which galaxy is the BCG obviously depends on which band-pass is used. For example, a very bright spiral galaxy, especially in a starburst phase, in the outskirts of a cluster, could easily be brighter in B or V than a giant and red elliptical near its center (e.g., NGC1365 in Fornax/S0373). This is why we define our BCGs to be more luminous in K _s, which is a better proxy for the stellar mass of galaxies, and thus consistent with the idea that a CDG/SDG should also be the most massive galaxy of its cluster/substructure.

Adopting these definitions, in 81% of our cluster sample we found the CDG to be coincident with the original BCG, according to prescriptions given by, for example, Abell (or others like ^{Bautz & Morgan 1970}; ^{Rood & Sastry 1971}; ^{Struble & Rood 1982}). However, in the remaining 19% of the clusters the BCG is not the CDG, for one of the following three reasons: (i) the BCG is really a SDG, like in the case of Fornax (NGC 1316), forming 13% of our cluster sample (we classified them as “Fornaxlike” clusters); (ii) the BCG is located close to the center of the cluster (as confirmed by X-ray emission or based on other dynamical analyses) but is only slightly brighter than the real CDG, as in Coma (BCG: NGC4889, CDG: NGC4874), forming 4% of our sample (they are classified as “Coma-like” clusters); (iii) the BCG is a giant elliptical galaxy located at the periphery of the cluster, forming 2% of our sample (we classify these galaxies as “fossil group candidates”, without, at this point, gathering more data to confirm this candidacy).

3.2. Cluster Membership

When clusters are separated by less than 6 h70-1 Mpc on the sky, the areas subtended by their R_A overlap. There are 38 clusters in our sample for which this is the case. To separate the members (or populations) of these clusters, we first merged the lists of their potential member galaxies, eliminating the duplicated entries as assigned by different sources in the literature to the different systems. Then we proceeded to separate the galaxies that are members of each cluster, by applying a method similar to the one described in § 3.4 for identifying substructures.

To double-check our results, we also applied to the superposed clusters a two-body Newtonian criterion for gravitationally bound systems (see ^{Beers et al. 1982}, and § 3.5). The results (bound vs. unbound) obtained by this process are in good agreement with previous results in the literature (^{Gregory & Thompson 1984}; ^{Krempéc-Krygier et al. 2002}; Pearson & Batuski 2013; ^{Yuan et al. 2005}). It is worth noting that 4 of the 11 bound complexes in Table 2 are consistent with supercluster “cores” (Zúñiga et al., in preparation); those are: Her-C (MSCC 474), Scl (MSCC 033), HorRet-B (MSCC 115) and Shapley (MSCC 389). Among the other bound systems, three are typical pairs, A0399-A0401, A2052-A2063A and A3530-A3532, and four, A0122-A0118, A2199-A2197, A2877-A2870 and A4038A-A4049, are examples of a massive cluster (main cluster, first of the pair) linked by a filament made of various groups (secondary system; c.f. § 4.2).

After homogenizing the galaxy coordinates by applying the match with photometric data, and after defining the different centers and correcting for superposed clusters, we proceeded to check the membership of the galaxies in their respective clusters using a more robust approach. The principle is simple: considering that, in a gravitationally-bound system, the galaxies must have velocities that do not exceed the escape velocity, their distribution in a projected phase-space (PPS) diagram, formed by the LOS velocity as a function of projected cluster-centric distance, e.g., Figure 1, must be enclosed within a trumpet-shaped curve, usually called “caustic”, as defined by the escape velocity (e.g., ^{Regös & Geller 1989}; ^{López-Gutiérrez et al. 2022}). Details about the method for defining and fitting caustics are presented in ^{Chow-Martínez (2019)}. In Figure 1, all the galaxies falling outside the caustic for the cluster A0085 are discarded, leaving only those that are considered as gravitationally bound.

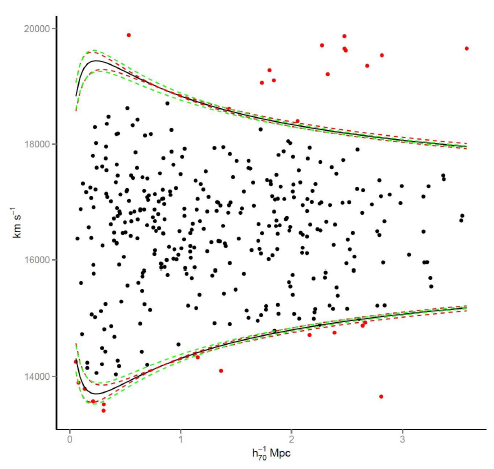
Fig. 1 Example of applying the caustics method to the cluster A0085; the caustics are the black solid lines, while the red dashed lines indicate the rms of the fit and the green dashed lines the bootstrap uncertainty (1 000 simulations). Black points (that is, the ones within the caustics) are taken to be the bound members, while red points are discarded as cluster members. The color figure can be viewed online. 

Applying the caustics analysis, we found that on average 10% of the candidate member galaxies in each cluster, at least in relatively isolated systems, must be discarded. For the overlapping clusters above, these galaxies are usually bound to another cluster of the complex. Obviously, no single galaxy is assigned to more than one cluster.

3.3. Determination of Cluster Dynamical Parameters

To establish the dynamical properties of each system, we first measure two robust kinematical parameters, known as the biweight central value, C _BI, and scale, S _BI (^{Beers et al. 1990}). Using these parameters, we calculate preliminary values for the systemic radial velocities, v _c, and velocity dispersions, σ_c, considering the N _c members. Then we proceed by defining, for each cluster, a projected aperture on the sky consistent with the virial radius.

This implies first estimating r ₂₀₀, the radius inside which the mean density of galaxies exceeds 200 × ρ_c at the redshift of the cluster. Following the prescription by ^{Carlberg et al. (1997)}:

Where

H(z)=H0Ωr(1+z)4+Ωm(1+z)3+Ωk(1+z)2+ΩΛ, assuming Ω_r (radiation) and Ω_k (curvature) are about zero. Since the virial radius depends on the redshift and cosmology (e.g., ^{Bryan & Norman 1998}), a local value of 1.3 × r ₂₀₀, corresponding to about r100, is usually adopted (e.g., ^{Kopylova & Kopylov 2018}). Once the circular aperture corresponding to the virial radius is determined, we counted the number of galaxies inside it, N _α, and recalculated the systemic radial velocity, v _cl, and its velocity dispersion, σ_cl, using once again CBI and S _BI.

These N _α galaxies are also used to calculate the projected radius, R _p, equal to twice the harmonic mean projected separation, using the relation:

where r _ij is the pairwise projected separation between galaxies. Estimation of the virial mass, M _vir, follows the relation:

where the factor α quantifies the isotropy level of the system (α = 3 when complete isotropy is assumed), applied to σ_cl, while the factor π/2 is applied to deproject R _p (^{Limber & Mathews 1960}). Finally, the virial radius is obtained using the relation:

where the virial density is defined as ρ_vir = 18π²(3H ²(z)/8πG).

3.4. Substructure Analysis

Several tests, in different spatial dimensions, have been proposed for the detection of substructures in galaxy clusters based on optical data: in 1D, as applied to the redshifts (e.g., ^{Bird & Beers et al. 1993}; ^{Hou et al. 2009}), in 2D, as applied to galaxy projected celestial coordinates (e.g., ^{Geller & Beers 1982}; ^{Fitchett & Webster 1987}; ^{West et al. 1988}; ^{Kriessler & Beers 1997}; ^{Flin & Krywult 2006}), and in 3D, as applied to both redshifts and coordinates (e.g., ^{Dressler & Shectman 1988}; ^{Serna & Gerbal 1996}; ^{Pisani 1996}; ^{Einasto et al. 2010}; ^{Yu et al. 2015}). However, not all these tests have the same efficiency. Through a study of 31 different tests, ^{Pinkney et al. (1996)} found the 3D-test developed by ^{Dressler & Shectman (1988, DS herafter)} to be the most sensitive, concluding that, in general, the higher the dimension of a test, the more powerful it is in distinguishing substructures. This was confirmed subsequently by ^{Einasto et al. (2012)}, who also showed that 3D-tests are more robust than 2Dtests, and 2D-tests more robust than 1D-tests. However, both groups recommended the application of more than one test.

Tests for detecting substructures using X-ray data have also been proposed (e.g., ^{Mohr et al. 1993}; ^{Buote & Tsai 1995}; ^{Andrade-Santos et al. 2012}). However, because the tests are based on X-ray surface brightness, the detection of substructures is usually limited to the densest, most concentrated (R < r ₅₀₀) regions of the clusters (e.g., ^{Piffaretti & Valdarnini 2008}), which might complicate comparisons with substructures detected in the optical. In the study made by ^{Lopes et al. (2018)}, for example, only ≈ 60% of the substructures detected in optical were also detected in X-ray, both inside r ₅₀₀. They also found the fraction of substructures to increase with the aperture used, as well as with the mass of the cluster and its redshift (up to z ≈ 1; see also ^{Jeltema et al. 2005}). Although these trends are consistent with various levels of relaxation (for example, clusters being less relaxed in the past than now), establishing a firm connection, as well as a time scale to reconstruct the assembly histories of clusters, is not straightforward and needs independent confirmation.

In principle, this is what a study of the CDG dynamical characteristics can contribute. More specifically, the projected position offset of a CDG relative to the X-ray peak and its peculiar velocity relative to the centroid of the distribution of galaxy members are two parameters expected to be correlated with the level of relaxation of the clusters (e.g., ^{Zhang et al. 2011}; ^{Lavoie et al. 2016}; ^{Lopes et al. 2018}): the smaller the offset and peculiar velocity, the higher the level of relaxation. This assumes that migration through dynamical friction of the CDG towards the center of the cluster is less rapid than that of the hot gas. Comparing these two parameters with the level of substructuring in clusters -the higher the number of substructures the lower the level of relaxation- should consequently complement our view about their assembly histories.

Thus, to reconstruct the assembly histories of the clusters in our sample, we will develop our study of substructures applying different tests, with different dimensions, in the optical, comparing with X-ray substructuring information and radio data from the literature whenever available, and each time comparing the results (as an independent test) with the dynamical characteristics of the CDGs in their respective clusters.

Radial velocity distributions (1D test): We start by directly inspecting the LOS velocity distributions of galaxies within the clusters, comparing them with a Gaussian distribution. The physical motivation of this test is the following: as the system tends toward relaxation, the absolute values of skewness and excess kurtosis (with respect to the value of 3 for a Gaussian distribution) also tend to decrease. This is a straightforward test that is easy to quantify.

Adopting a level below 0.3 as an upper limit for relaxation, only 25% of the clusters in our sample present LOS velocity histograms consistent with a Gaussian. This indicates that as much as 75% of the clusters in our sample show a possible signal of being substructured, as disclosed, more specifically, by two or more noticeable peaks in the LOS velocity distribution or platykurtic kurtosis values.

Projected distribution of galaxies (2D-test): The second test consists in tracing the isodensity contour map of the projected galaxy distribution in each cluster, where any galaxy density peak may be considered as a significant substructure (Geller & ^{Beers 1982}) since only spectroscopically confirmed members were considered. The (probability) density maps were obtained using a bivariate adaptive kernel, fitted by the function:

where z (do not confuse with redshift) is equal to:

and where, when the parameters x, y are not strongly correlated, one can assume ρ = 0.

In Figure 2 the surface density map of the member galaxy distribution of the cluster A0085 is shown as example. In this figure, the isodensity contours are codified in colors, with a cross indicating the density peak. Also shown are the positions of the CDG (open square) and peak in X-ray (× symbol). Note that although the CDG is slightly off-centered from the distribution of the galaxies, its position is almost the same as the peak in X-ray. Despite the substructures, this looks like a relatively well evolved cluster.

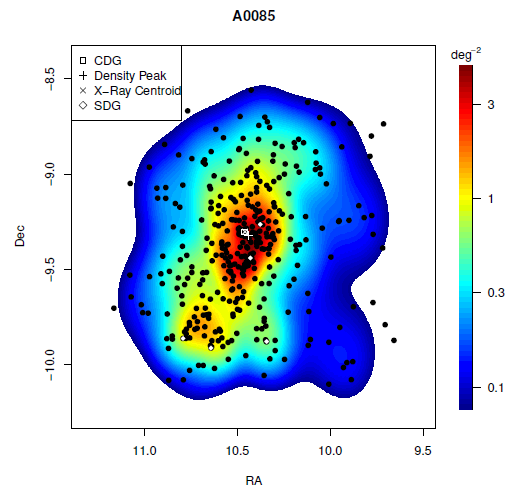
Fig. 2 Example of an isodensity map for the cluster A0085. The isodensity levels are coded by colors, in units of the probability density to find spectroscopic member galaxies/deg2 (mean probability density equals to 1). The position of the peak in density is indicated, as well as the position of the CDG, SDGs and X-ray centroid. The color figure can be viewed online. 

As it is difficult to resume the information on substructure in a table we offer the isodentity maps of all of our clusters on an accompanying web site (www.astro.ugto.mx/recursos/HP_SCls/Top70.html).

X-ray surface brightness maps (2D- test): X-ray surface brightness maps are constructed and used as supplementary information for identifying the substructures. Apart from applying an algorithm to independently detect substructures in these data, we checked every substructure detected in the optical for its counterpart in X-rays. This made possible, for example, to find cases of multimodal main structures that would not be identifiable from the optical data alone.

Using the Aladin interface, we traced the X-ray surface brightness maps for all our clusters, overlaid in red contours on top of the respective DSS2 Rband² image. The X-ray data come from ROSAT³ soft band (surface brightness in the 0.1-2.4 keV). It is worth to note that the all-sky sensitivity of ROSAT is limited to about 10−13 erg s−1 cm−2 (e.g., ^{Vikhlinin et al. 1998}; ^{Burenin et al. 2007}). This is enough for detecting kT_X ≥ 1 keV clusters, but not enough for identifying substructures in the cooler ones. All these maps can also be examined in the webpage accompanying this article.

The example shown in Figure 3 is once again for A0085. A smoothing parameter of 4 in ds9 was used. The lowest contour in X-ray was traced at the 3σ level, followed by contours at levels of 6, 12, 24 and 48 σ. The cyan × symbol is the X-ray peak emission, the magenta square locates the CDG and the green circle corresponds to a 0.5 h70-1 Mpc radius around it. Usually, an optical image of size 30′×30′ in the plane of the sky is sufficient to show the distribution of the X-ray emission. Comparing with Figure 2, one can see that the detected gas in A0085 covers a smaller area (volume) than the distribution of the galaxies in the cluster, and that the CDG is only slightly displaced from the X-ray peak.

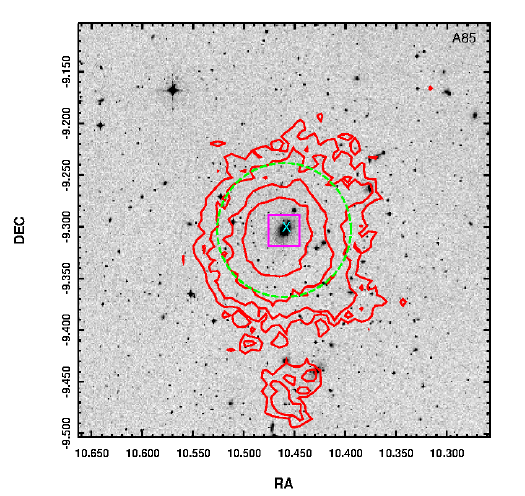
Fig. 3 Example of an X-ray map (red contours over the DSS image), for the cluster A0085. The position of the X-ray peak is indicated (cyan ‘×’ symbol), as well as the position of the CDG (magenta square). The green circle marks a 0.5 h70-1 Mpc radius around the CDG. The color figure can be viewed online. 

Dressler & Shectman test (3D-test): The DStest (^{Dressler & Shectman 1988}) is performed in two steps. The first step consists in calculating the δ_i parameter for each member galaxy:

where v _c and σc are the cluster global parameters, while v¯local and σ_local are local parameters, calculated for the N _nn = 10 nearest neighbors of each member galaxy (see ^{Bravo-Alfaro et al. 2009}, for a discussion of these local parameters and the number of nearest neighbors).

The second step consists in calculating, for each cluster, the parameter Δ = Σδ_i and comparing its value with a set of 1000 Monte Carlo simulations, obtaining the probability p that a value Δ > Δ_observed would have been obtained by chance. We, thus, calculate P _sub = 100 ∗ (1 − p), which is the probability that the cluster is substructured. Based on this test, a cluster with P _sub > 90% can be considered to be significantly substructured.

Because Δ tends to equal the number of galaxy members when the cluster is close to relaxation (e.g., ^{Pinkney et al. 1996}), we used the ratio Δ/N _c as an iterative parameter for the test. Note that, differing from the traditional way substructures are identified by this test, we do not consider only specific concentrations of galaxies with high δ values in the projected distribution.⁴ Specifically, when Δ/N _c > 1.2, we analyse both the 3D distribution of galaxies in RA, Dec and v _local and the respective 2D PPS diagram to identify, in the former, the volume separation surfaces between the substructures (e.g., ^{López-Gutiérrez et al. 2022}). In this pseudo-3D volume, substructure members are more smoothly distributed, defining a more isolated locus (local concentration) than in a RA-Dec-z-volume, while in the PPS they show the typical caustics-shape distribution. Therefore, after separating the substructures from the remaining main structure, we recalculate Δ/N _c to see whether it is below 1.2, and if not, iterate again to isolate new substructures.

Note that in applying this test there are cases for which it is not correct to assume there is only one main structure. This happens when there are two or more substructures that are comparable in mass, as well as being much more massive than all the other substructures in the cluster. These are examples of “bimodal” or “multi-modal” clusters.

The parameters calculated from the dynamical and substructure analyses are reported in Table 3. In Column 1, we give the updated cluster ID. Note that the entries in Table 3 slightly differ from those in Table 1. More specifically, the clusters A2870 and A4049 were determined (see § 3.2) to be part of other massive clusters, respectively A2877 and A4038A. On the other hand, two clusters had their well-known LOS components considered separately, A1736 becoming A1736A and A1736B, and A3526 becoming A3526A and A3526B. Consequently, although the number of entries in both tables are the same, 67 clusters, their identities are somewhat different. In Table 3, the equatorial coordinates of the corresponding CDGs (and by convention, cluster centers) are given in Columns 2 and 3, followed in Column 4 by their LOS velocities. Column 5 reports the number of candidate members after splitting up the intersecting neighbors, Ng, and Column 6, the number of galaxies, N _c, considered to be bound (included within the caustics) in each cluster. Other dynamical parameters are reported in Column 7 (v _c), Column 8 (σ_c), both for the N _c members, Column 9 (r ₂₀₀), Column 10 (N _α), Column 11 (v _cl), Column 12 (σ_cl), the last three for the members inside the circular aperture, Column 13 (R _p), Column 14 (R _vir) and Column 15 (M _vir). Parameters associated to the substructure analyses are shown in Columns 16 to 18: the skewness, the excess kurtosis, and P _sub = 100 ∗ (1 − p), respectively.

TABLE 3: BASIC DATA ON CLUSTERS OF THE SAMPLE 

IDa (1)	RACDG [deg]J2000 (2)	DecCDG [deg]J2000 (3)	vCDG [km/s] (4)	Ng (5)	Nc (6)	vc [km/s] (7)	σc [km/s] (8)	r200 [Mpc]b (9)	Nα (10)	vcl [km/s] (11)	σcl [km/s] (12)	Rp [Mpc]b (13)	Rvir [Mpc]b (14)	Mvir [M⊙] (15)	skew (16)	kurt (17)	Psub [%] (18)	Nsub m,hs,ls (19)	A (20)	rox [kpc]b (21)	vpec [km/s] (22)
A2798B	9.37734	-28.52947	33338	81	78	33604	697	1.353	60	33544	757	1.148	1.748	6.01	-0.313	-0.502	87.4	1,0,0	U	96.5	-185.3
A2801	9.62876	-29.08160	33660	50	45	33773	652	1.259	35	33640	699	1.553	1.833	6.94	-0.397	-0.024	15.5	1,0,0	U	42.4	18.0
A2804	9.90753	-28.90620	33546	88	80	33378	663	1.292	48	33669	516	1.277	1.403	3.11	-0.346	-0.982	97.6	2,0,0	M	126.3	-110.6
A0085A	10.46051	-9.30304	16613	368	352	16561	1011	2.027	321	16570	1045	2.030	2.668	20.20	-0.444	-0.118	99.9	1,2,3	S	8.2	32.2
A2811B	10.53717	-28.53577	32466	146	139	32354	831	1.625	103	32329	947	1.701	2.316	13.90	0.162	-0.042	94.3	1,0,2	S	5.5	123.7
A0118	13.74348	-26.37515	34068	119	80	34384	681	1.341	59	34287	689	1.206	1.667	5.23	0.349	-0.635	90.4	1,2,0	S	・ ・ ・	-212.7
A0119	14.06709	-1.25549	13323	339	333	13299	810	1.633	294	13301	853	1.430	2.082	9.51	-0.175	0.246	99.9	1,2,1	S	125.2	21.1
A0122	14.34534	-26.28134	33804	111	31	34076	659	1.265	28	34062	677	1.190	1.641	4.98	0.337	-0.266	46.8	1,0,0	U	50.6	-231.7
A0133A	15.67405	-21.88215	17048	137	132	16830	713	1.425	86	16838	778	1.320	1.899	7.30	0.077	-0.393	77.7	1,2,0	S	33.9	198.8
A2877-70	17.48166	-45.93122	7213	237	174	7034	652	1.326	112	7143	679	0.999	1.596	4.20	0.273	-0.398	100.0	1,2,0	S	27.8	68.4
A3027A	37.70600	-33.10375	23541	167	102	23429	668	1.335	82	23494	713	1.618	1.904	7.52	-0.278	-0.814	97.2	1,1,1	S	113.9	43.6
A0400	44.42316	6.02700	6789	115	61	6959	323	0.682	51	6947	343	0.635	0.870	0.68	0.100	-1.007	76.0	1,1,0	S	39.8	-154.4
A0399	44.47119	13.03080	21483	101	69	21138	957	1.894	69	21146	950	1.414	2.209	11.70	-0.225	-0.460	13.3	1,0,0	U	110.1	314.8
A0401	44.74091	13.58287	22297	116	115	22053	1028	2.036	114	22061	1026	1.574	2.407	15.10	0.263	-0.352	40.8	1,0,0	U	18.6	219.8
A3094A	47.85423	-26.93122	20552	126	114	20489	548	1.090	84	20539	637	1.305	1.648	4.83	0.628	0.243	88.3	1,0,0	U	148.3	12.2
A3095	48.11077	-27.14016	19314	44	40	19485	306	0.606	21	19557	327	0.664	0.845	0.65	-0.018	-0.932	10.5	1,0,0	L	・ ・ ・	-228.1
A3104	48.59055	-45.42024	21785	62	53	21777	413	0.823	28	21681	498	0.782	1.178	1.77	0.039	-0.106	39.5	1,2,0	S	34.4	97.0
S0334	49.08556	-45.12110	22401	22	27	22373	518	1.030	26	22363	534	0.811	1.249	2.11	0.449	1.037	27.4	1,0,0	L	・ ・ ・	35.4
A3112B	49.49025	-44.23821	22764	120	97	22631	672	1.337	74	22669	705	1.861	1.982	8.46	0.271	-0.572	99.9	1,1,0	S	13.2	88.3
S0336	49.45997	-44.80069	22849	54	44	23223	506	1.006	32	23186	538	1.140	1.405	3.02	0.178	-0.606	3.2	1,0,0	L	・ ・ ・	-312.8
A0426A	49.95042	41.51167	5231	360	314	5254	1030	2.104	314	5262	1029	1.395	2.359	13.50	0.030	-0.535	97.1	1,0,2	P	4.0	-30.5
S0373	54.62118	-35.45074	1452	272	229	1452	334	0.688	98	1461	390	0.308	0.749	0.430	-0.025	-0.428	100.0	1,2,1	S	1.7	-9.0
A3158	55.72063	-53.63130	17327	258	249	17764	1064	2.138	249	17735	1066	1.341	2.353	13.90	0.260	-0.478	49.6	1,2,2	S	19.1	-385.2
A0496	68.40767	-13.26196	9841	358	351	9892	688	1.395	279	9925	712	1.364	1.822	6.31	0.030	-0.535	99.9	1,1,0	S	8.5	-81.3
A0539	79.15555	6.44092	8257	143	132	8679	571	1.160	92	8631	698	0.882	1.557	3.92	-0.249	0.825	100.0	1,2,0	S	6.5	-363.5
A3391	96.58521	-53.69330	16361	119	100	16831	760	1.519	75	16776	817	1.270	1.936	7.74	0.159	-0.482	9.8	1,0,0	U	24.4	-393.0
A3395	96.90105	-54.44936	14571	224	218	14875	722	1.450	199	14878	746	1.264	1.823	6.42	-0.158	-0.494	100.0	2,2,1	M	10.9	-292.5
A0576	110.37600	55.76158	11435	238	220	11351	810	1.638	191	11350	866	1.633	2.202	11.20	0.031	-0.114	100.0	1,2,0	S	84.3	81.9
A0634	123.93686	58.32109	8029	140	132	8006	318	0.646	70	8037	395	0.792	1.029	1.13	0.057	-0.061	73.4	1,0,0	L	・ ・ ・	-7.8
A0754	137.13495	-9.62974	16451	468	386	16246	757	1.520	333	16258	820	1.484	2.045	9.10	-0.024	0.373	100.0	2,2,2	M	239.1	183.1
A1060	159.17796	-27.52858	3808	382	380	3709	652	1.335	343	3694	678	0.951	1.574	3.99	0.122	-0.532	100.0	1,0,5	P	4.9	112.6
A1367	176.00905	19.94982	6260	339	286	6451	547	1.115	226	6444	597	1.157	1.539	3.76	-0.026	-0.629	100.0	2,0,2	M	366.0	-180.1
A3526A	192.20392	-41.31166	2948	235	235	3088	491	1.005	126	2993	564	0.836	1.335	2.43	-0.482	-0.191	100.0	1,0,3	P	3.8	-44.6
A3526B	192.51645	-41.38207	4593	101	95	4580	276	0.552	45	4636	317	0.480	0.754	0.44	0.300	-0.359	99.9	1,1,0	S	・ ・ ・	-42.3
A3530	193.90001	-30.34749	16187	126	110	16036	615	1.231	94	16064	631	1.272	1.632	4.63	0.305	-0.567	99.5	1,1,0	S	66.5	116.7
A1644	194.29825	-17.40957	14225	307	301	14085	987	1.989	288	14095	1008	1.507	2.365	14.00	-0.049	0.201	86.6	1,0,2	P	39.6	124.2
A3532	194.34134	-30.36348	16303	112	103	16753	423	0.849	58	16709	443	0.929	1.160	1.66	-0.130	-0.798	93.5	1,2,0	S	87.9	-384.6
A1650	194.67290	-1.76139	25328	220	192	25216	673	1.330	146	25249	723	1.581	1.903	7.55	0.188	0.016	2.1	1,0,0	U	27.3	72.9
A1651	194.84383	-4.19612	25622	221	191	25454	833	1.651	158	25453	876	1.782	2.250	12.50	0.132	-0.569	59.2	1,0,2	P	25.5	155.8
A1656	194.89879	27.95939	7157	969	969	6976	993	2.025	919	6997	995	1.734	2.474	15.70	-0.100	-0.018	100.0	1,1,8	S	57.9	156.4
A3556	201.02789	-31.66996	14406	102	102	14435	505	1.016	90	14436	520	1.048	1.347	2.59	0.354	-0.606	99.0	2,0,0	M	630.5	-28.6
A1736A	201.68378	-27.43940	10506	74	74	10363	417	0.840	36	10499	386	0.955	1.075	1.30	0.102	-0.997	100.0	1,3,0	S	・ ・ ・	6.8
A1736B	201.86685	-27.32468	13574	145	141	13665	839	1.689	126	13678	844	1.355	2.029	8.82	0.022	-0.500	99.0	1,1,1	S	610.8	-99.5
A3558	201.98701	-31.49547	14073	548	548	14455	950	1.912	469	14476	955	1.893	2.460	15.80	-0.230	-0.478	100.0	1,0,1	P	25.0	-384.4
A3562	203.39474	-31.67227	14693	231	98	14541	564	1.138	82	14561	594	1.221	1.549	3.94	0.037	-0.634	43.6	1,0,0	U	42.6	125.9
A1795	207.21880	26.59301	18968	179	164	18893	764	1.525	154	18889	780	1.278	1.876	7.09	-0.049	0.210	98.3	1,0,0	U	13.8	74.3
A2029	227.73376	5.74491	23353	202	155	23052	934	1.850	155	23051	931	0.989	1.931	7.82	0.096	-0.791	92.8	1,0,0	U	132.8	280.4
A2040B	228.19781	7.43426	13713	153	150	13472	567	1.141	104	13527	627	1.327	1.653	4.77	0.312	0.026	97.8	1,1,0	S	43.3	178.0
A2052	229.18536	7.02167	10332	178	176	10295	581	1.179	120	10416	648	1.115	1.600	4.28	0.356	0.003	100.0	1,1,0	S	9.1	-81.2
A2065	230.62053	27.71228	21828	204	169	21889	1043	2.071	168	21878	1043	1.712	2.504	17.00	0.129	-0.720	99.0	1,0,0	U	47.1	-46.6
A2063A	230.77209	8.60918	10377	200	193	10312	667	1.350	142	10345	762	1.165	1.809	6.18	-0.069	-0.132	99.4	1,0,1	P	16.5	30.9
A2142	239.58345	27.23335	27254	232	191	26975	820	1.618	157	27036	828	1.767	2.157	11.10	-0.087	-0.276	66.7	1,0,1	P	41.0	200.0
A2147	240.57086	15.97451	10595	481	453	10929	918	1.858	397	10889	935	1.966	2.466	15.70	0.215	-0.286	100.0	2,2,0	M	119.9	-283.7
A2151	241.28754	17.72997	9378	331	311	10906	743	1.502	276	10898	768	1.551	1.999	8.35	-0.064	-0.573	100.0	3,2,2	M	3.1	-1466.6
A2152	241.37175	16.43579	13268	124	116	13283	398	0.799	64	13266	406	1.038	1.139	1.56	0.934	0.724	98.6	2,0,0	M	42.1	1.9
A2197	246.92114	40.92690	9511	294	276	9108	546	1.109	185	9114	573	1.402	1.593	4.21	0.258	-0.797	100.0	3,0,1	M	16.9	385.3
A2199	247.15948	39.55138	9296	521	498	9089	753	1.529	459	9090	779	1.302	1.907	7.21	-0.055	-0.058	100.0	1,0,3	P	6.4	199.9
A2204A	248.19540	5.57583	45528	111	96	45274	760	1.456	38	45497	1101	1.838	2.588	20.30	0.669	0.092	95.5	1,2,0	S	52.1	26.9
A2244	255.67697	34.06010	29543	106	102	29811	1154	2.282	102	29778	1161	1.491	2.546	18.30	0.166	-0.851	63.8	1,0,0	U	15.2	-213.8
A2256	256.11352	78.64056	17778	295	280	17567	1222	2.449	280	17567	1222	1.514	2.683	20.60	0.009	-0.624	99.9	1,2,2	S	129.2	199.3
A2255	258.11981	64.06070	22068	189	181	24100	992	1.973	179	24126	1000	1.802	2.470	16.40	-0.316	-0.518	100.0	1,2,0	S	183.7	-1904.7
A3716	312.98715	-52.62983	14112	157	140	13517	746	1.501	123	13508	783	1.247	1.878	6.99	0.168	-0.915	88.8	2,0,1	M	0.9	578.0
S0906	313.18576	-52.02746	13947	62	54	14481	340	0.680	26	14446	440	0.824	1.113	1.46	0.002	0.014	57.4	1,0,0	L	・ ・ ・	-476.1
A4012A	352.96231	-34.05553	16241	93	85	16219	473	0.947	39	16249	575	1.043	1.436	3.15	-0.126	0.431	73.1	1,0,0	L	・ ・ ・	-7.6
A2634	354.62244	27.03130	9117	192	185	9262	695	1.409	166	9268	717	1.251	1.780	5.87	-0.274	-0.177	94.9	1,1,0	S	51.7	-146.5
A4038A-49	356.93768	-28.14070	8672	247	237	8799	683	1.385	180	8873	753	1.150	1.789	5.95	0.252	-0.017	100.0	1,2,0	S	14.4	-195.2
A2670	358.55713	-10.41900	23157	308	288	22791	909	1.805	251	22799	970	1.153	2.089	9.91	0.066	-0.258	100.0	1,0,0	U	31.7	332.7

^a A capital letter after the ACO name indicates the line-of-sight component of the cluster (see ^{Chow-Martínez et al. 2014}). A symbol indicates the cluster center is not at the X-peak substructure. b Length and mass parameters are also in units of h ₇₀.

Note that some clusters in our sample do not have their ICM emission centered on the main structure of their clusters, but on a substructure (A0754, A1736B and A2151). These are marked with a ’x’ in the first column of the Table 3.

3.5. Gravitational Binding

For the 16 superposed clusters appearing in Table 2, as well as for the substructures reported in Table 8, we complemented our analysis by applying a test for gravitational binding. Since the evolutionary state of a system like a galaxy cluster is also related to its geometry in redshift space, any density enhancement present in real space will also appear as a density enhancement in redshift space: systems representing small overdensities, where the Hubble flow has not yet been significantly perturbed, appear essentially undistorted, while those that are clearly collapsing, the Hubble flow being slowed down, appear flattened along the LOS. On the other hand, systems that are close to virial equilibrium appear as particularly elongated condensations in redshift space, a phenomenon known in the literature as Fingers-of-God. Because of this effect, it is possible to assess what is the global dynamical state of a galaxy system at the scale of a cluster by evaluating its distortions in redshift space.

As explained by ^{Sargent & Turner (1977)}, this level of distortion can be determined, for a pair of objects (galaxies, groups or clusters), by determining the separation between the members of the pair and the angle χ between the separation vector and the plane of the sky. Such angle is measured as follows: let θ₁₂ be the angular separation between the center of the two galaxies, z ₁ and z ₂ (with z ₂ ≥ z ₁) being their respective redshifts, then the physical distance (d ₁₂) and projected separation (ℓ₁₂) in the plane of the sky are given, respectively, by:

and

the angle χ between the separation vector being equal to:

where 0 ≤ χ ≤ π/2.

For a homogeneous spherical system following the expansion flow, ⟨χ⟩ approaches the isotropic value of 32.7^o; ⟨χ⟩ tends to lower values for a collapsing (flattened) system and larger values for a virialized (elongated) one. Note, however, that for a non-spherical system, the geometrical elongation/flattening could dominate ⟨χ⟩, masking their real dynamical state.

Assuming a symmetric geometry, on the other hand, the same angle χ can be used to test the Newtonian criterion for gravitational binding of two systems (^{Beers et al. 1982}). This allows one to determine whether the pairs are either relaxed, collapsing or expanding, or not bound but simply close in space. Within the context of a two-body-problem, the orbits of the two galaxies or systems, with masses M ₁ and M ₂, are assumed to be linear, with no rotations or discontinuities around the center of mass. The projected separation between their centers would then be R _p = R cos χ (= ℓ₁₂) and their relative velocity projected along LOS, V _r = V sin χ, where R is the physical distance (= d ₁₂) between them and V is their relative velocity. Considering that the energy criterion for gravitational binding is, 12vesc2≤GMR where v _esc is the escape velocity, we assume V = v_esc and estimate the total mass to be M = M ₁ + M ₂, yielding the condition for the pair to be bound:

Having evaluated these parameters for the 16 cases of superposed clusters in our sample, we determined, as reported in Table 2, that 5 pairs and 2 clusters are only apparent superpositions.

3.6. CDG Related Parameters

CDG-X-ray offset: The offsets for 52 of the 59 clusters detected in X-rays in our sample were calculated based on the coordinates of the peak emission in X-ray compiled by ^{Piffaretti et al. (2011)}. However, for A2151 we did not use this source because the peak reported by these authors, although the brightest in this cluster, corresponds to the emission of a subcluster. Instead, we used the coordinates of the main structure as reported by ^{Tiwari & Singh (2021)}. For 5 of the 6 remaining clusters, the coordinates for the X-ray peaks came from three different studies (^{Ebeling et al. 1996}; ^{Ledlow et al. 2003}; ^{Sato et al. 2010}). This leaves one cluster, namely A0118, for which information is missing. The offsets, r _ox, reported in Column 21 of Table 3, correspond to the angular separations transformed into the physical separations in kpc at the redshift of each cluster.

To compare these offsets with those reported in the literature, we also calculated the relative offsets, using the relation:

Note that since ^{Piffaretti et al. (2011)} is our only source for r ₅₀₀, we only calculated Δr _ox for the 52 clusters in common with these authors (to be reported further in Table 5).

Consistent with a typical cooling time of 4 Gyr (see Figure 2 in ^{Zhang et al. 2011}), a cluster with an offset rox<30 h70-1 kpc, equivalent to Δr _ox ≲ 0.03, can be considered to be relaxed. Compared with the literature, this relaxation threshold is between two previously proposed values: ^{Lavoie et al. (2016)} used Δr _ox = 0.05 and ^{Lopes et al. (2018)} used Δr _ox = 0.01.

Peculiar velocity: We calculated the peculiar velocity of the CDGs using the formula (e.g., ^{Coziol et al. 2009}):

We also calculated the respective relative peculiar velocity using the definition (e.g., ^{Lauer et al. 2014}):

We report the values obtained for v _pec in Column 22 of Table 3, while Δv _pec is reported in Table 5. According to this parameter, we consider a system to be relaxed when |v _pec| < 175 km s⁻¹, which is equivalent to Δv _pec ≲ 0.21.

CDG luminosities: As described in § 2.3, we used the K _s absolute magnitudes of the CDGs, M _Ks, as a proxy for their stellar masses. Comparison of these masses with the masses (or number of galaxies) of the substructure hosting the CDGs can yield important information about the assembly histories of the clusters. In particular, one could expect the most massive CDGs to be located in the most massive substructures, and these massive substructures to form the main subclusters of their respective clusters. The absolute magnitudes of the CDGs are reported further in Table 5.

Magnitude gaps: Another important parameter relating the assembly history of the CDG to its cluster is its magnitude gap: assuming a CDG grows in mass by cannibalizing its neighbors, its magnitude gap is expected to increase with time. For our sample, we have calculated two gaps: (i) the difference in magnitude between the CDG and second-rank member, Δm ₁₂, and (ii) the difference in magnitude between the second and third-rank members, Δm ₂₃.

Note that when a CDG differs from the original BCG of the cluster (which is the case for 19% of the clusters in our sample, see § 3.1), the identification of the second-rank galaxy varies with the type of cluster: for both the Fornax-like clusters and clusters with a fossil candidate in their outskirts, the secondrank galaxy is the second-rank of the main structure, while in Coma-like cluster the second-rank is the initial BCG, brighter than the CDG; this produces a negative Δm ₁₂. The various gaps are also reported in Table 5.

4.1. Global Cluster Properties

Using the optical data related to galaxy membership, we show in Figure 4 the histograms characterizing the “global” properties of the clusters identified in Table 3. In the upper left panel, we show the distribution of r200, which is commonly used as a reference radius. The median of 1.35 h70-1 Mpc, corresponding to only 63% of the R _A, implies the galaxy concentrations in our sample of clusters are relatively high. In the upper right panel, the two distributions for the number of galaxies within the caustic, N _c, and galaxies within virial aperture radius, N _α , confirm this trend, the medians amounting to 150 and 114 galaxies, respectively. In the lower left panel, the distribution of redshifts is found to be positively skewed, since the mode appears before the median at z = 0.054. This shows that most of our clusters are nearby, and thus, assuming they formed in the distant past, had had enough time to virialize. Finally, in the lower right panel, the distribution for the velocity dispersion within 1.3 × r ₂₀₀ has a median value of 723 km s−1, which is typical for Abell clusters.

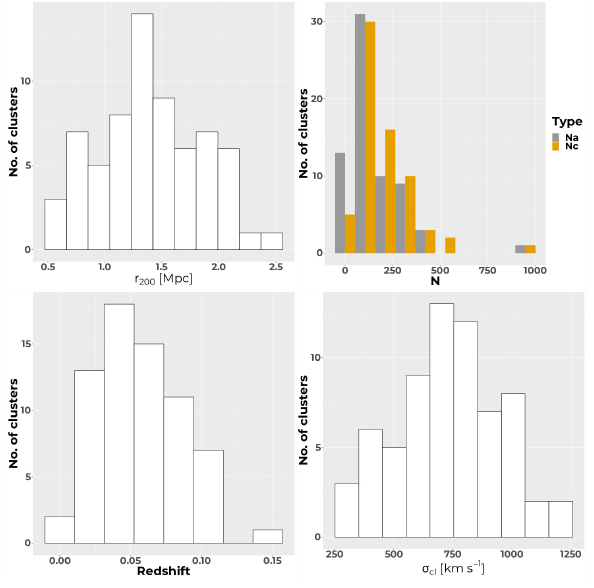
Fig. 4 Global properties of the clusters as defined in Table 3: Upper left, estimated r ₂₀₀ radii; upper right, number of galaxies within the caustics (N _c, orange) and within the virial radius (N _α, gray); lower left, redshifts; and lower right, velocity dispersions (σ_cl). The color figure can be viewed online. 

Based on the above distributions, we conclude that our sample is composed mostly of nearby, relatively rich clusters, where the concentrations of galaxy and velocity dispersion are remarkably high, justifying the assumption that those are systems that had had sufficient time to evolve internally and should then be expected to be close to virialization.

Consistent with this assumption, the distribution of the virial masses in the right panel of Figure 5 is found to be significantly negatively skewed, with a median 6.4 1014 h70-1 M⊙. However, the distribution for the virial radii, in the left panel, does not follow this trend, spannig a relatively large range, with a median value of 1.82 h70-1 Mpc, corresponding to 0.85 times the R _A. This peculiarity may suggest that the clusters either have different assembly states or even different assembly histories.

Fig. 5 Distributions of virial radius (left panel) and virial mass (right panel). 

Comparing our virial masses with those of the literature was not straightforward, since published estimates of these are rare. One suitable source is the GalWeight cluster catalog (GalWCat19; ^{Abdullah et al. 2020}), where the masses of 1 800 clusters were determined within three different projected radii: r ₁₀₀, r ₂₀₀ and r ₅₀₀. There are 18 clusters in this catalog that are also in our sample, and we compare, in Figure 6, their three different masses, M ₁₀₀, M ₂₀₀ and M ₅₀₀ with our M _vir estimate. The three linear fits we obtained are relatively good, with comparable correlation coefficients R ≈ 0.83, 0.87 and 0.89, respectively. However, since our virial masses were estimated using a proxy for r ₁₀₀ (cf. § 3.3), the comparison that counts for us is that with M ₁₀₀. In the lower panel, the fit shows our virial mass estimate to be in good agreement with those of GalWCat19 for r ₁₀₀, the residuals being due probably to the different ways the membership of galaxies in each cluster was determined, and the mean redshifts of galaxies in our data compared to only SDSS redshifts in theirs.

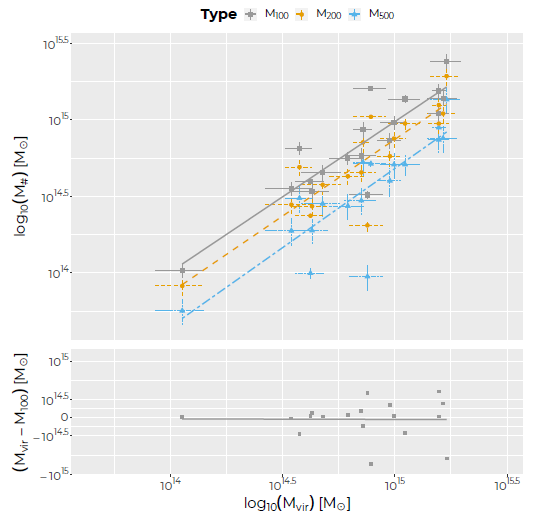
Fig. 6 Comparison of our mass estimates with the virial masses in the GalWeight galaxy cluster catalog. Blue triangles, M ₅₀₀, orange circles, M ₂₀₀ and gray squares M ₁₀₀. The three lines are linear fits to points with the same colors. In the lower panel, the residual corresponds to the comparison of our virial mass with M ₁₀₀. The color figure can be viewed online. 

To disentangle the assembly history of these clusters, we discuss in the following sections the implications of various dynamical parameters and classifications obtained for three different internal regions within the clusters. The three regions are the following: (i) the outer region, from R _vir down to r ₅₀₀, as traced by the optical data on galaxy membership; (ii) the inner region, inside r ₅₀₀, as traced by Xray emission; (iii) and the innermost core, characterized by gas cooling and CDG properties. Typical radii for these regions are Rvir ≈ 1.8 h70-1 Mpc, r500 ≈ 0.9 h70-1 Mpc and core radius (r _core) about 0.3 h70-1 Mpc (note that more specific values will be defined for the various radii as our analysis progresses).

4.2. Outer Region

The assembly state of the outer region is characterized by the presence or absence of substructures (cf. § 3.4). According to the DS-test, the 43 clusters with P _sub ≥ 90% in Column 18 of Table 3 could be considered to have substructures. This represents 64% of our cluster sample. However, considering all the results for the different tests, substructures appear to be secure in only 39 of these clusters and probable, with P _sub ≲ 90%, in 8 further clusters. In total, the number of clusters with substructures in our sample could thus be as high as 70%. Consequently, since either fraction is relatively high, it seems safe to conclude that substructures are extremely common in nearby clusters.

Taken at face value, the presence of numerous clusters with substructures suggests that many of these systems did not yet reach equilibrium, and what we observe, consequently, are different phases of a still ongoing process. To better characterize these different phases, it seems therefore important to first classify all the substructures in terms of their dynamical significance. This implies determining the gravitational impact that a substructure, when present, has on the whole cluster.

As a first approximation, this gravitational impact can be estimated by comparing the relative richness, N _s/N _c, formed by the ratio of the number of galaxies in each substructure, N _s, to the total number of galaxies within the caustics, N _c. Using the numbers in Table 8 of Appendix B, we distinguish three levels of dynamical significance:

Main (m): High relative richness, N _s/N _c ≥ 0.50. This level characterizes the dynamically dominant substructures in any cluster. In the case of multi-modal clusters (for example, A2804), the sum of the membership ratios of the main modes is indeed larger than 0.50. In Table 8, the substructures with this level of significance are identified by appending the suffix m to their ID.

Highly significant (hs): Intermediate relative richness, 0.05 ≤ N _s/N _c < 0.50. This level characterises substructures that are sufficiently massive to affect the dynamics of their host clusters. In Table 8 the suffixes (n, s, e, w, c, or a combination thereof) are added to the ID of the substructures indicating its location relative to the main structure (North, South, East, West or central, respectively).

Low-significance (ls): Low relative richness, N _s/N _c < 0.05. These are low-mass clumps of galaxies, attached to a more massive host cluster, that do not affect its dynamics. They are not listed in Table 8.

It is worth to note that the m substructure in our sample with the lowest value of N _s/N _c is A1736Am (0.581), while the hs substructure with the highest N _s/N _c is A3027Acw (0.235). Thus, the cut in N _s/N _c = 0.5 seems to be a good discriminator for this separation. The numbers of substructures with relative richness levels m, hs and ls are indicated in Column 19 of Table 3 using three numbers (m, hs, ls). For example, while A2798B and A2801 only have one main structure each, N _sub = (1, 0, 0), A2804, a bimodal cluster, has two, N _sub = (2, 0, 0). A more complex cluster is A0085A, which has one main structure, two hs and three ls substructures, N _sub = (1, 2, 3). A still more complex cluster is A2151, a trimodal cluster marked as N _sub = (3, 2, 2).

In Column 20 of Table 3 an extra parameter appears, A, which is used to qualify the “assembly state” of a cluster based on its level of substructuring. This classification was inspired by the morphological classifications of ICM X-ray emission proposed in ^{Buote & Tsai (1995)} and ^{Jones & Forman (1999)}. We distinguish five assembly states: highmass, Unimodal clusters (U); Low-mass unimodal (L); Multi-modal (M); Primary (P) with only ls substructures attached to the m mode; and finally Substructured (S), formed by the m mode and at least one hs substructure.

The way we distinguish between U and L clusters depends on the mass criterion 3.5 × 10¹⁴ M _⊙: U is more massive and L less massive or equal to this mass. In fact, the regular (unimodal) clusters may be either the “beginning” or the “end” of a merging process. They are the beginning if the poor clusters have had time to arrive close to relaxation, while in a relatively isolated environment. As the end, they are the final result of the virialization process of rich clusters. In fact there is no theoretical criterion justifying this distinction, and we chose pragmatically a threshold: the clusters for which we could see relatively relaxed X-ray isophotes were assumed to be close to virialization, while in the abscence of X-ray emission (implying a less dense or colder ICM, undetectable with ROSAT sensitivity, for example), we assumed the other state.

To be classified as M, a cluster must be formed by two or more m modes, with comparable richness. Consequently, in M clusters the CDG of the cluster is ill-defined, since there are different SDGs competing for this position (one for each mode, at least). For practicality, we choose as the CDG the SDG of the most central mode (usually the richest in galaxies and/or brightest in X-ray). This convention allows us to define a central position for the cluster and serves as reference for the magnitude gaps. Of the ten M-type clusters identified in Table 3, three, namely A0754, A2147 and A2152, show multiplicity only in the optical, while four, A1367, A2151, A2197 and A2804, show multiplicity in both optical and X-rays, and three others, A3356, A3395 and A3716, only in X-rays.

Finally, S and P clusters have both only one main structure and some substructures: in an S cluster there are hs substructures and in a P cluster they are all ls.

Adopting the above definitions, we count 21% U, 13% P, 42% S, 15% M and 9% L clusters. In terms of masses, Table 4 shows that U and P clusters are more massive than S and M clusters, while L clusters are the least massive of all. Thus, poor L clumps could represent the building blocks of future ’massive’ clusters. Also, the distribution in radii presented in Table 4 reveals that the “size” of a cluster and, most specifically, its virial radius increases with its mass.

Although 70% of the clusters (M, S and P) show some evidence of substructuring, considering the significance in terms of relative richness and mass, only 57% (M and S) are expected to be dynamically affected by their substructures. This implies that at least 57% of the clusters in our sample have not yet reached virialization. This may be compared to previous numbers reported for local cluster samples, e.g.^{Lopes et al. (2018)}, who found that substructuring ranges between 37-75%, in 40 SZ-detected clusters, and between 32-65%, in 62 X-ray clusters (both samples taken from ^{Andrade-Santos et al. 2017}). As a whole, for 31 clusters in common with these authors, our results agree for 80% of them.

How does this classification of substructures fit the model of cluster formation? According to the hierarchical model, clusters form mainly by the mergers of groups of galaxies. Within this paradigm U-type clusters would be examples of systems that merged in the distant past and their virialization process would thus be well advanced. P-type clusters would also have formed in the past and represent cases that, being massive, have recently attracted small groups in their environment without an important change in their relaxation state. This reinforces the idea that the cluster formation process is continuous. Consequently, clusters with significant substructures (M and S) would be examples of relatively more recent mergers (which occurred in the last 1-2 Gyr; ^{Lisker et al. 2018}; ^{Benavides et al. 2020}; ^{Haggar et al. 2023}). Their differences are explained by the importance of the merger: in S-type clusters a massive clump is accreting smaller mass groups (minor mergers), while in M-type clusters the masses of the merging entities are comparable (major mergers). Since average masses of M-type clusters are smaller, they could represent the previous step of the formation of the massive main clumps of S-type clusters. By comparing the sum of the merging masses (main + substructures) with the total mass of the cluster, in S clusters the merging masses are 7% less massive than the cluster mass (median 10%), compared to 23% (median 30%) in M clusters. Obviously, M clusters must be relatively less relaxed than S clusters.

The best examples of poor clusters might be the six L clusters. Indeed, the relatively low masses and small numbers of member galaxies in these systems make them comparable to groups. This might also explain why these poor clusters are not observed in X-ray: simply because they do not have sufficiently deep potential wells for infalling gas to heat up and emit detectable amounts of X-rays. This is the case of candidate AXU clusters like A0634 and A4012, for which confirmation should be obtained using eROSITA (Predehl et al. 2021). The four remaining L clusters also look like they could be either infalling or satellite groups of more massive clusters (see Table 2): these are the cases of S0334 related to A3104, S0336 related to A3112B, and possibly A3095 related to A3094A and S0906 related to A3716 (for which binding could not be established). Other infalling groups, composed by two clumps either and residing well inside the caustics of their main cluster are: A2870, related to A2877, and A4049, related to A4038. These cases would also be excellent candidates to search for evidence, in their galaxies’ properties, of pre-processing.

4.3. Inner Region

The region inside r ₅₀₀ is where the gas accumulates and gets very hot, emitting X-rays. In our sample, only eight clusters are undetected in X-rays (Table 1). However, quantitative information on ICM evolution is scarce and restricted to two parameters: dynamical status of the cluster ICM (71% of X-ray detected clusters) and core cooling status (81%). In Table 5 the values for these parameters in clusters with different A classes are reported in Columns 2 and 4, respectively. In Column 2, the symbol ✔ indicates a relaxed status while an ∗ indicates a disturbed ICM. The main sources for this information were ^{Parekh et al. (2015)} and ^{Laganá et al. (2019)}. In general, conclusions about the dynamical state of the inner region are confirmed by the different sources, except in four cases, the clusters A2029, A2052, A2063A and A2244, for which evidence of disturbance is still debated. In Column 3 of Table 5 we added information about the detected presence of radio halos and/or radio relics, mostly from ^{Van Weeren et al. (2019)}, ^{Knowles et al. (2022)} and ^{Botteon et al. (2022)}. For the 4 cases above, these data indicate disturbance for A2029, A2063A and A2244, and no information concerning diffuse radio emission for A2052. In general, the presence of radio halos and/or relics coincides with the disturbed status of the ICM X-ray data (except for two substructured clusters, A0133A and A1656).

Although the cooling state is related to the core of the clusters, we will discuss it here, together with the remaining X-ray information. In Column 4 of Table 5, the core cooling status is codified as follows (see, for example, ^{Käfer et al. 2019}): strong-coolcores (SCC), which have cooling times t _cool < 1 Gyr and usually show a temperature drop towards the center and small core radii (< 100 kpc; e.g., ^{Ota et al. 2006}); non-cool-cores (NCC), with t _cool > 7.7 Gyr (see also ^{Hudson et al. 2010}), with flat central temperature profiles and large core radii; and weak cool-cores (WCC), with intermediate characteristics (although sometimes also classified as cool-cores). In some clusters the index ‘s’ is also added when “sloshing” (the presence of spiral-shaped central cold fronts) is observed. In terms of assembly state, clusters with SCC or WCC are expected to be closer to relaxation, that is, they had enough time to settle, and radiatively cool. NCC clusters, on the other hand, are likely to be younger, or disturbed due to recent mergers, or even re-heated by AGN feedback. Finally, evidence of sloshing in these cores might suggest more recent accretion.

How do these classifications in X-ray fit our general interpretation based on the assembly classes, U, P, S and M? The best agreement is for the M class: 9 out of 9 clusters in Table 5 are considered disturbed according to the X-ray emission (Column 2), while 5 are NCC and 1 is WCC (Column 4) of a total of 6 with this information. Although the situation is more complex for the S and P clusters, the agreement is also relatively good. For the S-type clusters, 11 out of 17 are considered disturbed based on the X-ray distribution, while 11 are NCC, 4 are WCC and only 7 are SCC. However, considering the evidence of sloshing in five of the SCC, as much as 20 out of 22 S-type clusters could be considered to have a non-relaxed ICM. Note that the diagnostics based on X-ray distribution and core temperature differ in five cases, the ambiguity increasing for the WCC and SCC. This ambiguity appears clearer in the P-type clusters: although 7 out of 7 have non-relaxed ICM, 5 out of 9 are WCC and 4 are SCC with sloshing. Considering their particular assembly state histories -these are old and massive clusters accreting smaller mass systems- some level of ambiguity in the core cooling status might naturally be expected. The U class, however, is definitely the most surprising. Although we expect all of these clusters to be close to relaxation based on the X-ray distribution, only 2 out of 9 seem to be, 5 are suggested to be disturbed and 2 are ambiguous. The core cooling states draw a similar complex picture: 4 are NCC (usually also disturbed), 5 are WCC (one with sloshing), and 2 are SCC (also one with sloshing). This is relatively unexpected, since most of our U-type clusters lying at low redshifts should have had time to reach relaxation through interactions.

However, the fact that very few clusters are classified as U, combined with the “unusual” characteristics of their inner regions compared to their outer region (absence of substructures), suggest that the process of virialization, even in the most evolved systems, does not depend solely on time but also on complex processes involved in their assembly history. Merging can happen anytime in the history of a cluster -possibly taking it out of a previous equilibrium situation. Also, merging of major and minor subclusters has different consequences, and the same applies to different ICM properties. Thus, different regions sampled by optical and X-ray observation may show distinct moments of this assembly history. In fact, this could explain the frequent disagreement between optical and X-ray results concerning the dynamical state of galaxy clusters.

4.4. Core Region

In this innermost region, the most relevant feature is the CDG, and possibly other dominant galaxies. Consistent with its definition, the CDG position in a cluster is expected to indicate its dynamical center. This is also the expectation for the X-ray emission peak (or centroid), although the two components, galaxies and gas, may be subject to different levels of disturbance with respect to the global potential well, dominated by dark matter. This is why the dynamical status of the CDG, with respect to the gas distribution and to the radial velocity distribution of galaxies, is an important information to compare with the assembly status discussed above.

In the left panel of Figure 7, the distribution of Δr _ox for the total sample is shown, with an assumed upper threshold for relaxed CDGs, Δr _ox = 0.03, marked as a yellow vertical line. We see that 55% of the clusters (29 out of 53) are well above the threshold. The median for Δr _ox is 0.04 or about rox = 40 h70-1 kpc. This suggests that more than half of the clusters in our sample have a non-relaxed CDGs.

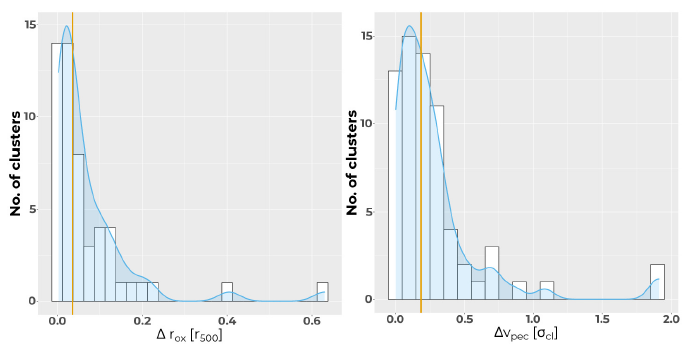
Fig. 7 Left: Distribution of the relative projected positional offset of CDGs with respect to the X-ray peak (Δr _ox). Right: distribution of the relative peculiar velocity of CDGs with respect to the cluster systemic velocity (Δv _pec). The vertical yellow lines in the two panels are the thresholds separating relaxed form non-relaxed clusters. The color figure can be viewed online 

In the right panel of Figure 7, we trace the distribution for Δv _pec. By definition of the CDG, in a dynamically relaxed system one would expect Δv _pec to tend to zero. However, assuming a typical upper threshold Δv _pec = 0.21, the percentage of clusters that have higher values is as high as 46% (31 out of 67). With a median Δv _pec = 0.185 σ_cl, corresponding to a median v _pec of ± 147 km s−1, once again it is clear that a large number of clusters cannot be assumed to have relaxed CDGs.

Note that, compared with the literature (e.g., ^{Coziol et al. 2009}; ^{Lauer et al. 2014}; ^{Lopes et al. 2018}), our median value for Δv _pec is relatively low. This is not due to a difference in sample but rather to a difference in the identification of the CDG. For example, in the cluster A2197, ^{Lauer et al. (2014)} assumed NGC6173 is the BCG, instead of NGC6160, which we identified as the real CDG. Since NGC6173 turned out to be the SDG of a substructure of A2197 (A2197me in Appendix B), its v _pec is naturally estimated to be larger than for NGC6160. This emphasizes that a thorough analysis of the substructures in clusters is necessary to better determine the assembly state of the clusters. However, despite our careful analysis, the upgraded cluster peculiar velocities and velocity dispersions, we must still conclude that a significantly large number of nearby clusters do not have a relaxed core.

In fact, considering the clusters individually or in any of the assembly state class, we found no correlation between Δr _ox and Δv _pec, as can be seen in Figure 8 (compare, also, Column 21 with Column 22 of Table 3), a fact already noted in the literature (e.g., ^{Lauer et al. 2014}; ^{De Propris et al. 2021}). This advocates against the use of only one of these parameters as the proxy for the shift from the bottom of the cluster potential well, as proposed by, e.g., ^{Lopes et al. (2018)}. In the present work we consider both together as indicators of the displacement of the CDG with respect to the bottom of the cluster potential well. Thus, we find that 70% of the clusters in our sample present significant disturbances in their mere core. The parameters Δr _ox and Δv _pec are reported respectively in Columns 5 and 6 of Table 5. In Column 7, both offsets are used to classify the state of the CDG, adopting the same code as for Column 2, that is, the mark ∗ is assigned when any of them indicates dynamical disturbance.

Fig. 8 Distribution of offsets, parameterized. The color figure can be viewed online. 

To obtain a more comprehensive view of the impact of substructures, we show in Figure 9 violin plots for Δr _ox and Δv _pec, for each class of assembly state. In the upper left panel (Δr _ox), the only trend visible is for the CDGs in the P class to lie below the threshold. This is confirmed for the pairs (U,P) and (P,S), a difference in the distribution being found using a Mann-Withney test at 95% CL, with P = 0.008 and P = 0.025, respectively. However, a Kruskal-Wallis test performed comparing the whole classes (with Dunn’s post-tests) found no statictically significant differences. Similarly, a Kruskal-Wallis test for Δv _pec, in the upper right panel, was also negative, with P = 0.512. Thus, we see no evidence for Δrox and Δv _pec to be related to the classes of assembly state.

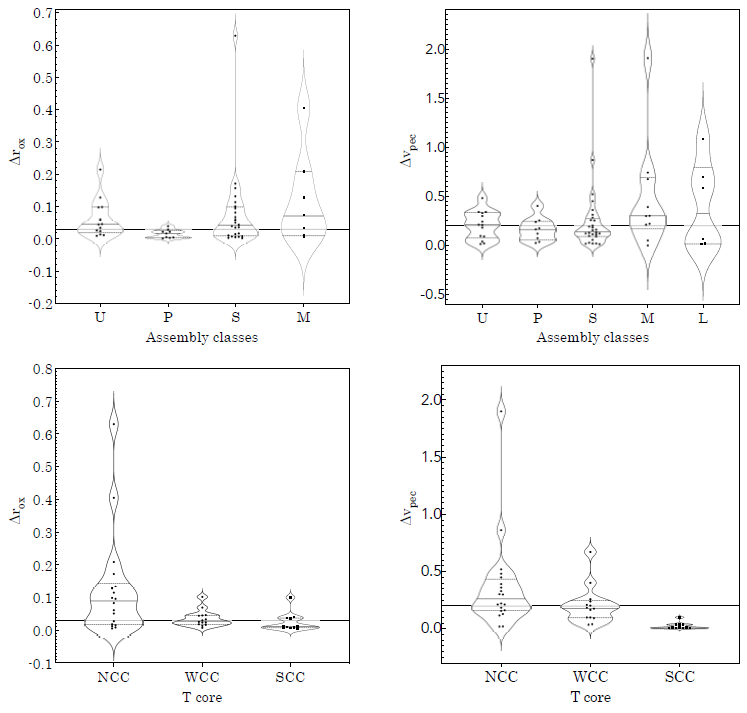
Fig. 9 Distributions of CDG parameters in different assembly classes (upper panel) and different core cooling status (lower panel): Left panels, Δr _ox, right panels, Δv _pec. In each graphic, the threshold for relaxation associated to the parameter is shown as a horizontal line. 

In the lower panels of Figure 9, we compare the distribution of Δr _ox (left) and Δv _pec (right) separating the clusters based on the core cooling status. Performing a Kruskal-Wallis test for Δr _ox, we find a statistically significant difference between the NCC and SCC (with P = 0.011) but not between NCC and WCC or WCC and SCC. However, for Δv _pec the difference is much more significant (P ≪ 0.0001) between both NCC and SCC and WCC and SCC (but no difference between NCC and WCC as before). We find a 60% probability for WCC and NCC clusters to be associated with clusters that have both high Δr _ox and Δv _pec, the trends being more obvious in S and M clusters than in U and P clusters. Considering that the latter two classes represent more massive clusters than the two former ones (cf. Table 4), the U and P clusters, consequently, are possibly slightly more relaxed than the S and M clusters. This is consistent with the complex assembly history of the clusters suggested by the assembly state classes. This correlation has already been pointed out in the literature: ^{Zhang et al. (2011)}, for instance, found that the CDG-X-ray offset is related to the central cooling time of the clusters, for the HIFLUGCS X-ray flux limited galaxy cluster sample, suggesting that the system must be close to relaxed to have its cooling flow enhanced, or a CC formed.

In general, the fact that the probability of association between the parameters related to the galaxies and gas in the core is not higher than 60% suggests that these two components most probably follow different paths towards equilibrium, the virialization time-scale, most specifically, being much smaller for the gas than for galaxies.

4.5. Results on the Co-Evolution of CDGs and Clusters

The remaining columns in Table 5 are dedicated to report the evolutionary parameters for the CDGs: the magnitude gaps Δm ₁₂ (Column 8) and Δm ₂₃ (Column 10); the projected separation (clustercentric distance) of the 2^nd-rank, Δr ₁₂, and 3rdrank, Δr ₁₃ (Columns 9 and 11, respectively); and additional comments in Column 12.

Using MKs as a proxy for the stellar mass of the CDG (e.g., ^{Schneider, Gunn & Hoessel 1983}), we traced in the left panel of Figure 10 its distribution for all the CDGs in our sample. A relatively good Gaussian fit suggests some level of similarity in the evolution of these CDGs. However, the distribution of the magnitude gaps, Δm ₁₂, in the right panel of Figure 10, is clearly bimodal, indicating different assembly histories for the CDGs themselves.

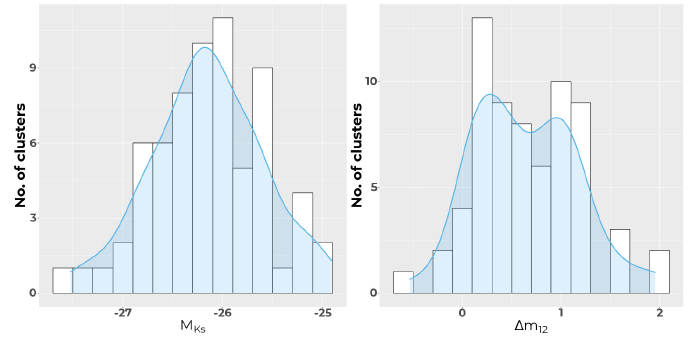
Fig. 10 Distributions of CDGs properties: Left panel, CDG MKs, right panel, Δm ₁₂. The color figure can be viewed online. 

This can also be appreciated in Figure 11, which shows the distribution of absolute magnitudes for the CDGs and their respective second-rank galaxies as a function of the magnitude gaps Δm ₁₂. As the gap increases, the luminosity of the CDG (its mass) grows almost linearly, while the luminosity of the secondrank galaxy slowly declines. Note that, due to our thorough analysis of substructures and definition of CDGs, it is not surprising that the change in mass we find is much faster than what was seen before (e.g., ^{Smith et al. 2010}). Although systems showing large magnitude gaps are consistent with a model where the CDG co-evolve with its cluster, the bimodality clearly suggests more complex assembly histories for the CDGs.

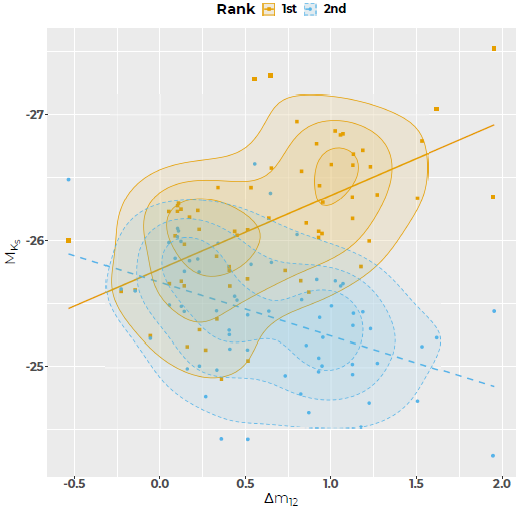
Fig. 11 Distributions of absolute magnitudes for CDGs and 2^nd-rank galaxies as function of the magnitude gap. The color figure can be viewed online. 

To shed more light on the co-evolution of the CDGs and their clusters, we compare how the two magnitude gaps, Δm ₁₂ and Δm ₂₃, vary in the different assembly classes. This is done in the upper panels of Figure 12. Although there is an apparent trend for U and P clusters to have larger magnitude gaps between the CDG and second-rank galaxy than for the S and M clusters, a Kruskal-Wallis test found no statistically significant difference (P = 0.190). Similarly, a Kruskal-Wallis test found no statistically significant difference (P = 0.125) for Δm ₂₃.

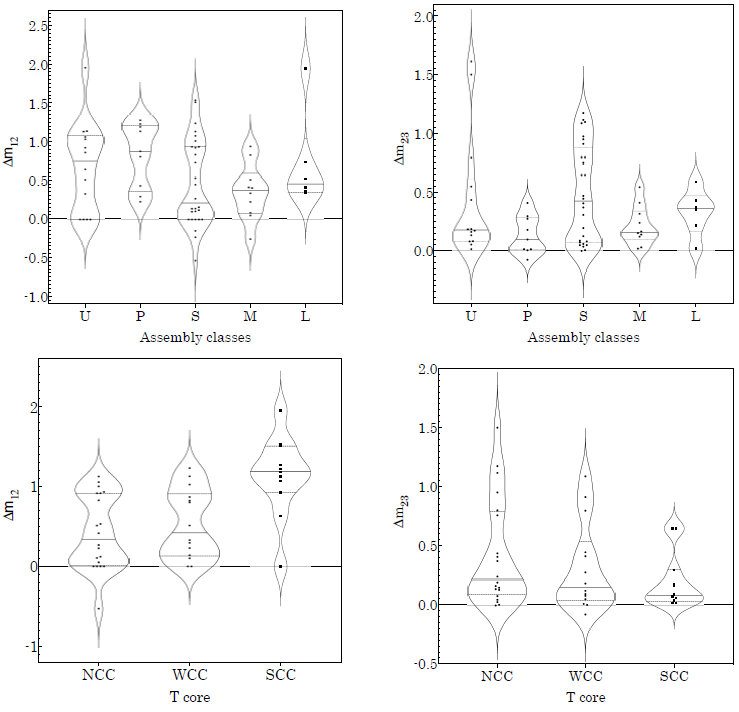
Fig. 12 Comparison of magnitude gaps in different assembly classes (upper panels and cooling states (lower panels). 

In the lower panels of Figure 12 we compare the two magnitude gaps for the different core cooling states. This time the Kruskal-Wallis test clearly identified a statistically significant difference for Δm ₁₂, with P = 0.002, between the pairs (NCC, SCC) and (WCC, SCC), but not for Δm ₂₃. This is consistent with what we found before for Δr _ox and Δv _pec. Consequenlty, despite the clear evidence of co-evolution of the clusters and their CDGs, especially in the core, the fact that the assembly state classes contain a mixture of core cooling states seems to confirm the complex assembly history of clusters in general.