SARS-CoV-2 contagium analysis
The rapid global spread of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) causing the coronavirus disease COVID-19 set out a tremendous amount of research for development of control and mitigation measures of the disease in affected regions. Therewith, several epidemiological concepts have been key to the understanding of the virus transmission and spread and, with it, planning for intervention (Li et al., 2021). Among those concepts are the serial interval, SI: the period between symptom onset of an infector and an infectee, and the generation interval, GI: the time between infection events in an infector-infectee pair (Lehtinen et al., 2021). The SI has proven to be an indicator for effective epidemic surveillance and is a proxy to GI estimation. The GI is essential to estimation of the basic reproductive number, that is, the average number of individuals infected by a single infector in a susceptible population (Rothman et al., 2013). Both the SI and GI are the basis in epidemiological models aiming at guiding infectious disease intervention strategies (Ganyani et al., 2020).
In this review, we examined the relevance of the SI and GI to the understanding of the dynamics of two important citrus diseases: tristeza virus and Huanglongbing (HLB). La tristeza is a disease caused by a phloem-limited virus (CTV) of the family Closteroviridae, genus Closterovirus, which infects citrus and related species (Dawson et al., 2013). HLB, previously referred to as citrus greening disease, is one of the most destructive diseases of citrus worldwide caused by at least three species of the phloem-limited bacterium Candidatus Liberibacter (Bové, 2006). These diseases are the most prominent problems to production of citrus in Mexico and other citrus-growing regions of the world, where they have killed millions of citrus trees (Moreno et al., 2008; Gottwald et al., 2007; Spreen et al., 2014; Dawson et al., 2015; Dala-Paula et al., 2019). Both diseases are vector-borne, with CTV transmitted primarily by the brown aphid Toxopera citricida and CLas by Diaphorina citri.
Like SARS-CoV-2, CTV and CLas exhibit a period of transmission in which diseased individuals manifest no symptoms, yet are already contagious (Lee et al., 2015; Moreno et al., 2008). Spread of CTV and CLas during such asymptomatic phase, however, is still poorly understood through usage of traditional epidemiological parameters such as disease infection rates, area under the disease progress curve, and dispersal distances. In contrast, early transmission dynamics of COVID-19 have been accurately characterized using the SI and GI as epidemiological measures (Ganyani et al., 2020; Ferretti et al., 2020; Lehtinen et al., 2021; Li et al. 2021; Mettler et al., 2020; Ng et al., 2021). The objective of this review is to discuss the meaning of the SI and GI to put into perspective their potential usefulness or lack thereof in enhancing our understanding of the epidemiology of CTV and HLB. We discuss approaches to identification of infector-infectee tree pairs, which would be an important step in the SI and GI determination; we also discuss the estimation of the intervals and their distribution for both diseases. It is envisaged that this review motivates discussions on estimation and usage of these concepts to enhance understanding of the epidemiology of both of the herein examined citrus diseases.
Serial and generation intervals applications
Definitions. The serial interval (SI) and the generation interval (GI, also referred to as the generation time) are key epidemiological parameters used in public health to characterize the transmission dynamics of diseases such as COVID-19 (Ganyani et al., 2020; Ferretti et al., 2020; Li et al. 2021; Mettler et al., 2020; Ng et al., 2021; Lethtinen et al., 2021). The SI implies the time difference between symptom onset of an infector and an infectee, whereas the GI implies the time difference between being infected and infecting others or the time between infection events in an infector-infectee pair (Figure 1) (Lehtinen et al., 2021). Other concepts that are used in the study of infectious diseases are the basic reproductive number (R0) and the incubation period. The basic reproductive number, a measure of the transmission potential of a disease, quantifies the average number of secondary infections produced by a typical case of an infection in a population of all susceptible individuals (Rothman et al., 2013). The incubation period (IP) is the elapsed time from infection to symptom onset. In plant pathology, the IP is defined as the time between infection by a pathogen and the onset of symptom expression in the host plant. Latency or latent period is defined for viral diseases or for diseases caused by fastidious bacteria similar to viruses, as the time between a tree infection and the onset of infectivity. For crop diseases, the incubation and latent periods begin at infection and are related temporal processes (Agrios, 2005). In both humans and plants, newly infected asymptomatic individuals will initially remain in their latent period and do not transmit the pathogen (Leung et al., 2018). However, when the GI is fulfilled, asymptomatic individuals can become infective and transmit the causative agent of the disease (Gottwald et al., 2002; Rimbaud et al., 2015; Qian et al., 2020; Johansson et al., 2021). By definition, latency ends when infectivity begins. Generally, the incubation period is longer than the latent period. Unlike the infection process caused by the SARS-CoV-2 virus strain directly between humans, viral and bacterial infections in trees are often transmitted between fruit trees by an insect vector. Thus, in the latter case, transmission is not direct, but depends on variables that affect the biology and ecology of the vector (Gottwald et al., 1999; Canale et al., 2017). Assessing or determining the incubation and latent periods for vector-borne diseases remains a challenge (Rimbaud et al., 2015).
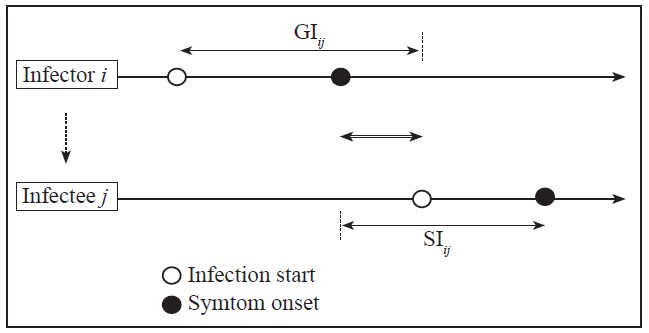
Figure 1 Representation of the serial interval (SIij) and the generation interval or generation time (GIij) in an infector i-infectee j COVID-19 transmission chain. Hollow arrow in the middle represents the time length from symptom onset of i to infection of j. The incubation period (not indicated) is the time from start of infection (white circle) to symptom onset (black circle) in each individual. Based on Lehtinen et al. (2021).
Transmission chain of the examined diseases
COVID-19. The COVID-19 is an infectious disease caused by a newly identified Coronavirus (Coronaviridae: Beta-coronavirus), an enveloped, positive single-stranded RNA virus with the characteristic “crown-like” spikes on its surface. The first case was identified in Wuhan, China, in December 2019 (Asselah et al., 2021). Symptoms of the disease can be described as mild in most people, although it can also cause severe illness and even death in others (Mavrodiev et al., 2020; Wu et al., 2020). The chain of infection of COVID-19, as defined in public health, refers to the series of interconnected stages since an infectious agent leaves its host, is conveyed by some mode of transmission, until it enters and infects a new susceptible host. The chain of infection of COVID-19 has an exponential phase, as infected and healthy hosts get within a close-range distance thus favoring direct or indirect transmission (Wu et al., 2020). Direct transmission can occur through kissing or sharing eating utensils, whereas indirect transmission occurs by touching a surface contaminated by virus-containing secretions and then touching a portal of entry such as eyes, nose or mouth. Another form of COVID-19 transmission occurs when virus-containing droplets and aerosols are expelled from an infected person through speaking, breathing, coughing and sneezing (Prather et al., 2020). The transmission chain begins when a symptomatic or asymptomatic infector or primary source infects one or several individuals (infectees) who are in proximity (Qian et al., 2020; Wei et al., 2020). This pattern is affected by the mobility of and exposure to symptomatic or asymptomatic infectors. Pre-symptomatic transmission occurs when the GI is shorter than the IP of the infector. According to Nishiura et al. (2020) the median SI is shorter than the median IP, suggesting a substantial proportion of pre-symptomatic transmission. In other study it was estimated that at least 50% of new SARS-CoV-2 infections originated from exposure to individuals with asymptomatic infection (Johansson et al., 2021). For this reason, mitigation measures such as quarantines, social distancing, mask use, hand hygiene and strategic qPCR testing of people help reduce the risk of transmission, thus interrupt infection chains as early as possible.
The duration of the SI and GI of COVID-19 is estimated from contact-tracing data in a transmission chain from confirmed cases (Ganyani et al., 2020; Ferretti et al., 2020; Li et al. 2021; Mettler et al., 2020; Ng et al., 2021). Estimates suggest a SI mean of 7.5 days (95% CI: 5.3-19), GI mean of 3.95 days (95% CI: 3.01-4.91), and IP mean of 5.2 days (95% CI: 4.1-7.0) (Ganyani et al., 2020; Li et al. 2020). In the transmission chain of COVID-19, the length of the SI is affected by the infector-infectee interaction, as the pair may include persons of different age and response to COVID-19 infection. For instance, it has been observed that while some people exhibit only very mild symptoms, others may express a highly severe syndrome or die.
Citrus tristeza virus (CTV). In plant disease epidemiology, the term “transmission chain” is not of common usage. Instead, the chain of infection of a disease is better referred to as the disease cycle, which refers to the different events that are conducive to disease in a portion of or in an entire plant population (Agrios, 2005). CTV is not transmitted by seed. Long-distance spread is mainly by transport of asymptomatic infected plant material by man. Thus, in newly established citrus orchards, the primary source of CTV inoculum is often the infected planted material. Once introduced into a citrus grove, short-range or local spread within orchards or groves is carried out by insect vectors (aphids). From infected trees, CTV is acquired by aphid populations that are responsible for secondary spread. Several species of aphids transmit CTV (Lee et al. 1994; Yokomi et al. 1994), of which Aphis citricidus (Syn. Toxoptera citricida) is the most efficient vector of CTV and transmits the virus in a semipersistent manner (Gottwald et al., 1998; Dawson et al., 2013). The acquisition requires a feeding period of 4-6 hours and aphids remain viruliferous for 24-48 hours without undergoing a latent period (Rocha-Peña et al., 1994). The transmission chain of CTV can be simply described as: primary source/primary inoculum dispersion/first infected tree in an orchard → acquisition of the virus by an aviruliferous aphid → transmission of the virus by the aphid to a healthy tree → transmission to another healthy tree and → end of the transmission chain in 30 days with the end of the vector life cycle. Increase in the number of infective vectors in a population (increased secondary inoculum/transmission) → increase in the number of trees infected. In a transmission study conducted in the Yucatan Peninsula in Mexico, a transmission range of A. citricidus of 0 - 14.8% was estimated depending on the origin of the CTV isolates (Hernandez, 2013). The epidemiological implication of these biological characteristics is reflected in high rates of temporal dispersion of CTV in field conditions (Rivas-Valencia et al., 2017). For example, in Mexico, the incidence of CTV diseased trees increased 40% in a period of four years. Dispersal of severe isolates is increased by A. citricidus, even in rootstocks considered tolerant to CTV (Rivas-Valencia et al., 2020).
Usually, CTV has an incubation period that lasts for several years, as citrus trees decline suddenly years after infection (Fishman et al., 1983). This is commonly called a chronic infection. The disease, in endemic regions is present in more than 90% of citrus producing trees in an asymptomatic condition (Mora-Aguilera, 2008; Mora-Aguilera et al., 2005; Rivas-Valencia et al., 2017). In order to detect trees infected with CTV (asymptomatic or symptomatic), plant tissue is sampled and serological (ELISA) or molecular (RT-PCR) diagnostic techniques are applied (Hughes and Gottwald, 1998; Huang et al., 2004; Rosa et al., 2007; Ruiz-Ruiz et al., 2007; Korkmaz et al., 2008; Saponari et al., 2008). There are few studies on the incubation periods of CTV. Balaraman and Ramakrishnan (1979) experimentally determined that a 100% transmission of the virus was only achieved with at least 15 viruliferous T. citricida feeding on one plant and that the aphids required 24 h for each period of acquisition and transmission. The incubation period was reduced by 15-20 days when more than 100 aphids were feeding per plant. In another experiment, a decline isolate inoculated in sour orange seedlings remained for 51 days in the basal parts of the plants but was systemically distributed throughout the plant by 58 days post inoculation (Rocha-Peña et al., 1994). Gottwald et al. (2002) determined that CTV inoculated either in the spring or in the fall in 2-3 year-old trees, remain serologically undetectable until the following spring or later. Even during the following spring only some of the trees may have detectable infections. They figured out that systemic movement of CTV occurs within a few weeks after inoculation, but the detection threshold (the amount of virus load) remained quite low. Therefore, there is a considerable variation in latent period between initial and systemic infection.
Huanglongbing (HLB). HLB is one of the most serious problems of citrus worldwide. HLB is caused by Candidatus Liberibacter spp., a fastidious phloem-restricted bacterium transmitted by leafhoppers, and is characterized by a long incubation period of three months to multiple years before symptoms are visible (Manjunath et al., 2008; Flores-Sánchez et al., 2017; Canale et al., 2020). The Asian psyllid Diaphorina citri is the most efficient vector and transmits the pathogen in a circulative-propagative (persistent) transmission cycle (Manjunath et al., 2008; Hall et al., 2013; Torres-Pacheco et al., 2013; Keremane et al., 2015; Galdeano et al., 2020). According to Canale et al. (2017), the psyllids were able to transmit the pathogen for up to 5 weeks after a 14-day acquisition access period as nymphs. The psyllid is capable of acquiring the pathogen after feeding for 15 to 30 minutes and remains infective throughout their life (3 to 4 months) (Hall et al., 2013; Galdeano et al., 2020); transovarian transmission has been reported only in the African psyllid Trioza erytreae (Manjunath et al., 2008). Gottwald et al. (2008) analyzed the effect of contagion by psyllids at close range, on the global dispersal pattern of the disease over time, finding that the infection of trees occurs mainly by psyllids that come from contaminated tree blocks not close to uninfected trees, and not by psyllids from nearby orchards. Studies conducted in citrus orchards in Florida on the spatial distribution of HLB, evidenced the existence of two infection processes (Gottwald et al. 2008): a process of primary dispersion, where contagion occurs mainly by long-distance vector transmission, and another by local dispersion that occurs within the orchard. The authors concluded that the most devastating contagion is associated with vectors coming from long distances, regardless of local control carried out with insecticides, since psyllids fed the distant trees (detected as infected with CLas) will continue to infect local orchards before dying from insecticide applications. The transmission chain of CLas can simply be described as: primary source or first infected tree → acquisition of the bacterium by a non-infective Diaphorina → transmission to a healthy tree and so forth.
Several researchers have reported variable incubation periods for CLas, from a few months to one or more years (Gottwald et al., 1989; Gottwald, 2010; Canale et al., 2020). It has also been reported that in younger orchards the pathogen has incubation periods from 6 to 12 months. In a study by Irey et al. (2006), RT-PCR detection revealed that 50% of infected trees were symptomatic and 50% asymptomatic. In practice it is assumed that there can be two to manyfold more asymptomatic infections already established compared to those that are visually symptomatic in a given orchard. Thus, visual detection of HLB is inadequate because it leads to an underestimation of disease amount (false negatives). Further, systemic distribution within trees is incomplete or diffuse making early detection by molecular techniques even more difficult (Gottwald et al., 2008). This is the reason why CLas is highly invasive when introduced to new areas, i.e., the disease is usually highly spatially dispersed regionally prior to symptom expression (owing to the prolonged incubation period).
The prolonged incubation period and a regional dispersal can make eradication efforts nonviable (Gottwald, 2010). Recently, the median latent period was estimated to be 16.8 and 17.8 days for nymphs and adults of the psyllids that acquired the pathogen, respectively (Canale et al., 2017).
Estimation of the CTV and CLas serial and generation intervals and their distributions
In the estimation of the SI and GI for COVID-19, infector-infectee pairs are normally constructed ex post facto from contact-tracing data of infected cases from official public records. Then, a number of transmission chains is determined from those data and the obtained measurements for SI are used to estimate the GI distribution using mathematical or statistical models through frequentist or Bayesian approaches (Li et al., 2021; te Beest et al., 2013). Estimation of the intervals for CTV and CLas can be more challenging because it should consider the indirect mode of pathogen acquisition and transmission by their mobile vectors and the sessile nature of the citrus trees. The latter condition can be advantageous for identification of infector-infectee tree pairs within orchards, however, provided the disease and vector population are monitored both spatially and temporally. An approach to pair assignation can be the examination of incidence maps of tristeza or HLB from periodic assessments, followed by spatial autocorrelation analysis of incidence data to determine the presence or absence of aggregation of diseased trees and, if aggregation is detected, its directionality and intensity too. The degree of spatial dependence indicated by the number of spatial lags with significant correlations (p<0.05) could be used to guide identification of trees in the incidence map as the possible infector-infectee pairs. Significant correlations at first, second or third order could be considered to account for the vector dispersal distance (Kobori et al., 2011; Loxdale et al., 1993) and the citrus row and tree spacing commonly used in commercial orchards. Monte Carlo simulation (an example is given in Table 1) and Markov-chain Monte Carlo Methods can be used as an alternative to spatial autocorrelation to estimate randomness or lack thereof of diseased trees within an orchard. In the example provided in table 1, the observed distance between 12 diseased trees and their first nearest neighbor in a Persian lime orchard was 7.13, whereas the estimated distance from the randomization test (from 1000 simulations) was 7.1552. The difference was 0.0252. This means that the probability of a value as far as or farther than 7.13 is from 7.1552 is estimated as the proportion of the 1000 values that are 7.13 or less or 7.1804 (from 7.1552 + 0.252) or more. There are 496 values this extreme, so the significance of the results is estimated 0.496. This suggest evidence that the arrangement of the diseased trees in the orchard was random. Markov-Chain Monte Carlo Methods can also be used directly to identify infector-infectee tree pairs. In addition, as long as the event independence assumption is met, conditional probability and Bayes’ theorem can be used to estimate the probability that a given tree was the infector to its nearest first, second or third neighbor. Explicitly, the probability that a symptomatic tree A be the infector of tree B given that B is its nearest neighbor [P(A|B)] would be estimated by the probability of tree B being the infectee given that the symptomatic tree A is a primary source tree for infection to its closest neighbor [P(B|A)], multiplied by the probability of B and divided by the probability of B. The equation form is: P(A|B) = [P(B|A) P(B)] / P(B), where: P(A) is the probability of a symptomatic citrus tree A be a primary source tree or infector to its closest neighbor, and P(B) is the probability of a symptomatic tree B being the infectee by tree A assuming that it is its closest neighbor and was asymptomatic before A.
Table 1 Observed distances (m) between 12 HLB-diseased Persian lime trees and their four nearest neighbors in a 180-tree orchard, the estimated mean distances from 1000 randomly generated data using Monte Carlo simulation, and the estimated significance levels of the observed values.
| Distance (m) | 1st nearest neighbor | 2nd nearest neighbor | 3rd nearest neighbor | 4th nearest neighbor |
|---|---|---|---|---|
| Observed | 7.13 | 9.78 | 14.52 | 17.19 |
| Estimated Mean | 7.1552 | 9.7746 | 14.5525 | 17.2107 |
| Significancez | 0.4961 | 0.5040 | 0.5001 | 0.4986 |
zThe significance level for each i th neighbor is the estimated probability of getting a value as high as the one observed, which is interpreted as the probability of a value as far as or farther from the mean of the simulated distribution.
Data were obtained from an HLB study carried out in the north central region of Veracruz, Mexico from 2019 to 2020 (Dominguez et al., unpublished) and data were simulated in R
Distribution of the serial and generation interval of CTV and CLAS can be estimated with the observed SI data from the previous steps using similar approaches as those for COVID-19 (Lehntine et al., 2021). Since the SI can take a continuum of values and be negative (shorter than the incubation period) then it requires a probability distribution model for a continuous random variable and that admits negative values. The lognormal, Gamma and Weibull distributions are suggested as variable distribution choices (cita). Following good-of-fit testing, the model can be used to obtain the confidence intervals (CI) associated to the mean of SI and GI. Approaches, such as Monte Carlo and Markov-Chain Monte Carlo with a desired number of simulations can be used to approximate a distribution and obtain the parameters of the proposed model. Last, a time-to-event approach can be an alternative to determine the time until a given asymptomatic tree starts showing symptoms in a flush during a predetermined period.
Discussion
Plant disease epidemiology has borrowed many useful terms, principles, and methodologies from human disease epidemiology. In this review the concepts serial interval (SI) and generation interval (GI), which have been instrumental in the characterization of the transmission (symptomatic and asymptomatic) dynamics of a human disease of global concern: the COVID-19, are discussed. To our knowledge, the concepts SI and GI have not been used, at least explicitly, in plant disease epidemiology.
Upon an understanding of what these concepts entail, the questions that stand are: i) Are these epidemiological measures useful to the understanding of plant disease epidemics -specifically, of diseases caused by viruses and phloem-limited pathogens, such as CTV and CLas? and, If a “yes-answer” to this question holds, then ii) what would be some feasible and reliable approaches to field observation, experimentation and estimation of the distribution of those parameters? Like SARS-CoV-2, CTV and CLas exhibit a pre-symptomatic transmission period during which trees can be already contagious (Gottwald et al., 1999; Manjunath et al., 2008; Canale et al., 2020). The SI and from it the GI, can help elucidate this process, as it is based on symptom onset (which are easily observable) rather than on infection times (which are generally unknown). Both CTV and CLas have a long incubation period that can take even years to be completed. Furthermore, the distribution of the pathogen in a tree is not perfectly systemic at the onset of infection, and the incubation period may vary with the age of the plants and region. All of these characteristics make the early detection of infected individuals in an orchard even more difficult. In reducing transmission and spread of these diseases, then, early detection of infected individuals is essential for implementation of mitigation measures such as control of vector populations or eradication of infected tress. Reliable detection must be carried out by serological techniques such as ELISA (CTV) or molecular techniques such as RT-PCR (CLas and CTV). Recently, use of dog olfactory detection was proven to be a rapid, reliable and cheaper detection tool than molecular methods. For example, detection of infected asymptomatic individuals using efficiently trained dogs was demonstrated for both COVID-19 (Grandjean et al., 2020, 2021; Jendrny et al., 2020) and HLB (Gottwald et al., 2020) as an efficient alternative to this problem. Early detection methods could help estimate the SI and GI. In estimation of the SI and GI intervals for CTV and CLas, several considerations and major assumptions should be made regarding the host crop, vector, environment, as well as management practices that could affect pathogen transmission.
It follows that both the SI and GI could be useful to advance understanding of epidemics of these diseases. Our review suggests that usage and application of these parameters offer both challenges and research opportunities in the epidemiology of CTV and CLas. The major challenge is the elucidation of the role of the vector in pathogen transmission and spread as it relates to the duration of the infection time, incubation period, SI and GI. On the other hand, it is extremely difficult to determine when a citrus tree gets infected. Determining infectivity and transmission would require experiments on artificial releases of insects, caging of trees, or tree protection through insecticide applications, as done for other vectored-diseases. This could be coupled with detection of infected vectors and trees using serological, molecular or even animal olfactory methods. In contrast to COVID-19 epidemics in which mobility of the host affects transmission, in CTV and CLas epidemics, the main host exhibits no dispersal or mobility. Therefore, there is less uncertainty and subjectivity in the assignation of infecting pairs than in the contact-tracing data used for SI estimation in humans. Another question is if it is of any epidemiological relevance to define the SI and GI in the vector itself.
Conclusions
This review has introduced to plant pathologists the serial and generation intervals: two key epidemiological measures that have been used in human epidemiology to characterize the transmission dynamics (especially the pre-symptomatic transmission or asymptomatic spread) of a human disease of global concern. Both the definition and approaches to estimate their distribution were presented, with emphasis in approaches for identification of infector-infectee tree pairs in a transmission chain within an orchard, and methodologies used to estimate means and CIs for COVID-19. Like in COVID-19, asymptomatic transmission of CTV and CLas has been a major problem to effective implementation of disease control measures, for example vector control and eradication. It is hoped that this review awakes interest in further examination of the SI and GI measures or pursuance of their use or adoption. These epidemiological parameters could help advance understanding of the epidemiology of diseases of quarantine importance in which detection must be followed by eradication of diseased individuals.











 texto en
texto en 


