Introduction
Among academics, the discounted cash flow (DCF) is the most used method for valuing capital assets, but it is also criticized because it does not include important elements such as the occurrence of contingent events, the present risk in cash flows and volatility (Trigeorgis, 1996). The real options approach (ROA) serves as a complementary methodology to the DCF method, allowing to include volatility as a fundamental parameter to quantify risk and to collect some elements associated with uncertainty (Keswani & Shackleton, 2006). Trigeorgis (1996), Mun (2006) and Brandão, Dyer and Hahn (2012) have argued the difficulty of its estimation but have also indicated the importance of doing so appropriately to be able to perform an adequate valuation. Additionally, to assume that the volatility parameter is constant and unconditional, such as the one used in the ROA method, is considered impractical to model the price returns of financial series, capital assets and commodities, given the presence of a series of empirical characteristics such as leptokurtosis, heavy tail distributions, clustering volatility, and conditional variance that changes randomly over time (Grajales Correa & Pérez Ramírez, 2007).
According to this, it is necessary to make a good estimate of the real option for the ROA method, value that depends largely on the way that volatility is described and estimated. In other words, the option is very sensitive to the value that is calibrated for this factor, as demonstrated by Trigeorgis (1990), who in an analytical and empirical way concluded that an increase in that volatility by 50% could result in an increase by 40% of the real option. Concurrently, Keswani and Shackleton (2006) presented variations of more than 210% in the value of the real option when the volatility increases from 10% to 30% (Brandão et al., 2012). Taking the above into account, it was possible to conclude that the theory used to estimate the parameter of volatility contained in the ROA method has only been focused towards the calculation of its structure and its unconditional and constant behavior, without exploring the advantages that its conditional and stochastic estimation has (Vasseur, Sanchez, & Escobar, 2019).
In the last three decades, several studies have focused on volatility estimation, given its importance to economic agents and its use in financial and economic applications and because volatility plays an important role in decisions that involve financial risk (Posedel, 2005). It is common to find financial time series that exhibit some stylized facts, effects only began to be collected after the appearance of the most used classical models corresponding to the non-linear time series of autoregressive conditional heteroskedasticity (ARCH). This model was developed in the 1980s in the seminal works of Bollerslev (1986) and Engle (1982), who focused their efforts on including a functional relation between current and past conditional volatility as well as on describing the statistical distribution of the errors in detail (Argáez Sosa, Batún Cutz, Guerrero Lara, Kantún Chim, Medina Peralta, & Pantí Trejo, 2014). The previously mentioned models included the inertial behavior of volatility as well as the autocorrelation effect in all financial time series (Novales, 1993); that is, fundamentally, it is necessary to consider all the past information of a variable in predicting its current and future behavior (De Arce, 1998).
The ARCH generalization process to estimate conditional volatility was presented by Bollerslev (1986). His model of generalized autoregressive conditionally heteroskedasticity (GARCH) allowed multiple developments and extensions (Hansen & Lunde, 2005). The basis and simplicity of the functional structure of GARCH, specifically the type (1,1), has been considered to be the starting point for several financial applications (Preminger & Storti, 2017).
Recently, some models include stochastic volatility and were created, fundamentally, to overcome the underlying problems when considering volatility in terms of the evaluation time horizon. Motivated by this empirical evidence, several authors, such as Chesney and Scott (1989), Heston (1993), Hull and White (1987), Scott (1987), Stein and Stein (1991), and Wiggins (1987), proposed models with stochastic volatility as a parsimonious extension of the Black-Scholes model (Black & Scholes, 1973); among these models, the GARCH-diffusion type proposed by Drost and Werker (1996) and Duan (1996, 1997) excels. The novelty of this model is that it was the first approximation between a GARCH process and a stochastic volatility model. Additionally, multiple research developments of this model exist, both theoretical (Barone-Adesi, Rasmussen, & Ravanelli, 2005; Chourdakis & Dotsis, 2011; Christoffersen, Jacobs, & Mimouni, 2010; Ritchken & Trevor, 1999) and empirical (Figà-Talamanca, 2009; Plienpanich, Sattayatham, & Thao, 2009; Wu, Ma, & Wang, 2012; Wu, Yang, Ma, & Zhao, 2014).
This article is organized as follows. Section 2 describes the GARCH (1,1) type and the GARCH-diffusion model. Then, in section 3, the equivalence between the variance of these models is formally presented. Section 4 summarizes the multiplicative quadrinomial method to assess options, both real and financial. In section 5, some concepts to assess real options are summarized. Section 6 describes a counterfactual case as an example. Finally, section 7 includes discussion, conclusions, and suggestions for future research.
Volatility models
GARCH model
Volatility is a characteristic of any financial time series and, although it is considered non-constant, it is usually defined as homoscedastic and long-term estimates to be made. As it is unobservable, it is important to analyze and collect the oscillation that occurs in short-term, this is known as conditional volatility of the underlying asset (Casas Monsegny & Cepeda Cuervo, 2008). Based on this fact, Bollerslev (1986) and Engle (1982) developed models to analyze short-term conditional variations. Specifically, Bollerslev (1986) proposed the GARCH (p, q) model from the ARCH (q) model to overcome the weakness of estimating, in certain cases, many parameters, which complicate its estimation. Avoiding a possible loss of precision, a restricted alternative parameterization was defined, dependent on a reduced number of parameters. This model has the following structural form (Tsay, 2005):
where
with
This model can be used to emulate the conditional volatility, both the prices and the returns of financial assets as well as the risk value in portfolios and the exchange rates between currencies. For example, Casas Monsegny and Cepeda Cuervo (2008) used Gillette’s prices and found that this model explains their behavior to a large degree. Gazda and Výrost (2003) used data from the Slovakia Stock Index (SAX) to estimate the respective returns, using three different models - GARCH, exponential GARCH (EGARCH), and threshold GARCH (TARCH) - and found that the adjustment of the conditional variance could be achieved with any of these methods. Engle and Patton (2007) also used it in an index, specifically the Dow Jones, and reached the conclusion that the GARCH-type models help to capture different stylized facts offered by the market. Additionally, Martens (2002) modeled and forecast the volatility of the S&P500 futures index, using high-frequency data. Engle (2001) used the model to estimate the risk value in a hypothetical portfolio composed by 50% of the Nasdaq index, 30% of the Dow Jones index, and long-term bonds. Its use was also extended to other contexts, for example, exchange rates. Alexander and Lazar (2006) used it to model the American dollar in regard to three important currencies: Pound Sterling, Euro, and Yen; their main finding indicated that the empirical evidence favors the use of the normal mixture in conjunction with a GARCH (1,1) model. Hansen and Lunde (2005) presented an important work, in which it was indicated that the model was not surpassed by 330 similar and more sophisticated ARCH-like models. They arrived at this conclusion by using data on the exchange rate between the German mark and the American dollar; however, they also indicated that, when using the returns of IBM’s stock, the GARCH model apparently is not the most appropriate when a leverage effect is present.
GARCH-diffusion model
This model was introduced by Wong in 1964, but its popularity grew following the works of Nelson (1990a, 1990b). Drost and Werker (1996) and Duan (1996, 1997) were the first authors to propose an approximation between a GARCH process and the stochastic volatility model and to indicate that it is possible to exchange such processes as required, offering an important development for future research in such regard. Later, Ritchken and Trevor (1999) developed the same idea but expressed it in an algorithm to assess options, both European and American, based on the trinomial tree model. Subsequently, Barone-Adesi et al. (2005) analytically derived the first four moments of the model and obtained a closed solution to value an option; in addition, they analyzed the implicit volatility surfaces with this solution. An important condition was discovered by Christoffersen et al. (2010), who demonstrated empirically, through the use of realized volatilities, S&P500 returns, and an option data panel, that the Heston (1993) model was poorly specified, because in the diffusion model presented by the author, volatility was found in the square root instead of being considered linear. These conclusions were reaffirmed by Chourdakis and Dotsis (2011); although they also suggested that the model should consider a nonlinear drift against a linear one. Recent studies have indicated that this model gives a better description of the behavior and dynamics of financial series than other types of models, such as the well-known model of Heston (1993) (Aït-Sahalia & Kimmel, 2007; Jones, 2003; Wu, Zhou, & Wang, 2018). It has been used as a good model for adjusting financial option data (Chourdakis & Dotsis, 2011; Christoffersen et al., 2010; Kaeck & Alexander, 2012; Wu et al., 2012).
The most recent research on this model is considered to be empirical, and it has been used successfully in applications to different contexts; for example, Figà-Talamanca (2009) used multiple stock market indexes to compare the theoretical and empirical autocovariances, concluding that this model captures autocovariance observed in the data. At the same time, Plienpanich et al. (2009) integrated a disturbance through fractional noise into the diffusion model; their results showed that a better estimation of the stock price of a commercial bank was attained using this model rather than the traditional Black-Scholes model. Similar conclusions were obtained by Wu et al. (2012), who analyzed the Hang Seng index (HSI) and concluded that the GARCH-diffusion model offers better predictions of the price of warrants than the classical model. Years later, Wu et al. (2014) studied the Hong Kong stock market through American options and found the same advantage. Finally, Wu and Zhou (2016) used the Chinese volatility index (iVIX); their main findings indicated that the risk of volatility market values and the risk premium volatility were negative, which implied that investors in the Shanghai stock exchange are risk averse.
In general terms, this type of model is usually characterized by not having a closed solution and belongs to the class of non-affine models; in addition, solutions must be achieved through numerical methods, simulation, or the use of integrals in stochastic differential equations (Barone-Adesi et al., 2005). The system equations presented by this model have the following functional structure (Wu et al., 2012):
where the parameters α, θ, and σ are constant and equivalent to the mean-reversion speed, the mean long-term volatility or tendency, and the volatility of volatility, respectively. For its part,
Equivalence between conditional variance process of GARCH (1,1) and variance of GARCH-diffusion stochastic volatility model
Proposition 1. The functional structure GARCH (1,1) type presented in section 2.1, Equation (1.2) is equivalent to the differential equation proposed in (1.4), i.e. Vt is equivalent to
Proof.
As
It is easy to see that
Consider the variable
where,
From Equation (1.2) then,
Thus, the limit process of (1.6) is given by the stochastic differential equation
Figure 1 below shows a numerical experiment, graphically demonstrating the equivalence between the variance of these two processes.
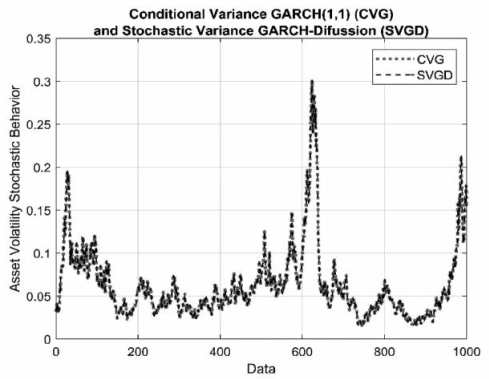
Source: Prepared by the authors with simulated data using MATLAB
Figure 1 Equivalence between the conditional variance of the GARCH (1,1) process with estimated parameters
As shown in Figure 1, the dynamics of the conditional and stochastic volatility generated for each are apparently the same, equivalent values being found among these processes.
Multiplicative quadrinomial tree model from the GARCH-diffusion model
Once the parameters have been estimated by the GARCH (1,1) model and its equivalents defined by the GARCH-diffusion model, the numerical method is derived using the multiplicative quadrinomial tree to describe the discrete behavior of the price of the underlying asset. The dynamic factors and transition probabilities are presented below.
Considering the proposed differential equation system given by (1.3) and (1.4), over the time interval [ ti, tk] , where µϵ , α ≥ 0, θ > 0 and σ > 0 are constant, while
To consider the recombination of two binomial trees
After all the corresponding parameters have been defined for Vt and for St, it is possible to construct a quadrinomial tree that emulates the behavior of price St, which, in each discrete step, has a value of branches equal to 4n, where n corresponds to the number of steps, but, when the respective recombination is performed, the number of branches decreases to n2, as can be seen in Figure 2b. Below we show the value of each position for the first step of the tree, as shown in Figure 2a (Pareja-Vasseur & Marin-Sánchez, 2019).
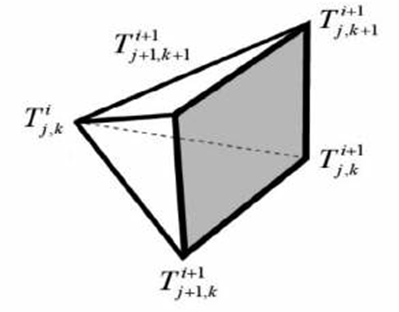
Source: Prepared by the authors using Photoshop
Figure 2a The first step of the proposed multiplicative quadrinomial tree model of the stochastic asset price and volatility.
Real option valuation
One of the techniques used to value the recent development of capital assets is known as ROA. This method, which is complementary to the DCF, seeks to introduce the volatility present in cash flows as well as the occurrence of contingent events. This methodology emerged from the theory of financial options but is applied when the valuation is performed for capital assets in real markets. This theoretical definition was coined by Stewart Myers, who indicated that many corporate assets could be seen as call options (Myers, 1977). This type of options, such as financial options, can be assessed using different techniques, of which the most appropriate corresponds to the numerical method with multiplicative binomial tree (Cox, Ross, & Rubinstein, 1979), because of its intuitive and simple handling. In this technique, the price in continuous time of an underlying asset approximates the Geometric Brownian Motion emulated through discrete time in the form of a tree, in which it is possible to analyze, graphically and numerically, the anticipated execution or otherwise of the option.
The ROA technique estimates the strategic net present value (NPV) and this value is compared with the static NPV, which is estimated in the traditional way using the DCF method, finding the real option value (Maya Ochoa & Pareja Vasseur, 2014; Mun, 2002; Trigeorgis, 1996). According to this theory, it is common for use options to differ, contract, expand, or abandon, among others; for American call and put options modified or adapted to that context.
Algebraic expression
Assume that the life of an option (real or financial) over an asset that does not pay
dividends, with an initial price S0 and exercise price
K, is divided into N sub-intervals, each
with duration
with T0=
In the case of an option to wait, the evaluation is performed in a similar way to an American financial call option; that is, the value on its maturity date is given by max (Tt - K): thus,
for j = 1,2,…,I and k=1,2,…,I, while its discounted value is defined as,
In the case of an expansion option, in which the expansion factor is defined by EF and K represents the additional investment for expansion, it is considered as a modified American call option, the value of which on its maturity date is given by max (T1 * EF-K,T1); therefore,
In the case of a contraction option, in which the contraction factor is defined by CF and, in this case, K represents the disinvestment or release of funds by contraction, it is considered as a modified American put option, the value of which on its maturity date is given by max(Tt, Tt * CF + K); hence,
for j = 1,2,…,i and k = 1,2,…,i . In addition, its discounted value is defined as,
In the case of an abandonment option, in which the salvage value corresponds to K in this case, it is considered as a modified American put option, the value of which on its maturity date is given by max (T t , K) ; thus,
for 1,2,…,i and k = 1,2,…,i. In addition, its discounted value is defined as follows,
Application example
Methodology
The methodology used in this paper is based on deductive logic and it is classified as quantitative, descriptive and non-experimental, besides as longitudinal respect time series (Hernández, Fernández, & Baptista, 2010). The methodology here presented rest on the use of a deductive logic and it is possible to classified as theorical, quantitative, non-experimental and longitudinal through time series analysis. It is formalized via econometric, mathematic and computational tools. We built a quadrinomial recombination in a non-constant volatility environment, that implied for its construction a rigorous mathematic deduction, which one was applied to value the real option of an oil sector project. Accordingly, the whole investigation could be considerate as an illustrative case, based on Hayes, Kyer and Weber (2015) from a quantitative point of view.
Data collection
The data series was extracted from the Bloomberg platform and its WTI (West Texas Intermediate) oil futures quoted prices with ticket CL1, with an operating contract for 1 000 barrels. The commodity has been listed on Bloomberg since March 30, 1983, but the sample used was obtained from January 1, 2013 to August 14, 2018, resulting in a total of 1 466 observations. Due to the liquidity of this type of contract, it is common to use it as a point of reference for the most of crude international prices. Figure 3 shows the commodity prices.
Data analysis
Table 1 presents some of the most relevant news that affected the commodity price in the market, which suggested important variations in the behavior of this variable.
Table 1 Main events that influenced the WTI oil price variation in the sample
| Date | Event | Price (USD) |
| April 18, 2013 | The price was the lowest for that year, due to low gasoline production and low oil demand | 86.68 |
| September 5, 2013 | The price was the maximum for that year, because President Barack Obama spoke about possible military intervention in Syria | 108.37 |
| January 9, 2014 | The price fell and broke the USD 100 barrier, due to a rebound effect that resulted from high speculation | 91.66 |
| March 17, 2015 | The market showed a downward trend since 2014, and the price reached the USD 40 level. The explanation was related to the weakness of the dollar value 43.46 and the expectation of the policy report of the Federal Reserve | |
| August 24, 2015 | After a brief rise in the oil price since April of that year, it collapsed because | 38.24 |
| February 11, 2016 | This was the lowest price for the entire data series, mainly due to oversupply in the market and the level of the barrel inventory in Cushing, Oklahoma (the largest stockpile place in the US) | 26.21 |
| June 8, 2016 | The price increased due to political conflicts in Nigeria that affected supply and reduced oil reserves in the US | 51.23 |
| August 2, 2016 | The price fell below USD 40 again, due to excessive supply of crude oil and low dollar price | 39.51 |
| June 21, 2017 | This was the lowest price in 2017; again, a direct effect of oversupply, due to high levels of stockpiles in the US, and from this moment, the price showed relative growth until the date on which the data were extracted | 42.53 |
Source: Prepared by the authors with information taken and adapted from the Bloomberg platform (2018).
Results
Price series results
Figures 4a and 4b (see Appendix) offer the descriptive statistics and a correlogram (Box, Jenkins, Reinsel, & Ljung, 2015) for the selected commodity price series; as it can be seen, there seems to be the first-lag autocorrelation, meaning that the price on one day is correlated with that on the next. As a complement, Table 2 presents the finding formalized with the Breush-Godfrey test (Breusch, 1978; Godfrey, 1978), In this case, we detect autocorrelation of order 1 in the price residuals.
Table 2 Breusch-Godfrey serial correlation LM test
| Variable | Coefficient | Std error | t-statistic | Prob. |
| C | -7.76And-05 | 0.034304 | -0.002262 | 0.9982 |
| RESID(-1) | 0.963292 | 0.026130 | 36.86560 | 0.0000 |
| RESID(-2) | 0.035201 | 0.026130 | 1.347177 | 0.1781 |
Note: Two lags are included
Source: Prepared by the authors using EViews.
The result shows that the alternative hypothesis is not rejected and that there is a serial
correlation of some order, in this case, for the first lag. Based on this, we
can define, analyze, and model the variable using a system of stochastic
differential equations of the GARCH-diffusion type. Once the equation for the
price has been defined, the yields are estimated as an alternative to detect
conditional volatility, as stated in the following Equation, which is derived
from (1.3):
Thus,
Yield series results
In this section, we present the analysis of the WTI oil yield series estimated from Equation (1.9). We present the descriptive statistics (Figure 5a), and graphically check stationarity (Figure 5b), autocorrelation (Figure 6a), and heteroskedasticity (Figure 6b); suggesting conditional volatility, it should be estimated through ARCH models. As a complement, some tests are presented below, to verify the previous characteristics. The following statistical tests were performed: the Kwiatkowski-Phillips-Schmidt-Shin test (Kwiatkowski, Phillips, Schmidt, & Shin, 1992), to detect if the series was stationary on average; the Breush-Godfrey test, to detect presence of serial autocorrelation; and the Ljung-Box Q test (Ljung & Box, 1978) and Engle ARCH test (Engle, 1982), to check for heteroskedasticity in the series. The results are as follows:
The results were evaluated with an Alpha value of 10%. Thus, the series is apparently stationary on average, since the null hypothesis should not be rejected for any of the critical values (Table 3); the series also apparently has autocorrelation of order 1, because the one residual lag is significant (Table 4); and, finally, there is heteroskedasticity as indicated by the two tests (Ljung-Box and Engle ARCH). We have satisfactory evidence to reject the null hypothesis that the series does not have significant ARCH effects (Tables 5 and 6).
Table 3 Kwiatkowski-Phillips-Schmidt-Shin test
| LM stat. | ||
| Kwiatkowski-Phillips-Schmidt-Shin test statistic | 0.088610 | |
| Asymptotic critical values: | 1% level | 0.216000 |
| 5% level | 0.463000 | |
| 10% level | 0.347000 |
Note: The trend and intercept are included.
Source: Prepared by the authors using EViews
Table 4 Breusch-Godfrey serial correlation LM test
| Variable | Coefficient | Std error | t-statistic | Prob. |
| C | 6.69And-06 | 0.008658 | 0.000773 | 0.9994 |
| RESID(-1) | -0.067052 | 0.026155 | -2.563647 | 0.0105 |
| RESID(-2) | -0.003275 | 0.026156 | -0.125199 | 0.9004 |
Note: Two lags are included.
Source: Prepared by the authors using EViews
Table 5 Ljung-Box test
| Stat. | p-value | c-value |
| 127.8451 | 0 | 3.8415 |
Note: One lag is included.
Source: Prepared by the authors using MATLAB.
Findings
Parameter estimation corresponding to the GARCH (1,1) process
Once the statistical tests had been applied to the yield series, we move on to estimate the value of each of the parameters using a GARCH (1,1) model as presented in Equation (1.2) to find their equivalents in the GARCH-diffusion model, as presented later.
Table 7 GARCH (1,1) estimation process for the WTI oil yield series
| Variable Variance Equation |
Coefficient | Std error | z-statistic | Prob. |
| C | 0.000496 | 0.000224 | 2.219792 | 0.0264 |
| RESID(-1)^2 | 0.061478 | 0.008451 | 7.274757 | 0.0000 |
| GARCH(-1) | 0.935966 | 0.008894 | 105.2315 | 0.0000 |
Note: With unconditional prevariance.
Source: Prepared by the authors using EViews.
Table 7 shows the results and indicates that the coefficients are significant with an Alpha value of 10%; thus, the estimation has the following structural form:
Figure 7a exhibits the WTI oil yield conditional volatility for the established dates; in addition, the yield residual squared correlogram was estimated to verify that there was white noise (Figure 7b).
It can be seen in Figure 7a, that there are three volatility clusters defined: The first has low volatility from 2013 to mid-2014, the second has high volatility until the end of 2016, and the third shows some lower volatility until the end. On the right side, Figure 7b presents the residuals squared correlogram, in which the series contains white noise, which is completely random. To conclude this section, the estimation of the WTI oil price versus the real prices for the given range is presented below. The forecast was constructed from the information offered by the GARCH (1,1) conditional volatility process and then a random number series was generated to estimate the respective residuals, as shown in Equations (1.8) and (1.9), the forecast is presented in Figure 8.

Source: Prepared by the authors using Matlab.
Figure 8 WTI oil real prices versus estimated prices using the conditional volatility of GARCH (1,1) model.
As it can be observed in Figure 8, the estimated
prices and the real ones were close to each other, and to verify this
result, the mean square error was used. The result of 1.61 indicates that
the estimation was robust and followed the dynamics of the process. The
estimated prices were built using Equations (1.8) and (1.9), as follows:
Equivalence between the values of the parameters of the GARCH (1,1) model and those of the GARCH-diffusion model
From the equivalence between the variance of processes detailed in section 3, Table 8 offers the values of the
parameters between the GARCH (1,1) model and the GARCH-diffusion model using
Equations:
Real option valuation: a counterfactual case
As a counterfactual case, in this section we discuss a real option valuation using the algebraic expression of an option of abandonment, as described in section 5.1. To find the value of the strategic NPV, the numerical method was employed by means of quadrinomial trees with the stochastic volatility model presented in section 4 and considering the values estimated for the GARCH-diffusion model exhibited in Table 8, which are the parameters of Equation (1.4). Finally, the solution was compared with the estimated results of the traditional multiplicative binomial method.
Suppose the oil company “X” based its efforts exclusively to upstream process. This firm signed an exploration and production contract (E&P), where a determinate area was assigned to them, which one is used to exploration, evaluation and oil extraction. The development of contract E&P counts with a geological and geophysical analysis and wanted to know the strategic NPV value of a project according to the ROA methodology and that its cash flows can be modeled using Equations (1.3) and (1.4). Assume the WTI oil prices used to estimate the cash flows are perfectly correlated with the project and volatility is the same that project without administrative flexibility has (Brandão, Dyer, & Hahn, 2012). The estimated static NPV of the project is affected by the technical probability and corresponds to S0=T0=91.82, which was calculated according to the traditional DCF methodology with an appropriate risk-adjusted rate. Besides that, is estimated the technical probability or the geological success depends on the occurrence probability of these factors, as basement, caprock, reservoir rock, and its own dynamics. The previous information allowed to find the technical probability as the probability product sequence mentioned before.
The firm also determined that it has an opportunity to assign the rights and property of the project to a third party at the value of K = 66 when the market conditions are unfavorable. That is, this value corresponds to the salvage value and remains constant over the evaluation horizon of the firm’s abandonment option (Pareja Vasseur & Cadavid Pérez, 2016). Assume, in addition, the following values that were obtained from the GARCH (1,1) estimation process of the WTI oil price yields between January 2013 and August 2018 and their equivalents for the GARCH-diffusion model (see Table 8):
The results of the strategic NPV for the periods from year one to year five, with annual
steps, are summarized in Table 9. It can be
seen in all the cases that value estimated by our proposed method is higher than the
traditional one. This would indicate an undervaluation of the strategic NPV at
estimating lower volatility than the one actually presented in the series.
Specifically, the first row shows the values for our methodology; for example, for
the fourth year, a strategic NPV is estimated at 104.57, with an abandonment option
of 12.75, whereas using the traditional method with multiplicative binomial trees,
that is, the second row, the results are 99.99 and 8.17, respectively. The last row
of Table 9 shows the percentage differences
between the NPV values of the two methods, concluding that there is an approximate
average of 5% for all the years of the real option evaluation. It is important to
state that, if constant volatility 44.06% had been used in the traditional
methodology, which comes from
Table 9 Comparison of the value of the strategic NPV through the quadrinomial method and the binomial method
| Method/time | 1 | 2 | 3 | 4 | 5 | |
| (1) | Quadrinomial tree | 95.59 | 100.09 | 102.37 | 104.57 | 106.31 |
| (2) | Binomial tree | 91.88 | 96.93 | 96.96 | 99.99 | 100.01 |
| (3) | Difference in percentage | 4.04% | 3.26% | 5.58% | 4.58% | 6.30% |
Source: Prepared by the authors using MATLAB and Excel.
Conclusions
The findings can be summarized as follows. First, the price analysis helps to detect first-lag autocorrelation, which suggested that there was evidence of conditional heteroskedasticity in the time series chosen as the sample. Second, with the price we detected three different volatility clusters for the WTI oil, two with moderate volatilities, the first between 2013 and 2014 and the second between 2017 and 2018, and one with high volatility for 2015 and 2016. This implies that volatility is not constant but dynamic and for that reason, it should be modeled in the latter form. Third, once price yields were estimated, it was possible to use a statistical test at the 10% significance Alpha level to look for stationarity, autocorrelation, and heteroskedasticity, suggesting that the price variations of WTI oil have conditional volatility depending on the time. Fourth, it was possible to estimate a GARCH process for the WTI oil commodity and model its variance using a GARCH (1,1) model. We found out that the residuals after the estimation were white noise, that is, completely random. Fifth, using mathematical and statistical development, it was possible to find an equivalence between the GARCH (1,1) conditional volatility and the stochastic variance of the GARCH-diffusion model. The latter provided elements to build and develop the numerical method by trees to assess options that are derived from the behavior of this commodity type. Sixth, it was possible to use an algebraic expression to depict the evolution of the price of an asset in presence of both dynamic and constant volatility in such a way that its effect is captured in an appropriate manner, to model the evolution or behavior of the underlying asset in the market. Seventh, it was concluded that the real option value is higher in our method than the binomial method, because “real” volatility is greater than that estimated by traditional simple standard yields deviation. It was also indicated that, when the traditional binomial method uses
Future research aims to analyze how it changes the quadrinomial method when there is a correlation between Brownian Motions. At the same time, using different commodities as real options applications with the proposed methodology is also necessary. The appropriate analysis is advocated to determine the initial volatility value for proposed method, since changes in this variable produces significant variations in real option assess.
Finally, this research connects the areas of econometrics and stochastic processes, verifying that there is existence of a relationship between variances of the GARCH (1,1) model and the GARCH-diffusion model; therefore, in this line of research, future research could demonstrate the equivalences that could exist between the different models of the ARCH family and their equivalents in the stochastic differential equations system to obtain better estimates of derivatives’ prices and accordingly to facilitate a deeper, developed, and efficient market.











 nueva página del texto (beta)
nueva página del texto (beta)










