1. Introduction
The importance of oil in the world economy will continue during this century as a unique raw material -responsible both for power generation and for producing a number of derivatives- and will continue to have a huge influence on the industrial sector. The behavior of the price of this raw material has received much attention over the years due to its effect on energy costs, global economic growth and public finances, and growth for both net oil exporters and net importers. Therefore, oil reserves and prices are present in all economic and financial discussions. Not only are equity markets particularly sensitive, so are other commodity markets, as well as financial products related to oil prices.
In this article, we focus on Mexico, a country that was until recently a net exporter of hydrocarbons, and which is now rapidly becoming a net importer of these. Because of the impact of such changes on government finances, economic activities, exchange rates and, consequently, the stock market, the study of the relationship between them is relevant.
Duran, Lorenzo and Armenta (2011), who examined the effect of oil-price volatility on Latin American stock market returns, found that stock market returns depend mainly on oil market returns. In our study, we take this analysis one step further, estimating the conditional probability that an increase (decrease) in Mexican oil prices will increase (decrease) Mexican stock market returns (represented in this study as a change in the IPC, the Index of Prices and Quotations, the main indicator of the Mexican Stock Exchange).
In particular, we estimated the conditional dependence of the IPC on oil prices. We use the reference of the price of the MAYA crude oil blend, because, by volume; MAYA is Mexico’s’ main export crude grade (for this study we identify this reference as MECOB). Mexico is an oil producing country, and changes in oil prices are directly transmitted into its economy through its markets and BRENT oil price reference. We decided to use the BRENT oil price reference because approximately two-thirds of all crude contracts around the world reference Brent Blend, making it the most widely used benchmark.
In order to appropriately describe the behavior of an asset, in this case the IPC, it is necessary to measure the volatility of its returns. Several analyses have tested the relation between oil returns and financial markets in terms of their volatilities. Macroeconomic factors, volatility and conditional dependence have been used to explain this relationship.
In particular, GARCH approaches have been used to model and describe the volatility of these assets with good results in the literature. For example, Hamilton (1983) used a GARCH model to find evidence that an increase in oil prices explained the decrease in expected earnings of the stock market that he analyzed. He also found that when the financial market is not efficient, the adjustment of the stock market in response to oil price changes may not be immediate. Jones and Gautam (1996) looked at oil price volatility as one explanatory variable for financial market returns. Huang, Masulis and Stoll (1996), whose article is a benchmark in literature for these kinds of studies, considered the impact of oil price volatility under a GARCH approach, using a VAR model. Lorenzo, Duran and Armenta (2012) estimated a BEKK model and generated conditional correlation series between Mexican financial market volatility and oil price volatility.
This study uses the conditional dependence approach of Lorenzo, Duran and Armenta (2012), which hypothesized conditional dependence of financial market returns on oil prices and applied this hypothesis to Mexican data under a BEKK model. In the present study we use a copula model approach for marginal distribution of returns in order to describe the tail dependence between oil prices and the Mexican stock market index. The structure of this work is divided as follows: The next section contains a literature review, emphasizing Mexican references on this topic. The third section explains the methodology, beginning with the copula concepts and GARH models. In the fourth section we present empirical results, and conclude in the fifth section.
2. Literature review
The effect of macroeconomic variables on the stock market, and in particular the relationship between oil price shocks and stock prices, has been extensively analyzed; for example, in Chen, Roll and Ross (1986). Even by looking for an impact of oil prices on economic growth, on the macroeconomy as a whole or at the relationship between oil prices and certain macroeconomic variables, or specific industries, researchers keep studying this topic, such as in Hamilton (1983); Mork (1989); Lee, Ni and Ratti (1995); Hooker (1996) and Barsky and Kilian (2004). Many studies have shown that economic activity is inversely related to oil price changes, including Hamilton (1983); Burbidge and Harrison (1984); Gisser and Goodwin (1986); Loungani (1986); Mork (1989); Lee, Ni and Ratti (1995); Mork, Olsen and Mysen (1994); IMF (2000); Jones, Leiby and Paik (2004). These results are evidence of the relationship between the oil and the stock markets. Although the relationship varies among different countries or regions, these studies are all relevant to this study since they show a significant relationship between these two variables.
The analysis of the relationship between oil prices and stock markets in developed countries has been a specific focus of a number of studies. Jones and Kaul (1996) performed their analysis for the US, Canada, Japan, and the UK, concluding that increases in post-war oil prices are negatively correlated with stock prices. These researchers, together with Papapetrou (2001), reached the conclusion that the US and Canadian markets reacted as expected by directly absorbing the oil price shocks into their current and expected future real cash flows (a conclusion that the previous studies don’t mention). Huang, Masulis and Stoll (1996) studied the dynamic interactions between oil future prices and the US stock prices. They examined the effects of energy shocks on financial markets, and found a significant nonlinear relationship between actual stock returns and crude oil futures’ prices. Sadorsky (1999) confirmed the same negative correlation for the US Park and Ratti (2008) found an asymmetric, but negative, impact from oil prices on stock returns in many European countries. The negative correlation was also found by Miller and Ratti (2009) in their study of six OECD countries.
The analysis of the relationship between oil prices and stock markets has tended to confirm the relationship between these two variables using many different techniques, such as cointegration analysis, conditional correlation, impulse response functions, vector autoregression models (VAR), vector error correction models (VECM), multivariate threshold models and other time series techniques, as in Jones and Kaul (1996); Huang, Masulis and Stoll (1996); Sadorsky (1999); Papapetrou (2001); Huang, Hwang and Hsiao-Ping (2005); Jimenez-Rodriguez and Sanchez (2005); Cong et al (2008); Adam and Tweneboah (2008); Apergis and Miller (2009); Miller and Ratti (2009); Narayan and Narayan (2010); Filis (2010); and Arouri and Rault (2010). We observe that, according to Sadosky (1999), the stock market explained most of its own variance, although in the second period of his analysis (1986-1996) oil prices had an asymmetric effect on the stock market. He found that during this period, negative oil price shocks had a greater effect than positive ones.
There are few studies about the Mexican market. Hammoudeh and Li (2005) tested the effect of oil prices on the stock markets of Norway and Mexico, for the period of 1986-2003, using a VAR model that provided evidence that both stock markets indices were highly positively affected by rising oil prices. Imarhiagbe (2010) analyzed the impact of oil prices on stock prices in six countries (including Mexico), for the period of 2006-2010. He modeled a cointegrated system in VAR analysis. The results showed that it is not clear that long-run cointegration exists for Mexican oil price and stock market data. Lorenzo, Duran and Armenta (2012) analyzed the relationship between the oil price (using Brent reference prices) and the returns of companies listed on the Mexican Stock Market for 208 weeks from 2006 to 2010. The results showed a positive conditional correlation using a BEKK model.
The effects of Brent oil prices on stock markets were also analyzed by Duran, Lorenzo and Armenta (2011), using a TGARCH approach to show the asymmetric effects caused by oil returns on the volatility of the stock market in seven Latin American countries. For Mexico, they did not find that oil price volatility had an asymmetric effect on the volatility of stock prices.
In order to study the time-varying dependence structure between oil price changes and stock market returns, the literature has commonly used multivariate GARCH models. Unconditional and time varying copula GARCH models have been used by Reboredo (2011), who found that symmetric tail dependence was well captured by a Student-t copula for the WTI-Brent, WTI-Dubai, WTI-Maya and Dubai-Maya pairs. Nguyen and Bhatti (2012) for China and Vietnam; and Zhu, H., R. Li, and S. Li (2014) for ten Asia-Pacific economies studied the dependence structure between crude oil prices and stock returns. Nguyen and Bhatti (2012) showed left tail dependence for Vietnam but no tail dependence for China. Zhu, Li and Li (2014) provide evidence of a weak dependence between crude oil prices and the Asia-Pacific stock markets.
However, Wen, Wei and Huang (2012) provided evidence of symmetric tail dependence (i.e. tail dependence for both increases and decreases in oil prices) for US and Chinese stock markets, although the contagious effect was found to be much weaker for China than for the US. The use of three Archimedean copulas, applied by Aloui, Hammoudeh and Nguyen (2013) to six East European Countries and Naifar and Al Dohaiman (2013) to six Gulf Council Countries found dependence between oil prices and stock market prices under different methodologies (symmetric tail, asymmetric tail, copulas).
To examine the dependence between oil price and stock market, copulas analyses have been used in many studies. German and Kharoubi (2008) used WTI futures prices and the S&P 500 index.
Zohrabyan (2008) used BRENT crude oil spot FOB price and the OPEC oil basket price for stock markets from Japan, the UK, Germany, France, the Netherlands, Italy, the US, Spain, Finland, Canada, Switzerland, Poland, the Czech Republic, Hungary, China, Russia, Hong Kong, Venezuela, and Saudi Arabia. These studies show asymmetrical dependence between oil prices and stock market indices, with a negligible difference between the copula results for developed and developing countries. The present study provides evidence of the short run analysis of the conditional relationship between oil prices and the Mexican stock market from January 2010 to May 2014.
3. Methodology
Copula modeling allows multivariate distribution functions to be described by means of their marginal distribution functions and a dependence function named copula. The theoretical and practical aspects are presented by Nelsen (1999). The aim is to isolate the dependence structure from the structure of the marginal distributions.
A bivariate copula C(u 1,u 2) is a cumulative distribution function (CDF) with uniform marginal distribution functions on the unit interval. Sklar’s theorem (Sklar, 1959) states that if F j (x j ) is the CDF of two univariate continuous random variables X j , j = 1, 2 then C (F 1(x 1), F 2(x 2)) is a bivariate CDF for X = (X 1, X 2), with marginal distributions F j Conversely, if F is a continuous bivariate CDF with univariate marginals F 1,F 2, then there is a unique bivariate copula C such that F(x 1, x 2) = C (F 1 (x 1), F 2 (x 2)).
The properties of copulas allow us to study dependencies more easily in financial markets. Among these properties, we first mention that copulas are invariant to monotone transformations of random variables. Second, there is a direct relationship between the parameters of copulas and measures of concordance, as widely used by Kendall’s τ (tau). Third, they provide an asymptotic dependence treatment in the tails of the distributions.
Kendall’s τ (tau) is a measure of concordance between two random variables. Two points (x 1, x 2), (y 1, y 2) are said to be concordant if (x 1 − y 1)(x 2 − y 2) > 0, and discordant if (x 1 − y 1)( x 2 − y 2) < 0. Likewise, two random vectors (X 1, X 2), (Y 1, Y 2) are concordant if the probability P [(X 1, − Y 1)(X 2 − Y 2) > 0] is greater than P [(X 1, − Y 1)(X 2 − Y 2) < 0]; that is, X 1 and X 2 tend to increase together. They are discordant if the opposite happens. Kendall’s τ (tau) measures differences in probability.
Kendall’s τ (tau) is related to copulas through the following equation:
Another dependence measure defined by copulas is the asymptotic tail dependence, which measures the performance of random variables during extreme events. In this paper, we use a parameter to measure the probability that an extreme increase (decrease) in oil prices occurred, if we observe an extreme increase (decrease) in Mexican index returns.
The lower τ L and upper τ U asymptotic tail dependence coefficients are defined as:
There is independence in the tail if the value is zero, and dependence if the value is between zero and one. If the value is one, there is perfect dependence.
In this study, Clayton and Gumbel copulas are used. The Clayton copula shows lower tail dependence, while the Gumbel copula shows upper tail dependence.
The bivariate Clayton copula is given by:
 where θ ∈ [−1, ∞)\{0}. In this case τ
L
= 2
-1/θ
.
where θ ∈ [−1, ∞)\{0}. In this case τ
L
= 2
-1/θ
.
The bivariate Clayton copula is given by:
where θ ∈ [−1,∞). 0 For this case τ U =2−2 -1/θ .
For this study, the conditional tail dependence measures were estimated following Patton (2006). The lower τ L and upper τ U tail coefficients are supposed to be time dependent. The evolving dynamic is as follows:
where Λ is the logistic transformation used to keep the values between zero and one.
To describe the marginal behavior, we use the closing prices of the Mexican stock index and two different oil prices: MECOB crude oil prices (for the Mexican reference crude) and BRENT prices subscribed i at time t, P it Continuous returns are calculated as follows:
We also examined the volatility of the stock market returns and the oil returns using a TGARCH model. For the conditional mean, we used an AR(1) model, and to allow for a leverage effect, we considered a TGARCH model following Zakoian (1994) for the conditional variance equation. Thus, the complete model used in this work is:
This model takes into account that innovations ε it are distributed as a standardized t Student, and that the degrees of freedom (ν) are estimated. Innovations have differentiated impacts on the conditional variance. Positive innovations (u t-1 > 0) have an impact γ i . Negative innovations (u t-1 < 0) have an impact α i1 + γ i . Particularly, if γ i . > 0, a “leverage effect” will occur and negative news will increase volatility.
For the estimation of the parameters, the log likelihood function used is:
where c(F 1(r 1t ; α 1), F 2(r 2t ; α 2); θ) is the copula density; and f 1 and f 2 are the marginal densities of the IPC returns and oil price returns, respectively.
4. Empirical results
We collected weekly data for Mexican stock index (IPC), MECOB crude oil reference prices for Mexico, and BRENT oil prices for the period between January 1st, 2010 and May 30, 2014.
Weekly continuous returns of the three sets of data are presented as calculated using Equation (7). Descriptive statistics are presented in Table 1.
Table 1 Descriptive statistics of returns of Mexico stock index (IPC), MECOB and Brent oil prices.
| IPC | MECOB | IPC | |
| Mean | 0.00116 | 0.00127 | 0.00152 |
| Std. Dev. | 0.02154 | 0.03277 | 0.02695 |
| Skewness | -0.23003 | -0.38188 | 0.01853 |
| Kurtosis | 3.84872 | 4.37181 | 3.38932 |
| Jarque-Bera | 8.93148 | 23.62482 | 1.46573 |
| Probability | 0.01150 | 0.00001 | 0.48053 |
| Correlation | 0.36417 | 0.25117 | |
| Kendall’s τ (tau) | 0.17775 | 0.12033 |
Source: Elaborated by authors using data from ECONOMATICA (IPC and MECOB) and US Energy Information Administration (BRENT).
The non-normality of returns is confirmed for the IPC and MECOB, but not for BRENT, by the Jarque-Bera statistic based on kurtosis and skewness. The correlation coefficient is a measure of linear dependence. If this value is one, there is a perfect positive linear dependence, and if it is negative one, there is a perfect negative linear dependence. The 36% positive linear correlation between IPC and MECOB returns, and the 25% positive linear dependence between IPC and BRENT returns, confirms a level of linear dependence. The Kendall’s τ (tau), explained in section 3, confirms the dependence between the IPC and oil price returns.
Figure 1 shows time series plots in price levels and returns of IPC, MECOB and BRENT. It can be observed that in volatile periods there is a relationship between the returns of the stock index and oil returns. The results of the estimation of the Clayton copula (Equation 4) and the Gumbel copula (Equation 5) with their own marginal behavior of returns as in Equation (8) are presented in Table 2 and Table 3, respectively. The estimation of different parameters and their p-value for the full sample appear there also, as well as the estimator of the degrees of freedom of the t-Standard distribution.
Table 2 Clayton copula parameter estimators and y p-value for IPC with MECOB and IPC with BRENT returns respectively
| IPC | MECOB | IPC | BRENT | |||||||||
| Coef. | Prob. | Coef. | Prob. | Coef. | Prob. | Coef. | Prob. | |||||
| φ 0 | .00087 | .48358 | .00080 | .66775 | φ 0 | .00084 | .53333 | -.00103 | .44082 | |||
| φ 1 | -.05597 | .37309 | -.00138 | .98357 | φ 1 | -.08432 | .20420 | .27018 | .00000 | |||
| α 0 | .00003 | .06758 | .00001 | .00000 | α0 | .00004 | .18011 | .00003 | .00000 | |||
| α 1 | -.20475 | .01743 | -.05454 | .00000 | α 1 | -.25173 | .05035 | -.02077 | .05009 | |||
| γ | .46364 | .00708 | .06026 | .00000 | γ | .54928 | .04221 | .14011 | .05045 | |||
| β | .90413 | .00000 | 1.01646 | .00000 | β | .90938 | .00000 | .99914 | .00000 | |||
| ν | 6.1316 | .0689 | 5.3270 | .0043 | ν | 4.2420 | .0229 | 3.1582 | .0000 | |||
| λ 0L | -1.38846 | .53772 | λ 0L | -.63848 | .82889 | |||||||
| λ 1L | .47870 | .96154 | λ 1L | -.35178 | .96947 | |||||||
| λ 2L | -.45158 | .87023 | λ 2L | -.30057 | .86515 | |||||||
| Logl | 1058.77 | Logl | 1086.23 | |||||||||
| Akaike | -9.13834 | Akaike | -9.37925 | |||||||||
Source: Elaborated by the authors using programs designed EVIEWS.
Table 3 Gumbel copula parameter estimators and y p-value for IPC with MECOB and IPC with BRENT returns respectively
| IPC | MECOB | IPC | MECOB | |||||||||
| Coef. | Prob. | Coef. | Prob. | Coef. | Prob. | Coef. | Prob. | |||||
| φ 0 | .00161 | .18202 | .00146 | .48011 | φ 0 | .00139 | .24616 | -.00012 | .93144 | |||
| φ 1 | -.09801 | .12216 | -.02093 | .73052 | φ 1 | -.07786 | .23877 | .25446 | .00002 | |||
| α 0 | .00003 | . 09447 | .00000 | .02909 | α 0 | .00003 | .11594 | .00001 | .00000 | |||
| α 1 | -.21530 | .00000 | -.03524 | .00000 | α 1 | -.22196 | .02446 | -.03816 | .00000 | |||
| γ | .49536 | .00046 | .01542 | .00000 | γ | .48051 | .01753 | .07853 | .00000 | |||
| β | .89265 | .00000 | 1.01860 | .00000 | β | .91018 | .00000 | 1.01384 | .00000 | |||
| ν | 5.2226 | .0477 | 4.6510 | .0037 | ν | 5.2531 | .0525 | 4.6954 | .0005 | |||
| λ 0U | -1.88379 | .00000 | λ 0U | -1.91528 | .00282 | |||||||
| Λ 1U | 4.13794 | .00000 | Λ 1U | 4.29583 | .02303 | |||||||
| Λ 2U | -.94935 | .00000 | Λ 2U | -1.18183 | .38658 | |||||||
| Logl | 1051.56 | Logl | 1097.45 | |||||||||
| Akaike | -9.07509 | Akaike | -9.47765 | |||||||||
Source: Elaborated by the authors using programs designed EVIEWS.
We reviewed the correlograms of the residuals and squared residuals, applying the Q-statistic test to ensure that they behave like white noise. We found this to be the case. A leverage effect, measured by the γ parameter, is statistically confirmed for the stock index and for the oil returns in both models.
The parameters of the equation for lower tail dependence in the Clayton copula τ L, and upper tail dependence in the Gumbel copula τ U are also presented in Table 2 and Table 3 respectively, and were used to obtain the time series of dependence presented in Figure 2.
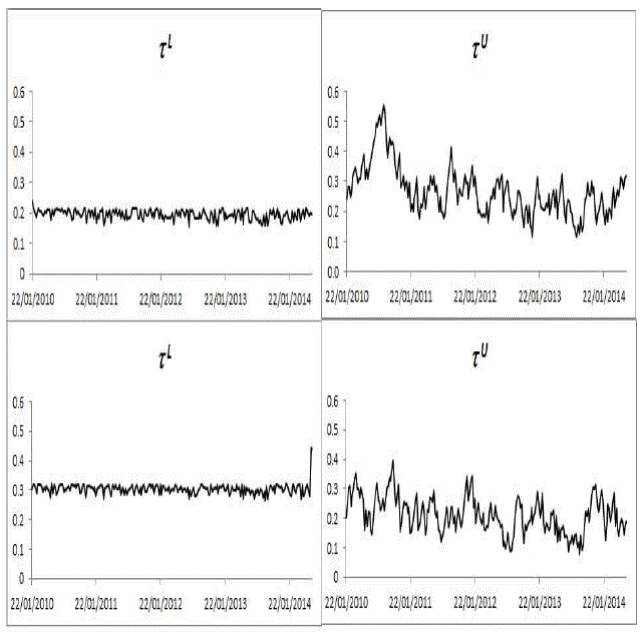
Figure 2 Lower (τ L ) (left) and upper (τ U ) (right) conditional tail dependence time series probabilities for IPC, with MECOB (above) and BRENT (below)
Figure 2 shows lower conditional tail dependence, indicating a probability that decreases in Mexican stock returns were caused by increases in oil returns. Since the parameters of the equation for lower tail dependence in the Clayton model are not statistically significant, this probability is approximately 0.5% (the logistic distribution evaluated in zero).
On the other hand, the Gumbel model shows a higher probability that the increases observed in the Mexican stock returns were caused by increases in oil returns. The effect is more volatile and present, and shows autoregressive behavior, since the parameters of the equation for upper tail dependence in Gumbel are statistically significant. This probability varies in the study period, ranging from 11.4% to 55.5%; in the case of MECOB, and from 7.5% to 39.5% for BRENT.
Thus, estimation of the Clayton and the Gumbel copulas indicates a low probability that an extreme decrease in IPC prices will result from an extreme decrease in the oil prices (0.5%), but a high probability that an extreme increase in IPC prices is time dependent on an extreme increase in the oil prices.
5. Concluding remarks
In this paper, we present empirical evidence of tail dependency between the Mexican stock market and the oil market for the period of study. We analyzed weekly closing prices for the Mexican stock index (IPC), Mayan Export Crude Oil Blend (MECOB) and BRENT oil prices for the period between January 1, 2010 and May 30, 2014.
Empirical results suggest: 1) that each of the analyzed series of stock index and oil returns can be adequately described with the proposed AR (1)-TGARCH model; 2) that a leverage effect exists in the stock index returns and in oil returns: volatility increases when returns fall; 3) that there is linear dependence between the stock index and oil returns, as indicated by the correlation coefficient (36% with MECOB and 25% with BRENT), and a small degree of concordance, as shown by Kendall’s τ (tau); 4) that there is a small degree of conditional dependence in the lower tail and significant degree of conditional dependence on the upper (right) tail.
This last point leads us to conclude that there is a weak, but stable, probability of a decrease in stock returns, following a decrease in oil returns, and a strong positive probability of an increase in stock returns, following an increase in oil returns varying in time. This study indicates that stock market investors expect the stock market to gain, depending on previous earnings, when the oil price increases; on the other hand, when the oil price falls, there is a 50% probability of losses in the stock market.
Finally, for possible future studies, it would be interesting to extend this study to different sectors, and examine this data using different volatility and copula models.











 nueva página del texto (beta)
nueva página del texto (beta)



