1. Introduction
The eastern part of the Mediterranean Sea and its continental areas extend from 18.80-43.5º N and 29.9-41.7º E, including Greece, Turkey, Cyprus, Israel, Lebanon, Egypt, Syria and Libya. The study area (Fig. 1) is economically important, being exploited for fisheries, oil and gas extraction, and offshore renewable energy; it is also used for shipping, which links its many harbors. In the coastal zone, tourism, road transportation, recreation, agricultural and livestock production are major uses. The Mediterranean basin is characterized by strong spatiotemporal contrasts in the precipitation pattern, with high variability at multiple timescales often enhanced by orography, associated with large inter-annual fluctuations and a high heterogeneity of precipitation regimes, terrain, and land surface properties (de Luis et al., 2010; Piras et al., 2016; Cid et al., 2017). The eastern part of Mediterranean area is considered one of the most vulnerable regions to climate change (Giorgi, 2006; IPCC, 2007; Lu et al., 2007; Zittis et al., 2022). The Mediterranean Sea was possibly the first of the world’s seas where changes in temperature were attributed to global warming (Bethoux et al., 1990).
Precipitation and temperature are the most important climatic variables in the hydrology/climate/atmosphere fields and in water resources due to their critical effect on the temporal and spatial patterns of water availability, transpiration, and evaporation. Studies to detect trends in temperature and precipitation series are essential to analyze the impact of climate change in such areas. Several studies have analyzed temperature, precipitation, or extreme temperature-precipitation trends in the Eastern Mediterranean area (Sahsamanoglou and Makrogiannis, 1992; Xoplaki et al., 2004; Kostopoulou and Jones, 2005; Zhang et al., 2005; Kuglitsch et al., 2010; Philandras et al., 2011; Lelieveld et al., 2012; Caloiero et al., 2018; Hafez, 2018; Mathbout et al., 2017), and also sea surface temperature (SST) trends and variability in the Mediterranean basin/sub-basins (Nykjaer, 2009; Shaltout and Omstedt, 2014; Androulidakis and Krestenitis, 2022).
On a national basis, these trends have been addressed by the studies of Pnevmatikos and Katsoulis (2006), Feidas et al. (2007), Philandras et al. (2008), Kambezidis et al. (2010), Nastos et al. (2011), Mamara et al. (2015), Feidas (2017), Tzanis et al. (2019), Kastridis et al. (2022), Sakalis (2022), Varlas et al. (2022), Stathi et al. (2023), referred to Greece; Kadioğlu (1997), Türkeş (1999), Türkeş et al. (2002), Türkeş and Erlat (2003), Partal and Kahya (2006), Hadi and Tombul (2018), Topuz et al. (2020), Mersin et al. (2022), Todaro et al. (2022), Aalijahan et al. (2023), referred to Turkey; Ben-Gai et al. (1999), al-Rimmawi et al. (2010), Givati and Rosenfeld (2013), Shadeed (2013), Yosef et al. (2019), Ajjur and al-Ghamdi (2021), Salameh et al. (2022), referred to Israel; Price et al. (1999), Giannakopoulos et al. (2010), Zaifoğlu et al. (2017), Zittis et al. (2021), referred to Cyprus; and Shaban (2011) and Ramadan et al. (2013), referred to Lebanon.
In some of the above-mentioned studies, yearly teleconnection indices (the North Atlantic Oscillation Index, NAOI, and the Mediterranean Oscillation index, MOI) were both analyzed in accordance with the temperature and precipitation variability on a national basis or within the Mediterranean region/sub-regions.
Although there are numerous studies on a national or regional basis referred to trend detection of the main weather variables, straight comparisons between these are not always representative. One of the main purposes is the examined periods, which differed between each other from some years to more than a decade. Statistical methods for trend detection, such as the non-parametric Mann-Kendal (Mann, 1945) and the Sens slope estimator (Sen, 1968) are affected by the length of the existing data series (Burn and Elnur, 2002). Otherwise, collecting data from weather stations is often a difficult and time-consuming procedure, especially when these stations belong to different countries, and different authorities are responsible for their operation. Additionally, the quality of ground-based weather station series sometimes is low, often with the absence of the relevant metadata and possible data gaps (missing values), relocations, calibration issues, etc., and sometimes homogenization (Gofa et al., 2019) and quality control is needed.
An issue that may affect the accuracy of results in the Eastern Mediterranean basin is the low spatial density of the existing ground-based weather stations that were used in several studies, especially in the mountainous areas of Greece and Turkey, a possibility which led to a range of unknown scale of microclimates. A way to overcome these possible issues is the use of results provided by several existing and reliable weather variables databases, such as the Climate Research Unit Time series (CRU TS) database from the University of East Anglia in the United Kingdom (the current version is 4.05), which covers the global region for the period 1901 to the present (Harris et al., 2020). Relevant data are based on high-quality weather stations, interpolated in 0.5º latitude-longitude grid cells. By using gridded data, climate models can be evaluated more directly since they represent spatial area averages rather than point data; moreover, averaging over regions is straightforward and, finally, estimated data become available for non-observed locations. Several studies have used the CRU-TS datasets for trend detection of climatic variables in the Eastern Mediterranean basin on a national or regional basis, such as those from Philandras et al. (2011), Ramadan et al. (2013), Hadi and Tombul (2017, 2018), and Sakalis (2022).
Accurately predicting trends of precipitation and temperature can play an important role in irrigation scheduling, use of water resources, social planning, human health, production programming, environmental and civil protection, etc. Forecasting methods such as the autoregressive integrated moving average (ARIMA; Box and Jenkins, 1976) are often used to forecast several variables in meteorology, atmospheric physics, hydrology, and also in marketing, economical sciences, trading, human health, epidemiology, medicine, etc. Non-seasonal ARIMA and/or seasonal ARIMA (SARIMA) methods were recently successfully implemented to forecast future precipitation, temperature, or evapotranspiration variables by Soltani et al. (2006), Wang et al. (2014, 2021), Feng et al. (2016), Mahmud et al (2017), Rahman et al. (2017), al-Balasmeh et al. (2019), Coban et al. (2021), and Tadesse and Dinka, (2022).
The aim of the present study is to examine the current trend of annual precipitation and temperature series in the Eastern Mediterranean basin on a national basis, including the annual variability of SST anomalies and the connection effect with the NAOI and MOI. The period under consideration is mainly the last 32 years, from 1990 to 2021. Another interesting feature of the present study is the prediction of monthly and yearly temperature and precipitation series on a national basis for the next four or eight years. In the available literature there is not a recent and complete study obtained on a national basis, that either includes trend detection in common periods, predicted annual and monthly results, and the examination of the correlation with the teleconnection patterns for the Eastern Mediterranean basin. The results of the present study could be of high interest to national authorities and environmental unions/organizations aiming to understand the current and future influence of climate change phenomena, by aiding them to organize and improve the existing corrective actions for reducing its negative effects on the society and environment.
2. Data and methods
2.1 Study area
The study area (Fig. 1) comprises the eastern part of the Mediterranean Sea. Its continental regions extend from 18.80 to 43.5º N and from 29.9 to 41.7º E. The area includes Greece, Turkey, Cyprus, Israel, and Lebanon. The selection criterion for countries that belong to the area under consideration is the percentage (> 30%) of their perimeter washed by the Mediterranean Sea. Based on this criterion, Egypt, Syria, and Libya were excluded from the study. Another reason for this exclusion was that the main territories of these particular states are extended far away from the Eastern Mediterranean (EM) basin and they are mostly affected by different climatic phenomena (Northern Africa and Western Asia areas have a mostly dry climate).
According to the Köppen-Geiger’s climate classification system, the climate of the EM basin (Fig. 1) is characterized mainly as hot-summer Mediterranean climate (temperate Csa, Cfa, Cfb), with the north-eastern parts of Turkey as continental (Dsa, Dfa) and the southern part of Israel as dry (Bwh).
2.2 Historical weather data
2.2.1 Precipitation and Temperature
Country-based long-term monthly precipitation and temperature data records were obtained from the gridded monthly data of the CRU TS v. 4.05 (Harris et al., 2020), downloaded from the Climate Change Knowledge Portal (CCKP, 2021). for the period 1990-2021 (the last 32 years). Considering that data records form CRU TS v. 4. are available from 1901 to the present, and for comparison with the available results of other studies, the period under consideration spans appropriately towards the past.
2.2.2 North Atlantic Oscillation Index (NAOI)
According to Feidas et al. (2007), the North Atlantic Oscillation (NAO) is one of the large-scale modes of climate variability in the Northern Hemisphere. It defines the large-scale meridional oscillation of atmospheric mass between the center of the subtropical high surface pressure located near the Azores and the sub-polar low surface pressure near Iceland.
Strong positive phases of the NAO tend to be associated with above-normal temperatures in the eastern United States and across northern Europe and below-normal temperatures in Greenland and oftentimes across southern Europe and the Middle East. They are also associated with above-normal precipitation over northern Europe and Scandinavia and below-normal precipitation over southern and central Europe. Opposite patterns of temperature and precipitation anomalies are typically observed during strong negative phases of the NAO. During particularly prolonged periods dominated by one particular phase of the NAO, abnormal height and temperature patterns are also often seen extending well into central Russia and north-central Siberia (Walker, 1924; Walker and Bliss, 1932; van Loon and Rogers, 1978; Rogers and van Loon, 1979).
The NAOI data used for the present study were based on Hurrell et. al. (2003), and provided by the Climate Analysis Section of the National Center of Atmospheric Research (https://www.cgd.ucar.edu/sections/cas). The data analyzed span mainly from 1990 to 2021. NAOI data records are available from 1899 to present.
2.2.3 Mediterranean Oscillation Index (MOI)
The MOI has been defined by Conte et al. (1989) and Palutikof et al. (1996) as the normalized pressure difference between Algiers (36.4º N, 3.1º E) and Cairo (30.1º N, 31.4º E). It is described as a teleconnection pattern with opposite pressure and rainfall anomalies between the Central-Western and Eastern Mediterranean areas. It explains the annual precipitation variability across the Central-Western Mediterranean basin better than the NAOI. The MOI is constructed from the 500 hPa surface height monitored by soundings at stations in Algiers and Cairo is often assumed to be representative of the Western and Eastern basin, respectively. When the pressure increases in the Western basin a decrease is found in the East, and vice versa.
The MOI data used for the present study were provided by the CRU, and analyzed mainly for the period from 1990 to 2021. The MOI data records are available from 1948 to the present.
2.2.4 Sea Surface Temperature (SST)
SST data from the Mediterranean Basin based on satellite measurements for the period 1990-2014 were provided by the European Environmental Agency (EEA, 2012). SST data records referred to the Mediterranean basin are available from 1870 to 2014.
2.3 Methodology
2.3.1 Homogeneity test of the data
Meteorological observations are often subject to influences caused by instrument changes or other reasons (i.e., relocation of the observatory, change in the observation times, missing data, methods used to calculate the daily means, and increased urbanized and or industrialized areas), which can introduce artificial trends in time series and render their data unrepresentative of the actual climate variation. The four well-known nonparametric methods selected to test the departure from homogeneity in time series are the standard normal homogeneity test (SNHT) for a single break (Alexanderson, 1986), The Buishand range test (Buishand, 1982), the Pettitt test (Pettitt, 1979) and the von Neumann ratio test (von Neumann, 1941).
The CRU TS v. 4.05 data analyzed in the present study (see section 2.2.1) are based on results from selected weather stations with high quality standards, so the possible detected inhomogeneities could probably occur due to real climatic conditions rather than artificial influences.
2.3.2 Trend detection
The auto-correlated Mann-Kendall test (Mann, 1945; Kendall, 1955; Hamed and Ramachandra, 1998) with Sen’s slope estimator method (Sen, 1968) is used to eliminate the autocorrelation and to verify the presence of a trend in precipitation and temperature time series data. The method was used for annual precipitation and temperature data as well as for SST and NAOI/MOI data.
2.3.2.1 Auto-correlated Mann-Kendall test
The Mann-Kendall test is a nonparametric test for monotonic trend detection. It does not assume the data to be normally distributed and is flexible to outliers in the data. The test assumes a null hypothesis (H 0 ) of no trend and an alternate hypothesis (H a ) of increasing or decreasing monotonic trend. For a time series Xi = x1, x2,..., xn, the Mann-Kendall test statistic S is calculated as
where n is the number of data points, x i and x j are the data values in time series i and j (j > i), respectively, and sign (x j - x i ) is the sign function calculated as
Statistic S is normally distributed with parameters E(S) and variance V(S) as given below:
where n is the number of data points, m is the number of tied groups, and t k denotes the number of ties of extent k. The standardized test statistic Z is calculated using Eq. (4):
To test for a monotonic trend at an α significance level, the alternate hypothesis of trend is accepted if the absolute value of standardized test statistic Z is greater than the Z 1 - α/2 value obtained from the standard normal cumulative distribution tables. A positive sign of the test indicates an increasing trend and a negative sign indicates a decreasing trend.
According to the variance correction approach proposed by Hamed and Ramachandra (1998), recently used by Patakamuri et al. (2020), when the time series exhibit a significant serial correlation, the following modified variance V(S)* of the Mann-Kendall test is used:
The proposed correction factor CF is
where r k and r k R are the lag − k serial correlation coefficients of data and ranks of data, respectively and n is the total length of the series. In the case of the correction factor CF, only significant correlation coefficients are used.
2.3.2.2 Sen’s slope estimator
The Sen’s slope method (Sen, 1968) is a robust nonparametric method of estimating the magnitude of a trend slope. For a given time series Xi = x1, x2,..., xn, with N pairs of data, the slope is calculated as:
Median of N values of βi gives the Sen’s estimator of slope β
2.3.2.3 The (S)ARIMA forecast models
The ARIMA model, one of the Box et al. (1976) methods, is an important statistical approach in forecasting and analyzing time series data related to precipitation and temperature (Soltani et al., 2006; Wang et al., 2014, 2021; Feng et al., 2016; Rahman et al., 2017; Mahmud et al., 2017; al-Balasmeh et al., 2019; Coban et al., 2021; Tadesse and Dinka, 2022). It is more common to label it as ARIMA(p, d, q), where p is the order of the autoregressive process, q is the order of the moving average process, and d is the differentiation process. In general, the ARIMA(p, d, q) model for time series data can be expressed as:
where φ and θ are the autoregressive and moving average parameters, respectively, B is the backward shift operator, Z t the observation at time t, θ the moving average parameter, and εt the residual of the model at time t.
The Seasonal ARIMA model (SARIMA), proposed by Box and Jenkins (1976), was used for model building and forecasting monthly rainfall and temperature. It can be labeled as ARIMA(p, d, q) (P, D, Q), where (p, d, q) is the nonseasonal part and (P, D, Q) is the seasonal part of the model, which could be written as:
where Φ and Θ are the seasonal autoregressive and moving average parameters, respectively, S is the seasonal difference, and
In the present study, the appropriate combination of parameters above was performed in order to choose the best model for all cases, as described in the next section.
The evaluation of methods was performed using the XLSTAT package. Diagrams were performed with the Origin Pro V.8 package.
2.3.2.4 Model performance criteria
The performance efficiency of the predicted models can be evaluated using the statistical indices mean absolute error (MAE), root mean square error (RMSE), and the Nash-Sutcliffe efficiency coefficient (NSE), defined as
where N is the number of the observations, and y i , and are the observed, the predicted and the mean value, respectively.
3. Results and discussion
3.1 Homogeneity test of the data
In the present study, homogeneity tests were performed on both precipitation and temperature data series. The time period in which these tests were implemented is the complete available set of yearly precipitation and temperature of the CRU TS 4.05 data series (from 1901 to 2021). Whenever at least two of the homogeneity tests analyzed in section 2.3.1 detect an inhomogeneity (95% confidence level [c.l.]) in the same year, this year is evaluated as a possible change point of the series (Schonwieseand Rapp, 1997; Wijngaard et al., 2003).
In the case of the CRU TS 4.05 precipitation series, no possible change point was detected, whereas, for the CRU TS 4.05 temperature series, the possible change points (1997 for Greece and 1993 for all the other countries) are presented in Table I. It must be noted that the SST series were also subjected to the homogeneity test, without any possible change point being detected.
Table I Trend detection results for precipitation, temperature series and MOI and NAOI.
| Trend detection results | ||||||
| Period | Year of change point | Mann-Kendal coefficient Z | Significance (p) | Sen’s slope (mm yr-1) | ||
| Precipitation | GREECE | 1990-2021 | 2.29 | (*) | 4.356 | |
| CYPRUS | 1990-2021 | - | 0.76 | 0.223 | 1.523 | |
| ISRAEL | 1990-2021 | - | 0.18 | 0.403 | 0.310 | |
| TURKEY | 1990-2021 | - | 0.73 | 0.203 | 1.121 | |
| LEBANON | 1990-2021 | - | 0.34 | 0.307 | 0.738 | |
| Indices | NAOI | 1990-2021 1955-2021 1955-2013 | - | -0.99 2.57 1.66 | 0.161 (*) (+) | -0.022 0.031 0.014 |
| MOI | 1990-2021 | - | -0.70 | - | -0.001 | |
| Temperature | GREECE | 1990-2021 | 1997 | 4.69 | (***) | 0.047 |
| CYPRUS | 1990-2021 | 1993 | 4.75 | (***) | 0.059 | |
| ISRAEL | 1990-2021 | 1993 | 4.69 | (***) | 0.047 | |
| TURKIE | 1990-2021 | 1993 | 4.65 | (***) | 0.047 | |
| LEBANON | 1990-2021 | 1993 | 4.49 | (***) | 0.047 | |
| SST | 1990-2014 | - | 5.00 | (***) | 0.042 | |
MOI: Mediterranean Oscillation Index; NAOI: North Atlantic Oscillation Index.
Bold characters denote significant trends at a 90% confidence level (+), 95% (*), 99% (**), and 99.9% (***).
According to Hadi and Tombul (2018) 1997 was also detected in their study as a change point in the Turkey temperature series. In the case of Greece, 1997 and 1998 were frequently denoted as years of starting trends by Mamara et al. (2015) and Feidas (2017).
As stated in section 2.3.1, the detected inhomogeneities of the CRU data series could occur due to real climatic conditions rather than artificial influences.
3.2 Precipitation trends
Table I presents the series of annual trend precipitation for the EM region countries, together with the NAOI and MOI. Results are referred mainly to the period 1990-2021. For comparison with the available results of other studies, the period under consideration spans appropriately towards the past for Greece, Israel, Turkey, Cyprus (Table II), and the NAOI (Table I).
Table II Results of annual precipitation and temperature trends compared to other studies available in the literature.
| Present study Literature | ||||||||
| Period | Mann-Kendal coefficient Z | Significance | Trend (Sen’s slope) (mm y-1 or ºC y-1) | Available studies | Trend (mm y-1 or ºC y-1) | Area-averaged data based on | ||
| Precipitation | GREECE | 1955-2001 1951-2009 1950-2020 | -3.39 -2.97 -1.91 | (***) (***) (*) | -3.512 (5.002 % decade-1) -2.23 -1.086 | Feidas (2007) Filandras (2011) Varlas et al. (2022) | (5±2% decade-1) (*) - -1.02 (+) | WS*(22) CRU 3.01 ERA 5 |
| CYPRUS | 1985-2015 | 0.37 | - | 0.916 | Zaifoğlu et al. (2017) | - | WS (37) | |
| ISRAEL | 1950-2009 | -1.18 | (p=0.129) | -0.595 | Givati (2013) | -0.701 (*) | NCEP/NCAR Reanalysis | |
| TURKEY | 1955-2013 | 0.51 | - | +0.354 | Topuz (2020) | +0.9 | W.S (29) | |
| LEBANON | - | - | - | - | - | - | - | |
| Temperature | GREECE | 1979-2017 | (***) | 0.038 | Tzanis et al (2019) | 0.034 (**) | ERA INTERIM Reanalysis | |
| CYPRUS | 1901-2000 | 2.37 | (*) | 0.005 (0.5 ºC century-1) | Price et al. (1999) | (≈1 ºC century-1) | WS (2) | |
| ISRAEL | 1988-2017 | 4.42 | (***) | 0.048 (0.48 ºC decade-1) | Yosef et al. (2019) | (0.53 decade-1) (*) | WS (34) | |
| TURKIE | 1955-1989 | -1.16 | (**) | -0.018 (-0.63 ºC) | Cadioglu (1997) | (-0.81 ºC) | WS (17) | |
| LEBANON | 1963-2009 | 3.83 | (***) | 0.030 (1.38ºC) | Shaban (2011) | (1.8 ºC) | WS | |
W.S* referred to Weather Station.
Bold characters denote significant trends at a 90% confidence level (+), 95% (*), 99% (**), and 99.9% (***).
The annual variation of precipitation series, together with the relative linear trend (Sen’s slope), including the NAOI and MOI, is visualized in Figure 2.

Fig. 2 Precipitation series (a-e) with relative trends (Sen’s slope), (f) NAOI, and (g) MOI during the period 1990-2020. (NAOI: North Atlantic Oscillation Index; MOI: Mediterranean Oscillation Index).
During the period 1990-2021 (Table I), all the observed annual precipitation trends in the EM region are positive, whereas only in Greece the trend is significant at the 95% c.l. These positive annual precipitation trends span form 0.310 mm yr-1 (Israel) to 4.36 mm yr-1 (Greece).
The results of the present study in various periods (Table II) are in close agreement with the results of the available literature referred to gridded monthly data (Givati and Rosenfeld, 2013; Varlas, 2022), and in a general qualitative agreement with the results of Philandras et al. (2011), who based their study on CRU 3.01 gridded data, but did not provide an area-averaged value of the relative trend.
The results of the present study are in general agreement with the result of the available literature referred to area-averaged weather station data (Feidas et al., 2007) and in general qualitative agreement with the results of Zaifoğlu et al. (2017), which are based on 37 weather stations of northern Cyprus (these authors do not provide the area-averaged data). However, the results of the present study (referred to Turkey) are in slight agreement with those of Topuz et al. (2020).
According to the present study, during the period 1990-2021 the observed annual trend of the NAOI (Table I, Fig. 2) is negative but not significant (p = 0.161). This result indicates that during the period 1990-2021, the NAOI trend is weakened, resulting possibly in warmer and wetter conditions within the influenced areas. The increased positive precipitation trend in Greece (2.29 mm yr-1, p = 0.161) and Turkey (0.73 mm yr-1, p = 0.203) during this period could partially be explained by the relative negative trend of the NAOI. The reversing sign of the NAOI trend for the last 30 years is a remarkable observation, in spite of the strong positive trends of the periods 1955-2021 and 1955-2013.
Table III presents the correlation coefficients between the precipitation series of the EM with the NAOI and MOI. The series are referred mainly to the period 1990-2021. Additionally, sub-periods between 1951 and 2020 are also examined for comparison with other studies.
Table III Correlation between the series of temperature and precipitation with NAOI and MOI.
| Correlation between series | ||||||||
| Country | Period | ΝΑΟΙ | MOI | SST* | ||||
| Correlation coefficient (R) | Probability (p) | Correlation coefficient (R) | Probability (p) | Correlation coefficient (R) | Probability (p) | |||
| Precipitation | Greece | 1990-2021 1955-2001 1951-2010 1955-1995 | -0.295 -0.44 -0.373 | 0.101 0.002 0.0033 | -0.268 -0.19 | 0.138 0.230 | 0.50 | 0.011 |
| Cyprus | 1990-2021 1955-2001 | -0.017 -0.193 | 0.929 0.19 | 0.183 | 0.316 | 0.17 | 0.42 | |
| Israel | 1990-2021 1955-2001 1970-2020 | 0.331 0.266 0.214 | 0.065 0.0703 0.132 | 0.237 +0.27 | 0.192 0.059 | 0.24 | 0.26 | |
| Turkey | 1990-2021 1955-2013 | -0.278 -0.40 | 0.124 0.00158 | -0.159 -0.06 | 0.383 0.65 | 0.24 | 0.24 | |
| Lebanon | 1990-2021 1955-2001 | 0.209 -0.045 | 0.251 0.765 | 0.327 | 0.068 | 0.05 | 0.81 | |
| Indices | NAOI | 1990-2014 | -0.29 | 0.17 | ||||
| MOI | 1990-2014 | -0.08 | 0.7 | |||||
| Temperature | Greece | 1990-2021 1951-2007 | -0.19 0.27 | 0.31 0.043 | -0.07 0.063 | 0.71 0.64 | 0.80 | 2*10-6 |
| Cyprus | 1990-2021 | -0.44 | 0.013 | 0.23 | 0.21 | 0.79 | 2.4*10-6 | |
| Israel | 1990-2021 | -0.50 | 0.004 | 0.32 | 0.08 | -0.72 | 5.2*10-5 | |
| Turkey | 1990-2021 | -0.41 | 0.02 | -0.26 | 0.15 | 0.75 | 1.6*10-5 | |
| Lebanon | 1990-2021 | -0.49 | 0.005 | 0.25 | 0.17 | -0.76 | 1.16*10-5 | |
NAOI: North Atlantic Oscillation Index; MOI: Mediterranean Oscillation Index.
Bold characters denote significant trends at a 95% confidence level.
Selected correlation diagrams between NAOI and MOI and the precipitation series are presented in Figure 3.
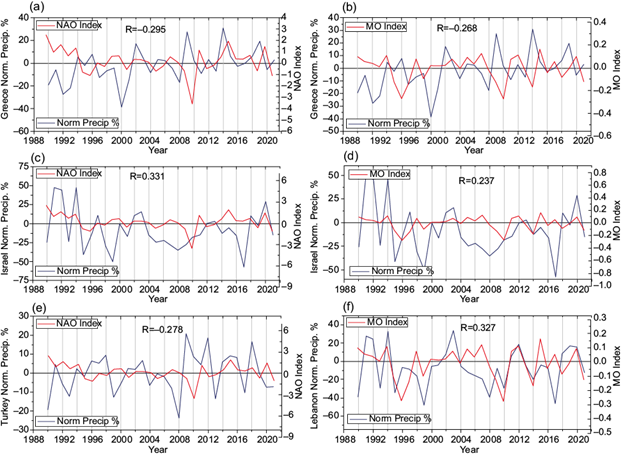
Fig. 3 (a-e) Correlation diagrams between NAOI and MOI, and the precipitation series. (NAOI: North Atlantic Oscillation Index; MOI: Mediterranean Oscillation Index).
Based on the results of Table III and Figure 3, it is observed that during the period from 1990 to 2021, precipitation series form Greece, Cyprus, and Turkey have a negative correlation with the NAOI, whereas Israel and Lebanon have a positive correlation. None of the correlations are significant at the 95% c.l. The MOI has an increased positive correlation with Lebanon’s precipitation series (p = 0.068, non-significant at the 95% c.l.), a slightly increased negative correlation with Greece’s precipitation series (p = 0.138, non-significant at the 95% c.l.), and a slightly increased positive correlation with Israel’s precipitation series (p = 0.192, non-significant at 95% c. l.). As stated by Xoplaki et al (2004) and confirmed by the present study, the NAOI and MOI are not completely independent. For the examined period (1990-2021), the correlation coefficient between them is R = 0.635 (p = 0.00009, highly significant). The correlation between NAOI and Greece’s precipitation (R = -0.44, period 1955-2001) is in close agreement with the result (R = -0.41+/-1) of Feidas et al. (2007) for the same period, and in general qualitative agreement with the result of Philandras et al (2011) for the period between 1951 and 2010. The correlation between the NAOI and Turkey’s precipitation (R = -0.40, p = 0.00158, significant at the 95% c.l., period 1955-2013) differs from the result (R = -0.22, non-significant at the 95% c. l.) of Topuz et al. (2020) for the same period. The correlation referred to the MOI for the same period is also not confirmed by the results of Topuz et al. (2020).
According to Salameh et al. (2022), of the two indices MOI is correlated significantly (R = 0.27-0.38) between 1970 and 2020 with most of the precipitation series based on weather stations inf Israel, which is generally confirmed with the results of the present study (Table II, R = 0.27, p = 0.059) referred to the same period. However, the resulting correlation between MOI and Greece (R = -0.19, p = 0.23 for the period 1955-1995, non-significant at the 95% c.l.) differs gradually from the result (-0.4 ± 0.1, significant at the 95% c.l.) calculated by Feidas et al (2007) for the same period. It should be noted that both the results of Topuz et al. (2020) and Feidas et al. (2007) were referred to weather stations areal-averaged rainfall data.
Another interesting observation based on the last 30-yr period is the reduction of the influence (lower correlation coefficient) of the annual NAOI index (which changes from R = -0.40 to -0.278 from 1955-2013 to 1990- 2021, respectively, and from R = -0.44 to -0.295 from 1955-2001 to 1990-2021, respectively) in the Turkish and Greek territories. Taking the precipitation series of Greece as an example, this means that during the period from 1955 to 2001, 44% of the total rainfall could be explained by the relative NAOI, whereas this amount is reduced to 29.5% from 1990 to 2021.
The mean annual SST anomalies in the Mediterranean region have been studied to assess their simultaneous relationship with the EM ground-based annual precipitation. The correlation between mean annual SST anomalies and precipitation series (Table II) is generally positive but significant (at a 95% c.l.) only regarding the precipitation series of Greece (R = 0.50, p = 0.011). However, this single significant correlation seems to be temporary and is valid only for this examined period; however, no significant correlation is valid during the sub-periods 1960-2014, 1970-2014, and 1980-2014 (results are not presented in Table II). As a result, the Mediterranean annual SST anomalies did not govern the precipitation anomalies in the neighboring continental regions, except for the Greece territory, between 1990 and 2014.
3.3 Temperature trends
Table I also presents the trend of annual temperature series in the EM region, together with mean annual SST anomalies in the Mediterranean region. Results in Table II refer mainly to the period from 1990 to 2021 and other common periods for comparison. The annual variation of the series together with the relative linear trend (Sen’s slope) are visualized in Figure 4.
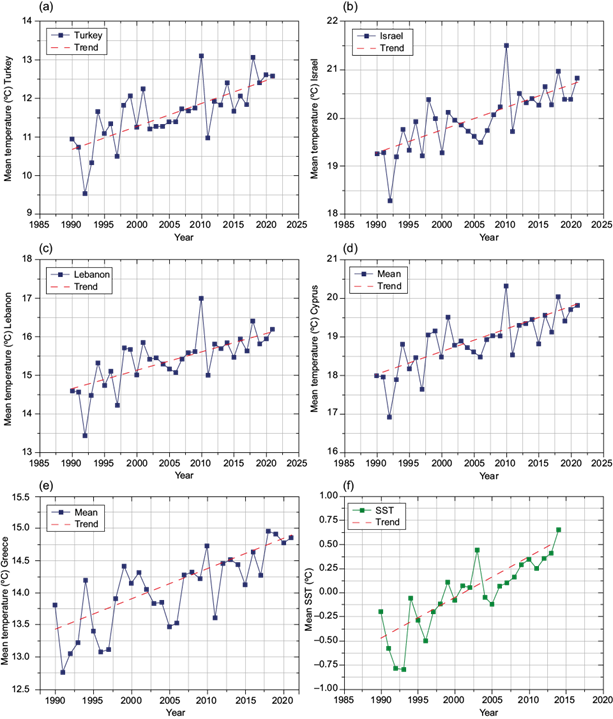
Fig. 4 (a-e) Variations of the mean annual temperature series, (f) mean SST series, together with the relative trend line (Sen’s slope). (SST: sea surface temperature).
Highly significant (at a 99% c.l.) annual temperature trends were detected for all the mean temperature series, including the SST series. These warming temperature trends span between 0.047 ºC yr-1 (Greece, Israel, Lebanon) and 0.059 ºC yr-1 (Cyprus, Turkey).
The results of the present study for annual temperature in various periods (Table II) are in close agreement with results found in the available literature (Tzanis et al., 2019; Yosef et al., 2019) and in general agreement with the results of Kadioğlu (1997), Price et al. (1999), and Shaban (2011). However, the area-averaged value of the trend calculated by Kadioğlu (1997) and Price et al. (1999) may not be representative of the Turkish (based on only 17 weather stations) and Cypriote (based on only two weather stations) territories.
Warming annual trends of the same order of magnitude as those found in the present study were also observed for the SST since 1985 by several studies (Nykjaer 2009; Shaltout and Omstedt, 2014; Androulidakis and Krestenitis, 2022). Selected correlation diagrams between the NAOI and the temperature series (including the SST) are presented in Figure 5.
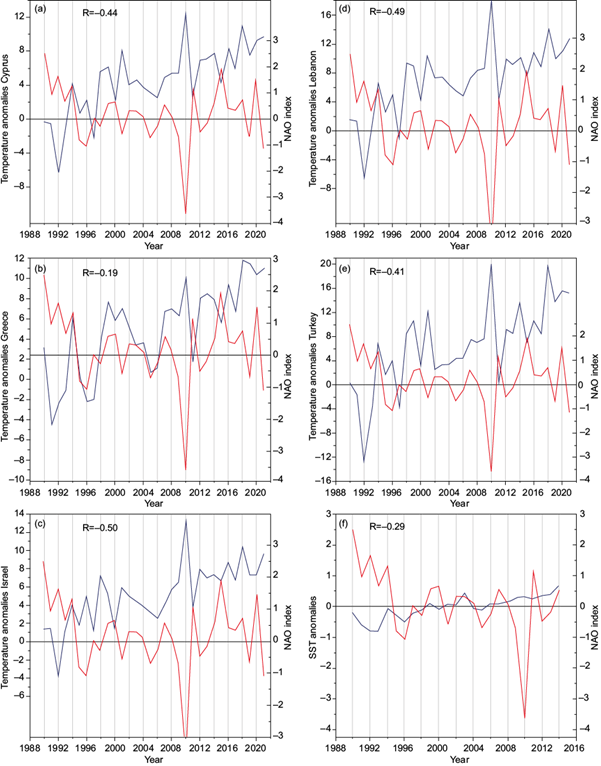
Fig. 5 (a-e) Correlation diagrams between the NAOI and the temperature series, including the (f) SST. (NAOI: North Atlantic Oscillation Index; SST: sea surface temperature).
Significant correlation coefficients (greater than 95% c.l.), during 1990-2021 between the temperature series and the NAOI (except for the series of Greece) were also detected (Table III), in contrast with the relevant results of annual precipitation series. The observed significant correlation coefficients span between 0.41 (Turkey) and 0.50 (Israel). Results in Table III also indicate that the MOI did not play an important role in the annual temperature variation of the EM territory during the period from 1990 to 2021. Regarding the annual SST anomalies, highly significant correlations (greater than 95% c.l.) were observed for all the annual temperature series, ranging between 0.72 (Israel) and 0.80 (Greece). These findings show that between 1990 and 2014, both seawater and land responded synchronously to atmospheric forcing. However, an increasing negative correlation (non-significant at a 95% c.l.) is observed between SST anomalies and the NAOI, whereas almost no correlation is observed between SST and the MOI.
The correlation results of the present study (Table III, Fig. 5) between the temperature series of Greece and the MOI are in agreement with the findings of Nastos et al. (2011), which are mostly positive with non-statistical significance at a 95% c.l. However, in the case of the NAOI, the results of the present study do not confirm the non-significant correlation results of Nastos et al (2011), which significantly are referred to area-averaged temperature based on 29 weather stations within the Greek territory.
Finally, it is worth mentioning that an overall significant or non-significant yearly trend on a national basis does not mean that the regional trend remains the same within the national area. Precipitation trends are relative to several factors, such as the altitude of the region, orientation, distance from the sea, etc. Taking as an example the case of Greece, regional precipitation trends in recent years are mostly stationary, with a few of them positive/negative and significant (Margaritidis, 2021; Sakalis, 2022; Stathi et al., 2023). On the other hand, in the case of temperature, a statistically significant increase in air temperature in recent decades is more pronounced (Proutsos et al., 2020 Kastridis et al., 2022; Stathi et al., 2023). However, the investigation of regional trends is beyond the scope of the present study.
3.4 Forecast results
Several ARIMA and SARIMA models were tested in order to forecast the yearly and monthly precipitation and temperature series for the next four and eight years, respectively. Before the models’ identification, the stationary test of the time series was evaluated by the Kwiatolsky-Philips-Scmidt-Shin (KPSS) (Kwiatkowsky et al., 1992), the Dickey and Fuller (DF) (Dickey and Fuller, 1979), and the Phillips and Peron (PP) (Phillips and Peron, 1988) tests at a 95% c.l. When at least one of these three tests indicated the possible existence of a unit root in the time series, then a model with q = 1 or even 2 was entered in the model test list (differentiation of the time series). The initial models were identified by the inspection of the autocorrelation function (ACF) and partial autocorrelation function (PACF) diagrams. The parameter D of the SARIMA model, which is used for the monthly (seasonal) forecast, was set to D = 12 due to the obvious 12-month periodicity. All the possible combinations using several values of p, q and P, Q were examined in order to determine the best model. The model that gave the best combination of minimum RMSE (Eq. [12]) and MAE (Eq. [11]), the minimum value of the AIC criterion (Akaike, 1994), and the highest Nash-Sutcliffe efficiency coefficient (NSE; Eq. [13]) was selected as the best-fit model (Table III). At the end of the procedure, the identification of the shape of the ACF and PACF functions of the residuals was essential (Fig. 6). When the majority of the ACF and PACF functions lie within the confidence limits, this indicates that there is no significant correlation among them. Regarding yearly forecasts, the period 1990-2020 is used as training period and 2021-2028 as the forecast period. Considering that the yearly values of 2021 are already known, this year is used as validity check of the models. In the case of monthly (seasonal) forecasts (SARIMA models), the years 2021-2024 were used as forecast period and the monthly values of 2021 were used for validation of the seasonal models.
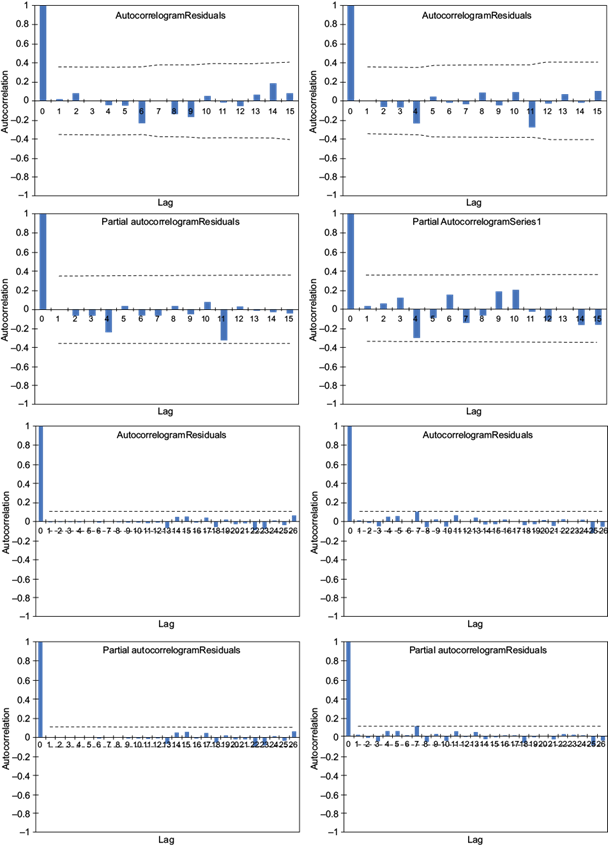
Fig. 6 Selected autocorrelograms and partial autocorrelograms of the models’ residual: (a) ARIMA (15,0,2) for Israel precipitation series, (b) SARIMA (2,0,7) (5,1,2) for Turkey precipitation series, (c) ARIMA (24,2,5) for Lebanon temperature series, and (d) SARIMA (1,0,0) (3,1,1) for Greece temperature series. (ARIMA: autoregressive integrated moving average; SARIMA: seasonal ARIMA).
3.4.1 Precipitation
According to Table IV, of the five selected ARIMA models (one for each country) referred to the yearly forecast of the training period, the MAE ranges from 12.93 to 65.13 mm yr-1, with a mean value of 30.67 mm yr-1, while the RMSE ranges from 17.76 to 76.52 mm yr-1 (mean: 37.62 mm yr-1) and the NSE from 0.76 to 0.919 mm yr-1 (mean: 0.87 mm yr-1).
Table IV Efficiency of the ARIMA and SARIMA models.
| Country | (S)ARIMA | MAE 1980-2020 | RMSE 1980-2020 | NSE 1980-2020 | SD* (2021) | MAE* (2021) | MAE*/SD* | SD (2021) | RMSE (2021) | RMSE/ SD | MAE (2021) | MAE/ SD | R (2021) | |
| Precipitation | Greece | (2,0,6) (5,1,2) | 23.57 | 30.6 | 0.386 | 104.2 | 40.7 | 0.39 | 49.0 | 29.66 | 0.50 | 24.51 | 0.61 | 0.84 |
| Cyprus | (2,0,6) (5,1,2) | 16.36 | 26.51 | 0.648 | 110.5 | 129 | 1.17 | 44.4 | 20.39 | 0.32 | 14.20 | 0.41 | 0.916 | |
| Israel | (2,0,1) (3,1,1) | 10.336 | 17.68 | 0.66 | 76.8 | 8.8 | 0.11 | 30.8 | 13.22 | 0.25 | 7.66 | 0.43 | 0.895 | |
| Turkey | (2,0,7) (5,1,2) | 14.67 | 19.43 | 0.53 | 63.5 | 60.5 | 0.95 | 28.6 | 17.08 | 0.47 | 13.45 | 0.60 | 0.80 | |
| Lebanon | (2,0,5) (7,1,2) | 22.53 | 36.54 | 0.712 | 159.7 | 89.94 | 0.56 | 68.7 | 22.26 | 0.24 | 16.34 | 0.32 | 0.95 | |
| Greece | (24,1,5) | 22.59 | 29.10 | 0.919 | 104.2 | 192.6 | 1.85 | |||||||
| Cyprus | (15,2,2) | 26.76 | 34.20 | 0.901 | 110.5 | 142.58 | 1.29 | |||||||
| Israel | (15,0,2) | 25.93 | 30.48 | 0.834 | 76.8 | 143.66 | 1.87 | |||||||
| Turkey | (24,2,6) | 12.93 | 17.76 | 0.919 | 63.5 | 2.611 | 0.04 | |||||||
| Lebanon | (16,0,2) | 65.13 | 76.52 | 0.76 | 159.7 | 11.84 | 0.07 | |||||||
| Temperature | Greece | (1,0,0) (3,1,1) | 0.8212 | 1.070 | 0.976 | 0.59 | 0.1012 | 0.17 | 6.89 | 0.877 | 0.12 | 0.79 | 0.13 | 0.9916 |
| Cyprus | (6,0,3) (6,1,5) | 0.826 | 1.075 | 0.972 | 0.72 | 0.0384 | 0.05 | 6.39 | 1.007 | 0.15 | 0.931 | 0.16 | 0.987 | |
| Israel | (1,0,0) (3,1,2) | 0.780 | 0.995 | 0.962 | 0.62 | 0.080 | 0.13 | 5.1 | 0.710 | 0.12 | 0.622 | 0.14 | 0.99 | |
| Turkey | (1,0,0) (0,1,2) | 0.969 | 1.263 | 0.976 | 0.76 | 0.054 | 0.07 | 8.11 | 0.962 | 0.10 | 0.837 | 0.12 | 0.993 | |
| Lebanon | (1,0,0) (0,1,5) | 0.849 | 1.092 | 0.971 | 0.68 | 0.0036 | 0.01 | 6.42 | 0.849 | 0.11 | 0.696 | 0.13 | 0.991 | |
| Greece | (23,2,5) | 0.166 | 0.225 | 0.85 | 0.59 | 0.327 | ||||||||
| Cyprus | (23,2,4) | 0.253 | 0.329 | 0.782 | 0.72 | 0.301 | ||||||||
| Israel | (23,1,12) | 0.127 | 0.165 | 0.928 | 0.62 | 0.04 | ||||||||
| Turkey | (23,2,5) | 0.284 | 0.37 | 0.76 | 0.76 | 0.452 | ||||||||
| Lebanon | (24,2,5) | 0.239 | 0.32 | 0.77 | 0.68 | 0.258 |
SARIMA: seasonal autoregressive integrated moving average; MAE: mean absolute error; RMSE: root mean square error; NSE: Nash-Sutcliffe efficiency coefficient; SD: standard deviation; R: Correlation coefficient.
MAE*, SD*, and MAE, SD refer to yearly and monthly values, respectively.
Forecasted results in bold type may have issues of acceptance.
The MAE between forecasted and measured values in 2021 ranges from 2.611 (Turkey) to 192.6 mm yr-1 (Greece), with an average of 98.7 mm yr-1. Despite the sufficient accuracy of the precipitation forecast referred to the training period, the validation of the models in 2021 indicates medium accuracy, owing to the high variance of the precipitation series. According to the NSE criterion (Eq. [13]), values between 0.0 and 1.0 are generally viewed as acceptable levels of performance, with a value of 1 being the optimal. Providing the division of MAE and RMSE with the standard deviation of the observed data (Table IV), stricter criteria may occur. According to this, values of MAE/SD and RMSE/SD less than 0.65 may be considered low and acceptable (Singh et al. 2005; Moriasi et al., 2007; Margiorou et al., 2022). Based on the criteria analyzed before, ARIMA forecasted results for Greece, Cyprus, and Israel may be recognized as non-acceptable (underlined values in Table IV). The same order in accuracy results (referred to the R and the RMSE parameters) is observed in other studies (Mahmud et al., 2017; Wang et al., 2021). The appropriateness of the yearly ARIMA models for forecasting precipitation is partly confirmed.
Regarding the SARIMA models, the MAE of the monthly forecast of the training period indicates a mean value of 22.01 mm yr-1, the RMSE a value of 31.97 mm yr-1 and the NSE is 0.59. The mean values of the MAE, RMSE and correlation coefficient (R) between the forecasted monthly values and the true existing value of 2021 are 15.23, 20.52, and 0.88 mm yr-1, respectively. According to the criteria of MAE and RMSE divided by de SD of the observed data, forecasted results based on SARIMA for Turkey and Cyprus may not be acceptable (higher than 0.65) for yearly precipitation (bold values of Table IV). However, all the monthly forecasted results of the SARIMA model were sufficiently higher than the acceptance values. These results confirm the general appropriateness of the seasonal (SARIMA) models in monthly forecasting. It should be noted also that the accuracy of the forecasted results of the validation period (12 months of the year 2021) are slightly higher than in the training period. Another interesting result is the ability of the SARIMA model to forecast the yearly precipitation of 2021 (average MAE value: 65.79 mm yr-1) better than the relevant ARIMA model (98.7 mm yr-1). Finally, the overall performance of the seasonal SARIMA models seems to be higher than the non-seasonal ARIMA models.
Table V presents the values of the average yearly rainfall during the period from 2022 to 2024, based on the SARIMA model. It is observed that between the period 2022-2024 and the reference period 1990-2021, the average forecasted precipitation is increased by 76.53, 24.72, and 10.26 mm yr-1 for Greece, Turkey, and Cyprus, respectively, and reduced by 22.16 and 2.54 mm yr-1 for Israel and Lebanon, respectively.
Table V Averaged yearly precipitation and temperature forecast values between 2022 and 2024 based on SARIMA models.
| Country | Average 1990-2021 | Predicted average 2022-2024 | Predicted average 2022 | Predicted average 2023 | Predicted average 2024 | |
| Precipitation (mm yr-1) | Greece | 683.81 | 760.64 | 762.574 | 747.242 | 772.086 |
| Cyprus | 456.39 | 466.65 | 494.32 | 435.152 | 470.47 | |
| Israel | 265.52 | 243.36 | 192.061 | 261.95 | 256.825 | |
| Turkey | 598.78 | 623.50 | 624.108 | 614.163 | 632.22 | |
| Lebanon | 652.16 | 649.32 | 704.092 | 610.53 | 633.336 | |
| Temperature (ºC) | Greece | 14.04 | 14.73 | 14.70825 | 14.73217 | 14.73375 |
| Cyprus | 18.86 | 19.68 | 19.66 | 19.71 | 19.67 | |
| Israel | 19.97 | 20.67 | 20.65 | 20.68 | 20.69 | |
| Turkey | 11.62 | 12.49 | 12.48 | 12.49 | 12.49 | |
| Lebanon | 15.37 | 16.11 | 16.08 | 16.13 | 16.11 |
SARIMA: seasonal autoregressive integrated moving average.
The observed and predicted rainfall data, based on ARIMA and SARIMA, are visualized in Figures 7 and 8, respectively.
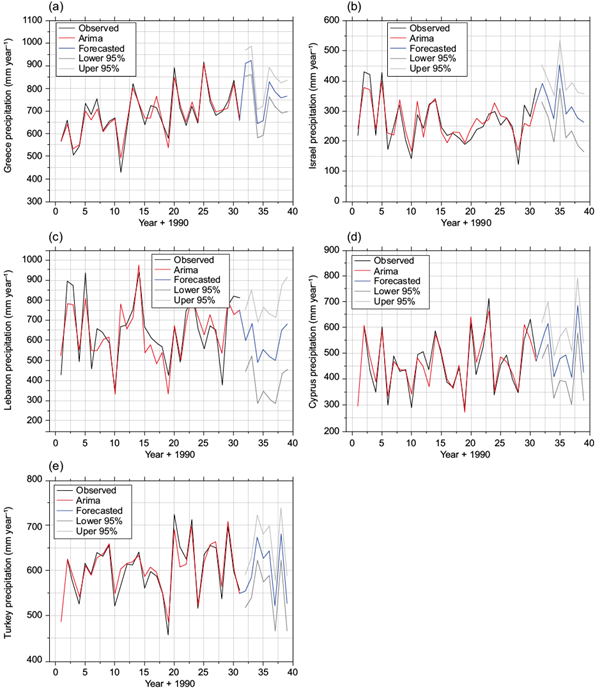
Fig. 7 (a-e) Observed precipitation data, and ARIMA predicted and forecasted data for the period 1990-2028. (ARIMA: autoregressive integrated moving average).
3.4.2 Temperature
The MAE, RMSE, and NSE of the five selected ARIMA models referred to the yearly forecast of the training period indicate a mean value of 0.214, 0.28, and 0.82 ºC, respectively. Correspondingly, the MAE between the forecasted and measured values of the year 2021 ranges from 0.04 and 0.452 ºC for Israel and Turkey, respectively, with an average of only 0.276 ºC (Table III).
Regarding the SARIMA models, the MAE and the RMSE of the monthly forecast of the training period indicate mean values of 0.849 and 1.099 ºC, respectively, and NSE of 0.972. The mean values of the MAE, RMSE and correlation coefficient (R) between the forecasted and measured monthly values of the year 2021 are 0.775 ºC, 0.881 ºC, and 0.991, respectively. As it is indicated in the case of the precipitation forecast, the accuracy of the forecasted mean temperature of 2021 by the seasonal SARIMA model (average MAE: 0.056 ºC) is better than the relevant ARIMA model (0.19 ºC), and the accuracy of the forecasted results of the validation period (12 months during 2021) is slightly higher than in the training period. Based on the NSE criteria, both the ARIMA and SARIMA models used for temperature forecasting are acceptable based on the criteria of MAE/SD and RMSE/SD (Nash and Sutcliffe., 1970; Singh et al., 2005; Moriasi et al., 2007; Margiorou et al., 2022). The overall performance of the seasonal SARIMA models seems to be higher than the non-seasonal ARIMA models.
It is obvious that the ARIMA and SARIMA models used for the prediction of the average temperature are more efficient and reliable than the relevant models used for precipitation, mostly due to the lower variance of temperature series as compared to precipitation series.
The plot of the observed and predicted annual temperature verified that ARIMA models (Fig. 9) and SARIMA models (Fig. 10) are generally appropriate for forecasting.
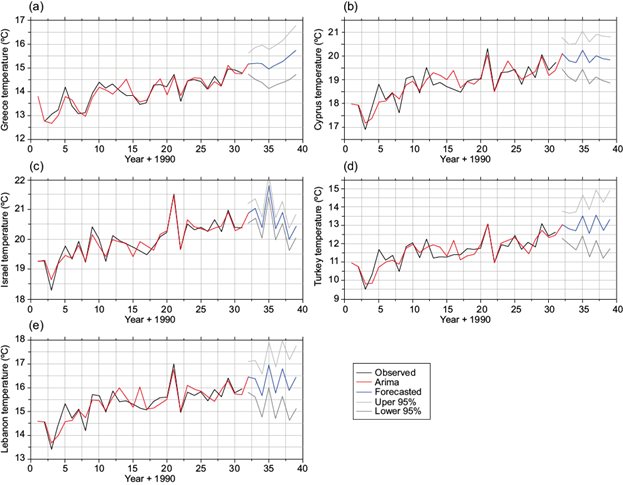
Fig. 9 (a-e) Temperature data: observed, predicted with ARIMA, and forecasted for the period 1990-2028. (ARIMA: autoregressive integrated moving average).

Fig. 10 (a-e) Temperature data: observed, predicted with SARIMA, forecasted, and real (2021) for the period 1990-2024. (SARIMA: seasonal autoregressive integrated moving average.)
Finally, based on Table V the average forecasted temperature between the periods 1990-2021 and 2022-2024 is increased by 0.69, 0.87, 0.7, 0.74, and 0.82 ºC for Greece, Turkey, Israel, Lebanon, and Cyprus, respectively.
4. Conclusions
Temperature and precipitation are of the most interesting weather variables affected by climate change. In the EM region under consideration, only positive trends were observed for precipitation series on a national basis during the period from 1990 to 2021. Between them, the positive trend of Greece is the only significant one at a 95% c.l. These increasing positive trends were observed mostly during the last two decades. During the period from 1990 to 2021, the annual NAOI trend weakened, resulting possibly in warmer and wetter conditions in the influenced areas. The increased positive precipitation trend in Greece and Turkey during this period could be partially explained by the relative negative trend of the NAOI, which led to warmer and wetter conditions. The reversed negative sign of the NAOI trend during the last 30 years is a remarkable observation, in spite of the strong positive trends of the periods from 1955 to 2021 and from 1955 to 2013. None of the examined countries has a significant correlation with the NAOI. The MOI has a strong positive and significant correlation (95% c.l.) only with the Lebanon precipitation series and a slight correlation with the Greece and Israel series. Although Greece and Turkey are sufficiently large countries in order to study their influences based on large-scale circulation patterns, the limited areas referred to Lebanon, Cyprus, and Israel may indicate a possible loss of consistency in response to circulation patterns.
The Mediterranean annual SST anomalies do not govern the precipitation anomalies in the neighboring continental regions, except for the Greek territory during the period from 1990 to 2014.
Highly significant (at a 99% c.l.) annual temperature trends were detected for all the available mean temperature series, including the SST series, during the period from 1990 to 2021. Significant correlation coefficients (greater than 95% c.l.) during 1990-2021 between the temperature series and the NAOI (except for the series of Greece) were also detected, in contrast with the relevant results of annual precipitation series. According to the observed significant correlation between temperature series and the SST, it is observed that the annual mean SST of the Mediterranean region is driven by the ground-based mean annual temperature of the EM and vice-versa. The MOI did not play an important role in the temperature variation of the EM territory during the period from 1990 to 2021 (correlation is not observed).
Despite the different types of weather data used in this and other relevant studies (gridded CRU, ERA5, ERA interim, NCEP/NCAR reanalysis, or ground-based weather station data), the results of the present study are mostly in agreement with the available results found in the literature.
The influence of climate change in the EM seems to be higher regarding mean annual temperature (including the SST) as compared to mean annual precipitation. However, several relatively extreme indices need to be considered in order to document a complete study.
Based on this study and compared to the results found in the available literature, the (S)ARIMA models are appropriate in general for forecasting future temperature and precipitation. Especially, forecasted results based on temperature series indicate higher efficiency (NSE, MAE/SD, RMSE/SD, and coefficient R) than the results of precipitation series. For all the series under consideration, the forecast results of the SARIMA model, referred both to precipitation and temperature in the validating year (2021), are more accurate than the relevant non-seasonal ARIMA models.
Despite the satisfactory accuracy of the predicted precipitation results of the non-seasonal ARIMA models referred to the training period, the models’ validation in the validating year (2021) is sometimes unacceptable, mostly due to the high variance of the precipitation series compared to the temperature series, and also due to the nature of the problems. The single year (2021) used for the validation of the non-seasonal ARIMA models could give an appropriate order of magnitude of the model’s accuracy. However, in the present study, it is imperative to wait for a longer validation period in order to reach more definite and safe conclusions. On the other hand, the validation period of the relevant SARIMA models (12 months) is supposed to be sufficient to extract safer conclusions referred to the departure from the real values.
Finally, it should be mentioned that cases in which an accurately validated ARIMA or SARIMA model does not lead to equivalent accurate relevant forecasted results, are often observed in the available literature. This means that such cases are representative of the limit of the ability of the ARIMA/SARIMA models to produce accurate and reliable forecasts. As a result of these possible issues, several advanced ARIMA models or even different methods (ANN, decomposition, spectral methods, etc.) are already being used by the scientific community to enhance the accuracy of the interesting but difficult and complicated problem of forecasting.
A possible improvement of the present study, which is the analysis of trend detection of temperature and precipitation on a seasonal basis, could be an interesting subject, especially because seasonal large-scale circulation patterns (winter and summer NAOI and MOI) have generally more pronounced climate forcing than annual large-scale circulation patterns. The patterns in winter and summer may depend on different factors, and if their annual average deviates from a long-term average it may not be related to any significant climate forcing and could be the result of pure coincidence.











 nueva página del texto (beta)
nueva página del texto (beta)




