Maximum daily precipitation in Iran (1979-2018)

Poorkarim, Roya; Asakereh, Hossein; Martín-Vide, Javier; Poorkarim, Roya; Asakereh, Hossein; Martín-Vide, Javier

doi:10.20937/atm.53326

Servicios Personalizados

Revista

Articulo

Indicadores

Citado por SciELO
Accesos

Links relacionados

Similares en SciELO

Otros
Otros

Permalink

Atmósfera

versión impresa ISSN 0187-6236

Atmósfera vol.38 Ciudad de México 2024 Epub 07-Oct-2024

https://doi.org/10.20937/atm.53326

Articles

Maximum daily precipitation in Iran (1979-2018)

Roya Poorkarim¹^*

Hossein Asakereh¹

Javier Martín-Vide²

^¹Department of Geography, University of Zanjan, 45371-3879, Zanjan, Iran.

^²Department of Geography, University of Barcelona, 08001, Barcelona, Spain.

ABSTRACT

This article deals with daily precipitation intensities. The maximum daily precipitation values were calculated for return periods of 10, 20, 50, and 100 years using the daily precipitation levels recorded at 42 meteorological stations between 1979 and 2018. Three extreme value probability distribution adjustments were used to do this: Weibull, Generalized Extreme Value, and Gumbel. While all fit the annual maximum daily rainfall series well, Weibull produces lower values than the other two distribution methods. The results show considerable differences between the Caspian fringe in the north, with values reaching 300 mm in Ramsar for a return period of 50 years, and some of the more arid eastern areas of the country, where values were less than 40 mm. An area near the Strait of Hormuz in the south was also identified as having high values. The maximum daily precipitation correlates positively with the annual total and negatively with altitude.

Keywords: generalized extreme value; Gumbel; Iran; maximum daily precipitation; spatial patterns; Weibull

RESUMEN

Este artículo trata sobre las intensidades de la precipitación diaria. Se han calculado los valores de precipitación diaria máxima para periodos de retorno de 10, 20, 50 y 100 años utilizando los valores en un año de precipitación diaria máxima de 42 estaciones meteorológicas para el periodo 1979-2018. Con este fin se han utilizado los ajustes a tres distribuciones de probabilidad de valores extremos: Weibull, GEV y Gumbel. Mientras todas las distribuciones ajustan bien las series anuales de precipitación diaria máxima, la de Weibull da valores más bajos que las otras dos. Los resultados muestran unas diferencias considerables entre la franja del Mar Caspio, en el norte, con valores que alcanzan los 300 mm en Ramsar para un periodo de retorno de 50 años, y algunas de las áreas orientales más áridas del país, con valores inferiores a 40 mm. Un área cercana al estrecho de Hormuz, en el sur también presenta valores altos. La intensidad diaria está correlacionada positivamente con el total anual y negativamente con la altitud.

1. Introduction

The current rising temperature increases evapotranspiration from the land and sea into the atmosphere, and the warmer air can hold more water vapor. Ultimately, we can expect to see more precipitation on a global scale because the water cycle has been intensified and there is more water in motion. Therefore, in some regions, rainfall intensity has already increased or may do so in the future (^{Gordon et al., 1992}; ^{Dourte et al., 2015}; ^{Myhre et al., 2019}, among others).

The intensity of precipitation constitutes the climatic variable that best evaluates the hazard of extreme precipitation or heavy rainfall. This hazard, combined with the vulnerability of society and the exposure of the territory, expresses the risk as a comprehensive concept, for example, the risk from flooding to human systems (^{Reisinger et al., 2020}). Heavy rainfall and subsequent flooding continue to be one of the most economically damaging hazards, with frequent and numerous human casualties. Ninety-one percent of meteorological, climatic, and water hazard deaths occur in developing countries (^{WMO, 2023}).

In the context of climate change and determining the current climate, the global spatial patterns of precipitation prove of great interest to ^{Monjo and Martín-Vide (2016)}. However, the negative impacts of climate change need finer spatiotemporal analysis scales, especially given that they disproportionately affect poorer people in less developed countries who are more vulnerable because of their high dependence on natural resources and limited capacity to cope with climate variability and extremes (^{Adedeji et al., 2014}). The relationships between climate change and intense precipitation have been mentioned in many studies, such as ^{Kappus et al. (1978)}, Trenberth (²⁰⁰⁸, ²⁰¹¹), ^{Asakereh (2014)}, ^{Tramblay et al. (2012)}, ^{Tabari (2020)}, ^{Asakereh et al. (2021)}, and ^{Asakereh and Ashrafi (2023)}. In addition, some studies have analyzed the effect of extreme precipitation on the population (^{Zhang and Zhou, 2020}; ^{Liu et al., 2020}; ^{Kang et al., 2021}), while others have considered the effects on the economy (^{Bauer et al., 2018}; ^{Liu and Song, 2019}) or vegetation (^{Pei et al., 2021}; ^{Zeppel et al., 2014}).

Precipitation is a highly variable climatic element in terms of space and time, typified by contrasting spatial patterns and high annual, seasonal, and monthly coefficient of variation values. As some studies have shown, these patterns also occur in Iran (^{Darand, 2014}). Rainfall variability within Iran is complex, with unpredictable fluctuations from year to year and region to region (^{Modarres, 2006}; ^{Amiri, 2007}). In Iran, sudden and heavy precipitation is one of the environmental hazards most responsible for human and economic losses (^{Mostafaii et al., 2016}), with most of the rainfall occurring during the cold season in the majority of the country (^{Rafiaei et al., 2014}).

Many studies have analyzed precipitation intensity using statistical probability functions. For example, in Asia, ^{Deka et al. (2009)} used five extreme value distributions to create an annual maximum daily rainfall series for northeast India, and ^{Ghosh et al. (2016)} used the Generalized Extreme Value (GEV) distribution and the Gamma Distribution for monthly rainfall data in Bangladesh, among others.

Considering the importance of rainfall in a country’s climate, and especially the variable of precipitation, the main goal of this research was to estimate the return period of the maximum daily values of rainfall in Iran using statistical methods. These daily values constitute an indicator of the intensity of precipitation in places where there are few hourly (or in shorter-time intervals) meteorological records, as is the case of the study at the level of the entire country.

2. Objective and methodology

The main objective of the research is to calculate the maximum daily precipitation for different return periods using data from the best meteorological stations in Iran. The specific objectives are (1) the selection and quality control of the best daily maximum precipitation series of the country, (2) calculating the maximum daily precipitation for different return periods using three statistically appropriate probability distributions, and (3) analyzing the spatial patterns of maximum daily precipitation for different return periods. We must select the probability distributions that best fit the annual maximum daily precipitation series to do this. These series are formed by the highest daily precipitation for each year during the analysis period. After fitting many probability distributions, three continuous probability distributions, Weibull, GEV, and Gumbel Max, were eventually selected (Table I). The calculations were made using Easy Fit, a data analysis program developed by Math Wave Technologies that provides more than 50 probability distributions, and the maps were drawn using a geographic information system (ArcGIS).

Table I Probability distribution functions of the three selected probability distributions.

Distribution	Probability density function
Weibull	f(x) = (α/β)(x/β)^α-1exp(-(x/β)^α)
Generalized extreme value (GEV)	f(x) = (1/σ) exp(-(1 + kz)^-1/k) (1 + kz)^-1-1/k , k ≠ 0 f(x) = (1/σ) exp(-z - exp(-z)), k = 0 where z = (x-μ)/σ
Gumbel Max	f(x) = (1/σ) exp(-z-exp(-z)) where z = (x-μ)/σ

The Gumbel, ^{Weibull (Weibull, 1939}), and GEV distributions, among others, have been widely used to model annual maximum daily precipitation (^{Koutsoyiannis, 2003}; ^{Nadarajah, 2006}; ^{Shukla et al., 2010}; ^{Boudrissa et al., 2017}; ^{Olivera and Heard, 2018}; ^{Back and Bonfante, 2021}; ^{Tahir et al., 2021}, etc.), although some were initially intended to represent the distribution of other variables. Spearman’s correlation coefficient, ρ, is a nonparametric measure of rank correlation (statistical dependence between the rankings of two variables). The Spearman correlation between two variables is similar to the Pearson correlation between the rank values of two variables. It can be calculated using Eq. (1):

ρ =1-[(6∑di2)/nn2-1] (1)

where d is the difference between the two ranks of each observation, and n is the number of observations.

The value of ρ always lies between -1 ≤ ρ ≤ 1. If y increases when x increases, we say they have a positive or direct correlation. If y decreases when x increases (or vice versa), we say they are negatively or inversely correlated. Spearman’s ρ will be used to correlate the extreme daily values with altitude and annual precipitation for a return period.

3. Study area and data

Iran is located in Southwest Asia between 45º-64º E and 25º-40º N. It covers an area of about 1 648 000 km² and has a population of 84 million (Fig. 1). It lies in an arid and semi-arid region with an average precipitation of about 250 mm year^-1. The influence of the Siberian air mass coming from the northeast of Iran, the Mediterranean air mass from the northwest, the Sudanese air mass from the southwest, and the monsoon from the southeast explain the varied climatic conditions of the country. Rainfall is higher in the winter and autumn. As a result of these climatic conditions, and especially the rainfall distribution, most of Iran’s forests are located in the north of the country.

Fig. 1 Location of Iran.

Iran has two large mountain ranges, the Alborz and the Zagros. The Alborz range stretches from west to east to the south of the Caspian Sea, while the Zagros range stretches from northwest to southeast. Damavand, the highest peak in the Alborz range, is 5610 masl, and Dena, the highest peak in the Zagros Mountain range, is 4409 masl.

For this study, the daily maximum precipitation data for each year and every station run by the Iran Meteorological Organization (IMO) were extracted. The information is of good quality and complete, with 40 years of data from 42 stations. Analyses were performed for the 40-year period between 1979 and 2018. Figure 2 and Table II show the location and geographical coordinates of the meteorological stations in Iran.

Fig. 2 Map of Iran with the location of the meteorological stations used.

Table II Meteorological stations and their geographical coordinates

Station	Longitude	Latitude	Elevation (m)	Station	Longitude	Latitude	Elevation (m)
Abade	52º 37’	31º 10’	2030	Island Kish	53º 58’	26º 30’	32
Abadan	48º 18’	30º 20’	606	Mashhad	59º 37’	36º 15’	1065
Ahvaz	48º 37’	31º 17’	10	Noshahr	51º 29’	36º 39’	-20.9
Arak	49º 40	34º 18’	1708	Urmia	45º 03’	37º 32’	1315.9
Ardabil	48º 17’	38º 14’	1332	Qazvin	49º 58’	36º 23’	1297
Babolsar	52º 39’	36º 42’	-21	Ramsar	50º 38	36º 55’	-20
Bam	58º 20’	29º 07’	1066.9	Rasht	49º 32’	37º 15’	-8
Bandar Abbas	56º 14’	27º 23’	9	Sabzevar	57º 39’	36º 14’	977.6
Bandar Anzali	49º 28’	37º 30’	-20.9	Sanandaj	46º 58’	35º 17’	1373.4
Bandar Lenge	54º 53’	27º 49’	22.7	Saqqez	46º 36’	36º 15’	1522.8
Birjand	59º 17	33º 04’	1444	Semnan	53º 21’	35º 48’	1130
Bojnord	57º 07’	37º 30’	1086	Shahrekord	50º 50’	32º 31’	2060
Esfahan	51º 40’	32º 46’	1571	Shahrood	54º 59’	36º 19’	1380
Fasa	53º 37’	28º 56’	1288.3	Shiraz	52º 31’	29º 45’	1519
Gorgan	54º 26’	37º 51’	13.3	Tabriz	46º 14’	38º 06’	1361
Hamadan	48º 29’	34º 58’	1741.5	Tehran	51º 24’	35º 42’	1190
Kashan	51º 25’	33º 59’	982.3	Torbat Heydariyeh	59º 12’	35º 03’	1450.8
Kerman	57º 00’	30º 15’	1760	Yazd	54º 22’	31º 53’	1273.2
Kermanshah	47º 02’	34º 31’	1374	Zabol	61º 29’	31º 09’	489.2
Khoram Abad	48º 16’	33º 35’	1347	Zahedan	60º 32’	29º 29º	1344
Khoy	44º 57’	38º 42’	1103	Zanjan	48º 30’	36º 39’	1663

4. Results

4.1 Maximum daily precipitation for a 10-year return period

The maps in Figure 3 show the maximum daily precipitations at the Iranian stations for a 10-year return period. The values were calculated using the GEV, Gumbel Max, and Weibull probability distributions.

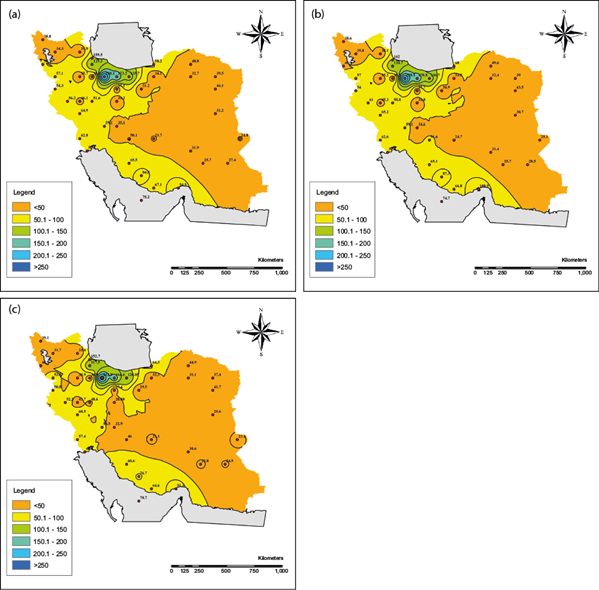
Fig. 3 Daily maximum precipitation for a 10-year return period with the (a) Generalized Extreme Value, (b) Gumbel Max, and (c) Weibull distributions.

The results from all three methods indicate that eastern and central areas of Iran have the lowest maximum daily precipitation, while the area with the highest maximum daily precipitation is in the north of the country. The lowest value obtained by the GEV distribution was 23.7 mm at the Yazd station in the center of Iran. The highest value obtained with the same probability distribution was 230.1 mm in Ramsar on the Caspian coast (west Mazandaran province). The Gumbel Max distribution gives similar values to those obtained by the GEV distribution, with slight differences. However, the values calculated by the Weibull distribution are lower than those returned by the other two throughout the country, with the minimum value of 21.1 mm being obtained for the Yazd station in the center of the country and the maximum value obtained in Ramsar.

4.2 Maximum daily precipitation for a 20-year return period

The maximum daily precipitations at the Iranian stations for a 20-year return period are shown in the maps in Figure 4. Values were calculated using the GEV, Gumbel Max, and Weibull probability distributions. The three probability distributions returned maximum values for the stations in the north of Iran between the Alborz mountains and the Caspian Sea, with maximum daily precipitations of more than 100, 200, and even greater than 250 mm, according to the first two methods. High values were also returned for the Strait of Hormuz between the Persian Gulf and the Oman Gulf in the south, with values above 100 mm for some stations. The lowest values of less than 50 mm correspond to large areas in the country’s east, center, and northwest corner. Using the GEV distribution, the lowest and the highest values were 29.6 and 270.1 mm, respectively. Using the Gumbel Max distribution, they were 29.5 and 264.5 mm at Yazd and Ramsar, the same minimum and maximum locations identified for the 10-year return period. The Weibull distribution returned significantly lower values of 23.8 and 234.3 mm, in the same locations.

Fig. 4 Daily maximum precipitation for a 20-year return period with the (a) Generalized Extreme Value, (b) Gumbel Max, and (c) Weibull distributions.

4.3 Maximum daily precipitation for a 50-year return period

The maximum daily precipitations at the Iranian stations for a 50-year return period are shown in the maps in Figure 5. The values were calculated using the same three probability distributions. All returned maximum and minimum values at the same stations as the 10- and 20-year return periods. The maximum rainfall values were found in the north and south of the country, near the Caspian Sea and the Strait of Hormuz, respectively. The GEV and Gumbel Max methods returned a value in excess of 300 mm in the north. The lowest values were located in the east, with some being less than 40 mm. Compared to the previous return periods, the Weibull distribution produced lower values for all the stations, with the value for Yazd city being just 26.8 mm. For all the distribution methods, the values calculated for the northeast of Iran were not as low as those calculated for the 10- and 20-year return periods.

Fig. 5 Daily maximum precipitation for a 50-year return period with the (a) Generalized Extreme Value, (b) Gumbel Max, and (c) Weibull distributions.

4.4 Maximum daily precipitation for a 100-year return period

The maximum daily precipitations at the Iranian stations for a 100-year return period are shown in the maps in Figure 6. The values were calculated using the same three probability distributions, producing similar spatial patterns to those shown for the other return periods. The maximum rainfall is still observed in the north and south of the country. The maximum daily precipitation calculated by the GEV distribution reaches 366.5 mm in Ramsar, slightly lower than the 346.0 mm returned by the Gumbel Max distribution for the same location. For the area around the Strait of Hormuz in Bandar Abbas, the first distribution method gives almost 200 mm. The lowest values are located in the center and east of the country, with less than 50 mm returned by both the GEV and Gumbel Max distributions for several stations. The Weibull distribution gives lower values in all cases. The minimum precipitation calculated by the GEV is 41.2 mm at the Bam station in Kerman province, while the minimum values calculated by the Gumbel Max and Weibull distributions are in the Yazd province.

Fig. 6 Daily maximum precipitation for a 100-year return period with the (a) Generalized Extreme Value, (b) Gumbel Max, and (c) Weibull distributions.

4.5 Correlation between annual precipitation and maximum daily values

Spearman’s rank correlation method was used to investigate the relationship between annual precipitation values and maximum daily values obtained by the GEV distribution method for a 10-year return period. The results show that Spearman’s ρ is 0.597, sig = 0.000. Therefore, the correlation is positive and statistically significant (Fig. 7a).

Fig. 7 Scatter plots between (a) annual precipitation and maximum daily values estimated with the Generalized Extreme Values (GEV) distribution for a return period of 10 years and (b) altitude and maximum daily values calculated with the GEV distribution for a return period of 10 years.

4.6 Correlation between altitude and maximum daily values

Another question that arises is whether the maximum daily precipitation in Iran increases or decreases with altitude. We used Spearman’s rank correlation coefficient to investigate the relationship between the stations’ altitude and the maximum daily values obtained by the GEV distribution method for a 10-year return period. Spearman’s ρ is -0.377, sig = 0.14. Therefore, the correlation is negative and statistically significant (Fig. 7b). Nevertheless, the figure shows two groups of stations: those at lower altitudes closer to the sea level and those at higher altitudes. The first group has a mix of stations with high intensity (areas around the Caspian Sea and the Strait of Hormuz) and low maximum daily. A slight tendency for the stations at higher altitudes to experience higher intensities can be observed in the second group.

5. Discussion and conclusions

Rainfall is one of the most important climatic variables. It plays a vital role in agriculture, ecosystems, water planning, etc., especially in dry regions and countries like Iran. By studying its climatic characteristics, such as inter-annual variability, seasonal distribution, spatial patterns, and daily maximum, we gain a more comprehensive overview of the phenomenon beyond the average or mean values. Understanding maximum daily precipitation is critical because of its possible adverse effects on soil erosion, floods, and water supply, among others. In this study, the daily precipitation records for 1978-2018 from 42 meteorological stations positioned all over Iran were used to calculate maximum precipitation values for return periods of 10, 20, 50, and 100 years. The calculations were made using three different statistical methods: the probability distributions of Weibull, Generalized Extreme Value (GEV), and Gumbel. These three distributions have been used to adjust the annual maximum daily rainfall series in many regions (^{Koutsoyiannis, 2003}; ^{Singh et al., 2012}; ^{Boudrissa et al., 2017}).

The GEV distribution gives the highest values for all the return periods. Gumbel’s estimates are slightly lower than those obtained using the GEV method, but Weibull’s estimates are considerably lower than both. A comparison between the three probability distributions for flooding in a Moroccan river also found that Weibull produced the lowest estimates, but unlike this study, the Gumbel results were higher than those obtained by GEV (^{Zellou and Rahali, 2017}).

The highest daily precipitation maximum daily was detected in Ramsar in the north of Iran, located on the Caspian coast (west Mazandaran province) and the windward-facing north flank of the Alborz Mountain range that forms a barrier between the south of the Caspian Sea and the Iranian plateau. Using the GEV distribution, the values for Ramsar were 230, 270, 300, and 366 mm day^-1 for return periods of 10, 20, 50, and 100 years, respectively. Moist winds from the Caspian Sea and the rise of air caused by orography probably explain the high annual maximum daily precipitations in this area (^{Ghosh et al., 2016}). In the Mazandaran province, floods are relatively frequent (^{Moradi, 2001}; ^{Yarahmadi and Mryanji, 2011}).

The GEV distribution method identifies additional nuclei of high values in the Persian Gulf close to the Strait of Hormuz, with almost 200 mm. This high value coincides with that obtained by ^{Kappus et al. (1978)}.

The maximum daily precipitation reduces from the west to the east. East Iran is characterized by a hot and arid climate, with the Lut desert (or Dasht-e-Lut) located in the southeast. The minimum daily values were obtained in the Yazd province, with less than 25 mm for a return period of 10 years and a little over 40 mm for a century.

Therefore, in Iran, there is a vast difference between the maximum daily values for different return periods in the Caspian fringe, in the north, and an area near to the Strait of Hormuz, in the south, and the highly arid central and eastern parts of the country.

The next piece of research will analyze the maximum daily precipitation trends for different return periods using the Weibull distribution, as ^{Zhang and Zhou (2018)} did for China between 1961-2011 and ^{Kamari and Noori (2016)} did for the Kermanshah province in western Iran.

Acknowledgments

We thank the EXE (PID2020-116860RB-C21) project led by the Spanish Ministry of Science and Innovation, the Climatology Group of the University of Barcelona (2017 SGR 1362), and the Iran Meteorological Organization (IMO).

References

Adedeji O, Reuben O, Olatoye O. 2014. Global climate change. Journal of Geoscience and Environment Protection 2: 114-122. https://doi.org/10.4236/gep.2014.22016 [ Links ]

Amiri R. 2007. Analysis and Prediction of Precipitation in the city of Khorramabad using Markov chain model. Master’s Thesis, Tehran University of Teacher Training (In Persian) [ Links ]

Andrade T, Rodrigues H, Bourguignon M, Cordeiro G. 2015 The exponentiated generalized Gumbel distribution. Revista Colombiana de Estadística 38: 123-143. https://doi.org/10.15446/rce.v38n1.48806 [ Links ]

Asakereh H. 2012. Frequency distribution change of extreme precipitation in Zanjan City. Geography and Environment Planning Journal 23: 13-18. [ Links ]

Asakareh H, Ashrafi S. 2012. Modeling the number of days of annual precipitation based on relative humidity and annual temperature. Scientific-Research Quarterly of Geographical Data (SEPEHR) 20: 13-17. [ Links ]

Asakereh H, Masoodian SA, Tarkarani F. 2021. A discrimination of roles of internal and external factors on the decadal variation of annual precipitation in Iran over recent four decades (1975-2016). Physical Geographical Research 53: 91-107. https://doi.org/10.22059/jphgr.2021.304776.1007529 [ Links ]

Asakareh H, Ashrafi S. 2023. An investigation into trends in frequency and proportion of different durations of various types of extreme precipitation in Iran. Meteorological Applications 30: e2117. https://doi.org/10.1002/met.2117 [ Links ]

Back ÁJ, Bonfante FM. 2021. Evaluation of generalized extreme value and Gumbel distributions for estimating maximum daily rainfall. Brazilian Journal of Environmental Sciences 56: 654-664. https://doi.org/10.5327/Z217694781015 [ Links ]

Bauer T, Ingram V, De Jong W, Arts B. 2018. The socio-economic impact of extreme precipitation and flooding on forest livelihoods: evidence from the Bolivian Amazon. International Forestry Review 20: 314-331. https://doi.org/10.1505/146554818824063050 [ Links ]

Boudrissa N, Cheraitia H, Halimi L. 2017. Modelling maximum daily yearly rainfall in northern Algeria using generalized extreme value distributions from 1936 to 2009. Meteorological Applications 24: 114-119. https://doi.org/10.1002/met.1610 [ Links ]

Darand M. 2014. Detection of geopotential height changes, vorticity and sea level pressure of prevailing circulation atmospheric patterns impacting Iran climate. Physical Geography Research 46: 349-374. https://doi.org/10.22059/jphgr.2014.52136 [ Links ]

Deka S, Borah M, Kakaty SC. 2009. Distributions of annual maximum rainfall series of north-east India. European Water Resources Association 27: 3-14. [ Links ]

Dourte DR, Fraisse CW, Bartels WL. 2015. Exploring changes in rainfall intensity and seasonal variability in the Southeastern US: Stakeholder engagement, observations, and adaptation. Climate Risk Management 7: 11-19. https://doi.org/10.1016/j.crm.2015.02.001 [ Links ]

Ghosh S, Roy MK, Biswas SC. 2016. Determination of the best fit probability distribution for monthly rainfall data in Bangladesh. American Journal of Mathematics and Statistics 6: 170-174. https://doi.org/10.5923/j.ajms.20160604.05 [ Links ]

Gordon HB, Whetton PH, Pittock AB, Fowler AM, Haylock MR. 1992. Simulated changes in daily rainfall intensity due to the enhanced greenhouse effect: Implications for extreme rainfall events. Climate Dynamics 8: 83-102. https://doi.org/10.1007/BF00209165 [ Links ]

Kamari H, Noori A. 2016. Estimation of rainfall return period using annual rainfall data (case study: Kermanshah city). Quarterly Journal of Research in Science, Engineering and Technology 4: 25-35. [ Links ]

Kang C, Luo Z, Zong W, Hua J. 2021. Impacts of urbanization on variations of extreme precipitation over the Yangtze River delta. Water 13: 150. https://doi.org/10.3390/w13020150 [ Links ]

Kappus U, Bleek JM, Blair SH. 1978. Rainfall frequencies for the Persian Gulf coast of Iran/Les fréquences de pluie pour le Golfe Persique, Iran. Hydrological Sciences Bulletin 23:119-129. https://doi.org/10.1080/02626667809491774 [ Links ]

Koutsoyiannis D. 2003. On the appropriateness of the Gumbel distribution for modelling extreme rainfall. In: Proceedings of the ESF LESC Exploratory Workshop held at Bologna, 303-319. https://doi.org/10.13140/RG.2.1.3811.6080 [ Links ]

Liu Y, Song W. 2019. Influences of extreme precipitation on China’s mining industry. Sustainability: 6719. https://doi.org/10.3390/su11236719 [ Links ]

Liu Y, Chen J, Pan T, Liu Y, Zhang Y, Ge Q, Ciais P, Penuelas J. 2020. Global socioeconomic risk of precipitation extremes under climate change. Earth’s Future 8: e2019EF001331. https://doi.org/10.1029/2019EF001331 [ Links ]

Modarres R. 2006. Regional precipitation climates of Iran. Journal of Hydrology (New Zealand) 45: 13-27. [ Links ]

Monjo R, Martín-Vide J. 2016. Daily precipitation concentration around the world according to several indices. International Journal of Climatology 36: 3828-3838. https://doi.org/10.1002/joc.4596 [ Links ]

Moradi HR. 2001. Synoptic study of flood on November 21, 1996, in central areas of Mazandaran province. Development of Geography Training Magazine (in Persian) 56: 33-41. [ Links ]

Mostafaii H, Alijani B, Saligheh M. 2016. Synoptic analysis of widespread heavy rains in Iran. Journal of Spatial Analysis Environmental Hazards 2: 65-76. [ Links ]

Myhre G, Alterskjær K, Stjern CW, Hodnebrog Ø, Marelle L, Samset BH, Sillmann J, Schaller N, Fischer E, Schulz M, Stohl A. 2019. Frequency of extreme precipitation increases extensively with event rareness under global warming. Scientific Reports 9: 16063. https://doi.org/10.1038/s41598-019-52277-4 [ Links ]

Nadarajah S. 2006. The exponentiated Gumbel distribution with climate application. Environmetrics 17: 13-23. https://doi.org/10.1002/env.739 [ Links ]

Olivera S, Heard C. 2019. Increases in the extreme rainfall events: Using the Weibull distribution. Environmetrics 30: e2532. https://doi.org/10.1002/env.2532 [ Links ]

Pei F, Zhou Y, Xia Y. 2021. Assessing the impacts of extreme precipitation change on vegetation activity. Agriculture 11: 487. https://doi.org/10.3390/agriculture11060487 [ Links ]

Rafiaei A, Alijani B, Yazdani MR. 2014. Synoptic analysis of the onset of the earliest widespread winter precipitation in Iran (except the Caspian Sea coastal region) (in Persian). Iranian Journal of Geophysics 8. [ Links ]

Reisinger A, Howden M, Vera C, Garschagen M, Hurlbert M, Kreibiehi S, Mach KJ, Mintenbeck K, O’Neill B, Pathak M, Pedace R, Portner HO, Poloczanska E, Corradi MR, Sillmann J, van Aalst M, Viner D, Jones R, Ruane AC, Ranasinghe R. 2020. The concept of risk in the IPCC Sixth Assessment Report: A summary of cross-working group discussions. Intergovernmental Panel on Climate Change, Geneva, Switzerland, 15 pp. [ Links ]

Shukla RK, Trivedi M, Kumar M. 2010. On the proficient use of GEV distribution: A case study of subtropical monsoon region in India. Annals. Computer Science Series 8: 81-93. [ Links ]

Singh B, Rajpurohit D, Vasishth A, Singh J. 2012. Probability analysis for estimation of annual one day maximum rainfall of Jhalarapatan area of Rajasthan, India. Plant Archives 12: 1093-1100. [ Links ]

Tabari H. 2020. Climate change impact on flood and extreme precipitation increases with water availability. Scientific Reports 10: 13768. https://doi.org/10.1038/s41598-020-70816-2 [ Links ]

Tahir T, Hashim AM, Takaijudin H, Yusof KW, Osman M. 2021. The best fit probability distribution model for the estimation of extreme rainfall in Limbang, Sarawak. Platform: A Journal of Engineering 5: 39-45. https://doi.org/10.61762/pajevol5iss1art12279 [ Links ]

Tramblay Y, Badi W, Driouech F, El Adlouni S, Neppel L, Servat E. 2012. Climate change impacts on extreme precipitation in Morocco. Global and Planetary Change 82-83: 104-114. https://doi.org/10.1016/j.gloplacha.2011.12.002 [ Links ]

Trenberth KE. 2008. The impact of climate change and variability on heavy precipitation, floods, and droughts. In: Encyclopedia of hydrological sciences. Part 17. Climate change (Anderson MG, McDonnell JJ, Eds.). https://doi.org/10.1002/0470848944.hsa211 [ Links ]

Trenberth KE. 2011. Changes in precipitation with climate change. Climate Research 47: 123-138. https://doi.org/10.3354/cr00953 [ Links ]

Weibull W. 1939. A statistical theory of the strength of materials. Ingeniörsvetenskapsakademiens Handlingar 151. Stockholm: Generalstabens Litografiska Anstalts Förlag. [ Links ]

WMO. 2023. Atlas of mortality and economic losses from weather, climate, and water-related hazards (1970-2021). World Meteorological Organization, Geneva, Switzerland. Available at: Available at: https://unfccc.int/documents/306865?gad_source=1&gclid=CjwKCAjwydSzBhBOEiwAj0XN4PNdaYremCJZHXS0QsbPk4Zw-xiukvPmsW80JtYCl5aNvPoS2O3xgxoCyzgQAvD_BwE (accessed 2024 April 12) [ Links ]

Yarahmadi D, Mryanji Z. 2011. The analysis of dynamic and synoptic patterns of heavy rainfall in the southwest of Caspian Sea and west of Iran (case study: rainfall on 04/11/2004) (in Persian). Physical Geography Research Quarterly 43: 105-120. [ Links ]

Zellou B, Rahali H. 2017. Assessment of reduced-complexity landscape evolution model suitability to adequately simulate flood events in complex flow conditions. Natural Hazards 86: 1-29. https://doi.org/10.1007/s11069-016-2671-8 [ Links ]

Zeppel MJB, Wilks JV, Lewis JD. 2014. Impacts of extreme precipitation and seasonal changes in precipitation on plants. Biogeosciences 11: 3083-3093. https://doi.org/10.5194/bg-113083-2014 [ Links ]

Zhang W, Zhou T. 2020. Increasing impacts from extreme precipitation on population over China with global warming. Science Bulletin 65: 243-252. https://doi.org/10.1016/j.scib.2019.12.002 [ Links ]

Received: August 25, 2023; Accepted: June 21, 2024

^* Corresponding author; email: roya_poorkarim@znu.ac.ir

This is an open-access article distributed under the terms of the Creative Commons Attribution License