1. Introduction
Precipitation estimates are crucial in comprehending the hydrological cycle within specific basins or regions. Their significance spans diverse applications, from facilitating design and planning to predicting outlier events like droughts and floods. Gridded rain gauge estimates have recently witnessed increased demand due to their ability to account for spatial and temporal rainfall distributions. These data primarily serve as inputs for hydrological models integrated with Geographic Information Systems (GIS).
Estimating precipitation in regions with intricate physioclimatic characteristics presents significant challenges due to its spatial and temporal variability. Waylen et al. (1996) employed geostatistics to analyze precipitation estimates and investigate their response to the El Niño phenomenon in the complex terrain of Costa Rica. They discovered that the complexity of precipitation estimation arises from distinct generating mechanisms, topographical influences, oceanic factors, and the lag period considered. Similarly, Holawe and Dutter (1999) explored complex climate patterns in Austria’s mountainous regions on a seasonal scale, gaining valuable insights by comparing the results of simulated wet and dry periods.
Sideris et al. (2020) introduced NowPrecip, a precipitation nowcasting system that operates at various temporal scales by utilizing radar data and an optical flow algorithm based on geostatistics known as NowTrack. They successfully applied this system in the mountainous regions of Switzerland. On a seasonal scale, Portalés et al. (2010) conducted a comparative analysis of univariate and multivariate estimation methods in Valencia, Spain, to develop models for different seasonal periods. Given the geographical heterogeneity, they concluded that no single estimation method suits all scenarios. Notably, seasonal events like heavy rainfall during the wet season significantly impact interpolation, as Giarno et al. (2020) demonstrated.
Meanwhile, Vischel et al. (2009) demonstrated the sensitivity of hydrological systems to precipitation intensity and spatial patterns. Their study explored interannual variability resulting from changes in the precipitation regime over a decadal timeframe, leading to fluctuations in runoff. Notably, runoff estimation showed a significant difference, with kriging yielding 25% lower estimates than those obtained with conditional point simulations. It is widely known that kriging/cokriging type estimates tend to smooth out the data, while simulations, on the other hand, accurately reproduce the variability of the data. However, it has been recognized that estimation and simulation approaches are optimal for criteria that typically conflict with each other (Goovaerts, 2000a). The estimation objective is to minimize the local error variance, while the simulation objective is to reproduce global statistics such as the histogram or semivariogram. On the other hand, according to Webster and Oliver (2007), simulations are not recommended if the main purpose is estimation because the variance of a simulated value is larger than that of a kriged value.
Multivariate geostatistics have proven valuable in dealing with complex climates and terrains. Methods like cokriging (CK) or kriging with external drift (KED) have demonstrated the ability to incorporate secondary information effectively. Notably, when estimating precipitation, incorporating information such as topographic elevation as a covariate has shown promising results, mainly when there is a strong correlation with terrain elevation (Hevesi et al., 1992; Martinez-Cob, 1995; Holawe and Dutter, 1999; Diodato, 2005; Murthy and Abbaiah, 2007; Putthividhya and Tanaka, 2012; Kumari et al., 2017).
Although the outcomes generally favor ordinary cokriging (OCK) (Viola et al., 2010), its implementation can be challenging as it requires fitting a linear coregionalization model (LCM). Using a bivariate data set (precipitation-covariate), LCM requires two direct variograms and one cross variogram, which must be positive definite. Some methods to prove this can be found in Wackernagel (1998) and are used by applications such as ArcGIS-Geostatistical Analyst (Johnston et al., 2001), where cross variograms are calculated through cross covariances in the coregionalization models. In this way, the software adapts these models by allowing a spatial shift between variables, adding two parameters to describe the shift in the x- and y-coordinate. On the other hand, studies such as Hevesi et al. (1992) and Huang and Hu (2009) conclude that OCK variants give better results than kriging as long as the precipitation-covariable correlation is good (> 0.7).
The spatial variability in precipitation patterns is influenced by various environmental descriptors, encompassing both complex terrain and other contributing factors. Researchers such as Goovaerts (2000b) and Subyani and al-Dakheel (2009) suggest incorporating additional secondary variables to enhance the precision of cokriging estimates. Volkmann et al. (2010) have also employed CK and KED alongside radar data as a covariable. Among the various factors explored for their correlation with precipitation, two significant ones are the distance to the shoreline and the topography.
The proximity to coastlines plays a crucial role in precipitation patterns. Ogino et al. (2016) identified distinct precipitation peaks near the coast, gradually diminishing over approximately 300 km on both sides of the coastline. Similarly, Buttafuoco and Lucà (2020) conducted a study in the coastal chain of southern Italy, revealing higher precipitation levels near the shoreline, particularly at higher elevations. Hayward and Clarke (2009) observed a greater variability in precipitation per kilometer near the coast, with certain seasons exerting notable influence in regression models.
Topography also significantly impacts precipitation distribution. Johansson and Chen (2003) delved into the relationship between precipitation, topography, and wind flow in Sweden, as represented by geostrophic air humidity from the shoreline. The results showcased increased variation in the windward zone of the mountain range due to pressure changes with wind speed, while coastal regions experienced rising air, gradually diminishing in mountain valleys.
In a comparative study, Majani et al. (2007) compared KED with ordinary kriging (OK) using topographic elevation, slope, wind, and shoreline distance as covariates. The researchers found that topographic elevation emerged as the most effective covariate, as precipitation correlations with the other variables remained relatively small (< 0.5).
Meanwhile, Cunha et al. (2013) evaluated OCK with topographic elevation and shoreline distance data in Espírito Santo, Brazil, and compared it with OK. The results slightly favored OCK interpolation with topographic elevation, only marginally outperforming shoreline distance.
Spatial distributed pluviometric data is one of the main inputs for hydrological models; therefore, reducing geostatistical estimation error uncertainty is vital to enhance the accuracy of model simulations and projections. The Santiago River basin (SRB) covers a large part of the west coast of Mexico with a wide diversity in relief and climates, which makes pluvial precipitation estimation a challenging problem (Ávila-Carrasco et al., 2016). This study compares the effectiveness of univariate or multivariate geostatistics with shoreline distance or terrain elevation as secondary variables to reduce precipitation estimate error uncertainty. The precipitation estimates are generated for characteristic dry and humid months using OK and OCK. Additionally, the rainfall-covariable correlation and logarithmic transformation benefits are explored for both cases.
2. Data and methodology
2.1 Study area
The SRB is located in the western central region of Mexico, encompassing an area of approximately 76 274 km² with a perimeter spanning 1923.5 km. This basin extends across seven Mexican states, including northern Jalisco, southern Zacatecas, Aguascalientes, and eastern Nayarit, as well as smaller portions of Durango, San Luis Potosí, and Guanajuato (Fig. 1). The SRB culminates in an outflow into the Pacific Ocean near the town of San Blas, Nayarit. Its highest topographical point reaches an elevation of 3130 m above sea level (masl).
Within the Hydrological Region VIII Lerma-Santiago, the SRB is renowned for its remarkable climatic and biomass diversity. This basin is further partitioned into two distinct hydrological subregions: Río Alto Santiago and Río Bajo Santiago. The topography traverses an array of elevations, spanning from sea level along the Pacific coast to the towering heights of 4500 masl in mountainous regions such as the Nevado de Toluca in the State of Mexico and the Nevado de Colima in the state of Jalisco.
Land use within this basin exhibits a range of patterns, with forests occupying 32% of the territory, agricultural areas comprising 27%, jungles constituting 18%, and grasslands and thickets encompassing 14%. The remaining land is distributed among vegetation zones (7%), urban areas, and wetlands (1%).
The SRB’s average surface runoff is about 7849 hm³ yr-1, with an annual water availability of 6287 hm³ yr-1. The basin has 47 overexploited aquifers, leading to a deficit of 216 hm3. Groundwater recharge is 1803 hm³ yr-1, yet the exploitation index averages 0.60.
The basin houses approximately 7 459 130 people across 11 081 localities within 123 municipalities. With a population density of 103 people per km², urban centers like Guadalajara, Aguascalientes, and Tepic house around 87% of the population.
Economically, the 2008 Gross Domestic Product (GDP) amounted to 552 466 411 MXN (at 2003 prices), equivalent to 6.5% of the national GDP. The tertiary sector played a pivotal role, constituting 23.74% of the total GDP of the hydrological region in 2008 (CONAGUA, 2014).
In the northeastern expanse of Lake Chapala, the Poncitlán dam governs the discharge of the principal collector within the SRB. The Santiago River traverses the states of Jalisco, Zacatecas, and Nayarit, journeying 524 km before flowing into the Pacific Ocean. Navigable only by small boats in Nayarit, the Santiago River is punctuated by significant tributaries, including the Verde, Juchipila, Bolaños, and Huaynamota rivers. Several reservoirs within the basin primarily serve irrigation and power generation purposes (Gómez-Balandra et al., 2012).
Per the National Water Commission of Mexico (CONAGUA, 2014), the basin’s climate exhibits arid conditions in the northern sector, while a humid climate characterizes the central region, transitioning into hot and humid conditions along the coast. The annual average precipitation stands at 822 mm year-1, with a notable concentration of 80% occurring between June and September. The basin experiences an average annual temperature of 19 ºC and an evaporation rate of 1831 mm.
2.2 Main characteristics of the rainfall variability in the Santiago River basin
The SRB can be categorized into three distinct physio-climatic regions based on its seasonal precipitation patterns, as Méndez-González et al. (2008) outlined. The first region occupies the northern segment of the basin, extending across the Mexican plateau and encompassing the elevated zones (Fig. 2). This is the most arid region, which witnesses the lowest annual average rainfall, measuring 446 mm. The second region occupies the basin’s central expanse, which is predominantly characterized by the topographic elements of the “Sierra Madre Occidental” mountain range. Here, the average annual precipitation stands at 748 mm. The third region is along the coastal regions of Jalisco and Nayarit in the central sector of the Mexican Pacific. It experiences the highest humidity levels among the three, with an average annual rainfall of 1008 mm.
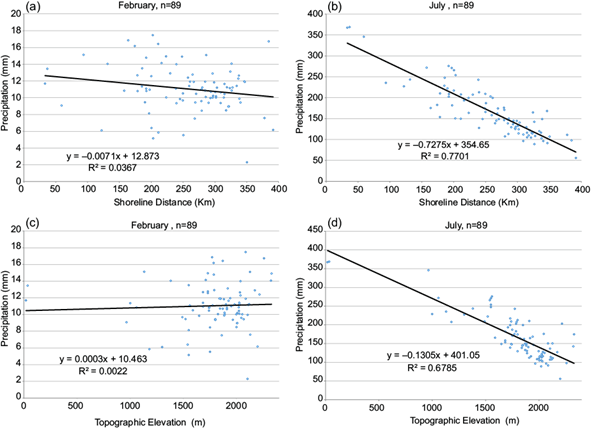
Fig. 2 Correlations between (a) February’s precipitation and shoreline distance, (b) July’s precipitation and shoreline distance, (c) February’s precipitation and topographic elevation, and (d) July’s precipitation and topographic elevation.
The SRB is situated in the tropical zone of the northern hemisphere, specifically south of the Tropic of Cancer. The trade winds and mid-latitude phenomena brought about by oceanic anticyclones dominate this area. Rainfalls occur between May and October, mostly during summer and autumn, which constitute 70% of the yearly rainfall. July receives the highest amount of rainfall, and heat waves are frequent between July and August. Cyclonic disturbances affect the SRB during summer, when the Intertropical Convergence Zone (ITCZ) moves northward. The cyclonic season lasts from June to November, with September and October being the strongest months, accounting for more than half of the yearly rainfall. Winter sees the subtropical high-pressure belt, trade winds moving south, and westerly winds becoming more prevalent. Vortexes and cyclonic depressions occur over the plateau and mountainous regions of the SRB, as they intercept the westerly winds characteristic of mid-latitudes, which bring cold temperatures.
2.3 Rainfall and covariables data
There are 287 meteorological stations in the SRB, with record periods dating back to 1927 and ending in 2010. Only stations that meet specific criteria were selected to ensure consistency in the information collected. Firstly, stations with record periods that start from 1980 or later were chosen. Secondly, only stations with record periods of at least 30 years were considered. Lastly, stations with missing data exceeding 15% of the total monitored data during that period were excluded (CONAGUA, 2014). After applying these criteria, a network of 100 stations with homogenized recording periods ranging from 1980 to 2009 was obtained. The daily data collected over 30 years, equivalent to 10 950 days, was subjected to frequency analysis as a part of the data exploration. This CONAGUA data is freely available through the Climate Computing Project (CLICOM, 2023). Rain gauge spatial locations, CLICOM-ID, and elevations are shown in Figure 1.
The quality of data was improved by applying exploratory data analysis. This involved analyzing mean precipitation for monthly and annual data distribution and checking descriptive statistics, kurtosis, and skewness values. Stationarity and consistency were also checked. Outliers were identified and removed, and data transformation was done to meet requirements. The result was a precipitation set of 89 stations scattered throughout the SRB. Table I shows statistics for selected monthly and annual periods. The dry month statistics are close to normal distribution statistics, but the wet months show significant variation with larger kurtosis and skewness values. This is likely because the dry season has less precipitation than the wet season.
Table I Exploratory analysis of data for 89 rain gauge stations.
| Period | Mean (mm) | Minimum (mm) | Maximum (mm) | Median (mm) | Kurtosis | Skewness | Variance (mm2) | Standard deviation (mm) |
| January | 19.91 | 11.00 | 37.56 | 19.28 | 5.04 | 1.12 | 28.85 | 5.37 |
| February | 11.05 | 2.30 | 17.48 | 10.96 | 3.81 | -0.18 | 7.36 | 2.71 |
| March | 2.79 | 0.75 | 8.50 | 2.76 | 8.02 | 1.39 | 1.37 | 1.17 |
| April | 5.48 | 0.96 | 17.38 | 5.34 | 5.41 | 0.96 | 7.47 | 2.76 |
| May | 18.69 | 5.92 | 29.17 | 18.74 | 3.36 | -0.42 | 22.07 | 4.72 |
| June | 105.09 | 48.72 | 208.33 | 92.35 | 3.11 | 1.00 | 1471.49 | 38.50 |
| July | 167.09 | 55.78 | 368.96 | 149.77 | 4.53 | 1.16 | 3704.12 | 61.11 |
| August | 145.24 | 76.69 | 468.15 | 133.61 | 13.58 | 2.71 | 4260.49 | 65.44 |
| September | 106.01 | 52.47 | 380.78 | 94.19 | 17.75 | 3.37 | 2496.69 | 50.04 |
| October | 40.22 | 24.05 | 149.96 | 36.29 | 23.88 | 4.14 | 309.92 | 17.63 |
| November | 9.74 | 4.71 | 25.19 | 9.06 | 8.74 | 1.75 | 9.59 | 3.10 |
| December | 10.21 | 4.76 | 21.78 | 9.59 | 4.70 | 1.37 | 12.91 | 3.60 |
| Monthly | 53.46 | 28.79 | 129.84 | 48.72 | 7.61 | 1.81 | 325.04 | 18.08 |
| Annual | 641.53 | 345.44 | 1558.09 | 584.70 | 7.61 | 1.81 | 46 806.19 | 216.97 |
Covariable data were available over all the SRB surface. Terrain elevation was provided by the digital elevation model from the Continuo de Elevaciones Mexicano (CEM 3.0). The metadata can be downloaded at the INEGI website (INEGI, 2024). The data used for the SRB surface was in a grid format of 15 × 15 m resolution. On the other hand, for shoreline distance, gridded information was generated for the entire study area surface. A 500 × 500 m grid was generated by getting the shoreline distance to all grid cells using the ArcGIS near (analyst) tool.
3. Geostatistical modeling
Estimates derived from univariate OK and bivariate OCK were compared. The geostatistical approach employed for analyzing each variable encompasses three essential stages: exploratory data analysis, structural analysis, and prediction.
3.1 Exploratory analysis
The exploratory analysis clarifies data characteristics using standard statistical methods. It is vital for all statistical analyses, especially for geostatistics, to ensure data is not affected by distributional or spatial outliers. Inspecting data is the first step in its preliminary exploration to make decisions for addressing any issues with it. This is done by displaying data using histograms, box plots, and scatter diagrams and computing summary statistics (Chilés and Delfiner, 2012).
The sample distribution should be trend-free and exhibit homogenous spatial distribution. When using the OK variance to evaluate local estimate error uncertainty, it is important that the sample distribution is normal-shaped (Heuvelink and Pebesma, 2001). Also, skewed distributions can lead to unstable estimates and less certain inferences (Webster and Oliver, 2007). One way to address this issue is by transforming the measured values to a new scale where the distribution resembles a normal distribution. The physics of the environment might determine what transformation would be appropriate; logarithmic transformations are the most common in Earth sciences.
3.2 Structural analysis
The objective of the structural analysis is to characterize the spatial structure of a regionalized variable. It is the process of estimating and modeling the function that describes the spatial correlation of the variables involved, commonly called the variogram. The reliability of geostatistical estimation depends on the variogram. Univariate kriging spatially estimates a property using known values obtained at neighboring or nearby positions. The function that describes the spatial continuity of the variable is the experimental variogram:
where Z(x i + h) and Z(x i ) are the values of the variables at the points x i + h and x i , respectively. N(h) is the number of data pairs separated by a distance h which in general is a vector. The experimental variogram is fitted with a theoretical variogram model. There are several theoretical variogram models; the most common are spherical, exponential, and Gaussian. The components of a variogram model are the sill, the range, and the nugget.
If two regionalized variables Z v1 (x i ) and Z v2 (x i ) are considered, the cross semivariance moment estimator function is given by the cross-variogram.
A linear coregionalization model (LCM) assumes that all simple variograms (Eq. [1]) and crossed variograms (Eq. [2]) can be expressed as a linear combination of theoretical models (Isaaks and Srivastava, 1989). For the case of considering only two variables, the equations are:
3.3 Model validation
The leave-one-out cross-validation technique was used, which consists of removing one data location and then predicting the associated data using the data in the rest of the locations (Chilès and Delfiner, 2012). The primary use of this analysis is to compare the predicted value with the observed one to provide a rigorous evaluation of a model’s predictive accuracy. The method is applied automatically in ArcGIS Geostatistical Analyst (Johnston et al., 2001). Through the Python tool, the result object contains an entity class (shapefile: line, point, or polygon) and a cross-validation result, including the statistics in Table II.
Table II Summary of prediction error metrics used in cross-validation (Johnston et al., 2001).
| Mean error (ME*): the average difference between the measured and predicted values. |
|
| Root mean square error (RMSE): it indicates the precision of the model to predict the measured values; the smaller this error, the better. |
|
| Average standard error (ASE): the average of the prediction standard errors. |
|
| Mean standardized error (MSE): the average of the standardized errors. This value should be close to 0. |
|
| Root-Mean-Square Standardized Error (RMSSE): its value should be close to one of the valid prediction standard errors. RMSSE >1, the variance in the predictions is underestimated. RMSSE <1, the variance in the prediction is overestimated. |
|
* Z̑(x i ) are predicted values, Z(x i ) are measured values, σ(x i ) is the standard deviation of predicted values, and n is the total data values.
3.4 Ordinary kriging estimator
OK is the most used geostatistical interpolation technique. It is the best unbiased linear estimator because it is based on the minimization of the error variance; it is linear because the estimates are weighted linear combinations of the available information; and it is unbiased because it focuses on obtaining an average residual error equal to zero (Isaaks and Srivastava, 1989). The principle of kriging is to estimate the value of a random variable Z at one or more unmonitored sites or over large blocks, based on more or less scattered data samples such as Z(x 1), Z(x 2),… Z(x N ), at points x 1, x 2,… x N , which can be distributed in two or three dimensions (Webster and Oliver, 2007). The OK theory assumes that the mean is unknown, in such a way that for point estimates the estimate Z̑ at some given position x 0 is given by the following equation:
where λi are the weights that must add up to one to ensure that the estimate is not biased. The local variance of the data within the limits of an ellipsoid is used for the estimation, which is of great help in the case where there are few measurement sites; however, the local variance may not reflect these local changes. In OK, the variance is minimized using an external linear parameter known as the Lagrange multiplier (µ), which minimizes the error and makes the analysis unbiased. In matrix form, this is expressed as follows:
3.5 Ordinary cokriging estimator
The OCK method extends the principles of kriging to accommodate multivariate estimation. It facilitates the prediction of a target variable at a given location by leveraging spatial relationships with neighboring auxiliary or secondary variables that exhibit spatial correlation with the primary variable of interest and offer supplementary information that enhances the accuracy of predictions. In practical applications, OCK is particularly beneficial in areas where data on the primary variable are sparse or unevenly distributed, whereas the auxiliary variables are extensively monitored. One of the most important difficulties of this method is that there are few standard models for cross-covariances or covariograms. A common approach is the linear coregionalization model. However, it is important noticing that cokriging will not always improve the corresponding OK estimate. According to Isaaks and Srivastava (1989), if the primary and secondary variables exist at all data locations and the auto and cross-variograms are proportional to the same basic model, the cokriging estimates will be identical to those of OK. Consequently, if the variogram models demonstrate a high degree of similarity in shape and the primary variable is adequately sampled, the utility of cokriging in improving estimates diminishes.
According to Webster and Oliver (2007), assuming that there are I = 1, 2,…, V secondary variables and the primary variable is denoted as u, then the cokriging predictor for block B, Z̑ u (B) can be expressed as a linear sum:
where the subscript i refers to the sites, of which there are n l where the variable z I has been measured. Furthermore, the estimation variance is minimized by solution of the kriging system (Eq. [12]). In both cases weights λ iL must satisfy Eq. (13) conditions
for all v = 1, 2; . . . , V and all j = 1, 2, . . . ; n v . The quantity γ Iv (x i , x j ) is the (cross-)semivariance between variables I and V at sites i and j, separated by the vector x i x j ; γ̅ uv (x j , B) is the average cross-semivariance between a site j and the block B; and ψv is the Lagrange multiplier for the vth variable. But if I = v or u = v the semivariances are the autosemivariances. Eqs. (12) and (13) give the weights λ that are inserted in Eq. (11) to estimate Z u (B). The estimation variance is given by
where γ̅ uu (B, B) is the integral of γ uu (h) over B, i.e., the within-block variance of u.
Cokriging equations also can be represented in matrix form. For two variables u and v, let Γ uv denote a matrix of semivariances and cross-semivariances between sampling points in a neighborhood. If n u and n v represent places in which variables u and v were measured, the order of the matrix is n u × n v . In the same way, additional Γ uu , Γ vu ¸ Γ vv matrices are generated and included, while b uu and b uv represent the vectors of autosemivariances for variable u and cross-semivariances respectively. In this way, the system of equations in its matrix form is shown as:
Eq. (15) is further simplified as λ = G -1b, where G is the augmented Γ matrix, λ is the vector of weights and Lagrange multipliers, and b is the right-hand vector. The Γ matrix, and the λ and b vectors are not shown in this work; please refer to Webster and Oliver (2007) for the full description.
4. Results
This section begins with an analysis of the variables correlation followed by the exploratory and structural analyses, culminating with the presentation of rainfall estimate results.
4.1 Correlation analysis
The correlation analysis was conducted to support the use of covariates in the estimation with OCK. Estimates of precipitation for a dry month (February) and a wet month (July) were evaluated to represent the wet and dry seasons. Data from 89 rain gauges with records from 1980-2010 were used to obtain these estimates. Figure 2 displays scatter plots of precipitation recorded for February and July against secondary variables: shoreline distance (Fig. 2a, b) or topographic elevation (Fig. 2c, d). Simple linear regression models were fitted using precipitation as the explained variable and covariables as explanatory variables. The coefficient of determination (R2) was used to measure how well the data fit the relationship between the variables analyzed. This coefficient explains the extent to which one factor’s variability can be attributed to its relationship with another related factor. In the linear case, the square root of the coefficient of determination matches with the Pearson correlation coefficient (r), thus measuring the linear dependence between the variables.
Alternatively, the Pearson coefficient also measures the linear relation between two variables; it varies from -1 to +1. Negative values mean that one variable increases while the other decreases, then the fitted line presents a negative slope. A value between ± 0.5 and ±1 is considered a strong correlation. In this case study, a strong correlation is observed for the month of July using both covariates (see Table III). According to Isaaks and Srivastava (1989), a good correlation coefficient may be affected by extreme pairs, resulting in a strong correlation that does not reflect the poor correlation of the other pairs. Alternatively, the Spearman coefficient is a non-parametric test that uses data ranges instead of the original data and is interpreted similarly to the Pearson coefficient. Significant differences between Pearson and Spearman coefficients may provide valuable clues to the nature of the relationship between the two variables. In the results presented in Table III, this is evident when the terrain elevation is used as covariable in both months.
4.2 Exploratory analysis
The selection of final observed data points for estimating rainfall in February and July was informed by these exploratory analyses. Figure 3 illustrates frequency histograms and boxplots depicting precipitation data for February and July. In February (Fig. 3a), the distribution of precipitation appears nearly normal, while a discernible positive bias is evident for July (Fig. 3b). This discrepancy is reflected in a significant difference in the mean precipitation values between the two months. To enhance the normality of the data and mitigate bias in variogram estimation, distributional outliers (values that fall outside boxplot whiskers) were removed from the February dataset, resulting in the retention of 77 rain gauges for analysis (Fig. 3a, c). Additionally, July data underwent transformation using the natural logarithm function (Fig. 3d). The transformed data distribution closely approximates normality, as corroborated by Table IV.
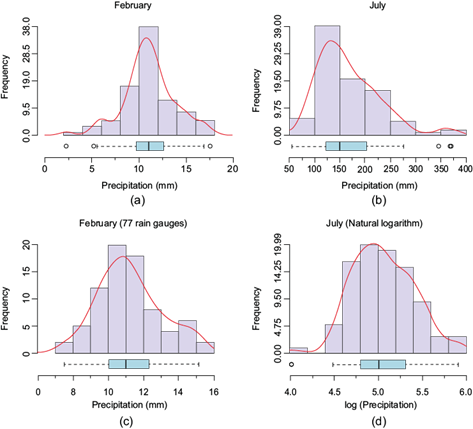
Fig. 3 Frequency histograms for observed precipitation data values of (a) precipitation data for February, (b) precipitation data for July, (c) 77 rain gauges in February removing outliers, and (d) natural logarithm of precipitation data for July.
Table IV Data distribution statistics for July and February and their respective transformed values.
| Statistics | July | Log (July) | February | February (77 rain gauges) |
| Minimum | 55.77 | 4.02 | 2.3 | 7.52 |
| Maximum | 368.96 | 5.91 | 17.47 | 15.13 |
| Mean | 167.09 | 5.05 | 11.05 | 11.20 |
| Standard deviation | 61.10 | 0.34 | 2.71 | 1.79 |
| Skewness | 1.16 | 0.16 | -0.18 | 0.37 |
| Kurtosis | 4.53 | 3.11 | 3.81 | 2.70 |
| 1st quartile | 121.35 | 4.79 | 9.66 | 10.01 |
| Median | 149.77 | 5.00 | 10.96 | 11 |
| 3rd quartile | 204.12 | 5.31 | 2.59 | 12.31 |
| n | 89 | 89 | 89 | 77 |
Also, the data statistics were thoroughly examined. In February, after the removal of outliers, the data from 77 rain gauges exhibited statistics indicative of a closer approximation to a normal distribution. Notably, the kurtosis approached its optimum value of 3, while the mean and median values exhibited greater proximity (refer to Table IV). Similarly, in July, the application of logarithmic transformation yielded statistics that aligned more closely with the desired parameters, as evidenced by Table IV.
Both covariables, terrain elevation, and shoreline distance were available for the entire SRB area, so we selected a grid of observed data points with a separation of 25.69 km for both February and July. Figure 4 shows the selected observed data points used for estimation in February and July. Distributional outliers detected in February appear in red color, while in blue the 77 rain gauges selected for variogram fitting. While for the month of July, all 89 gauges, red and blue, were selected.
During the data exploration process, global trends were identified using the ArcGIS Geostatistical Analyst Trend Analysis (Johnston et al., 2021). These trends and directional influences refer to the deterministic components of a surface that a mathematical formula can represent. This work used a second-order polynomial equation to approximate the valley surface topography. The trend was removed from the measured points, and the analysis was done for the residuals. It was added back in before making predictions. Directional variograms were also examined using ArcGIS-Spatial Analyst. However, no significant variations were found, presenting just omnidirectional variograms.
4.3 Structural analysis
In this work, ArcGIS 10.5 was used to test the best-fitted theoretical variogram model to the dry and humid months data. The best-fit variogram parameters are calculated automatically; then a theoretical variogram is selected based on the cross-validation statistics summary results. To enhance the variogram fitting modification to input data may include outliers removal, logarithmic transformations, and second-degree polynomial trend removal. During the structural analysis of July, logarithmically transformed data was used for better estimations, as highlighted in the exploratory data analysis. The parameter values of the cross variograms for the OCK are summarized in Table V. The acronyms for the different cases are explained in the table's footnote. For example, LSDTR-LP indicates the covariance of the logarithm of the shoreline distance with a second-order trend removal and the logarithm of precipitation. Tables VI and VII follow the same logic. A smaller nugget was observed when the distance to the shoreline was introduced as a secondary variable. When selecting the best option for the bivariate cases for topographic elevation, higher values were noted for the nugget and partial sill despite the use of the same Gaussian model, lag size, and range. Note that for the coregionalization model parameters at bivariate cases, nugget is absent because cokriging uses variogram for autocorrelation and covariance to express cross-correlation (Johnston et al., 2001). The last two lines in Table V provide a comparison between the univariate cases using transformed and untransformed data, with the spherical model being the best fit. Of course, this comparison of bivariate and univariate results was generated by using the same dataset in the application of the respective methods.
Table V Variogram/covariogram parameters used for precipitation data of July.
| Model | Component | Nugget (mm2) | Partial sill (mm2) | Range (m) |
| Gaussian | LP-LP | 0.012 | 0.507 | |
| LSDTR-LSDTR | 0.004 | 0.101 | 470 345.967 | |
| LSDTR-LP | - | 0.001 | ||
| LPTR-LPTR | 0.010 | 0.006 | ||
| Gaussian | LETR-LETR | 0.043 | 0.164 | 93 712.086 |
| LETR-LPTR- | -0.006 | |||
| LPTR-LPTR- | 0.010 | 0.006 | ||
| Gaussian | LSDTR-LSD2TR | 0.001 | 0.026 | 136 213.480 |
| LSD2TR-LP2TR- | -0.001 | |||
| LP2TR-LP2T- | 0.009 | 0.006 | 93 590.645 | |
| Gaussian | SD2TR-SD2TR | 3 469 373.166 | 40 168 869.765 | |
| SD2TR-LP2TR- | -23.129 | |||
| Spherical | P-P | 0.000 | 291.764 | 13 851.708 |
| Spherical | LP-LP | 0.000 | 0.018 | 14 983.725 |
P: precipitation, E: topographic elevation, SD: shoreline distance, L: logarithmic transformation, TR: second-order trend removal.
Table VI shows the structural variogram parameters for February for the bivariate and univariate cases. In most cases, the nugget is large in comparison to the partial sill, which suggests a small spatial dependence of the data. The ratio of the nugget effect to the sill is often referred to as the relative nugget effect and is usually quoted in percentages. For the main variable, when 89 data point values are used, the nugget is 36% of the partial sill; this percentage is increased to 63 % when 77 data points are used (with the outlier values removed). The exploratory analysis of the second variable (not shown) yielded better results after logarithmic transformation, which is why only the logarithmically transformed second variable is presented in Table VI. The models used in the kriging interpolations are shown in the last two lines.
Table VI Variogram/covariance parameters used for precipitation data of February.
| Model | Component | Nugget (mm2) | Partial sill (mm2) | Range (m) |
| Spherical | 89P-89P | 3.650 | 9.155 | 450 824.069 |
| LSD-LSD | 0 | 1.191234 | ||
| LSD-89P | - | -0.103 | ||
| Spherical | 89P-89P | 3.643 | 9.158 | 450 824.069 |
| LE-LE | 0 | 1.713708558 | ||
| LE-89P | - | -0.038 | ||
| Gaussian | 77P-77P | 2.185 | 2.007 | 198 160.691 |
| LE-LE | 0.0486 | 0.590 | ||
| LE-77P | - | -0.072 | ||
| Gaussian | 77P-77P | 2.194 | 2.099 | 207 581.259 |
| LSD-LSD | 0.00041 | 0.411 | ||
| LSD-72P | - | -0.165 | ||
| Spherical | 89P-89P | 2.762 | 7.888 | 262 337.295 |
| Gaussian | 77P-77P | 2.139 | 2.022 | 187 925.888 |
P: precipitation, E: topographic elevation, SD: shoreline distance, L: logarithmic transformation, TR: second-order trend removal.
4.4 Rainfall estimations
Regarding the estimation of rainfall for July, the most accurate results for cross-validation errors are shown in Table VII. Both OCK and OK showed similar results for the root mean squared error (RMSE). However, the univariate OK led to significant underestimation of estimated error variances, particularly in the case of shoreline distance. This is reflected in the average standard error (ASE) of 17.04 in the OK estimation with precipitation data, which was the lowest in comparison with the other cases, conversely to RMSE, which was the biggest (23.45). The best estimates were obtained with OCK by applying a logarithmic transformation to precipitation. This was observed for LPTR-SDTR (see Table VII), where shoreline distance data was used without transformation. The best values for the Root-mean-square standardized error (RMSSE) and ASE were 20.09 and 19.57, respectively, which were slightly superior to the results obtained using topographic elevation (LPTR-LETR) of 20.27 and 19.60, respectively. When comparing the results of transformed precipitation and shoreline distance data (LPTR-LSDTR), stadigraph values were also similar to those of the topographic elevation case, with a slight improvement in error metrics; however, the mean error (ME) was higher.
Table VII Cross-validation results for precipitation of July using OCK and OK
| Stadigraph | Ordinary cokriging | Ordinary Kriging | ||||
| LP-LSDTR | LPTR-LETR | LPTR-LSDTR | LPTR-SDTR | P | LP | |
| ME (mm) | -0.84 | -0.003 | -0.32 | -0.07 | 1.12 | -0.08 |
| RMSE (mm) | 20.22 | 20.27 | 20.44 | 20.09 | 23.45 | 22.83 |
| MSE (-) | -0.061 | -0.013 | -0.025 | -0.015 | 0.04 | 0.01 |
| RMSSE (-) | 1.09 | 1.17 | 1.16 | 1.17 | 1.32 | 1.03 |
| ASE (mm) | 21.64 | 19.60 | 19.59 | 19.57 | 17.04 | 23.31 |
P: precipitation, E: topographic elevation, SD: shoreline distance, L: logarithmic transformation, TR: second-order trend removal.
Figure 5 compares the three best July precipitation estimates and their standard errors for OK and OCK using shoreline distance and topographic elevation as covariates. The figures show the same classes for easy comparison.
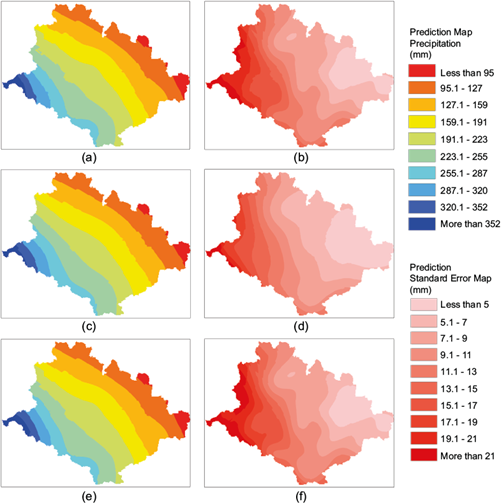
Fig. 5 (a and b) Precipitation estimates and corresponding error maps in July; (c and d) OCK precipitation-topographic elevation (LPTR-LETR) and OCK precipitation-shoreline (LPTR-LSDTR), and (e and f) OCK (LPTR-SDTR) (OCK: ordinary cokriging; L: logarithmic transformation; P: precipitation; TR: second order trend removal; E: topographic elevation; SD: shoreline distance).
The OCK estimates were very similar and had smoother contours, revealing a precipitation gradient with the highest values on the west shore. The most significant differences were in the standard error map using the terrain elevation and the shoreline distance (Fig. 5b, d, f).
When comparing the standard error maps for OCK, the estimates of LPTR-LETR and LPTR-SDTR look quite similar (Fig. 5b, f, respectively). However, LPTR-LSDTR had the highest error expansion near the coast and provided the best result.
All 89 rain gauges were used for the February precipitation estimations, keeping the 77 fitted data variogram parameters. Table VIII displays the three estimation methods’ cross-validation outcomes for precipitation in February. The results indicate that using covariables in OCK resulted in higher RMSEs than univariate OK estimates using the fitted variogram parameters on 77 data. When comparing the errors between 89 and 77 data values, the latter option delivered better results in both bivariate and univariate cases. Despite applying logarithmic transformations to each covariable in OCK estimations, they did not outperform OK results. Reducing the number of gauges from 89 to 77 by discarding distributional outliers for variogram fitting in OK and then adding them back in estimations significantly improved the errors. For instance, ME decreased from 0.005 to 0.0006, RMSE decreased from 2.74 to 2.66, and ASE decreased from 2 to 1.5 in 89 and 77 precipitation gauges, respectively.
Table VIII Cross-validation results for precipitation estimation of February using ordinary co-kriging and ordinary kriging.
| Stadigraph | Ordinary cokriging | Ordinary kriging | ||||
| 89P-LSD | 89P-LE | 77P-LSD | 77P-LE | 89P | 77P | |
| ME (mm) | -0.0038 | -0.0035 | 0.00014 | 0.00085 | 0.0050 | -0.00061 |
| RMSE (mm) | 2.6679 | 2.6682 | 2.6402 | 2.64549 | 2.7418 | 2.6592 |
| MSE (-) | -0.0016 | -0.0015 | 0.00045 | 0.00099 | 0.0016 | 0.00015 |
| RMSSE (-) | 1.2090 | 1.2101 | 1.6588 | 1.6614 | 1.3380 | 1.6807 |
| ASE (mm) | 2.1712 | 2.1696 | 1.5722 | 1.5722 | 2.0084 | 1.5608 |
89P: 89 precipitation gauges, 77P: 77 precipitation gauges, LSD: logarithm of shoreline distance, LE: logarithm of the topographic elevation.
For February, precipitation estimates were compared using the three different methods, similar to what was done in July. The findings showed that the OCK method did not outperform the OK predictions for 77 precipitation gauges. This was due to the limited amount of rainfall recorded during February and the lack of correlation between covariables. According to Goovaerts (2000b), cokriging will be useful as long as a good correlation exists between variables. Therefore, only the best results were mapped and shown in Figure 2a, c, e. To improve the normality of the data, outlier values were removed for variogram fitting (Fig. 3c), although the initial distribution of data was not particularly problematic. Maps were created to display the resulting estimates using OCK for February, based on 77 observed data points and transformed covariables. These maps can be seen in Figure 6a, c. By reducing the data from 89 to 77, the range of variability was narrowed to between 9.1 and 15.2.
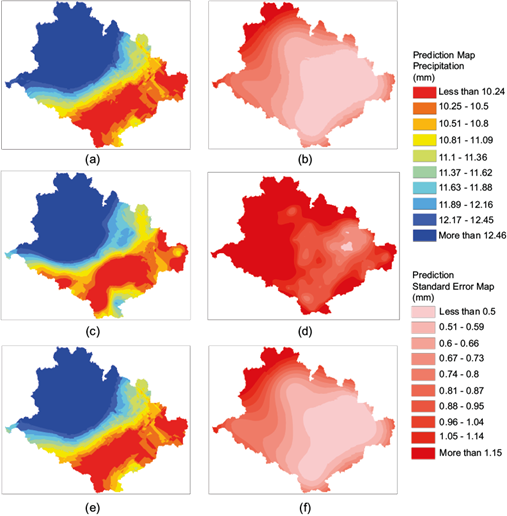
Fig. 6 Left panel, OK estimates for the precipitation of (a) February using the variogram fitted to 77 observed data points and transformed shoreline distance (77P-LSD); (c) OCK using 89 data points and transformed elevation as covariable (89P-LE); (e) using the variogram fitted to 77 observed data points (77P). Right panel, the respective standard errors: (b) 77 observed data points and transformed shoreline distance; (d) OCK using 89 data with transformed elevation as covariable; and (f) using the variogram fitted to 77 observed data points (OK: ordinary kriging; P: precipitation; L: logarithmic transformation; SD: shoreline distance; OCK: ordinary cokriging; E: topographic elevation).
According to Jalili and Modarres (2020), increasing the number of gauges does not necessarily improve estimates. The maps in Figure 6b, d show the standard error predictions, reflecting the uncertainty related to the predicted values. Using 77 data points reduced the estimation error variance from more than 1.37 to less than 0.83. It is important to note that regardless of whether 77 data points or any covariable (elevation or shoreline distance) were used, the contour maps remained the same. Hence, there was no improvement in the estimation.
5. Discussion
Based on the correlation analysis, there seems to be no relationship between the precipitation data for February and the secondary variables. However, for July, the goodness of fit is satisfactory (R² ≈ 0.70) for the two covariates. This justifies the use of the two secondary variables for estimating precipitation with OCK. Logarithmic transformation was used to rectify the precipitation data distribution, which helped to obtain a good fit for July’s precipitation data. This confirms Giarno et al. (2020) findings that data transformations are only beneficial during the wet season and not the dry season in some regions.
In the structural analysis, variogram parameters were analyzed. For the bivariate cases, a Gaussian model was more effective, consistent with the findings of Goovaerts (2000b) and Jalili and Modarres (2020). A larger nugget/sill ratio was obtained when the number of data used to estimate the variogram was reduced. According to Goovaerts (2000a), a larger nugget effect indicates weakened spatial dependence between the two variables’ data, and the benefits of using kriging diminish. Additionally, reducing the number of data points increases the range. The inner points gain weight as the effective range increases, according to Webster and Oliver (2007). Conversely, if the effective range decreases substantially, the weights of inner points decrease while the outer ones increase. A shorter range may produce estimates equal to the mean of the available data, and lower estimation variances due to the differences in the weights become 1 n-1. On the other hand, for larger range estimation, the variance is lower since it produces the effect of samples being twice as close in terms of statistical distance.
The logarithmic transformation of the secondary data, such as shoreline distance and topographic elevations, shows that the RMSSE values are closer to one, indicating a good correspondence between the errors and the estimated error variances. This result coincides with Giarno et al. (2020) findings for the wet season. Other authors, such as Majani (2007) or Cunha et al. (2013), found that terrain elevation provided better results than shoreline distance. However, in the first case, the data did not show a good correlation between shore distance and precipitation, and in the second one, elevation results were only slightly better than those of shoreline distance.
The gradient towards the ocean suggests a strong influence of the humidity source on precipitation. Johansson and Chen (2003) found that rainfall data on the windward side of the mountain range is more variable than in other areas, and terrain slope influence on precipitation is stronger near the coast. This influence is evident in our study zone, where most gauges are in a low variability zone. A rainfall gradient was also detected near the coast, where higher precipitation is recorded, decreasing inland. Similarly, Subyani (2009) found that factors such as shoreline distance and seasonality, apart from terrain elevation and complex terrain, may increase rainfall variability.
6. Conclusions
This study evaluates different techniques for improving precipitation estimation in the SRB, specifically for dry and humid months. Bivariate methods using covariables like altitude and shoreline distance for spatial interpolation of precipitation were compared with univariate methods. Ordinary kriging was used for the univariate case, while ordinary cokriging was used for the bivariate case. Correlation and logarithmic transformation were explored for precipitation data from different seasons, with analysis done for February and July, representing the dry and humid months.
The results showed that estimation improved using transformed data when there was a high correlation between precipitation and covariables for the humid month of July. Using shoreline distance or terrain elevation for spatial estimation using OCK in the wet season months, like July, would be a good option since both covariables showed a good correlation for humid July. Using OCK was justified, and logarithmic transformation helped significantly. This was evident for precipitation and auxiliary variables of terrain elevation and shoreline distance, where data distributions got closer to normal. The improvement was evident, especially for shoreline distance, where errors approached those obtained with terrain elevation.
As is well known, humidity sources, along with terrain elevation, influence the rainfall regime. In this case study, shoreline distance data may offer the same benefits as terrain elevation for geostatistical precipitation estimation in areas like the SRB. Finding the correct geostatistical interpolation algorithm may be difficult since each region is unique due to physiographic and climatological differences. However, following the steps and methods used in this paper could be helpful in achieving good performance for a hydrologic model, thus preventing high costs and biases.
On the other hand, our findings highlight that data transformation and the use of secondary data may not yield satisfactory results during dry months. It is important to note that the normal distribution of data is not a common characteristic of dry months, which poses a challenge for geostatistical methods. Consequently, simpler techniques like the inverse ditance weighted interpolation (IDW) method or Thiessen polygons, which do not rely on data normality assumptions, might be more appropriate in such scenarios. Additionally, while data distribution skewness can be improved by discarding outliers and, therefore, a better variogram fitting is achieved, these data should not be discarded at estimation. Hence, further research is warranted to explore alternative approaches and enhance our understanding of precipitation estimation during dry periods.











 nueva página del texto (beta)
nueva página del texto (beta)




