SciELO - Scientific Electronic Library Online
 
 número127Distribución y condición sexual de las Pottiaceae (Bryophyta) en MéxicoInfluencia de la disponibilidad de luz y la masa de semillas sobre la germinabilidad y el crecimiento inicial de dos especies congénitas de Fabaceae índice de autoresíndice de materiabúsqueda de artículos 		Home Pagelista alfabética de revistas  

Servicios Personalizados

Revista

Articulo

Indicadores

Links relacionados

  • No hay artículos similaresSimilares en SciELO

Compartir

Acta botánica mexicana

versión On-line ISSN 2448-7589versión impresa ISSN 0187-7151

Act. Bot. Mex  no.127 Pátzcuaro  2020  Epub 07-Oct-2020

https://doi.org/10.21829/abm127.2020.1717 

Research articles

Non-destructive method for estimating leaf area of Erythroxylum pauferrense (Erythroxylaceae) from linear dimensions of leaf blades

Método no destructivo para estimar el área foliar de Erythroxylum pauferrense (Erythroxylaceae) a partir de las dimensiones lineales de las láminas foliares

João Everthon da Silva Ribeiro1  3 
http://orcid.org/0000-0002-1937-0066

Ester dos Santos Coêlho2 
http://orcid.org/0000-0002-5541-1937

Francisco Romário Andrade Figueiredo2 
http://orcid.org/0000-0002-4506-7247

Marlenildo Ferreira Melo2 
http://orcid.org/0000-0001-7449-6916

1Federal University of Paraíba, Agricultural Sciences Center, Campus II, Areia, Paraíba, Brazil.

2Federal University of the Semi-Arid Region, Mossoró, Rio Grande do Norte, Brazil.

Abstract:

Background and Aims:

Determining the leaf area is essential for studies on growth, propagation, and ecophysiology of forest species. Developing quick, practical, and accurate methods is needed to estimate leaf area without destroying leaves. Therefore, this research aimed to obtain an equation from regression models that meaningfully estimate the leaf area of Erythroxylum pauferrense using linear dimensions of its leaf blades.

Methods:

For this purpose, 1200 leaves were randomly collected from different plants in the Mata do Pau-Ferro, a state park located in Areia city, Paraíba state, Brazil. Equations were fitted from simple linear, linear without intercept, quadratic, cubic, power, and exponential regression models. Next, the best equation was selected by checking the following assumptions: higher determination coefficient (R²) and Willmott's index (d), lower Akaike information criterion (AIC) and root mean square error (RMSE), as well as the BIAS index closest to zero.

Key results:

Based on the criteria used, all equations fitted using the product of length by width (L.W) can estimate the leaf area of E. pauferrense.

Conclusions:

The equation ŷ=0.6740*LW from the linear model without intercept significantly estimates the leaf area of E. pauferrense in a quick and practical way (R²=0.9960; d=0.9953; AIC=1231.61; RMSE=0.4255; BIAS=-0.0130).

Key words: allometric equations; biometry; guarda-orvalho; leaf modeling

Resumen:

Antecedentes y Objetivos:

La determinación del área foliar es esencial para los estudios sobre crecimiento, propagación y ecofisiología de especies forestales. Es necesario desarrollar métodos rápidos, prácticos y precisos para estimar el área de la hoja sin destruir las hojas. Por lo tanto, esta investigación tuvo como objetivo obtener una ecuación a partir de modelos de regresión que estimen significativamente el área foliar de Erythroxylum pauferrense, utilizando dimensiones lineales de sus láminas foliares.

Métodos:

Para este propósito, se recolectaron al azar 1200 hojas de diferentes plantas en Mata do Pau-Ferro, un parque estatal ubicado en la ciudad de Areia, estado de Paraíba, Brasil. Las ecuaciones se ajustaron a partir de modelos de regresión lineal simple, lineal sin intercepción, cuadrática, cúbica, de potencia y exponencial. Luego, se seleccionó la mejor ecuación verificando los siguientes supuestos: coeficiente de determinación más alto (R²) e índice de Willmott (d), criterio de información de Akaike más bajo (AIC) y error cuadrático medio (RMSE), así como el índice BIAS más cercano a cero.

Resultados clave:

Basado en los criterios utilizados, todas las ecuaciones ajustadas usando el producto de largo por ancho (L.W) pueden estimar el área foliar de E. pauferrense.

Conclusiones:

La ecuación ŷ=0.6740*LW del modelo lineal sin intercepción estima significativamente el área foliar de E. pauferrense de una manera rápida y práctica (R²=0.9960; d=0.9953; AIC=1231.61; RMSE=0.4255; BIAS=-0.0130).

Palabras clave: ecuaciones alométricas; biometría; guarda-orvalho; modelado de hojas

Introduction

Erythroxylum pauferrense Plowman (Erythroxylaceae) is a plant species endemic to northeastern Brazil, where it is popularly known as “Guarda-orvalho”. This species is an understory shrub, 1.5 to 4 m high, found only in Paraíba state, where its holotype originates from Areia city (Loiola et al., 2007). There are small subpopulations of this species in isolated fragments of humid forests, because its habitat has been destroyed by deforestation, reducing considerably the number of adult individuals. Therefore, E. pauferrense is listed in the “EN” category according to the Lista Vermelha da Flora do Brazil (CNCFlora, 2020), which means that it is an endangered species. Despite this, the species has high ecological importance, acting in the preservation of the endemic genetic resources of the regions of occurrence (Ribeiro et al., 2019c).

Given the importance of E. pauferrense, physiological studies on its growth, propagation, development, and reproduction become necessary. Therefore, studies for determining leaf area are relevant, since this growth variable is one of the most used to assess the ecophysiology of forest and crop species (Wang and Zhang, 2012; Santana et al., 2018). In addition, leaves gather characteristics that directly influence the interception and absorption of light for photosynthetic activity, transpiration rate, and stoma opening, thus affecting the metabolism and dry matter production (Spann and Heerema, 2010; Candido et al., 2013; Osnas et al., 2013; Schmildt et al., 2014; Taiz et al., 2017).

Leaf area can be determined by many methods, classified as direct (destructive and non-destructive) and indirect (non-destructive) (Peksen, 2007; Malagi et al., 2010; Sousa et al., 2015; Toebe et al., 2019). Direct methods are simple to perform and accurate, but laborious, in addition to becoming unviable for endangered species, plants smaller in size, and individuals at a growth stage in which it is not possible to remove leaves, because they can severely damage the plant (Mota et al., 2014; Schmildt et al., 2014). In contrast, indirect methods are quick to perform, precise for plants growing in different environmental conditions, and allow multiple evaluations in the same individual through regression equations, which is fitted using leaf blade dimensions (such as length and width), without destroying the sample (Bosco et al., 2012; Lima et al., 2012; Pompelli et al., 2012; Souza and Amaral, 2015; Ribeiro et al., 2019a).

Adjustment of regression equations to estimate leaf area has been employed for many forest species, such as Combretum leprosum Mart. (Candido et al., 2013), Acrocomia aculeata (Jacq.) Lodd. ex Mart. (Mota et al., 2014), Merremia aegyptia (L.) Urban (Assis et al., 2015), Juglans regia L. (Keramatlou et al., 2015), Handroanthus chrysotrichus (Mart. ex A. DC.) Mattos, Tabebuia impetiginosa (Mart. ex DC.) Standl., Tabebuia roseoalba (Ridl.) Sand. (Monteiro et al., 2017), Erythroxylum simonis Plowman (Ribeiro et al., 2018a), Erythroxylum citrifolium A.St.-Hil. (Ribeiro et al., 2019a), and Psychotria carthagenensis Jacq. and Psychotria hoffmannseggiana (Willd. ex Schult.) Müll. Arg. (Ribeiro et al., 2019b). For E. pauferrense, a regression model for estimating its leaf area is of fundamental importance, because it may contribute to future studies on the propagation, preservation, and conservation of this species in forest remnants of the Atlantic Forest. Therefore, this research aimed to obtain an equation from regression models that meaningfully estimate the leaf area of E. pauferrense using linear dimensions of its leaf blades.

Materials and Methods

The study was carried out in the Mata do Pau-Ferro (6°58'12''S, 35°42'15''W), a state park located in Areia city, Paraíba state, Northeast region, Brazil (Fig. 1). The conservation unit is situated in the Brejo Paraibano microregion, Agreste mesoregion, where altitudes reach 400 to 600 m, 22 °C average temperature, and 1400 mm average annual rainfall (Ribeiro et al., 2018b). Classified according to Peel et al. (2007) as Aw', the climate of the region is hot and humid tropical with autumn-winter rains.

Figure 1: Geographic location of Parque Estadual Mata do Pau-Ferro, situated in Areia city, Paraíba state, Northeast Brazil. 

For performing allometric measurements, 1200 leaves of different shapes and sizes were collected from E. pauferrense (herbarium EAN, Federal University of Paraiba, Campus II-CCA, voucher number 24843) in 50 mother plants (without damaging the plants), but choosing those healthy limbs without pest, disease and abiotic damages (Bianco et al., 2007; Lucena et al., 2011; Schmildt et al., 2014). As they were collected, the leaves were stored in thermal containers with ice to avoid water loss, and then transported to the Plant Ecology Laboratory, Federal University of Paraíba (Campus II). In the laboratory, maximum length (L) (cm) and width (W) (cm) of each leaf blade were measured using a millimetric ruler, as shown in Figure 2, and values were used to calculate the product of length by width (L.W) (cm²), length by length (L.L) (cm²), and width by width (W.W) (cm²). Moreover, to determine the real leaf area (LA) (cm²), each limb was photocopied using a scanner (Epson, model L395, Tokyo, Japan), and the images were processed and analyzed in ImageJ® (Powerful Image Analysis) software (Ribeiro et al., 2018a).

Figure 2: Linear dimensions (maximum length (L) and maximum width (W)) of leaf blade Erythroxylum pauferrense Plowman used to estimate leaf area. 

A descriptive analysis was performed for L, W, L.W, L.L, W.W, and LA of all 1200 leaf blades, obtaining the minimum, maximum and average values, mean, total amplitude, median, variance, standard deviation, standard error, coefficient of variation, asymmetry, and kurtosis. Also, the data were analyzed for normality using the Lilliefors test.

Allometric equations were obtained by simple linear, linear without intercept, quadratic, cubic, power, and exponential regression models, as described in Table 1. Then, the equation that meaningfully estimated the leaf area of E. pauferrense based on linear dimensions of its leaf blade was selected by checking the following assumptions: higher determination coefficient (R²) and Willmott's index (d) (Willmott et al., 1981) (equation 1); lower Akaike information criterion (AIC) (Akaike, 1974) (equation 2) and root mean square error (RMSE) (Janssen and Heuberger, 1995) (equation 3); and the BIAS index closest to zero (Leite and Andrade, 2002) (equation 4). Statistical analyses were performed using the R package 'hydroGOF' (Zambrano-Bigiarini, 2020) in R software v.4.0.0 (R Core Team, 2020).

Table 1: Description of the regression models used to estimate the leaf area of Erythroxylum pauferrense Plowman. 

Model Description (Equation)
Simple linear LA=a+b*L
Simple linear LA=a+b*W
Simple linear LA=a+b*(L.W)
Linear without intercept LA=b*(L.W)
Simple linear LA=a+b*(L.L)
Simple linear LA=a+b*(W.W)
Quadratic LA=a*L 2 +b*L+c
Quadratic LA=a*W 2 +b*W+c
Quadratic LA=a*(L.W) 2 +b*(L.W)+c
Quadratic LA=a*(L.L) 2 +b*(L.L)+c
Quadratic LA=a*(W.W) 2 +b*(W.W)+c
Cubic LA=a*L 3 +b*L 2 +L*C+d
Cubic LA=a*W 3 +b*W 2 +C*W+d
Cubic LA=a*(L.W) 3 +b*(L.W) 2 +C*(L.W)+d
Cubic LA=a*(L.L) 3 +b*(L.L) 2 +C*(L.L)+d
Cubic LA=a*(W.W) 3 +b*(W.W) 2 +C*(W.W)+d
Power LA=a*Lb
Power LA=a*Wb
Power LA=a*(L.W)b
Power LA=a*(L.L)b
Power LA=a*(W.W)b
Exponential LA=a*bL
Exponential LA=a*bW
Exponential LA=a*b(L.W)
Exponential LA=a*b(L.L)
Exponential LA=a*b(W.W)

d=1-∑i = 1 n(y^ᵢ - yᵢ)²∑i = 1 n(y^ ´ᵢ + |y ´ᵢ|)² equation 1:

AIC=- 2ln Lx\θ^+2p equation 2:

RMSE=∑i=1n(y^i-yi)²n equation 3:

BIAS= ∑i=1n(y^i-yi)∑i=1n(yi)equation 4:

where: y^ᵢis the estimated leaf area values; yᵢ is the observed leaf area values; y-ᵢ is the mean of observed values; y^ ´ᵢ=y^ᵢ-y-; y ´ᵢ=yᵢ-y-; Lx\θ^ is the maximum likelihood function, defined as the product of density function; p is the number of model parameters; n is the number of observations.

Results

The leaf blades of E. pauferrense showed length (L) that ranged from 0.924 to 6.991 cm, with 3.925 cm on average and 6.067 cm amplitude, while width (W) ranged from 0.569 to 3.658 cm, with 2.130 on average and 3.089 cm amplitude. In turn, the product of length by width (L.W) varied from 0.773 to 25.397 cm², with 8.971 cm² on average and 24.624 cm² amplitude; product of length by length (L.L) differed between 1.848 and 13.982 cm², with 7.852 cm² on average and 12.134 cm² amplitude; and product of width by width (W.W) expressed values from 0.323 to 13.381 cm², 4.873 cm² on average and 13.057 cm² amplitude. Finally, leaf area (LA) ranged from 0.475 to 18.075 cm², 6.033 cm² on average, and 17.600 cm² amplitude (Table 2). Regarding variation in data, the lowest coefficients of variation were those from length and width (30.08 and 27.19%, respectively), whereas the highest coefficients were those from L.W (50.75%), L.L (45.03%), W.W (49.55%), and LA (51.78%) (Table 2).

Table 2: Minimum, maximum, mean, total amplitude, median, variance, standard deviation, standard error, coefficient of variation (CV), asymmetry, kurtosis, and Lilliefors test for normality of length (L), width (W), product of length by width (L.W), product of length by length (L.L), product of width by width (W.W), and leaf area (LA) of 1200 leaf blades of Erythroxylum pauferrense Plowman. a Asymmetry differs from zero by the t-test at 5% probability; b Kurtosis differs from three by the t-test at 5% probability; *Significant at 5% probability; ** Significant at 1% probability. 

Descriptive statistic L (cm) W (cm) L.W (cm²) L.L (cm²) W.W (cm²) LA (cm²)
Minimum 0.924 0.569 0.773 1.848 0.323 0.475
Maximum 6.991 3.658 25.397 13.982 13.381 18.075
Mean 3.925 2.130 8.971 7.852 4.873 6.033
Total amplitude 6.067 3.089 24.624 12.134 13.057 17.600
Median 3.931 2.165 8.472 7.862 4.687 5.641
Variance 1.394 0.335 20.728 1.054 1.188 9.760
Standard deviation 1.180 0.579 4.552 2.358 2.414 3.124
Standard error 0.035 0.017 0.138 0.071 0.073 0.094
CV (%) 30.08 27.19 50.75 45.03 49.55 51.78
Asymmetrya -0.154 -0.277 0.435 -0.152 0.4128 0.512
Kurtosis + 3b 2.738 2.769 2.838 2.739 2.823 2.974
Lilliefors 0.0017** 0.0158* <0.0001** 0.0018** <0.0001** <0.0001**

Scatterplots between pairs of the variables L, W, L.W, L.L, W.W, and LA evidenced different relationships between them, suggesting adjustments of linear and non-linear models (Fig. 3).

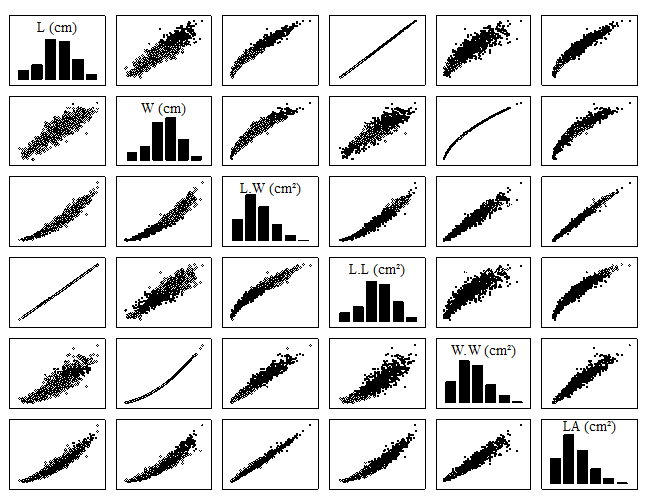
Figure 3: Histograms and scatterplots between length (L), width (W), product of length by width (L.W), product of length by length (L.L), product of width by width (W.W), and leaf area (LA) of Erythroxylum pauferrense Plowman. 

Distribution of the 1200 leaf blades of E. pauferrense relative to different size classes is shown in Fig. 4. It was found that 58.6% of leaf areas were between 0.45 and 6 cm², indicating that most leaves from this forest species are small in size (Fig. 4).

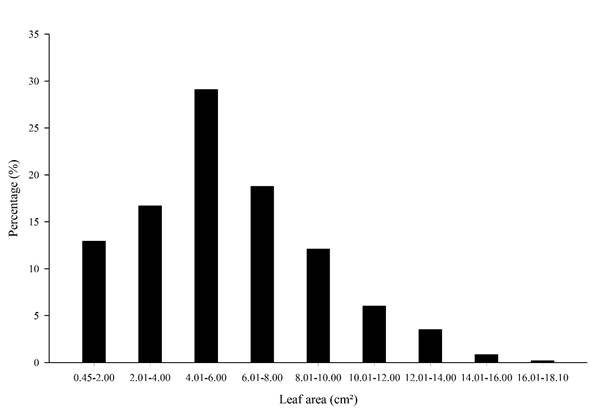
Figure 4: Percentage distribution of leaf area (LA) of 1200 leaf blades of Erythroxylum pauferrense Plowman by different size classes. 

The regression models and adjusted allometric equations for estimating the leaf area (ŷ) as a function of linear dimensions of the leaf blades (L, W, L.W, L.L, and W.W) are shown in Table 3. Among the adjusted equations, the linear regression model without intercept (when the regression line does not pass through the origin) using the product of length by width (L.W) showed the highest R² (0.9960) and d (0.9953), lowest RMSE (0.4255) and AIC (1231.61), and BIAS index closest to zero (-0.0130) (Table 3). Therefore, ŷ=0.6740*L.W was the equation that best estimated the leaf area of E. pauferrense through the linear dimensions of its leaf blades. Moreover, this equation predicts that 67.40% variation in leaf area can be explained by the product of length by width (L.W).

Table 3: Regression models, equations, determination coefficient (R²), Akaike information criterion (AIC), root mean square error (RMSE), Willmott's index (d), and BIAS index for linear dimensions of leaf blades of Erythroxylum pauferrense Plowman. (1) Linear dimensions: length (L) and width (W). 

Model x1 Equation R² AIC RMSE d BIAS
Linear L ŷ=-3.814+2.509*L 0.8987 3064.66 0.9932 0.9727 -0.0377
Linear W ŷ=-4.759+5.066*W 0.8821 3229.62 1.0718 0.9678 -0.0495
Linear L.W ŷ=-0.0636+0.6796*LW 0.9810 1250.10 0.4297 0.9951 -0.0296
Linear (0.0) L.W ŷ=0.6740*LW 0.9960 1231.61 0.4255 0.9953 -0.0130
Linear L.L ŷ=-3.842+1.257*LL 0.9007 3043.84 0.9837 0.9733 -0.0389
Linear W.W ŷ=0.01467+1.23495*WW 0.9106 2929.61 0.9332 0.9761 -0.0365
Quadratic L ŷ=-0.3010+0.4832*L+0.2641*L² 0.9224 2777.17 0.8690 0.9795 0.0330
Quadratic W ŷ=-0.1158+0.1364*W+1.2023*W² 0.9102 2936.22 0.9352 0.9760 0.0396
Quadratic L.W ŷ=0.1081+0.6355*LW+0.0022*LW² 0.9814 1232.82 0.4257 0.9951 0.0230
Quadratic L.L ŷ=-0.3702+0.2578*LL+0.0651*LL² 0.9237 2760.23 0.8622 0.9799 -0.0362
Quadratic W.W ŷ=-0.0910+1.2847*WW-0.0046*WW² 0.9107 2930.11 0.9325 0.9762 -0.0365
Cubic L ŷ=-0.1475+0.3358*L+0.3058*L²-0.0036*L³ 0.9224 2779.04 0.8689 0.9795 0.0313
Cubic W ŷ=1.0122-1.8363*W+2.2417*W²-0.1693*W³ 0.9104 2934.65 0.9336 0.9761 0.0331
Cubic L.W ŷ=0.0655+0.6551*LW-0.000012*LW²+0.00007*LW³ 0.9814 1252.96 0.4307 0.9951 0.0239
Cubic L.L ŷ=-0.2870+0.2179*LL+0.070*LL²-0.00024*LL³ 0.9236 2762.19 0.8622 0.9799 -0.0356
Cubic W.W ŷ=0.2031+1.0397*WW+0.0468*WW²-0.0030*WW³ 0.9111 2925.51 0.9297 0.9763 -0.0358
Potency L ŷ=0.4939*L1.7847 0.9226 2775.08 0.8689 0.9795 0.0319
Potency W ŷ=1.252*W1.988 0.9103 2934.26 0.9352 0.9760 -0.0276
Potency L.W ŷ=0.6422*LW1.0193 0.9812 1240.80 0.4279 0.9951 0.0230
Potency L.L ŷ=0.1429*LL1.7860 0.9237 2758.26 0.8622 0.9798 -0.0304
Potency W.W ŷ=1.2508*WW0.9943 0.9107 2929.40 0.9331 0.9761 -0.0397
Exponential L ŷ=1.159*1.485L 0.9033 3036.43 0.9803 0.9724 -0.0566
Exponential W ŷ=0.9401*2.2839W 0.8923 3149.88 1.0331 0.9691 -0.0555
Exponential L.W ŷ=2.503*1.094LW 0.8923 2864.81 1.0331 0.9691 -0.0555
Exponential L.L ŷ=1.157*1.219LL 0.9039 3029.25 0.9771 0.9726 -0.0573
Exponential W.W ŷ=2.552*1.177WW 0.8426 3574.95 1.2571 0.9511 -0.0852

Data fit a normal distribution, and variances were homoscedastic, supporting that the equation ŷ=0.6740*L.W can meaningfully estimate the leaf area of E. pauferrense (Fig. 5). Moreover, the estimated leaf area using this equation positively correlated with the real leaf area, with a 0.9819 determination coefficient (R²) (Fig. 6).

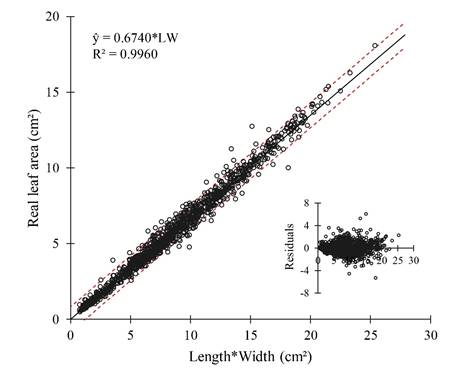
Figure 5: Relationship between the real leaf area (LA) and the product of length (L) by width (W) of leaf blades of Erythroxylum pauferrense Plowman, using the equation ŷ = 0.6740*LW. Residual dispersion pattern for this model is shown in the inserted chart. 

Figure 6: Relationship between the real leaf area and leaf area of Erythroxylum pauferrense Plowman estimated by the equation ŷ=0.6740*LW. Residual dispersion pattern for this model is shown in the inserted chart . 

Discussion

High values of amplitude, standard deviation, standard error and coefficient of variation found in this study are of fundamental importance in studies that estimate the leaf area using regression models (Levine et al., 2017; Oliveira et al., 2019a). Such great variation in the data indicates the reliability of models, which can represent large, medium, and small leaves, allowing measurements at different phenological stages of the plant (Pezzini et al., 2018). Thus, the number of leaves used in this study (1200) was adequate for estimating the leaf area of the species through linear dimensions. Moreover, high variation in L.W and LA values was also observed in previous studies (Schmildt et al., 2015, 2016; Leite et al., 2017; Ribeiro et al., 2018a, 2019b).

The coefficient of kurtosis (k) value less than 3 (k<3) is an indicative that all analyzed variables had a platykurtic distribution, expected for a normal distribution. This behavior shows that the frequency distribution function of the variables is more flattened than the normal distribution (Ribeiro et al., 2020). This distance from a normal distribution observed in all variables (L, W, L.W, L.L, W.W, and LA) occurred due to deviations in the coefficients of asymmetry and kurtosis. This behavior was also observed in previous studies with other plant species (Cargnelutti Filho et al., 2015; Carvalho et al., 2017a; Ribeiro et al., 2019a; Toebe et al., 2019).

Most leaves from this forest species are small in size. In other species from the Erythroxylaceae family, Ribeiro et al. (2018a, 2019a) reported similar results.

The determination coefficients (R²) were greater than 0.84, indicating that at least 84% variation in leaf area of E. pauferrense can be explained by the proposed equations. Also, the equations adjusted using the product of length by width (L.W) met the assumptions for estimating leaf area, thus best fitting the regression models (Carvalho et al., 2017b; Pezzini et al., 2018; Guimarães et al., 2019; Oliveira et al., 2019b), except for the exponential model, where best indexes were obtained using the product of length by length (L.L).

This same regression model was recommended to estimate the leaf area of other forest species, such as Combretum leprosum (LA=0.7103*L.W; Candido et al., 2013), Crotalaria juncea L. (LA=0.7390*L.W; Carvalho et al., 2017a), Tectona grandis L. f. (LA=0.4449*L.W; Braga et al., 2018), and Ceiba glaziovii (Kuntze) K. Schum. (LA=0.4549*L.W; Ribeiro et al., 2020).

According to the proposed equation for estimating the leaf area, data showed low dispersion from the regression line in the scatterplot, indicating that variation was constant, and residuals were normally distributed. The equation proposed here may contribute to ecological studies on growth, development, and propagation of E. pauferrense, acting in the preservation of this endangered species in forest remnants.

Leaf area of E. pauferrense can be precisely estimated through a non-destructive method using linear dimensions of its leaf blades. Equations that use the product of length by width (L.W) can meaningfully estimate the leaf area of E. pauferrense. The equation ŷ=0.6740*LW from the linear model without intercept significantly estimates the leaf area of E. pauferrense in a quick and practical way.

Acknowledgements

We are grateful to the journal reviewers and editors for their suggestions for improving the manuscript and to the Center of Agrarian Sciences, Federal University of Paraíba, for the support.

Literature cited

Akaike, H. 1974. A new look at the statistical model identification. IEEE Transactions on Automatic Control 19(6): 716-723. DOI: https://doi.org/10.1109/tac.1974.1100705 [ Links ]

Assis, J. P., P. C. F. Linhares, R. P. Souza, M. F. S. Pereira and A. M. B. Almeida. 2015. Estimação da área foliar da “jitirana” (Merremia aegyptia (L.) Urban), através de modelos de regressão para Mossoró - RN. Revista Verde de Agroecologia e Desenvolvimento Sustentável 10(4): 75-81. DOI: https://doi.org/10.18378/rvads.v10i4.3872 [ Links ]

Bianco, S., M. S. Bianco, M. C. M. D. Pavani and D. J. Duarte. 2007. Estimativa da área foliar de Ipomoea hederifolia e Ipomoea nil Roth: usando dimensões lineares do limbo foliar. Planta Daninha 25(2): 325-329. DOI: https://doi.org/10.1590/S0100-83582007000200012 [ Links ]

Bosco, L. C., H. Bergamaschi, L. S. Cardoso, V. A. de Paula and B. Casamali. 2012. Seleção de modelos de regressão para estimar a área foliar de macieiras 'Roayal Gala' e 'Fuji Suprema' sob tela antigranizo e em céu aberto. Revista Brasileira de Fruticultura 34(2): 504-514. DOI: https://doi.org/10.1590/S0100-29452012000200024 [ Links ]

Braga, N. S., A. C. A. Araujo, I. D. A. Araujo, A. A. S. Souza, D. S. Cunha, V. J. G. Gil, I. S. Rocha, J. V. S. Almeida and J. T. L. Silva. 2018. Modelos matemáticos para estimativa de área foliar de teca (Tectona grandis L. f.). Nucleus 15(2): 331-339. DOI: http://doi.org/10.3738/1982.2278.2910 [ Links ]

Candido, W. S., M. F. B. Coelho, S. S. S. Maia, C. S. M. C. Cunha and R. C. P. Silva. 2013. Modelo para estimar a área foliar de Combretum leprosum Mart. Acta Agronômica 62(1): 37-41. [ Links ]

Cargnelutti Filho, A., M. Toebe, B. M. Alves, C. Burin and J. A. Kleinpaul. 2015. Estimação da área foliar de canola por dimensões foliares. Bragantia 74(2): 139-148. DOI: https://doi.org/10.1590/1678-4499.0388 [ Links ]

Carvalho, J. O., M. Toebe , F. L. Tartaglia, C. T. Bandeira and A. L. Tambara. 2017a. Leaf area estimation from linear measurements in different ages of Crotalaria juncea plants. Anais da Academia Brasileira de Ciências 89(3): 1851-1868. DOI: https://doi.org/10.1590/0001-3765201720170077 [ Links ]

Carvalho, L. B., E. A. Alves and S. Bianco. 2017b. Non-destructive model to predict Commelina diffusa leaf area. Planta Daninha 35: 1-5. DOI: https://doi.org/10.1590/s0100-83582017350100088 [ Links ]

CNCFlora. 2020. Erythroxylum pauferrense. Lista Vermelha da flora brasileira versão 2012.2 Centro Nacional de Conservação da Flora. Rio de Janeiro, Brazil. http://cncflora.jbrj.gov.br/portal/pt-br/profile/Erythroxylumpauferrense (consulted March, 2020). [ Links ]

Guimarães, M. J. M., M. A. C. Filho , F. A. Gomes Junior, M. A. M. Silva, C. V. O. Alves and I. Lopes. 2019. Modelos matemáticos para a estimativa da área foliar de mandioca. Revista de Ciências Agrárias 62: 1-5. DOI: http://dx.doi.org/10.22491/rca.2019.3015 [ Links ]

Janssen, P. H. M. and P. S. C. Heuberger. 1995. Calibration of process-oriented models. Ecological Modelling 83(1-2): 55-66. DOI: https://doi.org/10.1016/0304-3800(95)00084-9 [ Links ]

Keramatlou, I., M. Sharifani, H. Sabouri, M. Alizadeha and B. Kamkar. 2015. A simple linear model for leaf area estimation in Persian walnut (Juglans regia L.). Scientia Horticulturae 184(1): 36-39. DOI: https://doi.org/10.1016/j.scienta.2014.12.017 [ Links ]

Leite, H. G. and V. C. L. Andrade. 2002. Um método para condução de inventários florestais sem o uso de equações volumétricas. Revista Árvore 26(3): 321-328. DOI: https://doi.org/10.1590/S0100-67622002000300007 [ Links ]

Leite, M. L. M. V., L. R. R. Lucena, E. H. Sá Júnior and M. G. Cruz. 2017. Estimativa da área foliar em Urochloa mosambicensis por dimensões lineares. Revista Agropecuária Técnica 38(1): 9-16. DOI: https://doi.org/10.25066/agrotec.v38i1.32041 [ Links ]

Levine, D. M., D. F. Stephan and K. A. Szabat. 2017. Statistics for managers using Microsoft Excel. Global edition Person. London, UK. 728 pp. [ Links ]

Lima, R. T., P. J. O. P. Souza, J. C. Rodrigues and M. J. A. Lima. 2012. Modelos para estimativa da área foliar da mangueira utilizando medidas lineares. Revista Brasileira de Fruticultura 34(4): 974-980. DOI: https://doi.org/10.1590/S0100-29452012000400003 [ Links ]

Loiola, M. I. B., M. F. Agra, G. S. Baracho and R. T. Queiroz. 2007. Flora da Paraíba, Brasil: Erythroxylaceae Kunth. Acta Botanica Brasilica 21(2): 473-487. DOI: https://doi.org/10.1590/S0102-33062007000200020 [ Links ]

Lucena, R. R. M., T. M. V. Batista, J. L. D. Dombroski, W. A. R. Lopes and G. S. O. Rodrigues. 2011. Medição de área foliar de aceroleira. Revista Caatinga 24(2): 40-45. [ Links ]

Malagi, G., I. Citadin, S. Scariot and L. Reis. 2010. Método não destrutivo para determinação da área foliar da videira, cultivar BRS-Violeta. Revista Brasileira de Fruticultura 32(4): 1250-1254. DOI: https://doi.org/10.1590/S0100-29452011005000005 [ Links ]

Monteiro, E. B., A. C. Silva, A. P. Souza, C. C. Silva, V. S. Kazama and A. A. Tanaka. 2017. Statistical parameters to estimate the leaf area of native forest seedlings of genus Tabebuia and Handroanthus. Bioscience Journal 33(4): 956-967. DOI: https://doi.org/10.14393/BJ-v33n4a2017-33977 [ Links ]

Mota, C. S., H. G. Leite and M. A. O. Cano. 2014. Equações para estimar área foliar de folíolos de Acrocomia aculeta. Pesquisa Florestal Brasileira 34(79): 217-224. DOI: https://doi.org/10.4336/2014.pfb.34.79.684 [ Links ]

Oliveira, V. S., J. K. B. Galote, I. V. Damaceno, N. S. Furtado, K. T. H. Santos, J. S. H. Santos, G. P. Santos, H. Chisté, O. Schmildt, M. P. Czepak, S. D. Arantes, E. L. Vitória and E. R. Schmildt. 2019a. Estimation of single leaf area of Acacia mangium Willd. International Journal of Plant & Soil Science 28(3): 1-7. DOI: https://doi.org/10.9734/ijpss/2019/v28i330107 [ Links ]

Oliveira, V. S. , L. R. Hell, K. T. H. Santos , H. R. Pelegrini, J. S. H. Santos , G. E. Oliveira, A. L. Nascimento, G. P. Santos , O. Schmildt , M. P. Czepak , S. D. Arantes , R. S. Alexandre andE. R. Schmildt . 2019b. Estimation of leaf area of jackfruit through non-destructive method. Journal of Agricultural Science 11(6): 77-85. DOI: https://doi.org/10.5539/jas.v11n6p77 [ Links ]

Osnas, J. L. D., J. W. Lichstein, P. B. Reich and S. W. Pacala. 2013. Global leaf trait relationships: mass, area, and the leaf economics spectrum. Science 340(6133): 741-744. DOI: https://doi.org/10.1126/science.1231574 [ Links ]

Peel, M. C., B. L. Finlayson and T. A. McMahon. 2007. Updated world map of the Köppen-Geiger climate classification. Hydrology and Earth System Sciences 11: 1633-1644. DOI: https://doi.org/10.5194/hess-11-1633-2007 [ Links ]

Peksen, E. 2007. Non-destructive leaf area estimation model for faba bean (Vicia faba L.). Scientia Horticulturae 113(4): 322-328. DOI: https://doi.org/10.1016/j.scienta.2007.04.003 [ Links ]

Pezzini, R. V., A. Cargnelutti Filho, B. M. Alves , D. N. Follmann, J. A. Leinpaul, C. A. Wartha and D. L. Silveira. 2018. Models for leaf area estimation in dwarf pigeon pea by leaf dimensions. Bragantia 77(2): 221-229. DOI: https://doi.org/10.1590/1678-4499.2017106 [ Links ]

Pompelli, M. F., W. C. Antunes, D. T. R. G. Ferreira, P. G. S. Cavalcante, H. C. L. Wanderley Filho and L. Endres. 2012. Allometric models for non-destructive leaf area estimation of Jatropha curcas. Biomass and Bioenergy 36: 77-85. DOI: https://doi.org/10.1016/j.biombioe.2011.10.010 [ Links ]

R Core Team. 2020. R: A language and environment for statistical computing http://www.R-project.org/.R Foundation for Statistical Computing. Vienna, Austria. [ Links ]

Ribeiro, J. E. S., A. J. S. Barbosa and M. B. Albuquerque. 2018a. Leaf Area Estimate of Erythroxylum simonis Plowman by Linear Dimensions. Floresta e Ambiente 25(2): 1-7. DOI: https://doi.org/10.1590/2179-8087.010817 [ Links ]

Ribeiro, J. E. S. , A. J. S. Barbosa , S. F. Lopes, W. E. Pereira andM. B. Albuquerque . 2018b. Seasonal variation in gas exchange by plants of Erythroxylum simonis Plowman. Acta Botanica Brasilica 32(2): 287-296. DOI: https://doi.org/10.1590/0102-33062017abb0240 [ Links ]

Ribeiro, J. E. S. , E. S. Coêlho, F. R. A. Figueiredo, S. F. Lopes andM. B. Albuquerque . 2019a. Estimation of leaf area of Erythroxylum citrifolium from linear leaf dimensions. Bioscience Journal 35(6): 1923-1931. DOI: https://doi.org/10.14393/BJ-v35n6a2019-41743 [ Links ]

Ribeiro, J. E. S. , E. S. Coêlho , F. R. A. Figueiredo , W. E. Pereira andM. B. Albuquerque . 2019b. Leaf area estimation for Psychotria carthagenensis and Psychotria hoffmannseggiana as a function of linear leaf dimensions. Acta Scientiarum-Biological Sciences 41: 1-8. DOI: https://doi.org/10.4025/actascibiolsci.v41i1.43494 [ Links ]

Ribeiro, J. E. S. , F. R. A. Figueiredo , E. S. Coêlho , W. E. Pereira andM. B. Albuquerque . 2020. A non-destructive method for estimating leaf area of Ceiba glaziovii (Kuntze) K. Schum. Floresta 50(1): 1063-1070. DOI: http://dx.doi.org/10.5380/rf.v50i1.61088 [ Links ]

Ribeiro, J. E. S. , A. P. Leite, J. S. Nóbrega, E. U. Alves, R. L. A. Bruno andM. B. Albuquerque . 2019c. Temperatures and substrates for germination and vigor of Erythroxylum pauferrense Plowman seeds. Acta Scientiarum-Biological Sciences 41(1): 1-7. DOI: https://doi.org/10.4025/actascibiolsci.v41i1.46030 [ Links ]

Santana, H. A., B. R. Rezende, W. Santos and A. R. Silva. 2018. Modelos para predição da área foliar individual de leguminosas forrageiras. Revista Ceres 65(2): 204-209. DOI: https://doi.org/10.1590/0034-737x201865020013 [ Links ]

Schmildt, E. R., J. J. Hueso and J. Cuevas. 2014. Allometric models for determining leaf area of vine ‘Sugraone’. Ciência e Técnica Vitivinícola 29(10): 61-81. DOI: https://doi.org/10.17660/th2017/72.1.2 [ Links ]

Schmildt, E. R. , J. A. T. Amaral, J. S. Santos andO. Schmildt . 2015. Allometric model for estimating leaf area in clonal varieties of coffee (Coffea canephora). Revista Ciência Agronômica 46(4): 740-748. DOI: https://doi.org/10.5935/1806-6690.20150061 [ Links ]

Schmildt, E. R. , L. S. Oliari, O. Schmildt , R. S. Alexandre , J. A. Brumatti and D. G. Viana. 2016. Determinação da área foliar de macadâmia a partir de dimensões lineares do limbo foliar. Revista Agro@mbiente 10(3): 209-216. DOI: http://doi.org/10.18227/1982-8470ragro.v10i3.3332 [ Links ]

Sousa, L. F., J. G. D. Santos, E. Alexandrino, R. M. Maurício, A. D. Martins and J. T. L. Sousa. 2015. Método prático e eficiente para estimar a área foliar de gramíneas forrageiras tropicais. Archivos de Zootecnia 64(245): 83-85. DOI: https://doi.org/10.21071/az.v64i245.380 [ Links ]

Souza, M. C. and C. L. Amaral. 2015. Non-destructive linear model for leaf area estimation in Vernonia ferruginea Less. Brazilian Journal of Biology 75(1): 152-156. DOI: https://doi.org/10.1590/1519-6984.09813 [ Links ]

Spann, T. M. and R. J. Heerema. 2010. A simple method for nondestructive estimation of total shoot leaf area in tree fruit crops. Scientia Horticulturae 125(3): 528-533. DOI: https://doi.org/10.1016/j.scienta.2010.04.033 [ Links ]

Taiz, L., E. Zeiger, I. M. Møller and A. Murphy. 2017. Fisiologia e desenvolvimento vegetal. Artmed. Porto Alegre, Brasil. 888 pp. [ Links ]

Toebe, M., P. J. Melo, R. R. Souza, A. C. Mello and F. L. Tartaglia. 2019. Leaf area estimation in triticale by leaf dimensions. Revista Brasileira de Ciências Agrárias 14(2): 1-9. DOI: https://doi.org/10.5039/agraria.v14i2a5656 [ Links ]

Wang, Z. and L. Zhang. 2012. Leaf shape alters the coefficients of leaf area estimation models for Saussurea stoliczkai in central Tibet. Photosynthetica 50(3): 337-342. DOI: https://doi.org/10.1007/s11099-012-0039-1 [ Links ]

Willmott, C. J. 1981. On the validation of models. Physical Geography 2(2): 184-194. DOI: https://doi.org/10.1080/02723646.1981.10642213 [ Links ]

Zambrano-Bigiarini, M. 2020. HydroGOF: Goodness-of-fit functions for comparison of simulated and observed hydrological time series. R package version 3.6.3. DOI: https://doi.org/10.5281/zenodo.839854 [ Links ]

Author contributions:

JESR, ESC and FRAF collected the data, carried out biometric evaluation of leaves, performed the statistical analyses, and wrote the manuscript. JESR and MFM aided in carrying out the experiment, evaluating data, and proofreading the manuscript.

Funding:

This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior-Brasil (CAPES)-Finance Code 001.

Received: April 20, 2020; Revised: May 18, 2020; Accepted: June 01, 2020; Published: June 05, 2020

3Author for correspondence: j.everthon@hotmail.com

Creative Commons License This is an open-access article distributed under the terms of the Creative Commons Attribution License

 
Av. Lázaro Cárdenas 3052, Pátzcuaro, Michoacán, MX, 61600, (52-434) 1179513