Introducción
La interpretación de los resultados experimentales es una de las etapas más importantes de cualquier trabajo científico. El científico debe habituarse a llevar a cabo representaciones gráficas de los datos obtenidos en el laboratorio para identificar tendencias y visualizar relaciones que le permitan proponer teorías o modelos, obteniendo relaciones matemáticas entre las variables dependientes, objeto de la medida, y las independientes, controladas en el experimento (Gil, 2012). Para cualquier ajuste, el objetivo es establecer una relación entre variables dependientes e independientes calculando una serie de coeficientes que pueden obtenerse mediante la aplicación del método de mínimos cuadrados. En el supuesto de una variable dependiente (y ) homocedástica y normalmente distribuida en cada nivel de la variable independiente (x ), el método de mínimos cuadrados consiste en obtener los coeficientes de la función elegida de manera que minimicen la suma de cuadrados de residuales:
siendo y i el valor real de la variable dependiente e ŷ i el valor estimado por la función ajustada para cada valor de la variable independiente x i .
Este método resulta sencillo cuando se trabaja con relaciones lineales entre 2 variables (Harvey, 2000; Miller y Miller, 2002). Las matemáticas asociadas a ajustes no lineales pueden resultar algo más complejas, dependiendo del nivel de conocimiento del usuario (De Levie, 2000). En algunas ocasiones se trabaja directamente con funciones no lineales, y en otras se tratan de "linealizar" mediante transformaciones adecuadas para que su tratamiento matemático sea más sencillo (Asuero y Bueno, 2011). En cualquier caso, no solo es importante calcular los coeficientes de ajuste, sino que puede ser útil y necesario obtener su error asociado, mediante el empleo de macros (Billo, 2007, De Levie, 1999), procedimientos de remuestreo (Harris, 1998) u hojas de cálculo (Moreira, Martins y Elvas-Leitão, 2006).
Los planes de estudio de química de numerosas universidades a nivel mundial incluyen asignaturas de informática y computación. El manejo de herramientas informáticas en el ámbito científico es una competencia transversal básica y su desarrollo es preponderante para los futuros químicos. Por ejemplo, estas herramientas de ajuste tienen aplicación directa en el desarrollo de competencias relacionadas con el análisis de resultados experimentales. A nivel europeo, esto se recoge en las recomendaciones de las distintas agencias de evaluación de la calidad de la enseñanza, indicando que el título debe proporcionar conocimientos adicionales en física, matemáticas e informática (ANECA, 2004). Existen diversos programas de cálculo y paquetes estadísticos que incluyen herramientas de regresión, pero uno de los de uso más extendido es quizá Microsoft Excel. Desde un punto de vista académico y profesional, parece razonable revisar las capacidades de dicho programa en la resolución de problemas de regresión, siendo este el objetivo del presente tutorial.
Metodología y datos
En este tutorial se revisan las distintas opciones de cálculo de regresión que ofrece Excel para la obtención de la ecuación de ajuste mediante gráficas, la herramienta de regresión del menú análisis de datos, funciones del programa como estimación lineal o logarítmica y la herramienta Solver. Además, se indicará la forma de obtener los errores de los parámetros estimados para este último método. El tutorial se desarrolla a partir de los ejemplos propuestos en la tabla 1:
Tabla 1 Ejemplos numéricos empleados en los distintos ajustes
| Ejemplo | Variable | Datos |
|---|---|---|
| 1 | Concentración, C (μg l−1) | 2.5, 5, 7.5, 10 |
| Absorbancia, A | 0.03, 0.06, 0.086, 0.114 | |
| 2 | Espesor, δ (μm) | 0.2, 0.5, 1.0, 2.0, 3.5, 5.0, 6.5, 8.5 |
| Intensidad, I (cuentas s−1) | 155, 133, 109, 78, 49, 30, 18, 9 | |
| 3 | Concentración, C (ng l−1) | 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 |
| Intensidad, I (u.r.l.) | 2.1, 5, 9, 12.6, 17.3, 21, 24.7, 28.4, 31, 32.9, 33.9 | |
| 4 | Concentración, [S] (mmol m−3) | 3.568, 7.213, 10.87, 14.44, 18.18, 21.93, 29.24, 36.65, 55.33, 109.8 |
| Velocidad, V (nmol m−2 s−1) | 1.42, 2.51, 3.51, 4.78, 5.4, 6.14, 7.72, 8.65, 9.96, 13.28 |
u.r.l.: unidades relativas de luminiscencia.
Ejemplo 1. Calibración con patrones para la determinación directa de cobre en aguardientes de anís mediante espectroscopia de absorción atómica con atomización electrotérmica (Jurado, Martín, Pablos, Moreda y Bermejo, 2007). Estos datos se emplearán para revisar los procedimientos de ajuste mediante la macros de regresión lineal de Excel y la función ESTIMACION.LINEAL.
Ejemplo 2. Datos de intensidad de fluorescencia de rayos X para la línea Kα del hierro en muestras de acero recubiertas con distintos espesores de estaño (Whiston, 1996). Estos datos se pueden ajustar según la ecuación 2 y se usarán para revisar la función ESTIMACION.LOGARITMICA y el ajuste definido por el usuario empleando Solver.
Ejemplo 3. Curva de calibración de fluoresceína medida mediante espectrofluorimetría (Stone y Ellis, 2011). Estos datos se ajustan a funciones del tipo de la ecuación 3, siendo necesario el uso de Solver. Por otro lado, la exponencial de base 10 se puede transformar en una exponencial de base e que a su vez puede desarrollarse como una serie de McLaurin (Skoog y Leary, 1994) y obtenerse la ecuación 4. Para valores pequeños de x se puede truncar la serie en el término cuadrático y ajustarse los datos a un polinomio de segundo grado. Este supuesto será resuelto mediante la función ESTIMACION.LINEAL.
Ejemplo 4. Flujo de captación (V) de un nutriente por un alga en función de la concentración de sustrato [S] (Ritchie y Prvan, 1996). Estos datos se ajustan a la ecuación característica de una cinética de tipo Michaelis-Menten (ecuación 5), y es necesario el uso de Solver.
Todos los ajustes realizados mediante la herramienta Solver se comprobarán resolviéndolos con el paquete estadístico Statistica 8.0 (StatSoft, Tulsa, EE.UU.).
Resultados
Procedimiento gráfico
El procedimiento gráfico de Excel permite realizar la representación de los datos y, en algunos casos, ajustar un modelo matemático de forma rápida. Para su uso, simplemente hay que disponer los datos en la hoja de cálculo, obtener un gráfico de dispersión y, colocando el puntero sobre uno de los puntos, pulsar el botón derecho y seleccionar Agregar línea de tendencia . De este modo se puede seleccionar entre varios tipos de funciones: exponencial, lineal, logarítmica, polinómica, potencial y de media móvil. Además permite hacer extrapolaciones, forzar el paso por un valor de y para x = 0 y presentar en el gráfico la ecuación de ajuste y el coeficiente de determinación r2 . Dicho coeficiente (ecuación 6) es una medida de la bondad del ajuste, donde un valor próximo a la unidad implica un mejor ajuste de los datos al modelo matemático propuesto.
En la figura 1 se representan los datos de los ejemplos propuestos, las ecuaciones ajustadas y el valor de r2 . La ecuación que propone Excel se escribe siempre de forma general, siendo x la variable independiente e y la dependiente. En la figura 1 A se observa un buen ajuste del modelo lineal a los datos (r2 = 0.9993). Para el ejemplo 2 (fig. 1 B), el ajuste exponencial parece ser adecuado (r2 = 0.9993). En este caso, los ajustes logarítmicos y polinómicos no son adecuados, pues presentan valores de r2 inferiores a 0.985. Un problema del procedimiento gráfico en este tipo de ejemplos es que el ajuste exponencial es adecuado para funciones del tipo ecuación 5 si α > 0, pero no es aplicable si α < 0. Esta limitación se solventa realizando el ajuste con Solver. En cuanto al ejemplo 3, se debe acudir a su resolución con Solver para ajustar los datos a la ecuación 3 o agregar una línea de tendencia polinómica de segundo grado (fig. 1 C). El tipo de ecuación propuesto para los datos del ejemplo 4 tampoco es ajustable con el procedimiento gráfico de Excel (fig. 1 D), y un ajuste polinómico carece de sentido químico en este caso. Otro de los inconvenientes de este procedimiento es que el programa se limita a ofrecer una ecuación sin incluir los errores de los coeficientes ajustados.
Herramienta de análisis de datos
La herramienta de análisis de datos de Excel es un complemento que debe ser activado a través de la ruta Archivo > Opciones > Complementos , seleccionando la opción Herramientas para análisis . Así se activa el complemento Análisis de datos del menú Datos . Dicho complemento contiene, entre otras herramientas, el análisis de regresión, que es aplicable solo a ajustes lineales. Al seleccionar Regresión , se abre un formulario de entrada donde se introducen los rangos en los que se encuentran los valores de x e y del ejemplo 1. Este formulario presenta opciones adicionales explicadas con detalle en una guía publicada en red por el primer autor (Jurado, 2008), pero en este tutorial nos centramos en las opciones por defecto. Tras introducir los datos y pulsar aceptar, se genera una hoja de resultados (fig. 2) con los valores del coeficiente de correlación, de determinación y de correlación ajustado, la varianza de residuales y el número de puntos ajustados que se muestran en las celdas B4, B5, B6, B7 y B8, respectivamente.
En el rango A10:F14 se tienen los resultados del análisis de varianza de regresión que calcula la probabilidad (F12) de que la varianza de regresión (D12) sea estadísticamente mayor que la varianza de residuales (D13). Valores bajos de probabilidad o muy altos de F (E12) implican un mejor ajuste del modelo. Excel denomina a las varianzas Promedio de los cuadrados . En las celdas B18 y B17 se encuentran los valores de pendiente y ordenada en el origen, con sus errores en las celdas C18 y C17, respectivamente.
Función ESTIMACION.LINEAL
Se trata de una herramienta muy potente para el análisis de regresión lineal y polinómica. Es una fórmula de las denominadas matriciales, es decir, que ofrece sus resultados en un rango de celdas formado por filas y columnas adyacentes. Una vez obtenido el resultado de una fórmula matricial, no se puede cambiar una celda sin modificar toda la matriz. Cualquier cambio en la fórmula que afecte a la matriz solo es efectivo si se pulsa al mismo tiempo "Ctrl" + "Shift" + "Enter".
Ajuste lineal
Para el ejemplo 1, partimos de una hoja con los valores de concentración en el rango A2:A5 y los de absorbancia en B2:B5. Se selecciona el rango B12:C16, y desde el menú Fórmulas se inserta la función ESTIMACION.LINEAL. En el formulario (fig. 3) se introducen los rangos de entrada para y (B2:B5) y para x (A2:A5). En el cuadro Constante se escribe VERDADERO (o el número 1) para que la función calcule la ordenada en el origen, o FALSO (número 0) para que la recta pase por el origen de coordenadas. En el cuadro Estadística , si el valor lógico es VERDADERO la función devuelve la estadística de regresión. Finalmente, se pulsa al mismo tiempo "Ctrl" + "Shift" + "Enter", obteniéndose la matriz de resultados de la parte inferior de la figura 3. Los caracteres escritos en las columnas A y D indican los datos que se encuentran en cada una de las celdas de la matriz: pendiente (B12) y su error (B13), ordenada en el origen (C12) y su error (C13), coeficiente de determinación (B14), desviación estándar de residuales (C14), valor del estadístico F (B15), grados de libertad (C15) y suma de cuadrados de regresión (B16) y de residuales (C16).
Ajuste polinómico
Se emplean los datos del ejemplo 3, situando los valores de intensidad fluorescente en B2:B12 y las concentraciones en A2:A12. Se selecciona un rango de celdas vacío de 5 filas y 3 columnas, A16:C20, y se inserta la función ESTIMACION.LINEAL. Para los valores de y se selecciona B2:B12, y para los de x se escribe A2:A12^{1,2}. En los otros 2 cuadros se introduce un 1 o el valor lógico VERDADERO. Una vez completado el formulario (fig. 4), se pulsa "Ctrl" + "Shift" + "Enter". Los coeficientes para el término cuadrático, de primer orden y el término independiente se obtienen en las celdas A16, B16 y C16, respectivamente, y sus errores en las celdas inmediatamente inferiores. En el rango A18:C19 se encuentran el resto de estadísticas de regresión.
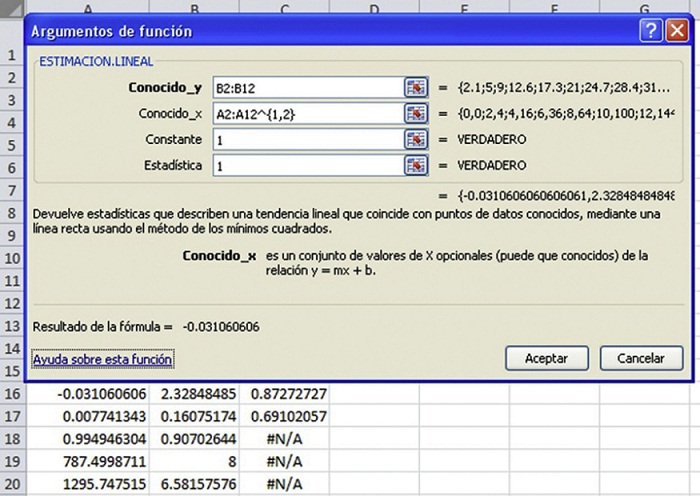
Figura 4 Formulario de la función ESTIMACION.LINEAL y resultados para el ajuste a un polinomio de segundo grado (ejemplo 3).
Cuando se emplea una configuración de idioma de Windows en español (México) la fórmula completa es =ESTIMACION.LINEAL(B2:B12,A2:A12^{1,2},1,1). En español (España), la fórmula queda =ESTIMACION.LINEAL(B2:B12;A2:A12^{1\2};1;1). En la versión de Excel 2007 los separadores en español (España) son siempre punto y coma, incluso para los grados del polinomio.
Si se quisiese ajustar un polinomio de segundo grado sin término de orden uno, para los valores de x se escribe A2:A12^{2}. De este modo se calcula solo el término cuadrático y el independiente. Si se quiere obviar el término independiente se introduce el valor FALSO, o número 0, en el cuadro Constante .
Función ESTIMACION.LOGARITMICA
Esta función ajusta los datos a una función del tipo ecuación 7, siendo aplicable solo para valores positivos de m y b . Cualquier base m puede escribirse como el número e elevado a una constante, con lo que puede aplicarse a los datos del ejemplo 2 con y = I y x=δ . Se estima así el valor e − β , obteniendo el valor de β como −ln(m) .
Se disponen los datos de x en A2:A9 y los de y en B2:B9, seleccionando las celdas del rango de salida A12:B16, y se inserta la función. En la figura 5 se observa el formulario completado y los resultados. En este caso, si el valor del cuadro Constante es FALSO o 0, se calcularía b=1 . El valor de m (A12) y b (B12) se obtienen con sus errores en la fila inmediatamente inferior. El resto de celdas en A14:B16 tienen el mismo significado que en ejemplos anteriores. A partir del valor de m obtenido, 0.7147 ± 0.0037, se calcula el valor de β , 0.3358 ± 0.0052, donde el error de β se obtiene aplicando la ley de propagación de errores a la ecuación que relaciona a ambos parámetros. Los resultados son similares a los obtenidos por el procedimiento gráfico (fig. 1B), pero incluyendo los errores de los parámetros de ajuste.
Estimaciones no lineales con Solver
Solver es un complemento incluido en Excel que permite optimizar el valor de una celda objetivo hacia un valor máximo, mínimo o especificado por el usuario, mediante la variación de los valores de una o varias celdas. En el caso de la regresión el objetivo es minimizar la suma de cuadrados de residuales variando los coeficientes de la función propuesta. Por lo tanto, habrá que calcular unos valores ŷ i para cada x i a partir de una función con unos parámetros de ajuste iniciales. Posteriormente se calculan los residuales y su suma de cuadrados, y se emplea Solver para minimizar esta suma variando los coeficientes. Las versiones de Excel anteriores a 2010 disponen de 2 algoritmos de optimización, el Simplex para problemas lineales y el Generalized Reduced Gradient (GRG) para ajustes no lineales. La versión 2010 incluye un tercer método, Evolutionary , que permite trabajar con datos no suavizados en problemas no lineales (Billo, 2007). En este tutorial se emplea GRG para resolver los ejemplos (2, 3 y 4) de regresión no lineal.
La figura 6 muestra la hoja de cálculo preparada para ajustar la ecuación 2 a los datos del ejemplo 2. Se disponen los datos de intensidad fluorescente en el rango A2:A9 y el espesor de estaño en B2:B9. En las celdas D19 y D20 se introducen unos valores de partida para los parámetros α y β , por ejemplo 155 y 0.4. Se escribe la fórmula =$D$19*EXP(-$D$20*A2) en la celda C2 y se copia en el rango C2:C9. El símbolo $ se usa para que al copiar la fórmula se mantengan fijas las celdas D19 y D20. En la celda D2 se calcula el residual como =B2-C2 y se copia la fórmula hasta la celda D9. En la celda D14 introducimos la suma de cuadrados de residuales (SC Res ) mediante la expresión =SUMA.CUADRADOS(D2:D9). Finalmente se llama al complemento Solver desde el menú de datos.
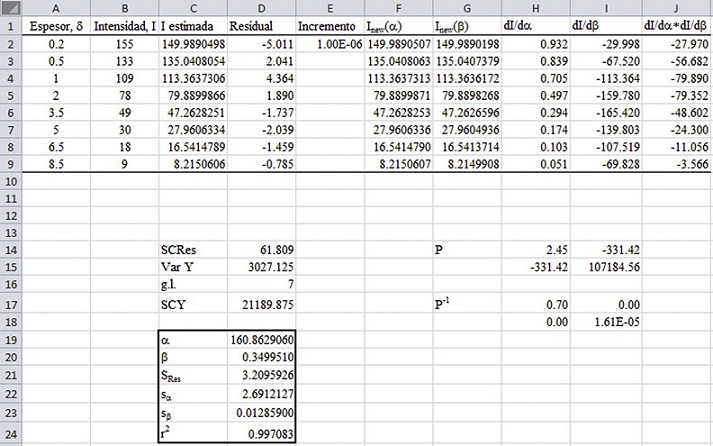
Figura 6 Aspecto final de la hoja de cálculo para el ajuste de los datos del ejemplo 2 mediante Solver y cálculo de errores.
El formulario de entrada de Solver presenta un cuadro Establecer objetivo , donde se escribe D14 (la suma de cuadrados), y en el cuadro Cambiando las celdas de variable se introduce D19 y D20 (los valores iniciales de los parámetros de ajuste). Se selecciona la opción de minimizar el valor de la celda objetivo y el método GRG Nonlinear , pulsando posteriormente en Resolver. Es importante desactivar la opción Convertir variables sin restricciones en no negativas cuando cualquiera de los parámetros a calcular en las celdas de variable tenga valor negativo. Si no se hace, Solver fuerza el cálculo de manera que esas celdas toman valor cero. Tomada esta precaución, se acepta y aparece un cuadro de diálogo que informa que Solver ha obtenido una solución. En la hoja de trabajo aparecerán las soluciones de Solver en las celdas donde estaban los valores iniciales.
El ajuste está solucionado, pero aún se desconocen los errores de los parámetros ajustados. Para obtenerlos se puede emplear un procedimiento basado en la diferenciación numérica de la función de ajuste respecto a cada uno de los coeficientes (Billo, 2007). Para una función general y=f(x) con k coeficientes de ajuste a i (i = 1 a k ), los errores σ i de los parámetros se obtienen de acuerdo a la ecuación 8.
donde S Res es la desviación estándar de residuales obtenida a partir de un conjunto de N puntos, como:
y P ii − 1 es el elemento que ocupa la posición ii en la matriz inversa de la matriz de derivadas parciales P = (P ij), formada por k filas y k columnas. Cada elemento P ij , donde i denota la fila y j la columna, se calcula como:
Los términos ∂f(x n)/∂ai pueden calcularse para cada valor x n mediante diferenciación numérica. Para ello, el coeficiente a i se varía en una pequeña cantidad Δa i manteniendo constantes los demás coeficientes a j . Con este nuevo valor del coeficiente a i el valor f(x n) inicial se transforma en un nuevo valor f'(x n), pudiéndose calcular para cada punto:
A partir de estos términos se obtienen los elementos P ij , se construye la matriz (Pij) y se invierte. Se emplean los términos de la diagonal principal de la matriz inversa para, mediante la ecuación 8, calcular los errores de cada parámetro de ajuste. Para el ejemplo 2 la matriz P queda:
En la hoja de cálculo la variación de α o β se introduce en la celda E2. Debe utilizarse un valor pequeño, y en principio el valor 10−6 parece razonable. En la columna F se calculan los valores de I estimado para un valor de α = α óptimo+Δα, manteniendo β=β óptimo . De este modo, en la celda F2 se escribe =($D$19+$E$2)*EXP(-$D$20*A2) y se copia en el rango F2:F9. En la columna G se hace lo mismo con β=β óptimo + Δβ y α = α óptimo , escribiendo en G2 =($D$19)*EXP(−($D$20+$E$2)*A2) y copiando en el resto de la columna. En las columnas H, I y J se calculan los términos de derivada parcial respecto a α , a β y el producto cruzado, respectivamente. Por lo tanto, en la celdas H2, I2 y J2 se escriben las fórmulas =(F2-C2)/$E$2, =(G2-C2)/$E$2 y =H2*I2, respectivamente, y se copian en el resto de la columna.
La matriz P (ecuación 12) se calcula en el rango H14:I15. En la celda H14 se introduce la suma de cuadrados de las diferenciales respecto a α mediante la fórmula =SUMA.CUADRADOS(H12:H9). La celda I15 contiene la suma de cuadrados de los diferenciales respecto a β , =SUMA.CUADRADOS(I2:I9). En las celdas I14 y H15 se introduce el sumatorio de los productos cruzados como =SUMA(J2:J9). La matriz H14:I15 se invierte en el rango H17:I18 seleccionando dicho rango, escribiendo la fórmula =MINVERSA(H14:I15) y pulsando "Ctrl" + "Shift" + "Enter".
Para calcular la desviación estándar de regresión (ecuación 9) en la celda D17 se escribe =RCUAD((D14)/(CONTAR(A2:A9)−CONTAR(D19:D20))). Se usa la función CONTAR para introducir el número de puntos N y el número de parámetros estimados, k , pero también podría introducirse numéricamente. La fórmula RCUAD, RAIZ, en Excel 2007 y anteriores, proporciona la raíz cuadrada de la celda seleccionada. Los errores de los coeficientes α y β se calculan en las celdas D22 y D23 como =RCUAD(H17)*D21 y =RCUAD(I18)*D21, respectivamente.
Para calcular el coeficiente de determinación es necesario conocer la suma de cuadrados totales de y respecto a la media. Esto es lo mismo que multiplicar la varianza de los valores y por los grados de libertad. En la celda D15 se calcula la varianza de y como =VAR.S(B2:B9) y los grados de libertad en D16 como =CONTAR(B2:B9)−1. En la versiones de 2007 y anteriores la fórmula de la varianza de una muestra es VAR. La suma de cuadrados de y respecto a la media se obtiene en la celda D17 como =D15*D16. Finalmente se calcula el valor de r2 en la celda D24 como =1−D14/D17.
Los resultados obtenidos son α = 160.863 ± 2.691 y β = 0.350 ± 0.013, con r2 = 0.99708. Este resultado varía un poco respecto al obtenido mediante el procedimiento gráfico (fig. 1 B). Esto se debe a que Excel, para el cálculo de la ecuación de ajuste mediante el procedimiento gráfico, emplea realmente la función ESTIMACION.LOGARITMICA y no un ajuste directo a una función exponencial del tipo ecuación 2.
Con fines comparativos, se realiza el ajuste aquí propuesto mediante el paquete de software estadístico comercial Statistica 8.0. En la tabla 2 se disponen los resultados obtenidos por ambos procedimientos con un número alto de decimales para apreciar las diferencias. Como puede observarse, se obtienen resultados muy similares para el ejemplo 2.
Tabla 2 Comparación de los resultados ± error de los parámetros ajustados mediante Solver y Statistica 8.0
| Ejemplo | Parámetro | Solver | Statistica |
|---|---|---|---|
| 2 | α | 160.8628 ± 2.69121 | 160.8630 ± 2.69118 |
| β | 0.34995129 ± 0.0128590 | 0.34995144 ± 0.0128586 | |
| r2 | 0.99708 | 0.99708 | |
| 3 | a | 63.2488 ± 8.7148 | 63.2490 ± 8.7151 |
| b | 0.01759 ± 0.0033147 | 0.01760 ± 0.0033148 | |
| r2 | 0.99298 | 0.99298 | |
| 4 | Vmax | 18.36381 ± 0.506229 | 18.36385 ± 0.506231 |
| Km | 42.98459 ± 2.336987 | 42.98462 ± 2.336989 | |
| r2 | 0.99699 | 0.99699 |
Los 2 ejemplos restantes, 3 y 4, están propuestos para que el lector los lleve a cabo por sí mismo. La resolución del ejemplo 3 es similar a la anterior, pero ajustando a una función del tipo ecuación 2. Se puede emplear la misma distribución de datos, coeficientes y demás parámetros que en la hoja propuesta para el ejemplo anterior, pero modificando las fórmulas de acuerdo al ajuste requerido. En este caso, en la celda C2 se escribe =$D$19*(1-10^(-$D$20*A2)), copiándose hasta C12. Se minimiza la suma de cuadrados de residuales con Solver con valores iniciales 40 y 0.02 para a y b , respectivamente. Los errores de los parámetros se calculan como en el ejemplo 2, empleando las fórmulas adecuadas en F2:G12. Los valores obtenidos en Excel, a = 63.25 ± 8.71, b = 0.018 ± 0.003 y r2= 0.99298, son muy similares a los obtenidos con Statistica 8.0 (tabla 2). En el caso del ejemplo 4 (ecuación 5), la ecuación de la celda C2 debe ser =$D$19*A2/($D$20+A2) y debe copiarse hasta C11. Se aplica Solver con unos valores iniciales de V max y K m de 18 y 40, respectivamente. Los resultados finales, V max = 18.5 ± 0.5 y K m = 43.0 ± 2.3 son muy similares a los obtenidos con Statistica 8.0 (tabla 2). Una hoja de cálculo con la resolución completa puede ser solicitada al primer autor.
Conclusiones
En el presente tutorial se han revisado las herramientas disponibles en Microsoft Excel para llevar a cabo cálculos de regresión. Se ha demostrado que la herramienta básica Agregar línea de tendencia está limitada a algunos tipos específicos de funciones, no permitiendo realizar ajustes definidos por el usuario. Además, las ecuaciones no incorporan información sobre los errores de los parámetros estimados. La herramienta Regresión es una macro que permite obtener información adicional, incluidos los errores de los parámetros estimados, pero solo se emplea en ajustes lineales.
La función ESTIMACION.LINEAL permite obtener los parámetros de regresión y sus errores y otros datos de regresión. La principal ventaja respecto a la macro Regresión es que se trata de una función y, como tal, puede ser insertada en una hoja de cálculo que irá variando su resultado automáticamente al variar los datos de entrada. Esta función permite además llevar a cabo ajustes polinómicos de distinto grado. La función ESTIMACION.LOGARITMICA realiza el ajuste a funciones del tipo exponencial de cualquier base m . Además permite obtener los errores de los parámetros de ajuste y otros datos de regresión. La función no es aplicable si alguno de los coeficientes es negativo, siendo este el principal inconveniente.
La herramienta Solver se puede usar para realizar cualquier tipo de ajuste lineal o no lineal. La gran ventaja es que permite llevar a cabo la estimación de parámetros de funciones definidas por el usuario. El principal inconveniente es que no proporciona los errores de los parámetros de ajuste, pero en el tutorial propuesto se incluye un posible método para llevar a cabo dicha estimación con buenos resultados.
Desde el punto de vista docente, los alumnos de química deben adquirir destreza en el manejo de herramientas informáticas de cara a mejorar su perfil laboral. Lo ideal sería implantar asignaturas de informática para químicos, aunque estas competencias también pueden ser desarrolladas en sesiones de prácticas de laboratorio, en seminarios de cálculo numérico o en prácticas en aula de informática. Otra opción es la organización de cursos de formación extracurriculares o la inclusión de tutoriales y prácticas resueltas como material online de libre disposición para los alumnos. Se pretende que este tutorial sirva de material de apoyo en este tipo de iniciativas.











 nueva página del texto (beta)
nueva página del texto (beta)


















