Introduction
Asthma is caused by a combination of genetic and environmental factors. It is a syndrome comprising different signs and symptoms such as cough, wheezing, shortness of breath, and chest tightness 1. Asthma is one of the most common diseases of childhood, causing substantial morbidity 2. More than 10 million children in the USA under age 18 (14%) have been diagnosed with asthma 3. According to Dorland's medical dictionary Small Airway Impairment (SAI) is a chronic obstructive bronchitis with narrowing of the bronchioles and small bronchi.
Pulmonary Function Testing (PFT) is of great importance in the evaluation and treatment of respiratory diseases. The advances in technology have culminated in the development of easier to use and commercially available PFT instruments that have been simplified in order to require minimal patient maneuvering and efforts 4.
Spirometry has been one of the most commonly used methods of assessing lung function in older children and adults 5. It has been demonstrated that both pre-school and school-age children have difficulty meeting some of the quality-control criteria outlined in the ATS/ERS guidelines when performing spirometry, and most pediatricians may profess that the critical period to evaluate pulmonary function is the infantile period, since this is the age of onset for childhood asthma 6. Objective measures for diagnosis and treatment of childhood asthma remain elusive 7, and the demand for an index applicable in a clinical setting for the evaluation of lung function in young children had been specified 8.
Forced Oscillation Technique (FOT) is the general name for airway mechanic measurement using the noninvasive superimposition of pressure waves on the subject's airway during normal tidal breathing. It has been noted however that a need for a practical FO index to define airway obstruction exists 9.
Impulse Oscillometry is one type of FOT. It is a promising pulmonary function testing method to diagnose and treat asthmatic preschoolers, but there is a need for more studies to be able to determine more precisely what IOS measures and what constitutes normal values 6-7. Impulse Oscillometry may be effectively employed in the diagnosis and management of diseases of the airways in children 10. IOS has also been recognized to be a useful diagnostic tool in early asthma development and could generate objective outcome measures of early interventions 11 -12. IOS should be considered as both an adjunct, and in some circumstances, as an alternative pulmonary function test to spirometry. It has been demonstrated that IOS has greater sensitivity and specificity in comparison to spirometry in identifying children with asthma and in determining their improvement after treatment on the basis of their bronchodilator responses 12, 13, 14. Other studies have established that IOS could be used to detect alterations in airway mechanics over the course of therapy not reflected by spirometry and that IOS may be capable of demonstrating airway growth-related changes over time 15-16.
Previous research by our group demonstrated that certain parameters of the equivalent electrical circuit models of the human respiratory system, the augmented RIC (aRIC) and extended RIC (eRIC), along with those of the IOS parameters have proven to be valuable in the diagnosis of patients with central and peripheral airway obstruction 16-17.
Reference Equations offer concise and compact quantitative means for evaluating the pulmonary function values of a single patient by comparing his or her data to the distribution of measurements in a reference population. Regression equations serve as effective and inexpensive alternatives to determine expected values of respiratory system measures as a function of height, weight, and age 18.
The purpose of this study was to determine predictive IOS Reference Equations based upon data acquired from 112 asthmatic and non-asthmatic Anglo and Hispanic children, 5-17 years old, in order to provide an original frame of reference for different IOS and respiratory system model parameters within this population.
The present article is the first in publishing IOS Reference Equations for Anglo and Hispanic children 5 to 17 years old as well as the first in calculating Reference Equations for IOS-based respiratory system model parameters (eRIC-Rp and eRIC-Cp).
Methods
Subjects
IOS pulmonary function testing was performed in Anglo and Hispanic children 5-17 years old living in El Paso, Texas. The data were collected at Western Sky Medical Research Clinic and at a Health Fair held at an elementary school located in the city's Socorro school district in 2006. The acquired data were then analyzed by our expert clinician and classified into four categories: Normal, Probable Small Airway Impairment (PSAI), Small Airway Impairment (SAI), and Asthma. A total of 112 children, 5 to 17 years of age were tested: 52 females and 60 males. The University of Texas at El Paso (UTEP) Institutional Review Board (IRB) approved the research protocol. An informed consent form was given to every parent and their child, providing them with a detailed description of the study. The study's population demographics (Age, Standing Height, and Weight) are shown in Table 1.
Figure 1 shows the frequency distribution of all the study population function of Height (cm).
Regression equations
Regression analysis was used in the determination of the Reference Equations for this population. The use of bivariate linear regressions provided the best prediction models with higher significance of independent variables, better than Multivariate linear equations.
One approach to perform regression analysis is to use separate simple regression equations for several different age groups. The square of the correlation coefficient (r2) and the Standard Error of the Estimate (SEE) are the most common measures of how well the regression equations fit the data they describe. The proportion of variation in the observed data represented by the independent variables is measured by r2. The SEE is the average Standard Deviation (SD) of the data around the regression line. As regression methods reduce the differences between the predicted and observed pulmonary function measures in the reference population, the values of SEE will decrease and r2 will increase 18).
IOS measurements
Impulse Oscillometry measures Pulmonary Impedance (Zr) during normal tidal breathing of a subject. Zr is comprised of Resistance (R) and Reactance (X) components, which are 90 electrical degrees out of phase. Resistance is indicative of the energy required to propagate the pressure wave through the airways and Reactance is reflective of the amount of recoil generated against that pressure wave. The Reactance comprises forces of inertia resulting from the air movement in the conducting airways and the elastic recoil of the lung tissue. R and X are measured in either units of cmH2O/L/s or KPa/L/s. IOS! measures pulmonary function over a range of frequencies from 5 to 25 Hz (cycles/sec). Acoustic waves with lower oscillation frequencies, such as 5 Hz, travel farther to the lung periphery and provide indices of the entire pulmonary system, whereas waves with higher frequencies, such as 20 Hz, provide information primarily related to the central airways. Increasing evidence shows that the peripheral airways have an important role in asthma control; however none of the traditional tests (e.g. Spirometry) specifically measures the peripheral airways. IOS is increasingly being used to separately measure the degree of central and peripheral airway obstruction. Resistance at 5Hz minus Resistance at 20 Hz (R5-R20) has been used as an index of frequency dependence of resistance (fdR), representing peripheral airways obstruction. Frequency dependence of resistance is inversely proportional to age: the younger the child, the greater the R5-R20 value 10, 19. The Resonant Frequency (Fres) is the point at which reactance is zero. The Reactance Area (AX), also called the "Goldman Triangle", is the integrated low frequency respiratory reactance magnitude between 5Hz (X5) and Fres. AX is a single metric that reflects changes in the degree of peripheral airway obstruction and closely correlates with fdR 20.
For this study, a Jaeger MasterScreen IOS (Viasys Healthcare, Inc. Yorba Linda, CA, USA) was used. The system was calibrated every day before data collection using a 3-L syringe for volume calibrations and a reference resistance (0.2 kPa/L/s) for pressure calibrations. Children were asked to wear a nose clip, while breathing normally through a mouthpiece, and were instructed to close their lips tightly around it to avoid air leakage. Three to five IOS test replicates were performed on each subject to ensure reproducible tests without artifacts caused by air leaks, swallowing, breath-holding, or vocalization. In each IOS test impulses were applied for a period of 30 to 45 seconds. IOS data were carefully reviewed offline and quality assured by our group's resident expert clinician who rejected segments affected by airflow leaks or swallowing artifacts.
Respiratory Impedance Model
Extended RIC (eRIC) Model:
This model was developed as an improvement to the RIC model with an additional peripheral Resistance (Rp) connected in parallel with the Capacitance. Therefore, the eRIC model is composed of central (large airway) Resistance (Rc), large airway Inertance (I), peripheral (small airway) Compliance (Cp), and peripheral (small airway) Resistance (Rp). This added Rp allows for the frequency dependence of Resistance observed in impedance data. Figure 2 shows the eRIC model circuit.
Data analysis
The average values of the IOS and eRIC model parameters were used in this study to determine the Regression Equations for the four groups: Normal, Probable Small Airway Impairment (PSAI), Small Airway Impairment (SAI), and Asthma. All of the statistical analyses in this study were performed using SPSS 22 Software (SPSS Inc., Chicago, IL, USA).
These equations were generated using simple linear regression analysis with Height, Age, and Weight as independent variables.
Results
Reference values are important indexes in establishing whether an individual's measured values fall within a range to be expected for a healthy person with similar height and age. Most of the previous studies performed to provide reference values for FOT and IOS parameters for children were designed for preschool children 21-28, as IOS has been proven to be of high significance in the assessment of the pulmonary system in this population. Attractive practical features such as: effort-free operation, minimal passive cooperation from the subject wearing a nose clip while keeping tightly closed lips around a mouthpiece, and breathing normally through the mouth make the IOS a popular lung function test for small children who are unable to perform spirometry. Studies by other researchers have generated FOT and IOS Reference Equations for 2-20 year-old children and young adults 29-33, which are comparable to the results in the present study.
Table 3 presents a summary of the studies performed using the Impulse Oscillometry technique to generate Reference Equations for children 23-28, 31-33.
A recent study by Hagiwara et al. 34 was published showing Reference Values for Japanese Children (6-15 years). In this study the authors presented R5, R20 and R5-R25 Reference values according to height in terms of standard deviation calculated with the lambda-mu-sigma (LMS) method. As only IOS Reference values and standard curves, for the mentioned parameters, were presented and Reference Equations were not calculated, as in previous studies 21-33, it was not possible for us to include that study in our Table 3.
Also Santos Schivinski et al. 35 recently reported IOS Reference Equations for Brazilian Healthy children and adolescents. They tested 864 healthy school students aged 6 to 14 years old. Only an abstract has been published on this research and no Reference Equations were given.
In our previous work, we have demonstrated that there are no significant differences between genders 36 and between ethnic groups in this population 37. We did not observe gender or race significant differences in the same manner in our investigation as it was demonstrated in previous studies 24-25, 27.
In the present study Reference Equations for IOS and eRIC model parameters were generated based upon IOS data acquired from 112 children, previously classified by our expert clinician, the late Dr. Michael Goldman, into four groups: Normal, PSAI, SAI and Asthma. The Normal Group was composed of 11 children, PSAI of 17 children, SAI of 54 children and Asthmatic of 30 children, respectively. In Table 2, the demographics for each group are presented.
In Table 3 the following information is presented: r = correlation coefficient, r2=coefficient of determination (the fraction of the data that is the closest to the line of best fit), R = Resistance (kPa/L/s), X = Reactance (kPa/L/s), AX = the Goldman Triangle (kPa/L), Height (meters or centimeters), Age (years or months), and Weight (kilograms) for the mentioned studies using IOS 23-28, 31-33.
Our linear regression analysis indicated that IOS variables were well correlated with both Height and Age, as found by Amra 31 and Gochioca-Rangel 33, but most strongly associated with Height as has been shown in previous studies (23-29, 32). The Reference Equations generated in the present study as a function of Height are presented in Table 4 for Normal, Table 5 for PSAI, Table 6 for SAI, and Table 7 for Asthmatic children respectively; where r2 = the coefficient of determination and SEE = the Standard Error of the Estimate.
Discussion
In contrast to our research, the study performed by Frei et al. 24, presented Reference Equations for solely white North American children (3-10 years) with two white parents.
Our study is the first in publishing IOS Reference Equations for Anglo and Hispanic children 5 to 17 years old. Also is the first study in calculating Reference Equations for IOS-based respiratory system model parameters (eRIC-Rp and eRIC-Cp). One of the advantages of our Reference Equations is that most of the significant IOS and model parameters resulted in r2 values higher than 30%, with some of them reaching up to 60% and even to 80%, whereas previous studies reported r2 values lower than 20% 26-27.
The regression equations with r2 values higher than 0.4 are highlighted in bold in Tables 4 to 7. In the Normal Group, it can be observed that the resistance values R5 to R20 and R5-R20 present the highest r2 values, showing these to be good predictors of normal parameters. In the PSAI, SAI, and Asthma Groups R5, X5, X10, X15, R5-R20, AX eRIC-Rp and eRIC-Cp have the greatest r2 values which seem to indicate that these parameters are the best predictors for children with respiratory impairments. These results seem to confirm what Nowowiejska et al. have previously concluded 32 by showing that reactances manifested greater specificity compared to resistances in assessing bronchial obstruction in children.
One of the limitations of our study was that the Normal Group included solely sample data from children 11-17 years old. This could be the reason why our R5 regression coefficient was lower than those reported in previous studies by other researchers 24-27. However, in spite of this limitation, it is clear that Resistance values decrease with Height and Age as expected.
In Figure 5, the reference equation for R5 as a function of Height was compared with those generated in previous studies, which utilized simple linear regression equations to represent their data. Our data are close to those acquired by Nowowiejska et al. 32, who utilized a wider age range than the ones used in other studies, and it seems that the equations generated by Frei et al. 24, Park et al. 26, and Lai et al. 28 could have been similar to ours if we would have been able to include data from younger normal children with lower heights.
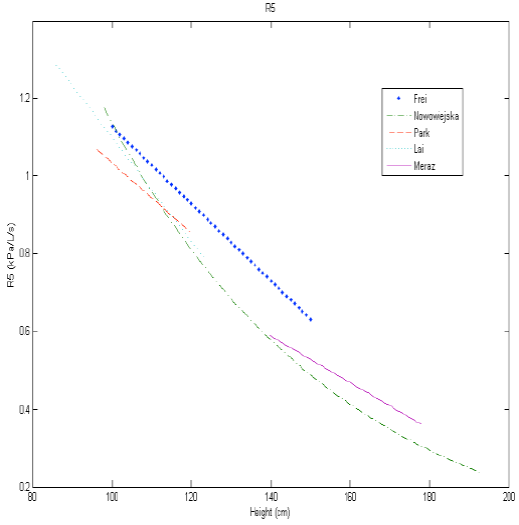
Figure 5 A comparison of the relationship between R5 and Height in our study and those of Frei, Park, Lai and Nowowiejska 24, 26, 28, 32.
It can be observed in Figure 6 and Figure 7 that R5 increases with respiratory impairment severity, from normal to PSAI to SAI and Asthma. It can also be noticed that X5 decreases with SAI and Asthma severity, in the same progression as expected. In a similar manner, Figure 8 shows that AX increases with respiratory impairment severity.
Conclusions
Impulse Oscillometry can serve as a sensitive pulmonary function test performed in younger and older children to diagnose asthma and other pulmonary conditions with relative ease and without requiring extreme breathing maneuvers and bronchoprovocation. It has been proven to be useful in the assessment of respiratory impairments. Our investigation reported here provided IOS and eRIC model parameter Reference Equations for four groups of Hispanic and Anglo children: Normal, PSAI, SAI and Asthma. These equations could be used in the future to provide a quantitative framework for indication of illness progression, or as a reference tool to diagnose the degree of respiratory system impairments in children in the 5 - 17 year-old age group.
This work showed and validated that Height was the best determinant of IOS variables. Resistance (R) correlated negatively with Height, while Reactance (X) correlated positively as previously seen in the literature.











 nueva página del texto (beta)
nueva página del texto (beta)
















