INTRODUCTION
Gait analysis has been used to evaluate different conditions in sport sciences, biomechanics and clinical diagnosis [1]. In clinical environments, this assessment tool has been applied to diagnose: hemiplegia [2], Achilles tendinopathy [3], inversion sprains [4], Parkinson's disease [5], hip arthroplasty [6], knee osteoarthritis [7], idiopathic scoliosis [8], cervical myelopathy [9], among others. In the same way, gait analysis has allowed to estimate the progress of patients rehabilitated after a stroke [10]; or simply to determine the joint displacement in the hip, knee and ankle [11] [12]. In this paper, we focus on studying the kinematics of the lower limbs in human gait based on quaternions algebra.
On the other hand, quaternions are useful to perform a rotation of vectors in a 3D space [13]. Today, they are widely used in computer graphics, multirotor tracking and control approaches, and kinematics and dynamics of rigid bodies [14]. Therefore, the free representation of the quaternions in the Euclidian space has also been used in navigation, computer-aided design and computer vision [15].
Recently, interest in robotic developments has been increased. The most well-known methods for robot kinematics are the Denavit-Hartenberg convention [16] and geometric methods [17]. Therefore, most of the work done to model robot kinematics using quaternions continues to follow the D-H approach, wasting quaternions capacity [15]. Some robotic applications have been focused on gait approaches to establish the imitation of human gait. For example, a robotic platform for the kinetics and kinematics characterization during gait has been used [18]. Therefore, mathematical models that associate forward kinematics of position are required [19]. For this reason, in this work we present a theoretical approach for modeling forward kinematics of position of the lower limbs for human gait using quaternions algebra not based on the D-H convention.
Related work
Some methods have been proposed in the literature for the three-dimensional analysis of gait kinematics using wearable sensors and quaternions algebra [20] [21]. In the first work, the initial orientations are computed by quaternions of the inertial sensors placed in pelvis, femur, tibia and foot, which are acquired from the acceleration data, while the angular displacement is defined from the angular velocity. Subsequently, the orientations of the independent body segments are obtained from the sensor’s orientation and the calibration rotation matrix, to then synthesize a 3D model of the whole body concerning the global reference frame. Similarly, the algebra-based position of quaternions of the frame of each joint is obtained from the gyroscope and the accelerometer signals [21]. Therefore, in addition to the existence of position estimation error derived from the use of inertial sensors, in both works, there is a low performance in the gait analysis, since anthropometry is not directly considered and, the joint system is handled by an independent structure and not as a serial chain.
On the other hand, in the work [22], a local analysis of the stability of the joints during walking is carried out using a marker-based optical system. This implies that forward kinematics of position is also obtained from the position of the markers and the calibration test [5] [6] [7]. In addition to what has been mentioned in this section in the aforementioned works, only the hip, knee and ankle are analyzed, that is why, to have greater precision in the kinematic calculation of gait, it is necessary to include the rotational and tilting movements of the pelvis.
Problem statement
Generally, the normal gait pattern is established in the joint space [23] and independently from each anatomical movement of each joint structure. Which limits the global perception of the performance of the joint system and the use of well-known metrics such as speed, cadence and stride length, which are established in the operational space (gait space) and are related to anthropometry of the individual. Therefore, the calculation of direct kinematics is necessary to determine the gait pattern in cartesian space as a function of joint variables.
Although the well-known Denavit-Hartenberg DH [16] convention and geometric [17] methods can solve well the forward kinematics of position in the sagittal plane of the 3 DoF joint system of the lower limbs (Figure 2), if the number of degrees of freedom of analysis in the transversal and frontal planes is increased as in the 8 DoF system (Figure 3), these methods require a more complex mathematical modeling and are less flexible in the description of the evolutions of the system of the extremities with respect to the orthonormal frame of reference. Therefore, a method of lower mathematical complexity, with a low computational cost and that requires little storage capacity [15] is required for the analysis of the gait in cartesian space as the one proposed in this contribution.
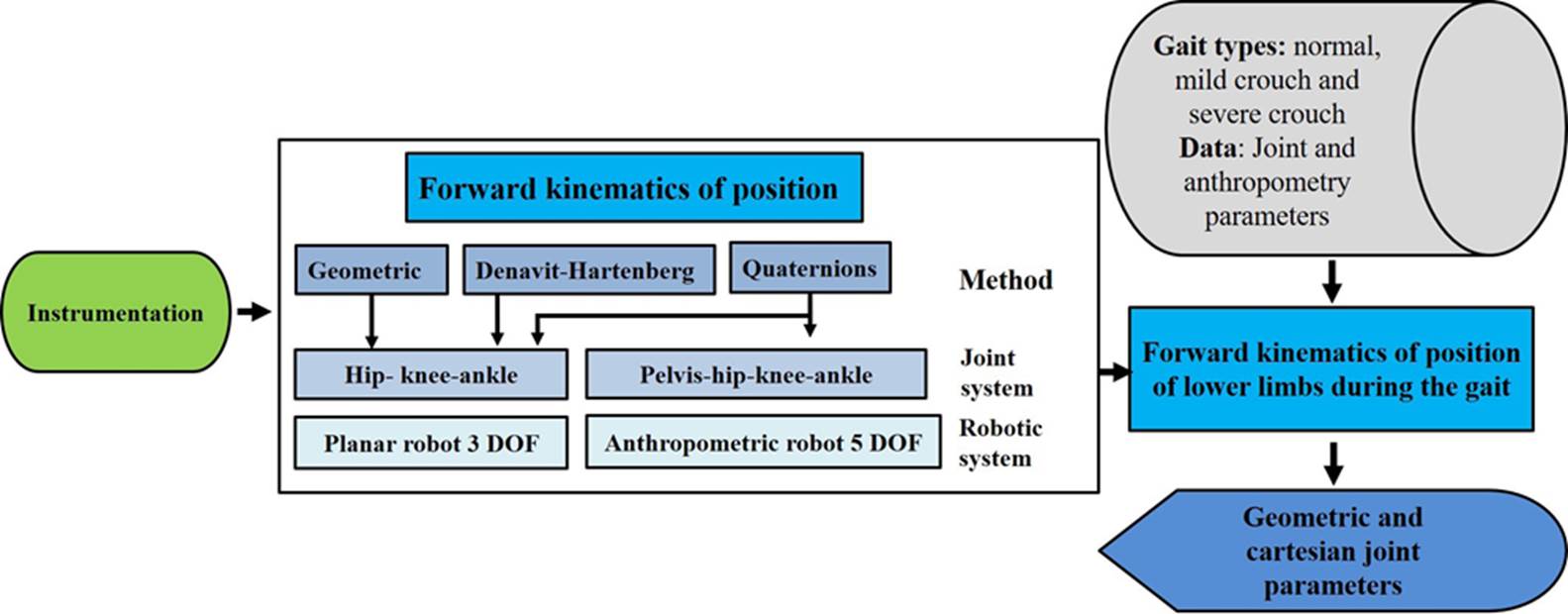
Figure 1 Methodology for the modeling and visualization of the forward kinematics of position of the lower limbs during gait using methods: i) geometric, ii) Denavit-Hartenberg and iii) quaternions for joint and anthropometry variables established in [20] and [24], respectively.
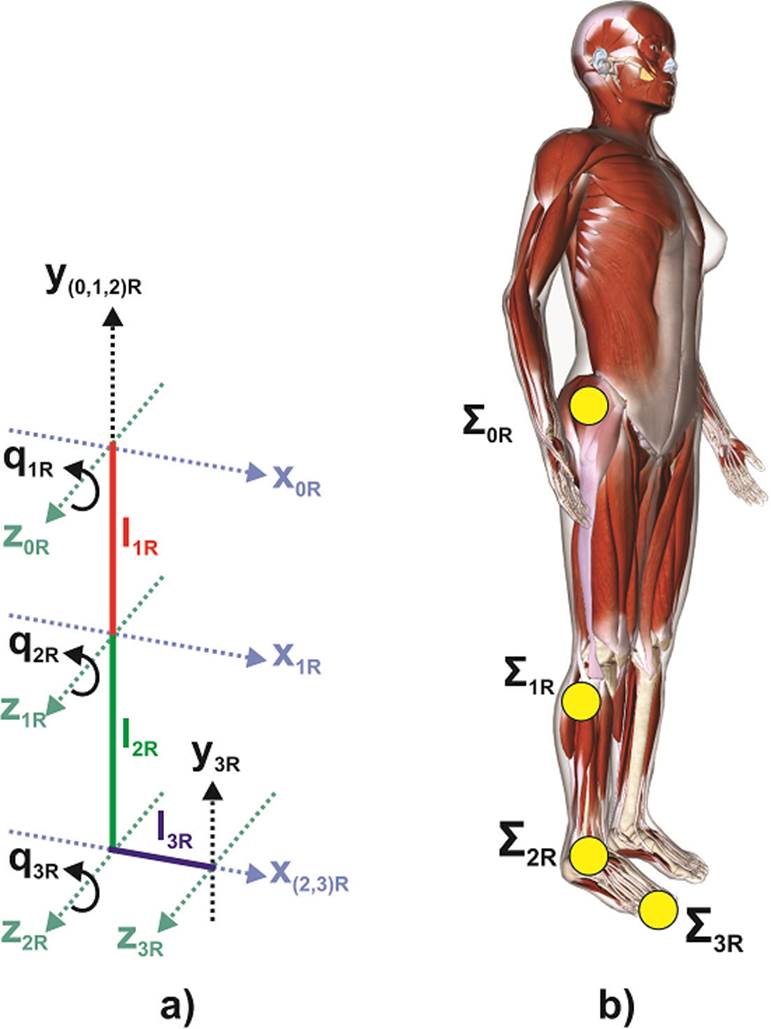
Figure 2 a) Open kinematic chain that represents the frames that define joint movements in the sagittal plane. Correspondence of the frames to the musculoskeletal reference points in the female model [27].
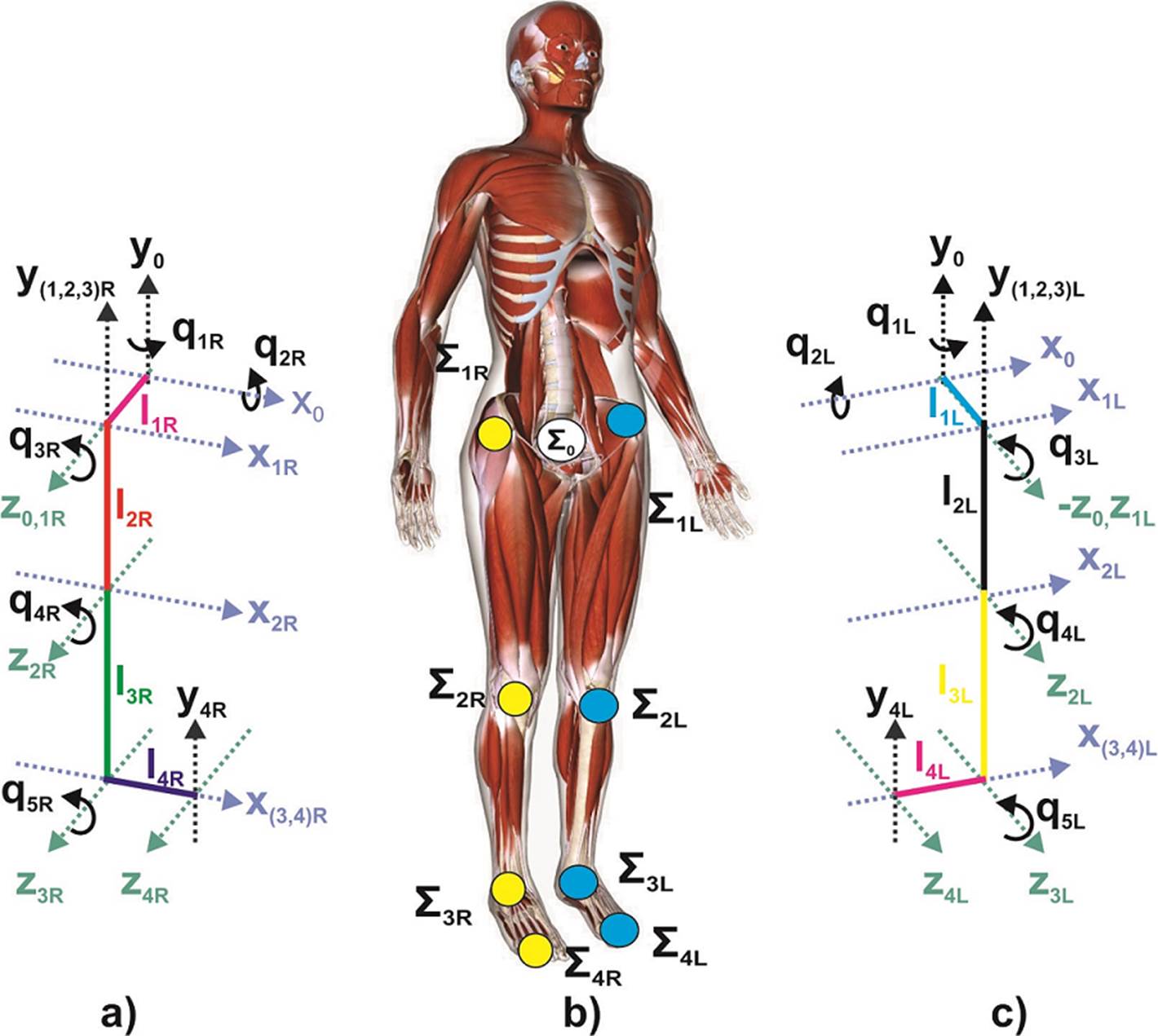
Figure 3 Proposed kinematic chain representing the frames that define the movements of the joined system for gait modeling. a) Lower right limb, b) Correspondence of the frames and reference points in the female musculoskeletal model [27] and c) Lower left limb.
Proposed solution
In this work, a method to calculate the forward kinematics of position of the articular system of the lower limbs during gait, using quaternion algebra as a mathematical tool is proposed. To this end, the modeling of the articular system of the lower extremities is established as an open serial chain, which allows obtaining a global performance of the system and a reference pattern of normal gait in the operational space. Also, the analysis in the gait space allows the evaluation of the metrics of that space and some not common metrics for this purpose such as: the Euclidean distance, the areas and the centroid between each reference. Finally, to evaluate abnormal performances in the cartesian space for reference pattern, a comparative analysis is performed in the 3 anatomical planes for a normal gait and 2 types of crouched gaits, of which their forward position kinematics is calculated from the articular anatomical positions related to the rotation and inclination of the pelvis, dorsiflexion of the hips and knees, as well as dorsiflexion and plantarflexion of the ankles.
Paper organization
In this work, the anthropometry and the joint parameters considered as the starting point are adapted to [20] and [24], respectively. Subsequently, mathematical modeling is proposed to calculate the forward kinematics of position of the 3 DoF lower limbs joint system (Figure 2), which directly considers anthropometry, using the methods: i) geometric, ii) DenavitHartenberg and iii) quaternions. Later, due to the increase in complexity, the modeling of the forward kinematics 8 DoF system (Figure 3) is developed using quaternions, a simulation of the kinematics is performed and the cartesian coordinates and joint variables of both extremities are visualized. Finally, a metric based on the Euclidean distance between both ends of the feet (big toe), ankles and knees are calculated.
To describe the work done, this paper is organized as follows: Related work, problem statement and proposed solution are described in the introduction section. In the materials and methods section, the mathematical modeling for the calculation of the forward kinematics of position of joint systems and lower limbs using the methods: i) geometric, ii) DenavitHartenberg and iii) quaternions algebra, is presented. The analysis and discussion of results is shown in the corresponding section and finally, the last section focuses on the conclusions.
MATERIALS AND METHODS
Kinematics is the study of the motion of mechanical systems without regard to the cause of the motion. The most well-known methods for forward kinematics of position of robots are the Denavit-Hartenberg convention [16] and geometric [17] methods. In this work, the lower limb joint system is considered as a set of rigid links connected together at various joints during the swing phase of the gait cycle. Therefore, the methodologies used in robotics such as: i) geometric method ii) D-H) and iii) quaternions [25], can be used to calculate the forward kinematics of position of the lower limbs during gait, which is described as follows.
Forward kinematics of lower limbs
Hip - knee - ankle system (HAK)
To develop the kinematic analysis in this work, the anatomical terms describing the relationships of the different parts of the body are based on the anatomical positions of sagittal, frontal and transverse planes; and their main directions [23]. Firstly, we develop a synthesis of forward kinematics of position of 3 DoF system as a planar robot, whose home position in (Figure 2) of the first link is on the y0R (-) axis of the origin of the base frame OΣ0R, and the origins of the orthonormal frames of the robot correspond with the reference points of the joints of the human's lower right limb model (Table 1). In this case, the anatomical sagittal plane corresponds to the x-y plane of the robot, while that z0R (+), x0R (+) and y0R (+) axes correspond to the right, front and top directions, respectively [23]. The model features lower limb right joint as 3 rigid-body segment 1) femur, 2) tibia and 3) foot and the anthropometry is adopted from [20]. The relative motion of these segments is defined successively by quaternions algebra.
Table 1 Correspondences between the orthonormal frames of the 3 DOF planar robot and the join references of the body (Figure 2).
| Orthonormal cartesian frames |
Joint references of The right lower limb |
|---|---|
| OΣ0R (x0R, y0R, z0R) | Hip |
| OΣ1R (x1R, y1R, z1R) | Knee |
| OΣ2R (x2R, y2R, z2R) | Ankle |
| OΣ 3R (x3R, y3R, z3R) | Big toe |
Let, l1R, l2R, l3R, Q1R, Q2R and Q 3R the anatomical length dimesions of femr, tibia and foot, and the flexion-extension angles of the hip and knee, as well as dorsiflexion and plantarflexion of the ankle, of the right lower limb, respectively. Then, if we consider symmetry for the left limb it is possible to apply the methods mentioned in the previous section to get forward kinematics of position for both right (denoted by subscript R) and left (denoted by subscript L) limbs. Commonly, hip, knee and ankle have only been used to analyze the gait kinematics [11] [12] [20] [26].
In a 3 DoF planar robot, the width of each servomotor and the thickness of the joint bar are determined by β1R, β2R and β3R, for simplicity in this case, these values are equal to 0. The placement of the ziR axes coincide with the axes of rotation of the joints, while the xiR axis is assigned in the direction of the link and the yiR axis according to the right-hand rule. Meanwhile, q1R, q2R and q3R are the hip and knee flexo-extension, and ankle dorsiflexion and plantarflexion, with respect to the z0R, z1R and z2R axis, respectively.
Geometric method
The position of the right big toe [x3R, y3R, z3R] ϵ R3x1 T without orientation, could be obtained geometrically adding a link in the x0R axis direction, whose joint is arranged in the Σ2R frame origin (Figure 2) [17], such that, the coordinates of such position are determined as
where cqiR and sqiR are the cosine and sine transcendental functions that depend on qiR, respectively.
Similarly, the position of the left big toe could be obtained by the D-H convention.
Denavit - Hartenberg convention
If we assume the same configuration (Figure 2), by means of the D-H convention [16] the parameters of the joints and the links of the right lower limb are shown in (Table 2).
Table 2 Denavit-Hartenberg parameters for the HAK system (Figure 2).
| linki | θi | di (βi) | li | α i |
|---|---|---|---|---|
| 1 |
|
β1R | l1R | 0 |
| 2 |
|
β2R | l2R | 0 |
| 3 |
|
β3R | l3R | 0 |
Thus, the homogeneous transformation matrices for each link can be written as
Then, applying trigonometric identities D-H procedure [16], the generalized homogeneous transformation matrix results as
where x3R, y3R and z3R are equivalents to the Equation (1), Equation (2) and Equation (3) of the geometric method. Therefore, the end position of the point OΣ3R (x3R, y3R, z3R) is the same using the geometric method and the D-H convention.
Quaternions-based forward kinematics
The four-dimensional space H is formed by the real axis and three orthogonal axis, spanned by the principal imaginaries vectors i = (1,0,0), j =(0,1,0) and k = (0,0,1), which obey Hamilton rules [28]: i2 = j2= k2 = ijk= -1. Where multiplication of these imaginaries resembles cross product, such that ij= k, jk= i, ki= j, ji= -k, kj= -i, ik= -j.
A quaternion Q= r + xi + y j + zk consists of a real part r and a pure part v = xi + yj + zk[13]. Let Q1= a1 + v1 and Q2= a2 + v2 two quaternions, then, their product is calculated using the dot product and the cross product as:
The quaternion Q= a+v also decomposes into a+bu, which resembles a complex number, where the imaginary u is a unit-three vector
Thus, |(|u |)|= 1 and x,
y, z are the cartesian coordinates of
v. Let Q=
a + bu, so its conjugate
is
On the other hand, a rotation of θ around axis u is represented as the unit quaternion.
Given a unit quaternion Q that represents a rotation, then, the rotation around an arbitrary pure vector v ϵ R3 is
where
Then, if we represent the HAK system (Figure 2), by quaternions algebra, from Equation (10) the quaternion representation of the rotation around the z0R axis is
Where u1R = [0, 0,
0, k] is a unit vector, q1R is
the rotation angle around the
z0R axis and OΣ
is the rotation angle around the
z0R axis and
OΣ1R = [0, 0,
-l1R
j, 0] is the representation of the home
position of the frame Σ1R origin. Then, the
rotated final from
OΣ1R using
Equation (11) is
Let us
the quaternions representing rotations with angles q2R and q 3R around z1R and z2R axes, respectively. u2R = [0, 0, 0, k ], u3R = [0, i, 0, 0], OΣ2R = [0, 0, l2R j, 0] and OΣ3R = [0, l3R i, 0, 0], then, in a recursive form the final position daring the gait cycle of the right could be written as
For example, for a specific case where q1R = q2R = q3R = 0, l1R = l2R = l3R = 1 and β1R = β2R = β3R = 0 we get OΣ3Rf = [0, 2, -2j, 1], which corresponds to the same result though geometric method and D-H convention.
Pelvis - hip - knee - ankle system (PHAK)
In this section, to improve the kinematic gait analysis, in addition to the movements of flexion-extension of hip and knee, as well as dorsiflexion and plantarflexion of ankle [11] [12] [20] [26], rotational and tilting movements of the pelvis are added to the previous model (Figure 2). The two lower limbs are simultaneously considered as open serial kinematic chains and the reference frames are reassigned as shown in (Figure 3). For this reason, it is possible to calculate the forward kinematics of position of the joints and big toes of both lower limbs using the previously described methods. However, geometric methods and classical D-H convention become more complex as degrees of freedom increase [16] as in this model. While the quaternion-based method presented as following, represents a flexible and precise tool for this approach.
In system PHAK (Figure 3), the model features the lower limbs as 7 rigid-body segments 1) pelvis, 2) right femur, 3) left femur, 4) right tibia, 5) left tibia, 6) right foot and 7) left foot. The relative motion of these segments is defined successively by quaternions algebra. The anthropometry is adopted from [20]. The cartesian frames Σ0, Σ1, Σ2, Σ3 and Σ4 correspond to the references placed on pelvis, hip, knee, ankle and big toe, respectively, in both lower limbs. Let us define the origin of the cartesian frames as a quaternion as OΣ1R = [0, 0, 0, l1R k], OΣ2R = [0, 0, -l2R j , 0], OΣ3R = [0, 0, -l 3Rj , 0], OΣ4R = [0, l4R i, 0, 0]. The quaternions Q1R, Q2R, Q3R, Q4R and Q5R with u1R = [0, 0, j , 0], u2R =[0, i, 0, 0], u3R= u4R = u5R = [0, 0, 0, k], is the quaternions representation of the rotation and tilting movements of the pelvis, flexo-extension of hip and ankle, as well as dorsiflexion and plantarflexion of ankle, respectively. Finally, l1R, l2R, l3R and l4R, are related with the lengths of pelvis, femur, tibia and foot. Thus, recursively the position of the right big toe is calculated from Equation (11) as
Similarly, the position of the left big toe could be calculated and expressed as:
Once the forward kinematics of the position of both lower limbs has been obtained, a simulation and visualization corresponding to the HAK (Figure 2) and PHAK (Figure 3) systems are carried out for the types of gait: i) normal, ii) mild crouch and iii) severe crouch. The computational implementation on Matlab® of the quaternions method to calculate the forward kinematics of position of the PHAK system is represented in the following flow chart (Figure 4). In the same way. the algorithm is applicable for the HAK system.
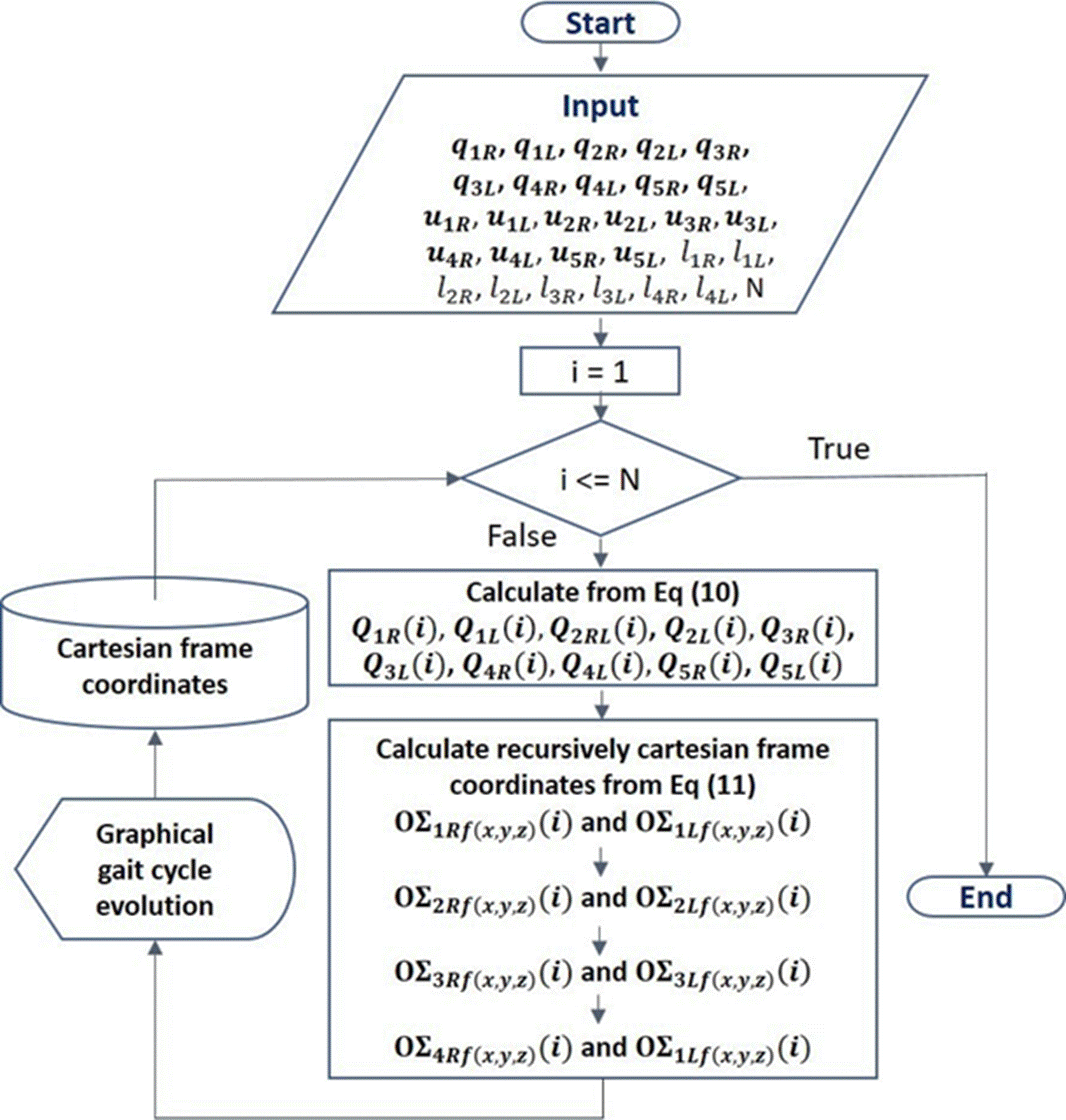
Figure 4 Flowchart for the computational implementation for the forward kinematics of position using quaternions algebra.
Where, the input data q1R, q1l, q2R, q2L, q3R, q3L, q4R, q4l, q5R, q5l are the values of the angles for rotation and tilt of the pelvis, flexo-extension of hip and knee, as well as, dorsiflexion and plantarflexion of the ankle, for both extremities, respectively. N is the number of samples per gait cycle. These values were adopted from de gait2392_simbody model [24] for each gait (Table 4). This model is a three-dimensional, 23-degree-of-freedom computer model of the human musculoskeletal system. While, l1R, l1L, l2R, l2L, l3R, l3L, l4R, l4L, pelvis, femur, tibia and foot anthropometry was adopted from [20]. The proposed method in this work allows a flexible and transparent coupling of the joint angles and anthropometry to determine the forward kinematics of position. u1R, u1L, u2R, u2L, u3R, u3L, u4R, u4L, u5R, u5L were proposed according to the configuration of the model in (Figure 3).
Table 3 Movement models used from gait2392_simbody.osim [24] .
| Gait type | Movement model |
|---|---|
| Normal (N) | normal |
| Mild crouch (MC) | crouch1 |
| Severe crouch (SC) | crouch4 |
Next, iteratively for all the sampled of the gait, based on Equation (10), the quaternions that represent each corresponding movement are calculated. And sequentially from Equation (11), the positions of each joint reference are calculated.
Finally, for each iteration a graphic representation of the pattern of each type of gait in that corresponding sample can be made. The data of the cartesian positions of each joint are stored to be compared later.
RESULTS AND DISCUSSION
In this section, the most relevant results of this work are presented and described. Then, in order to present the movement pattern of the gait model [24] (Figure 4a) and the one proposed in this work (Figure 4b), visualizations in the sagittal plane of 6 states (0, 20, 40, 60, 80, and 100) % of a normal gait cycle for both methods are shown. The values of the angles and anthropometry used are those described in the previous section. To highlight part of the contribution of this work, we include the visualization of the same states and conditions for the same gait for the frontal plane (Figure 5) and the superior transverse plane (Figure 6), in which it is possible to appreciate rotating and tilting movements of the pelvis, respectively. These movements have been included in this work unlike others that have not, which substantially improves the precision in the calculation of the kinematics of the lower limbs.
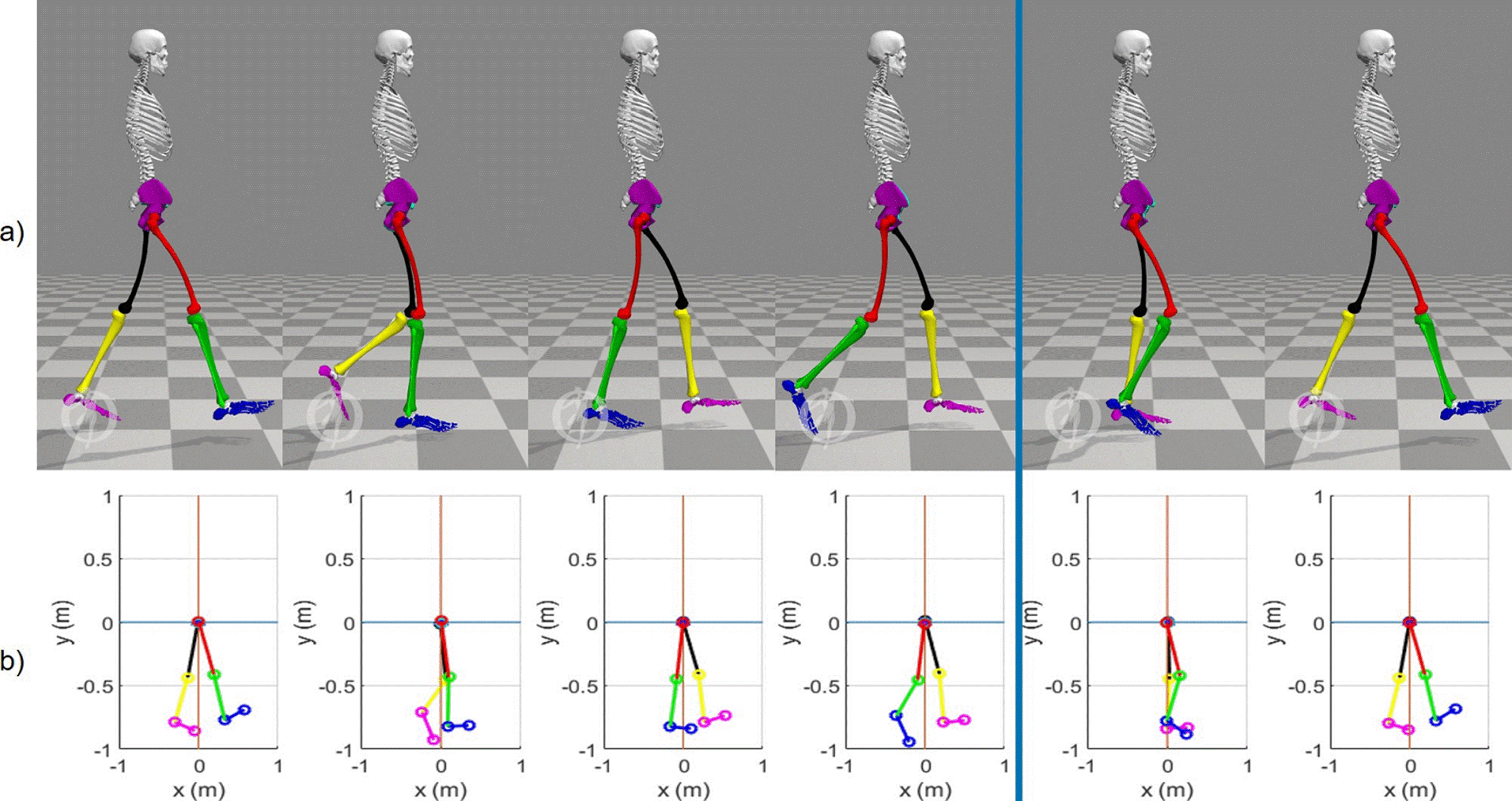
Figure 5 View in the sagittal plane of 6 states of the kinematics of the lower limbs in (0, 20, 40, 60, 80 y 100) % of the normal gait cycle. a) Biomechanical simulation platform [24] and b) Quaternions-algebra based platform.
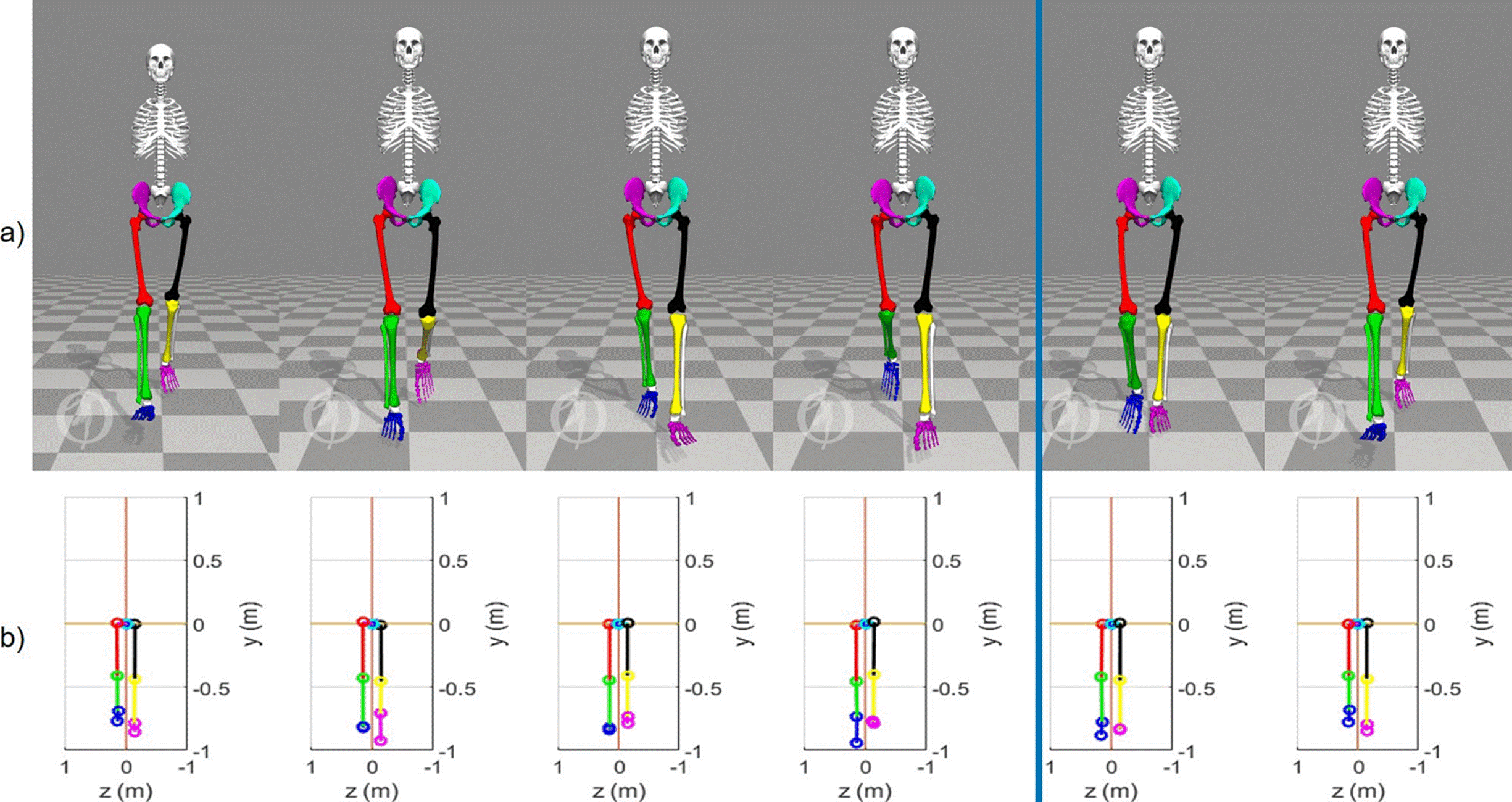
Figure 6 View in the frontal plane of 6 states of the kinematics of the lower limbs in (0,20,40,60,80 y 100) % of the normal gait cycle. a) Biomechanical simulation platform [24] and b) Quaternions-algebra based platform.
For the computational implementation in our approach the base frame Σ0 is considered in an absolute way, that is, the translational movement of the pelvis has not been considered. The blue vertical line in (Figures 5, 6 and 7) indicates the end of the stance phase (60% of the cycle) and the beginning of the swing phase (40% of the cycle).
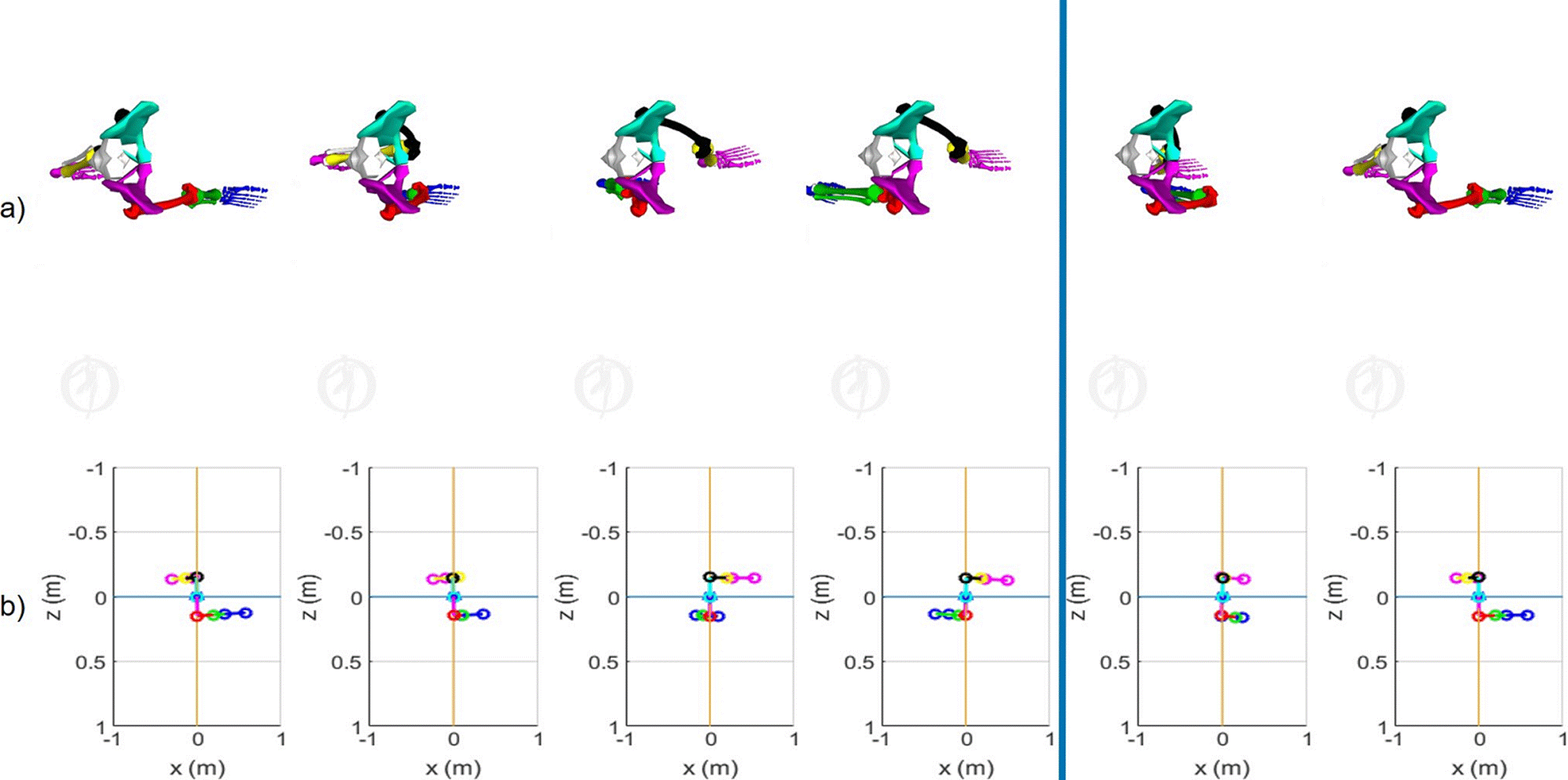
Figure 7 View in the transverse plane of 6 states of the kinematics of the lower limbs in (0,20,40,60,80 y 100) % of the normal gait cycle. a) Biomechanical simulation platform [24] and b) Quaternions-algebra based platform.
In the 3 figures, the gait pattern generated by the mathematical quaternion-based model is similar to the OpenSim® biomechanical model [24], which is very important, since a more practical and less complex implementation can be done with the method based on quaternions than with the D-H convention. Furthermore, as it can be seen, it is possible to approximate the gait pattern of a 23 DoF model [24], with an 8 DoF model like the one proposed in this work, which implies the reduction of orthonormal frames and with it, the instrumentation required for the measurement joint variables are also simplified. In addition to the above, it is possible to model the lower extremities as an analytically open serial chain with quaternion algebra and simplify the fact of modeling each joint independently.
The most widely analyzed joints in the literature are the hip, knee and ankle. In crouched gaits, dorsiflexion and plantarflexion of the ankle are pronounced, on average more than 15° from normal gait. The crouch pattern is generally a problem presented by people with cerebral palsy [30] [31], as well as spastic diplegia and quadriplegia [32] [33]. Disability as a result of a cerebrovascular accident or other types of accident has an evolution that dominates from the stroke phase, immediately after the accident, to a phase of low to severe spasticity, due to the inattention of the patient in tasks of rehabilitation. The diseases are the same, the level of progress that makes the disease critical, changes over time to worsen or improve. Therefore, the analysis of the variation of the angular amplitude, maximum and minimum points of occurrence and shape factor of the angles of the joints is extremely important to determine the evolution of a patient in conditions of disability.
In addition to the joint and geometric parameters of the lower limbs, the calculation of the forward kinematics of position of the hip, knee, ankle and big toe of the right (Figure 8) and left (Figure 9) lower limbs is very important for gait analysis.
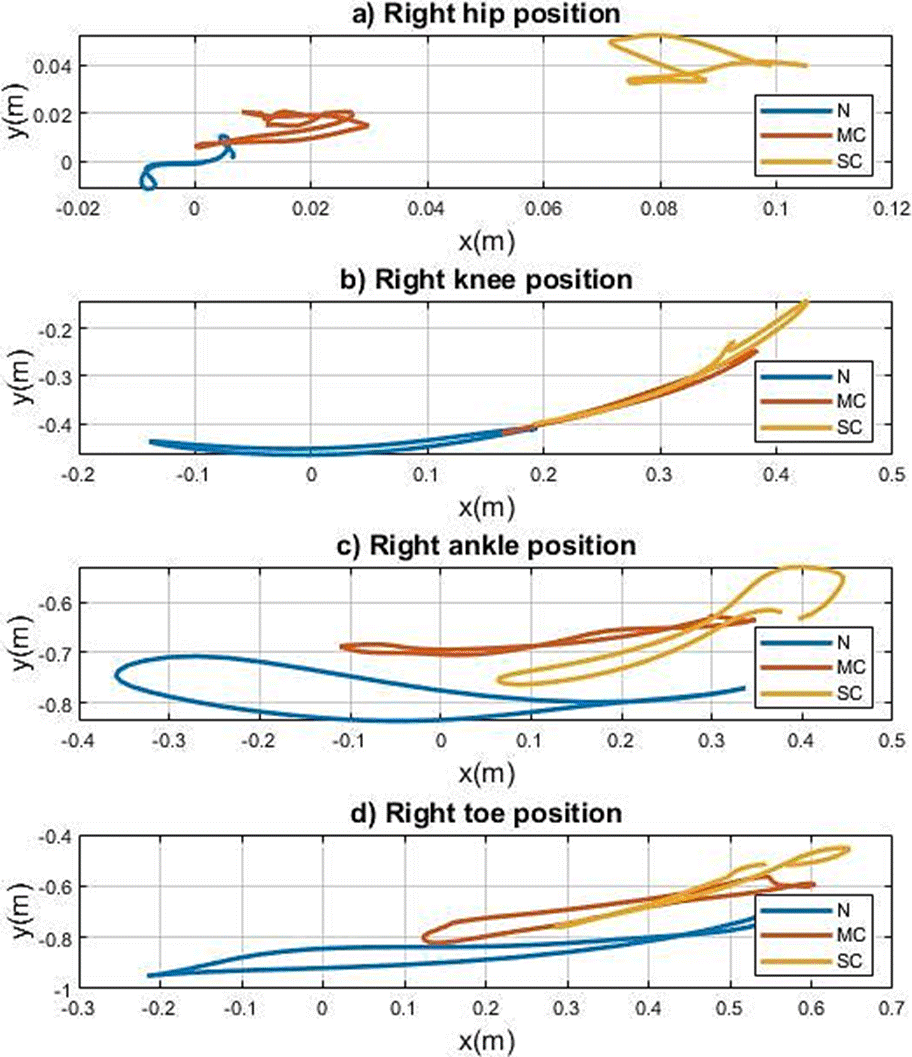
Figure 8 a) Hip, b) Knee, c) Ankle and d) Big toe, right positions in the sagittal plane during gaits: normal (N), mild crouch (MC) and severe crouch (SC), using the quaternion-based approach.
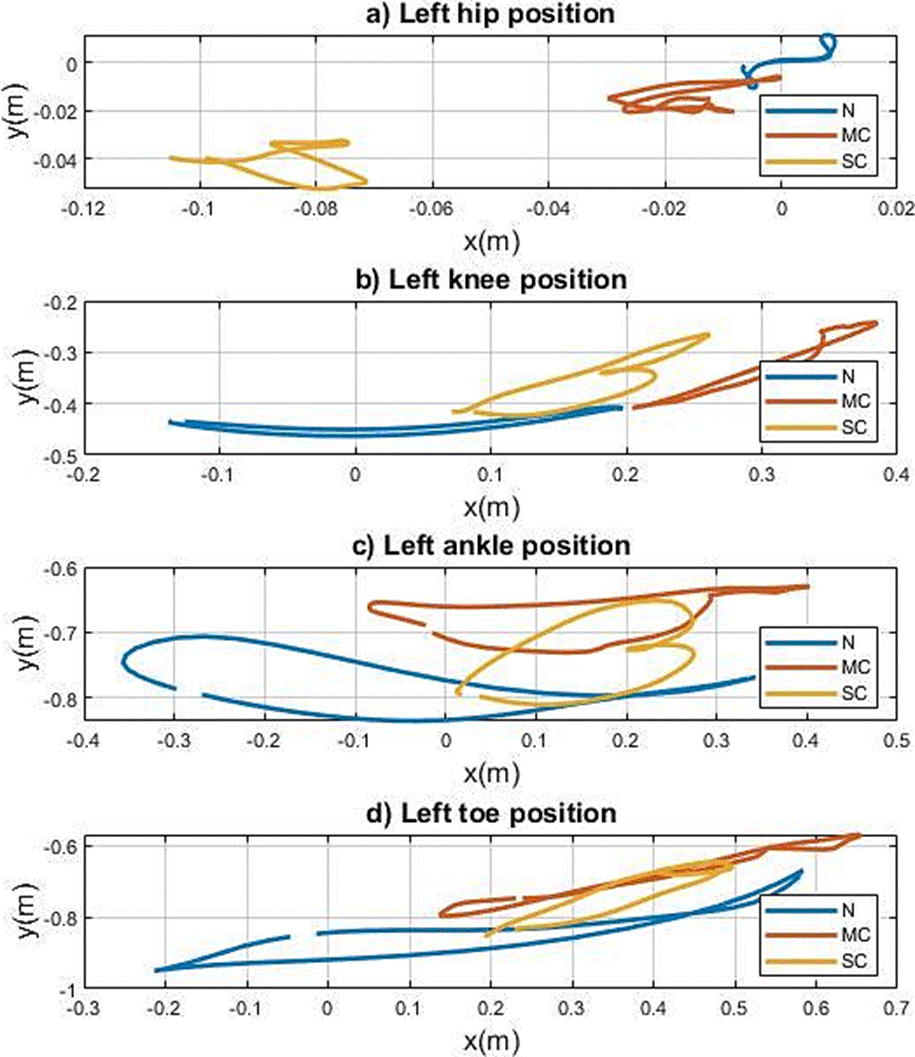
Figure 9 a) Hip, b) Knee, c) Ankle and d) Big toe, left positions in the sagittal plane during gaits: normal (N), mild crouch (MC) and severe crouch (SC), using the quaternion-based approach.
In (Figure 8) and (Figure 9), the positions of the reference frames of the hip, knee, ankle and big toe in the sagittal plane for each limb, respectively, provide information on the behavior in the operational space of the gait. It is possible through these graphs to determine the differences between a normal gait and pathological gaits in relation to the range of motion and shape factor. Which is very useful in the clinical diagnosis and in the treatments related to gait problems.
In (Figure 8a), regarding the positions of the hip frames, it is observed that for a normal gait, both the right and the left move around the origin (z axis), while in the abnormal gaits the centers of position shift .02 m, and 08m for mild crouch and severe crouch, respectively. In addition to highlighting the shape pattern, which makes evident a flexion in the hip for abnormal gaits. The joints have the same shape pattern for the 3 types of gait and only a decrease in movement of approximately 40% is observed. However, the same does not occur for the left limb, since the movement factor is far between normal gait and abnormal gait, in which the severity of gait increases, thereby decreasing the movement in the operational space.
Conventional methods establish a gait analysis from the comparison of the gait pattern associated with each bone structure in its corresponding anatomical plane with the performance of the studied subject. This activity represents exhaustive work to establish a diagnosis, particularly when the performance of one bone structure depends on some other (in the same lower extremity or the other). However, analyzing performance globally significantly reduces analysis time, particularly when running in operational space or gait space; thus, being possible to evaluate classical metrics, and other proposals that better describe the anomaly.
The position of the joints is useful to improve the anatomical models or attachments that help to walk. Likewise, obtaining the position by forward kinematics, the cadence can be obtained from the calculation of the angular velocity, which cannot be obtained from the joint space. Also, through forward kinematics it is possible to obtain the distance between the joints during the gait cycle and from there determine the dependency that exists between them. Therefore, using metrics such as these, through these comparative metrics, it is possible to contribute to diagnosis and decision-making.
The use of specific metrics to develop the biomechanical analysis of gait depends on the objective of interest. Generally, these metrics are used to determine age, gender, pathologies [34] or physiotherapeutic progress [35].
The most common metrics used in gait analysis are speed, cadence, stride length, toe angle, number of daily steps [23]. There are some less used ones based on the calculation of the area of the silhouette to determine gender [36]. This represents an area of opportunity to study and propose new metrics evaluated in the operational space. While the Euclidean distance is the usual norm used in cartesian space, for human gait analysis, it has not been reported as a useful metric. The Euclidean distance between orthonormal frames of the joint references (Figure 3) of lower limbs is shown in (Figure 10) and is calculated as
for the distance between the knees, while
and
are used to calculate the euclidian distance between ankles and big toes, respectively.
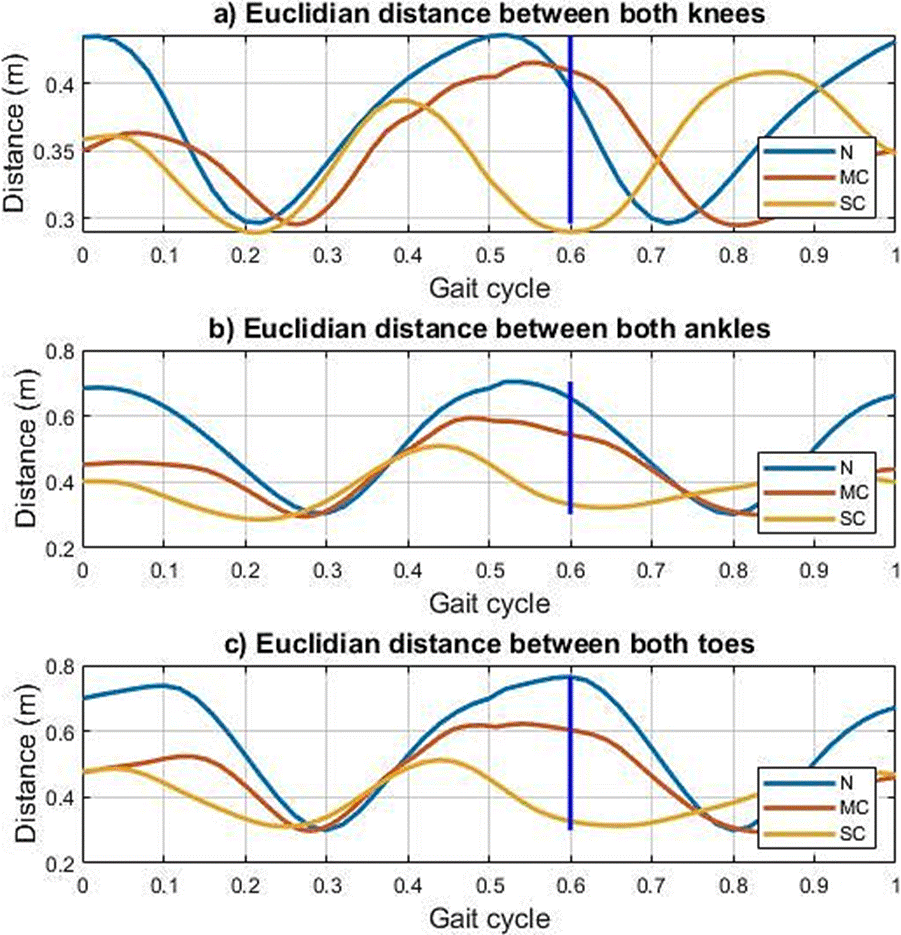
Figure 10 Euclidean distance between a) knees, b) ankles, and c) big toes of the lower limbs during normal (N), mild crouch (MC) and severe crouch gaits.
The use of the metric of the Euclidean distance in the cartesian space of the gait allows to establish a distance pattern to determine the normal and abnormal parameters during the evaluation and it is related to the range of motion of each joint. The distance between the right and left hip references due to the human model used is kept constant and for this reason is not presented in (Figure 10). The distance between knees references during normal gait is greater for each gait sample than mild and severe crouch gaits, which implies that the global performance in abnormal gaits reflects a limitation of movement, which is characteristic of diseases such as cerebral palsy or hemiplegia. On the other hand, the form factor of the distance measurement of normal gait references can be established as the gait pattern in cartesian space, so it is clear that in (Figure 10a) the abnormal gaits do not maintain the same distance between knees as the pattern. Similar performance in measuring the Euclidean distance between the ankles and the big toes of both lower limbs.
CONCLUSIONS
Unlike classical Denavit-Hartenberg and geometric methods for calculating the forward kinematics of position of a serial kinematic chain, the method based on quaternion algebra proposed in this work reduces the complexity of kinematic modeling and the computational cost of numerical calculation when the number of degrees of freedom of the chain increases. Furthermore, through the method introduced, it is possible to approximate the gait pattern of the 23 DoF human model, through the 8 DoF model used in this work, reducing the number of orthonormal frames in the modeling and instrumentation required for the acquisition of biomechanical data of the gait.
The analysis in the 3 anatomical planes of the 8 DoF model allows an evaluation of the performance of the lower limb joints during the gait cycle both, independently and as a whole. If the movements of the joints in a single anatomical plane are evaluated, as for example in the 3 DoF model presented, a local analysis is obtained, which does not consider the movements in other anatomical planes that limit the comprehensive diagnosis, and there may be loss of an objective diagnosis.
Finally, gait analysis in the cartesian space from the joint space is useful to assess gait abnormalities of the studied subject with respect to the normal gait pattern. The evaluation in the operational space of abnormal gaits, such as mild crouch and severe crouch respect to normal gait, shows an anatomical displacement of excessive flexion in the knees and ankles presented in this type of gait, noted numerically through the proposed model. In addition, it is possible to determine the normal patterns and metrics of these and other joints such as the hip, which help diagnose diseases related to the detected abnormalities. The use of other metrics in cartesian space, the calculation of inverse kinematics, and differential kinematics can greatly improve the biomechanical gait analysis.











 nueva página del texto (beta)
nueva página del texto (beta)


