INTRODUCTION
In neurons, maintaining the homeostasis of calcium ions (Ca2+) is essential for proper signaling and function. The endoplasmic reticulum (ER) serves as the main Ca2+ storage organelle in neurons and has mechanisms of influx and efflux of this ion. Such mechanisms, located on the ER membrane, help to regulate the cytosolic concentration of Ca2+. The influx mechanism is based on Ca2+ pumps, while the most important efflux mechanisms are triggered by inositol 1,4,5-trisphosphate (IP3) receptors (IP3-Rs) and ryanodine receptors (RyRs). The rise in the level of Ca2+ in the cytosol active the large-conductance calcium-activated potassium channels, or big potassium (BK) channels.
Various mathematical models have been developed to replicate the release of Ca2+ from the ER and the pattern of the cytosolic Ca2+ concentration, hereafter denominated [Ca2+]cyt. However, they have not been associated with BK channels in order to research their joint function at the somatic level, explore the mechanisms involved, and determine the importance they have in neuronal activity. A theoretical study was carried out on the functional coupling of IP3-Rs to BK channels in a single neuron and the effects produced. An interaction is proposed in the soma of the neuron in a microdomain formed by the proximity of the BK channels of the plasma membrane to the calcium efflux channels triggered by the IP3-Rs located on the ER membrane.
BK channels
Large conductance (BK) channels are part of the family of calcium-activated potassium channels. They are distinguished from other calcium-activated potassium channels (small and intermediate conductance) by their capacity to couple [Ca2+]cyt and sense the membrane potential variations. BK channels are widespread in the brain, being found in the cerebral cortices, cerebellar cortex, hippocampus, olfactory bulb, vestibular nuclei, basal ganglia, hypothalamus, and thalamus [1].
Calcium-activated potassium channels exist in diverse cell types [2]. On neurons, BK channels are present in dendrites, soma, axons, and synaptic terminals [1]. Upon analyzing aplysia nerve cells, Meech [3] identified for the first time a potassium current activated by a rise in the level of [Ca2+]cyt. After microinjection of calcium, the cell membrane was hyperpolarized and an increase in Ca2+-activated K+ conductance (gKCa) occurred concomitantly [3]. Since then, these channels have been investigated to characterize their molecular structure, electrophysiology, and pharmacology [4]. According to their single-channel conductance, KCa channels are divided into three main subfamilies: (1) small conductance (SK) (4-14 pS), (2) intermediate conductance (IK) (32-39 pS), and (3) large conductance (BK) (200-300 pS) channels [4] [5].
The BK channels have several distinctive characteristics. (1) They are homotetramers with two regulatory domains containing two high-affinity Ca2+ binding sites. (2) They are voltage and calcium-dependent, requiring both membrane depolarization and calcium for their activation. Ca2+ binding and voltage sensor activation act almost independently to enhance channel opening [6]. BK channels can open in the absence of calcium but are more sensitive to calcium at depolarizing voltage steps [2]. Hence, their sensitivity to calcium is strongly dependent on the membrane potential. The dissociation constant (Kd) for calcium is in the micromolar range at -60 mV and in the nanomolar range at +20 to +40 mV [7]. (3) BK channels are fast activating (on the order of 1 ms or less) compared to IK and SK channels, which have a slow activation time (lasting hundreds of milliseconds or over a second, respectively) [8].
BK channels have various functions in the central nervous system. At the soma of many neuronal cells, they control the speed of action potential repolarization and mediate the rapidity of afterhyperpolarization. Therefore, they can influence spike frequency adaptation [9] [10]. They are often physically associated with voltage-gated calcium channels (VGCCs), thus forming microdomains with them [11] [12]. Due to their presence in nerve terminals and their co-assembly with VGCCs at active zones, BK channels are particularly suitable for regulating the release of neurotransmitters, increase the duration of PA, prevent backpropagation in dendrites, and produce a decrease in firing frequency [9] [13] [14].
The concentration of free and bound [Ca2+]cyt is reported to be approximately 100 nM and 10 μM, respectively [15]. While a localized increase in [Ca2+]cyt has been evidenced in some studies, others show spatio-temporal calcium signaling restricted to nano and microdomains in neurons [16] and smooth muscle [17] [18]. In a BK channel-VGCC microdomain, according to Fakler and Adelman [18], the kinetics of [Ca2+]cyt exhibit a localized boost of up to 20 μM in neurons. The [Ca2+] cyt concentration decreases with distance due to the diffusion process and interaction with the chelators (1,2-bis(o-aminophenoxy)ethane-N,N,N',N'tetraacetic acid (BAPTA) and ethylene glycol-bis(b-aminoethyl ether)- N,N,N',N'-tetraacetic acid (EGTA) [18].
Endoplasmic reticulum (ER)
Because of containing a high concentration of Ca2+ binding proteins, the ER is the main Ca2+ storage organelle in cells. Indeed, the total amount of Ca2+ may be >1 mM, while the concentration of free [Ca2+]ER (Ca2+ in the ER) has been quantified at 100-700 μM [19].
To maintain equilibrium, mechanisms of influx and efflux of Ca2+ are activated on the ER membrane. There are two types of processes related to the efflux of Ca2+ from the ER, being the Ca2+-induced Ca2+ release (CICR) and IP3-induced Ca2+ release (IICR) processes. The [Ca2+]cyt interacts with ryanodine receptors and IP3 receptors (RyRs, IP3-Rs) in the former and IP3 with its receptors (IP3-Rs) in the latter, in both cases to release Ca2+ from the ER [20]. On the other hand, Ca2+ is recaptured into the ER by the activity of smooth endoplasmic reticulum Ca2+-ATPase (SERCA) pumps [21]. Thus, a low concentration of [Ca2+]cyt (50 - 100 nM) is maintained by the coordinated action of the inflow of Ca2+ to the ER through pumps on the ER membrane, and the efflux of Ca2+ from the cytosol to the extracellular space through pumps (PMCA) on the plasma membrane [22].
BK channel - IP3 receptor interaction
The BK channel/IP3-R microdomain has received less attention, and its role is controversial. IP3-Rs are localized in the ER membrane and the BK channels in the plasma membrane. The BK channels and IP3 receptors are very close to one another [23]. The ER membrane is believed to be initially generated as part of the nuclear envelope, which then expands and morphs into a complex reticulum that can extend to distant cellular compartments such as the axons, dendrites, and dendritic spines of neurons, but with a similar morphology and there is closeness between the ER membrane and the cytoplasmatic membrane [24] [25] [26]. The cisternae of the ER are classified in accordance with their proximity to the plasma membrane. Type I is the farthest from the plasma membrane, while type II and III are nearer, frequently following its profile [26].
Pan et al., reported the interaction between BK channels and IP3-Rs in human embryonic kidney cells (HEK293) [27]. Neuropeptide galanin activates galanin receptors (GalR2s), and IP3-Rs are activated through the protein kinase G pathway. The increase in [Ca2+]cyt is due to Ca2+ efflux from the ER through IP3-Rs. The authors demonstrated that the rise in the level of [Ca2+]cyt comes from the ER but did not quantify this change.
In arterial smooth muscle cells, relaxation and contraction are regulated by calcium released from the sarcoplasmic reticulum. The flow of calcium from the ER to the cytosol (induced by IP3 and ryanodine) activates the BK channels, thus facilitating a negative feedback mechanism in opposition to vasoconstriction [17]. There is evidence of the proximity of BK channels and calcium release sites. This is further supported by co-immunoprecipitation experiments [28]. As a consequence, such channels would be exposed to a high calcium concentration (>10 μM, in the order of 1-100 μM).
In neurons, Irie and Trussell [23] described a nanodomain between RyRs on the ER membrane and plasma membrane VGCCs (voltage-gated Ca2+ channels), and another one between RyRs and BK channels in the soma of cartwheel inhibitory interneurons of the dorsal cochlear nucleus. Through the VGCC-RyR interaction, the latter receptors trigger the release of Ca2+. The internal increase in calcium acts on plasma membrane BK channels to control action potential activity and shape the burst. The interaction of the nanodomains and the Ca2+ transients must be very rapid (in a millisecond timescale), and thus arise only tens of nanometers from the plasma membrane [23].
IP3 is highly mobile in the cytosol. It is synthesized in the plasma membrane and diffuses into the cell where it encounters its specific receptors (IP3-Rs) on the ER [29]. In neocortical pyramidal neurons, IP3 produces calcium waves via activation of metabotropic glutamate receptors. When measured with non-buffering low-affinity Ca2+ indicators, such waves have a peak amplitude of over 5 μM [30] and propagate with a velocity of ~100 μm/s [31]. According to Ross [31], the release of Ca2+ from ER has been less studied because it is not associated with specific changes in the membrane potential. As can be seen in this work, the impact of the release of Ca2+ from ER on the membrane potential was researched indirectly through the BK channels.
The importance of the interaction between BK channels and voltage-gated calcium channels has been demonstrated in the release of neurotransmitters, where they play a regulatory role that prevents excitotoxicity [32]; in the smooth muscle of blood vessels, where it regulates blood pressure and plays an important role in preventing hypertension [33]. In these cases, the prevention mechanism is a negative feedback system. The experimental study is facilitated because both channels are found on the same membrane, and voltage clamping and transfections can be performed to combine different types of VGCC channels with the BK channel, etc. On the other hand, the experimental study of the BK/IP3-R complex is more difficult, the channels are in different membranes and consequently, voltage clamping cannot be performed. This justifies a theoretical study of the BK/IP3-R. It is unknown whether, at a somatic level in neurons, the BK/IP3-R interaction is present as a protective mechanism. Based on the reported studies, the coexistence of BK and IP3-R channels at the somatic level is known [23] and of the proximity of the cell membrane and the endoplasmic reticulum and contact sites between these structures [24], necessary conditions for the presence of BK/ IP3-R. The proposed hypothesis is that: in neurons, at the somatic level, there is a BK/IP3-R interaction. If this is so, what would its role be in neuronal activity? What would be the mechanisms involved? It is not known whether an abrupt and short-term outflow of Ca2+ could activate BK channels in the neuron’s soma; it is also not known whether there is a commitment between the number of BK channels present in the membrane and the response of the neuron to [Ca2+]cyt.
Modeling of Ca2+ release from IP3R
Based on detailed knowledge of the timescales of Ca2+ release from the ER and the pattern of [Ca2+]cyt concentration, mathematical models have been developed to replicate variations in [Ca2+]cyt. The resulting models are of three types. Firstly, there are models for the release of Ca2+ (with simplified dynamics) from the ER or the sarcoplasmic reticulum through the IP3-R. Such early models are purely phenomenological [34] [35]. Secondly, some models incorporate molecular details of the interaction of IP3 and Ca2+ with the IP3-R, considering microscopic kinetics and a detailed gating scheme for the receptor [36] [37] [38] [39] [40] [41]. Thirdly, some models (e.g., the one created by Blackwell and Kotaleski, in [39]) also incorporate second messengers within the biochemical reactions that are triggered by metabotropic glutamate receptor (mGluR) activation and lead to IP3 production. Each group of models has different timescales.
The mathematical models are related to the molecular interaction of IP3 with the IP3-R and the Ca2+activated channel, which are activated sequentially for the release of Ca2+ from the ER. These models have employed different mathematical techniques [40]. The current contribution focuses on the interaction of [Ca2+]ER with BK channels. Detailed molecular kinetics of the mechanisms of release of Ca2+ from the ER is not essential for the purpose of this work. The phenomenological model of Goldbeter of such Ca2+ release was herein found to be sufficiently accurate and appropriate in its timescale and was combined with the phenomenological model of Hodgkin and Huxley. The latter formulation describes the electrical activity of neurons [41]. Based on the aforementioned models, the present study theoretically explored the function of a BK/IP3-R microdomain.
MATERIALS AND METHODS
In the development of a new model, consideration was given to the spatial structure of the soma and some key concepts related to the kinetics of Ca2+. The increase in Ca2+ is located in the microdomain [16] formed mainly by the following factors [28]: the BK channels on the soma membrane [1] [44] and the Ca2+- and IP3-R-sensitive channels on the ER membrane [42]. The two membranes are very close to one another [26]. There is evidence from electron microscopy, with 3D reconstructions, of the proximity of the plasmatic membrane with the ER membrane and of numerous contact sites between these structures, mainly in the neuron soma [24].
The Hodgkin and Huxley formalism and the BK model
The electrical activity of the neuron was reproduced with the Hodgkin and Huxley formalism (H-H model), consisting of an equation that represents the membrane potential (Equation 1) and others that define channel gating variables (Equations 2-5) [45] [46].
Where αm(V), βm(V), αh(V), βh(V), αn(V), βn(V), αq(V), and βq(V) are activation and inactivation gatin variables and are defined according to the following empirical equations (Equations 6-13) [45] [46] [47]:
Table 1 The parameters of the H-H model (from [45]).
| Symbol | Values | Units | Definitions |
|---|---|---|---|
| V | -90* | mV | Membrane potential |
| Cm | 1 | µF·cm-2 | Membrane capacitance |
| ENa | 50 | mV | Equilibrium potential for Na+, K+, and leak |
| EK | -77 | ||
| EL | -22 | ||
| ḡNa | 120 | mS·cm-2 | Maximum conductance for Na+, K+, leak and BK |
| ḡK | 20 | ||
| ḡL | 0.3 | ||
| ḡBK | ** | ||
| [Ca2+]cyt | *** | µM | Calcium ions in the cytosol |
*Initial condition
**Input into the simulator
***Is taken from the Goldbeter model
Goldbeter Model
The mathematical model of Goldbeter (1990) was found to be adequate [32] because the time involved in the BK channel is on a millisecond scale [48] [49] [50] and our interest is in the [Ca2+]cyt concentration and not in the details of the interaction of IP3 with IP3-R. Hence, two different mechanisms were contemplated for the release of Ca2+ from the ER, one sensitive to IP3 (the IICR) [38], and the other to Ca2+ (the CICR) [48].
Dupont and Goldbeter developed another model with a single compartment. In a single group, considering the existence of the same two types of channels (one sensitive to Ca2+ and the other to IP3), no oscillations occur unless the contribution of the IICR is insignificant compared to that of the CICR [49]. Oscillations in [Ca2+]cyt are similar in the one- and two-compartment models [49]. The latter was employed in the present study since it does not require such an extreme decrease in the contribution of the IICR as needed in the one-compartment model.
The model has two variables, free [Ca2+]cyt (Z) and free [Ca2+]ER concentrations, modulated through the Ca2+ -sensitive mechanism (Y). The system is governed by the two kinetic equations [32]:
Where V0 is related to the flow of Ca2+ into the cell, k to its flow out of the cell, V1 to its flow into the cytosol from the IP3-sensitive mechanism, β to the saturation function of IP3-Rs (cooperative nature), and Kf to the leaky transport of Y into Z. Finally, V2 expresses the rate of the SERCA pump and V3 the rate of transport of Ca2+ released from the IP3-sensitive mechanism into the cytosol.
VM2 denotes the maximum rate at which Ca2+ is pumped into the ER store and VM3 the IP3-sensitive release of ions from this location. The complementary processes are represented by Hill functions. Thus, nHill and mHill depict the cooperativity coefficients, pHill reflects the degree of cooperativity of activation, and the constants K2, KR, and KA designate the point at which pumping, release, and activation are triggered [49]. Since the ATPase pump (SERCA) binds to two calcium ions per molecule of ATP, its activity is expressed by using Michaelis-Menten kinetics and a value of 2 for the Hill coefficient (Equation 16) [50].
Table 2 Parameters of the Goldbeter model [32].
| Symbol | Values | Units | Definitions |
|---|---|---|---|
| Rate of transport from Ca2+ -sensitive pool into the cytosol | |||
| V3 | flow rate of Ca2+ from the ER to the cytosol | ||
| VM3 | 500 | µM/s | maximum V3 |
| KR | 2 | µM | constants |
| KA | .09 | µM | |
| kf | 1 | 1/s | rate constant (Ca2+ leak) |
| ATP-driven pumping of Ca2+ from the cytosol into the Ca2+ -sensitive pool | |||
| V2 | pumping rate of Ca2+ into the ER (by SERCA) | ||
| VM2 | 65 | µM/s | maximum V2 |
| K2 | 1 | µM | constants |
| Efflux of Ca2+ out of the cell (PMCA bomb) | |||
| K | 10 | 1/s | rate constant |
| Hill coefficients | |||
| nHill | 2 | Hill coefficient (SERCA bomb) | |
| mHill | 2 | Hill coefficients Ca2+
release from Ca2+ -sensitive poll |
|
| pHill | 4 | ||
The system of equations was solved simultaneously by the numerical method with a fourth-order RungeKutta algorithm (dt = 0.01) written on Visual Basic [53] [54]. The initial conditions were V= -90 mV, and [Ca2+] cyt= 0.1 μM (value entered in the simulator). The simulator was developed and compiled to use in the Windows® environment.
RESULTS AND DISCUSSION
The module for inputting data into the simulator (Figure 1) provides an interactive resource for experimental recordings, allowing for access to all the parameters of the Goldbeter model [49]. There are three types of variables: those that increase or decrease [Ca2+]cyt, as well as the ones related to the degree of cooperativity of the activation process (nHill, mHill, and pHill).
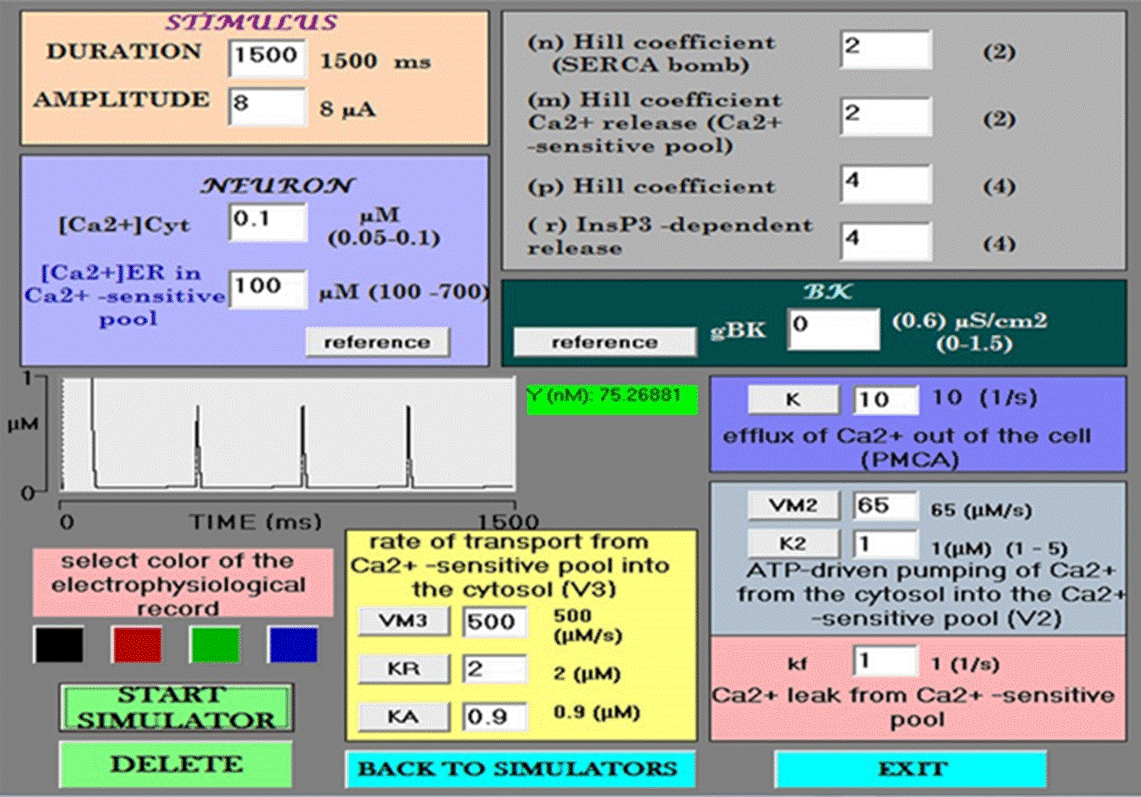
Figure 1 Data entry module. The simulator begins at default values for each variable. An enlargement of the small Ca2+ spikes is shown in the center (amplitude = 763 nM). Under such conditions, the control neuron does not have BK channels (gBK= 0).
Firstly, the influx of Ca2+ to the cytosol depends on the rate of transport through the IP3-sensitive mechanism (r= V1*β) and the Ca2+-sensitive mechanism (V3), the maximum rate of Ca2+ pumping release from the ER store (VM3), the threshold constants for release and activation (KR and KA, respectively) (Figures 1 and 5), and the passive leak (kf). Secondly, the efflux of Ca2+ out of the cytosol depends on the outflow of Ca2+ from the cell (k) (due to the PMCA pump), the inflow rate of Ca2+ into the ER from the cytosol, involving the rate and maximum rate of the SERCA pump (V2 and VM2), and the threshold constant for the latter pumping action (K2) (Figures 1 and 7). Thirdly, variables must consider the cooperativity degree of the activation process. The range of values for free [Ca2+]cyt is 0.05 to 0.1, and that for free [Ca2+]ER is 100 to 700 μM [53].
When opening the simulator, the default values for each variable appear. The BK channel conductance value starts at zero. The value of free [Ca2+]cyt and free [Ca2+]ER are 0.1 and 100 to 700 μM, respectively. Each simulation was carried out with the current clamp protocol. To match the timescales of the ion channels in the model with those of the Goldbeter model, a long depolarizing current pulse (1.5 s) is used. Upon starting a simulation under these conditions, the recorded action potentials correspond to the Hodgkin and Huxley model with only voltage-dependent Na+ and K+ channels. The parameters of the Goldbeter model leading to oscillations in Ca2+ begin at the reference values, and immediately after there is an increase in [Ca2+]cyt of 5 μM with a duration of 96 ms, (a local [Ca2+] cyt transient) followed by calcium spikes of 741 nM (Figure 2).
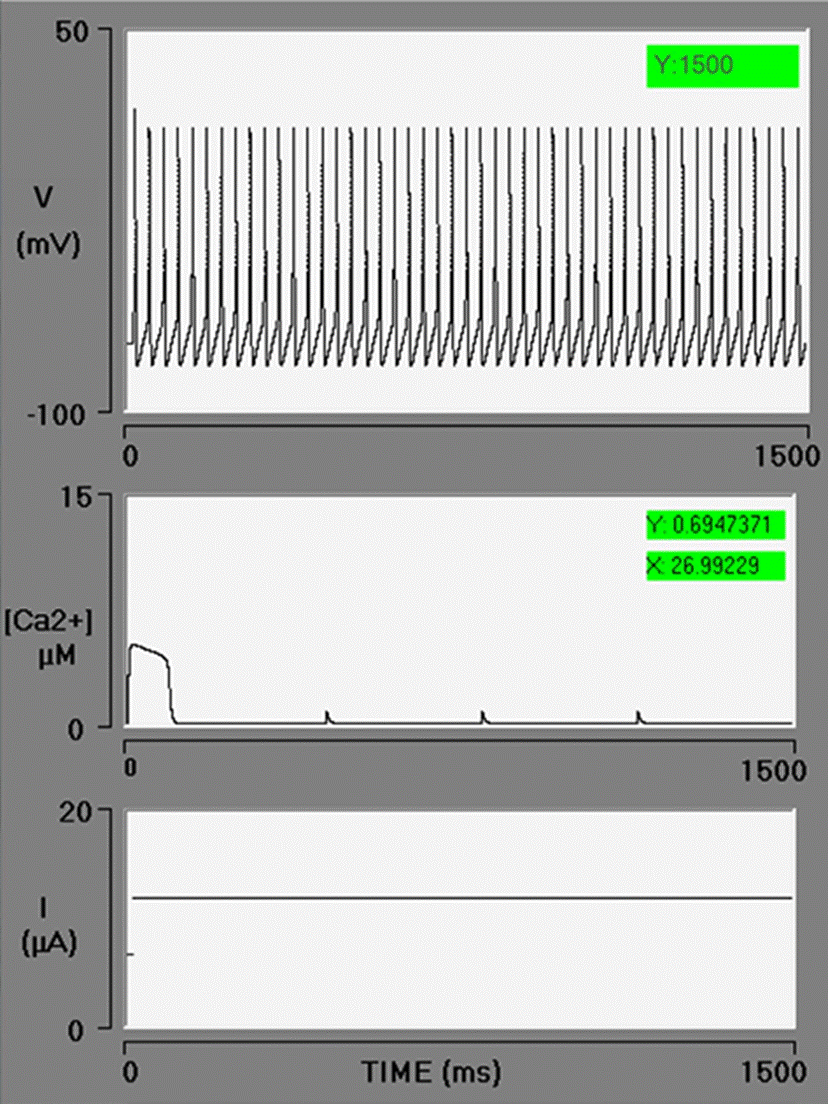
Figure 2 Electrophysiology interface simulator with three oscilloscope screens. In the control simulation, the spike train generated by the Hodgkin and Huxley model is displayed on the upper screen. The local cytosolic Ca2+ transient followed by three Ca2+ spikes is exhibited on the middle screen. The stimulus current pulse (with a duration of 1500 ms) is illustrated on the bottom screen. In this simulation, the BK conductance is zero.
Khodakhah and Ogden [54] reported that IP3 triggers a release of Ca2+ from the ER with an initial well-defined delay, which decreases as the concentration of IP3 rises (mean, 85 ms at 10 μM IP3). In the present study, the simulation is initiated at the moment Ca2+ is released from the ER. Hence, a series of factors are not considered in the model: the interaction of the first messenger with the receptor on the plasma membrane, the cascade of second messengers, the explicit interaction of IP3 and Ca2+ with IP3-Rs, and the corresponding delay in the release of Ca2+. The dynamics of Ca2+ is local. The diffusion and chelation of Ca2+ are not simulated.
Diverse physiological processes (including pathological phenomena) are modulated by the generation and propagation of [Ca2+]cyt signals. The release of Ca2+ from the ER takes place through sparklets, sparks, blink, scintilla, puffs, and other forms [16]. Since such elementary events are produced in microdomains, the multiple forms of Ca2+ release confer intracellular Ca2+ signaling with a broad architecture in space, time, and intensity, which in turn underlies signaling efficiency, stability, specificity, and diversity [55]. The calcium buffers are instrumental in achieving temporal, spatial, and functional compartmentalization under these conditions, creating steep gradients in a close proximity of channels, until reaching an internal calcium concentration on the order of tens of micromoles [56]. The local [Ca2+]cyt transient in this simulation corresponds to a Ca2+ spark, characterized by Cheng and Lederer as having an approximate amplitude of 5 μM and a duration of 35 milliseconds in a space of 30 nm [55]. Under the current conditions, the duration of the spark is three times longer and a space of 90-100 nm would be expected. The activation of BK channels by spark coming from the ER has been described in smooth muscle [17] but not in neuronal cell bodies. The microdomains of Ca2+ consist of very small spaces (nm) between structures (e.g., voltage-gated Ca2+ channels and BK channels or IP3-Rs), thus involving very local increases in Ca2+ [57]. Microdomains between BK channels and IP3-Rs have been found in different cells, including neurons, with distances of 100 nm or less [23] [59].
Figure 3 presents four simulations with the following values of Ca2+ in the endoplasmic reticulum pool: 100, 300, 600, and 700 μM. As a consequence, there is an increase in amplitude (5, 7, 10, and 11 μM) and duration (96, 235, 389, and 431 ms), respectively, of [Ca2+]cyt.
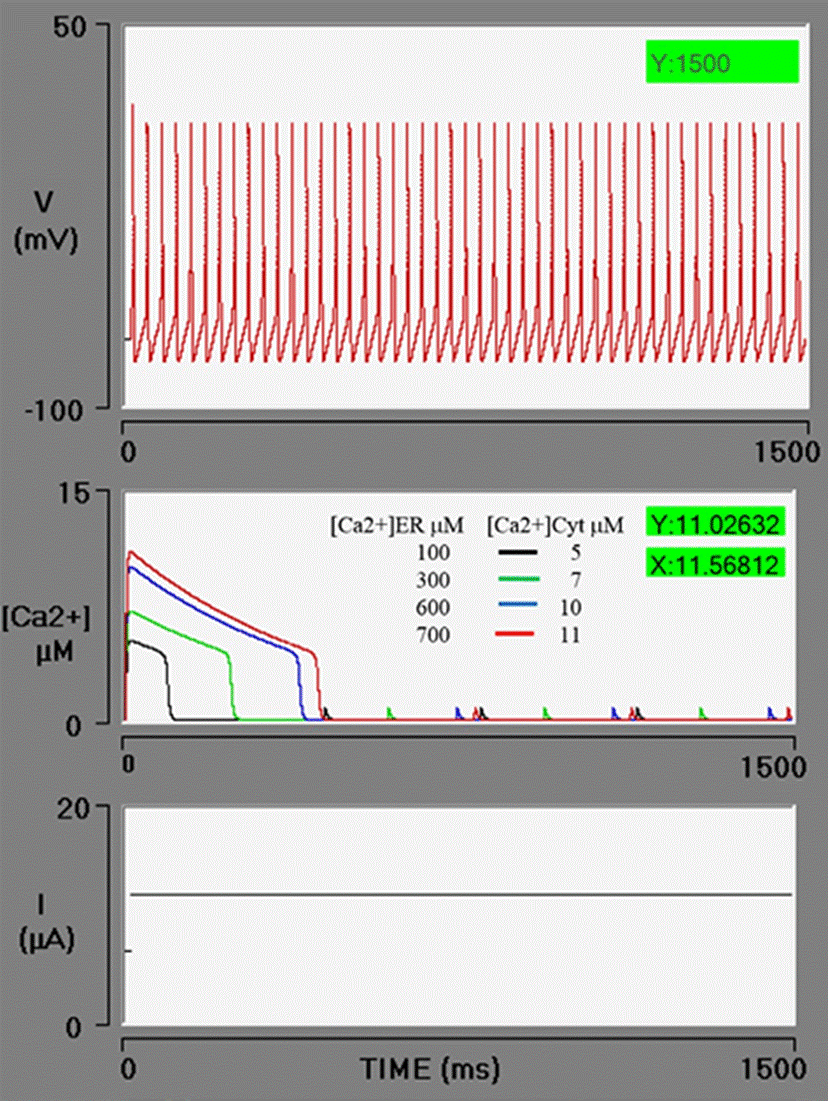
Figure 3 Simulations of the effect of an increasing concentration of free [Ca2+]ER (Ca2+ in the endoplasmic reticulum) on the level of free [Ca2+]cyt (Ca2+ in the cytosol). When the simulations have an [Ca2+]ER value of 100, 300, 600, or 700 μM (red box), curves the calcium (sparks) are generated on the middle oscilloscope screen in black, green, blue, and red, with an amplitude or 5, 7, 10 and 11 μM, respectively. The PA train is unaffected because the neuron does not have BK channels (gBK = 0).
The level of [Ca2+]cyt rises in function of the difference in concentration between free [Ca2+]cyt and the free [Ca2+]ER, quantified with the Hodgkin and Huxley formalism (Equation 18).
Where V3 is the IP3-sensitive Ca2+ efflux out of the ER through its membrane and into the cytosol, VM3 denotes the maximum rate of such Ca2+ release, and R[Ca2+] depicts the fraction of the calcium channels in the open state, which depends on the [Ca2+]cyt concentration. The function R has been described by the same sort of mathematical formulations as for the opening of voltage-gated channels, in most cases either by Markov kinetic schemes or by Hodgkin-Huxley-style gating particles. The Goldbeter model uses a simpler approach with a suitable Hill coefficient, nHill (Equation 17) [32].
Interaction of IP3-R/[Ca2+]cyt/BK channels
The opening of BK channels is governed by membrane depolarization and a rise in the concentration of [Ca2+]cyt. Figure 4, shows the effect of a 5 μM increment in [Ca2+]cyt on the action potential train in the presence of the BK channel. Each simulation has 100 μM of [Ca2+]ER, with all variables set at the previously described initial values. A range was established for the BK channel conductance values, generally considered as 0.1 μS/cm2 in hippocampal neurons and 1.2 μS/ cm2 in sympathetic ganglion cells, in agreement with the values proposed by Traub and Miles and by Koch and Segev, respectively [46] [60]. Four simulations were carried out with a BK conductance of 0.1, 0.6, 1.2, and 1.5 μS/cm2, affording the following results (respectively): no effect on the PA train (1500 ms), braking of the PA train at 1050 ms, fast braking at 83 ms, and braking immediately after the first action potential (values in green boxes in Figure 4 A, B, C, and D). Hence, there was a conductance-dependent effect of the [Ca2+]cyt: the higher the conductance, the greater the effect of the [Ca2+]cyt concentration.
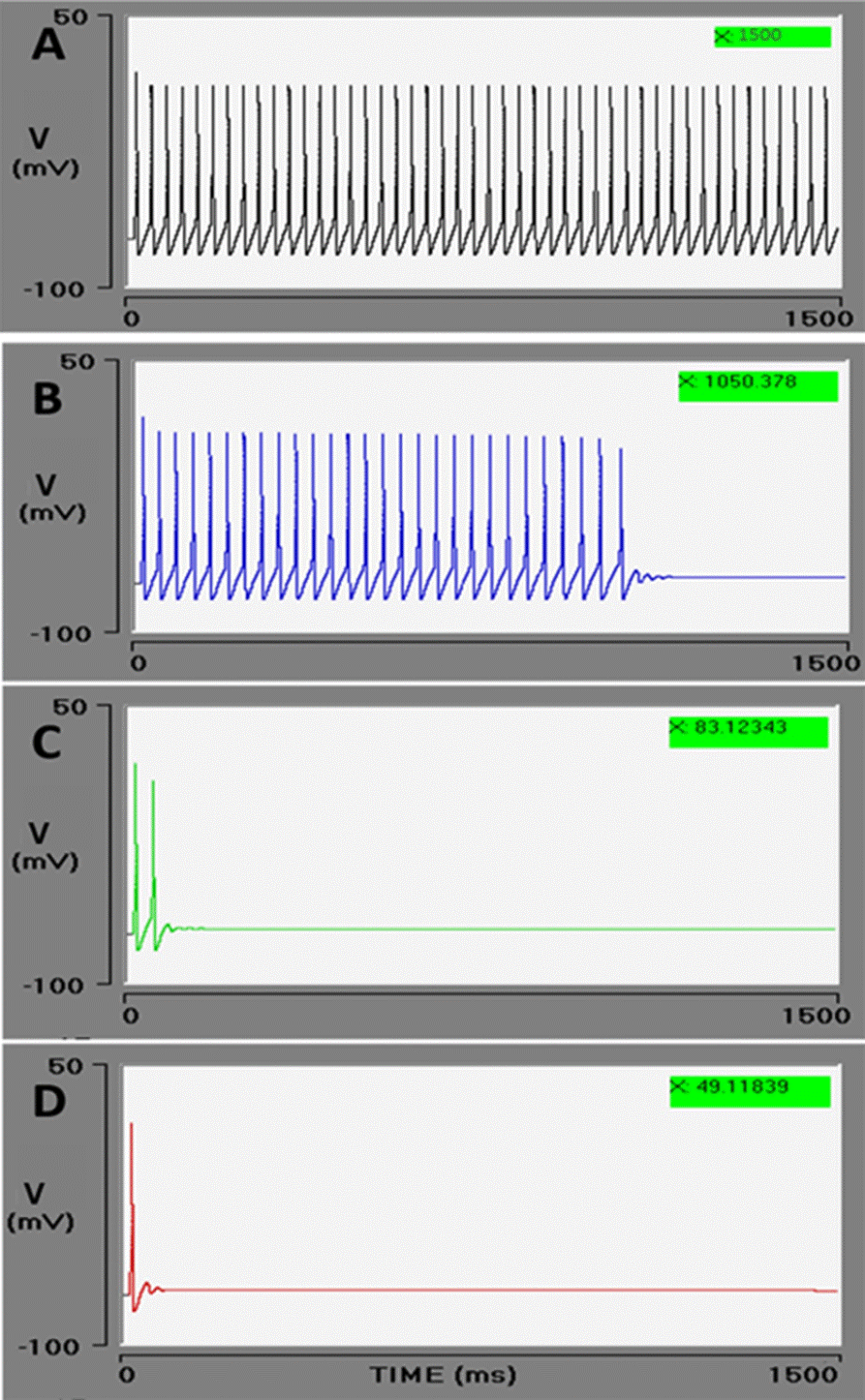
Figure 4 Effect of BK conductance on the action potential train. The Goldbeter model produces a 5 μM increment in cytosolic calcium. In these conditions, increasingly rapid braking of the action potential train is observed during the interaction of the BK channel with cytosolic calcium. As the conductance of BK channel (gBK) is intensified (μS/cm2): 0.1 (A), 0.6 (B), 1.2 (C), and 1.5 (D), the PA train durations decreases: 1500, 1050, 83, and 49 (ms), respectively (green boxes). The effect is to stop the action potential train.
The dependence of the BK channel on the voltage is of an allosteric type. It has been proposed that the increase in [Ca2+]cyt could occur almost simultaneously with a rise in voltage, as long as the calcium source is close, as in the case of the BK/VGCC complex [60]. In the present study, a BK/IP3-R complex is assumed. Each stimulus (voltage and Ca2+) interacts with different parts of the channel [7]. The overall conductance of BK channels on the plasma membrane is determined by the conductance of each channel as well as the number and open state probability of these channels (Equation 19) [61].
Where nc denotes the number of ion channels, ĝ represents single-channel conductance (200 to 300 pS), and Po is the open state probability value (0 to 1).
The activation of BK channels by a rise in [Ca2+]cyt results in a greater open state probability and an enhanced K+ efflux. This is the molecular kinetics of channel opening induced by Ca2+ and voltage. The [Ca2+] cyt concentration continues to be optimal for a greater channel opening until the saturation point is reached. Consequently, the conductance for each cell depends on the number of channels, and the unit conductance of each one. The results of the simulation indicate that the ease of response of the neuron to the concentration of Ca2+ depends on the number of BK channels present in its membrane. The higher the conductance, the higher the response to Ca2+ and vice versa.
Subsequently, an evaluation was made of enhancing the rate of the IP3-sensitive release of [Ca2+]ER to the cytosol. The parameters of the neuron were fixed to the default values and the BK conductance set at 0.6 μS/cm2 (an intermediate value). By increasing the value of VM3 from 500 to 600, a higher level of [Ca2+]cyt is obtained. An abrupt release of Ca2+ from the ER boosts the [Ca2+]cyt from 5 to 6 μM (red lines). In the previous simulation (blue lines), corresponding to the effect of [Ca2+]cyt at 5 μM, the action potential train was found to brake at 721 ms. When the concentration of [Ca2+]cyt is increased, calcium acts on the BK channel, stopping the action potential train after the second action potential (Figure 5). It is observed that at greater CICR pumping rates, the level of [Ca2+]cyt rises by a calcium-induced calcium release process and/or by the direct action of IP3 on the calcium-IP3-R channel (by Schetter and Smolen in [59]).
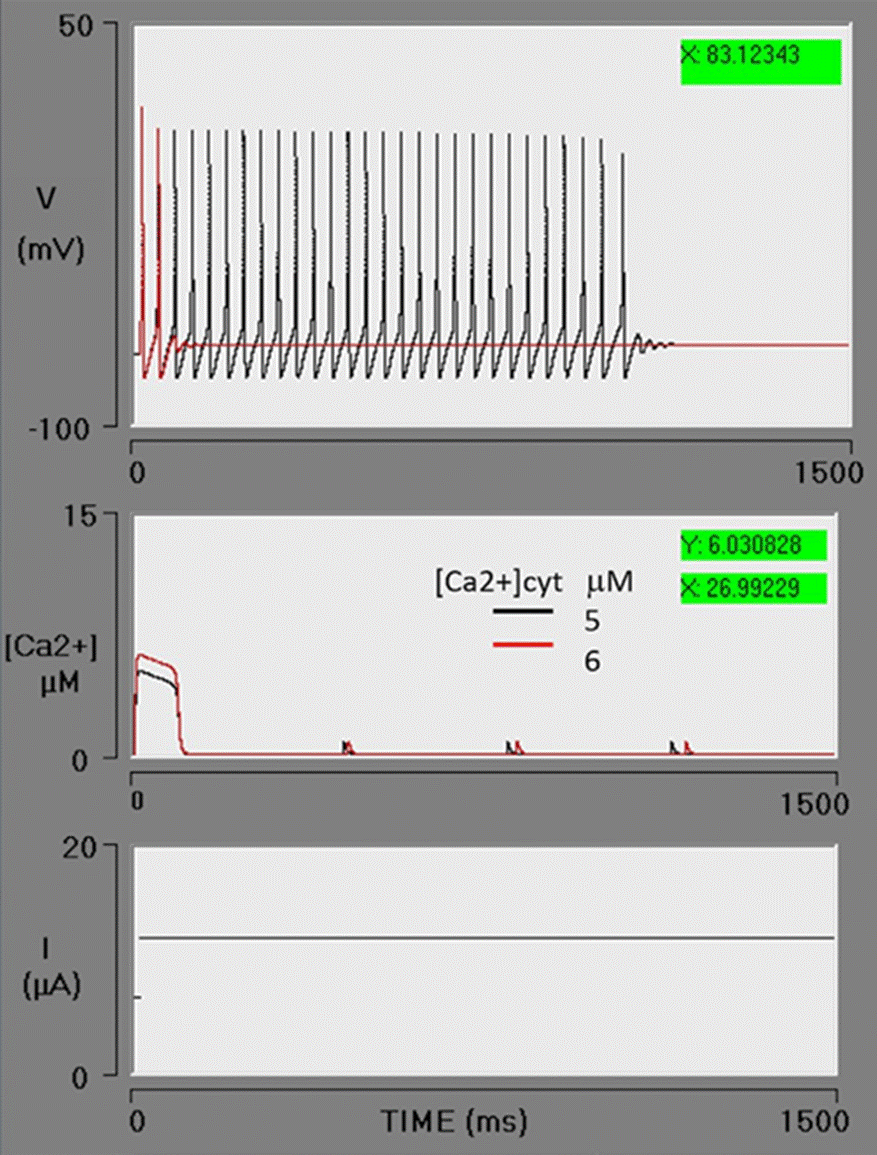
Figure 5 Effect of an enhanced Ca2+ efflux from the endoplasmic reticulum to the cytosol. An increment in VM3 from 500 to 600 μM/s causes a greater outflow of Ca2+ from the ER to the cytosol, leading to a rise in the cytosolic Ca2+ concentration from 5 to 6 μM. With an intensified activation of BK channels, the action potential train stops after the second firing. The lines in black depict the previous simulation, while the lines in red illustrate this simulation with an increased VM3 (red box).
An increment in VM3 to 700 μM/s generates a rise in [Ca2+]cyt to 7 μM. Under these conditions, the neuron stops firing immediately after the first action potential (Figure 6). Although the model of Goldbeter contemplates the action of IP3 on IP3-R and offers a good approximation of the experimental data, it does not provide a dose-response relationship. It has been documented in the literature that the higher the level of IP3, the greater the release of Ca2+ from the ER [62]. Taking the limitations of the Goldbeter model into account, this simulation reasonably resembles the IP3sensitive Ca2+ release from the [Ca2+]ER pool.
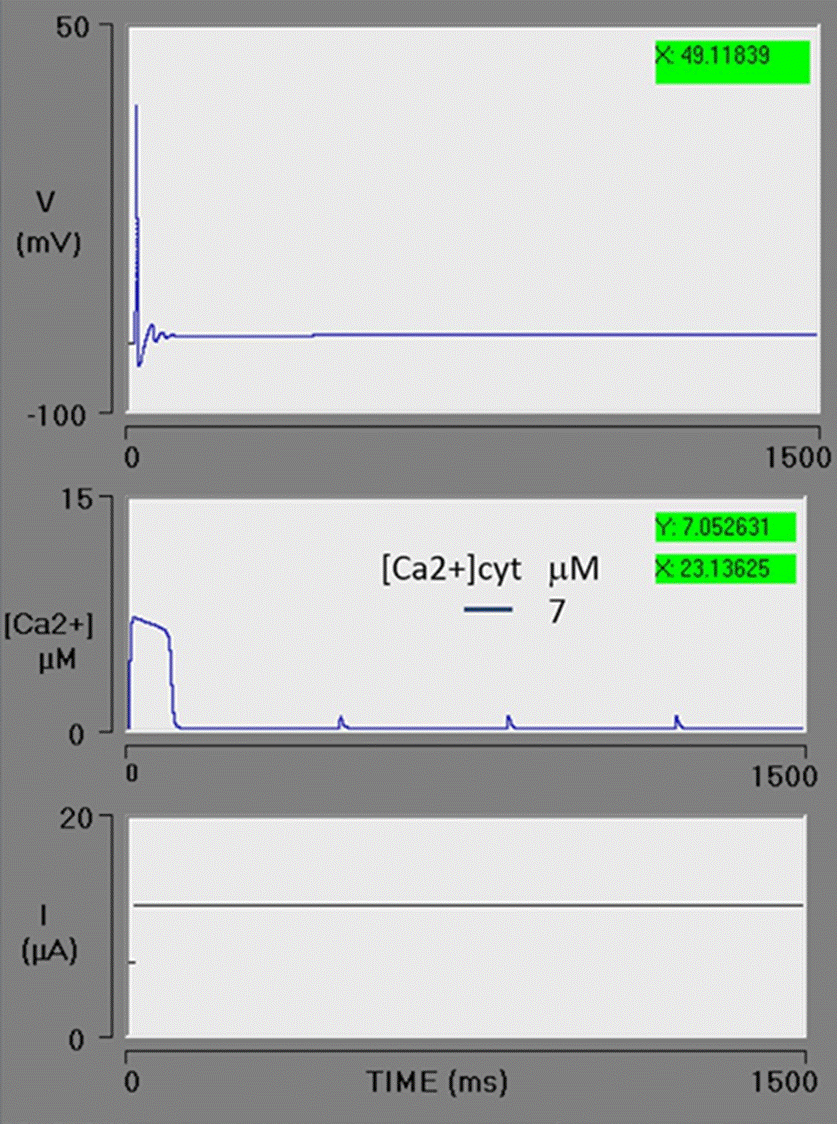
Figure 6 Spike train simulation with high efflux of Ca2+ from the endoplasmic reticulum (ER) pool. The maximum rate of Ca2+ efflux (VM3) = 700 μM/s, resulting in a cytosolic Ca2+ transient increase with an amplitude of 7 μM. The greater level of cytosolic Ca2+ activated the BK channels, immediately stopping the spike train.
According to the results, Ca2+ released from the ER to the cytosol can effectively gate BK channels, and the main effect is to stop the spike train (Figure 6). These findings are consistent with reported experimental data. The Ca2+ released from ER stores, specifically through IP3Rs but not RyRs, produces pauses in the firing of spiny projection neurons due to the activation of BK and SK channels [63]. The author proposes two Ca2+ signaling pathways:
(1) action potential → VGCC → RyR → BK & SK → sAHP (slow afterhyperpolarization); and
(2) mGluR/mAChR (metabotropic glutamate receptors / muscarinic acetylcholine receptors) → IP3 → IP3R → BK & SK → firing pause.
In the current contribution, a theoretical evaluation was made of the level of [Ca2+]cyt, mainly considering the interaction of IP3-Rs with BK channels. The findings support the possible existence of a microdomain. In places where the ER membrane and the cytoplasmic membrane are far apart, the diffusion and chelation will decrease the amplitude of the Ca2+ signal and this mechanism may not be activated. This depends, according to the results presented here, on the number of BK channels present in the membrane. The diffusion and chelation processes of Ca2+ are not contemplated in this model.
The effect of accelerating the action of the ATPase pump (SERCA) was explored under conditions of high Ca2+ efflux (the previous simulation). An increase in the K2 parameter (the threshold constant for pumping) from 1 to 2 μM decreases the concentration of [Ca2+]cyt from 7 to 3.4 μM. As can be appreciated, the action potential train is reversed and the neuron fires continuously during the simulated time (Figure 7).
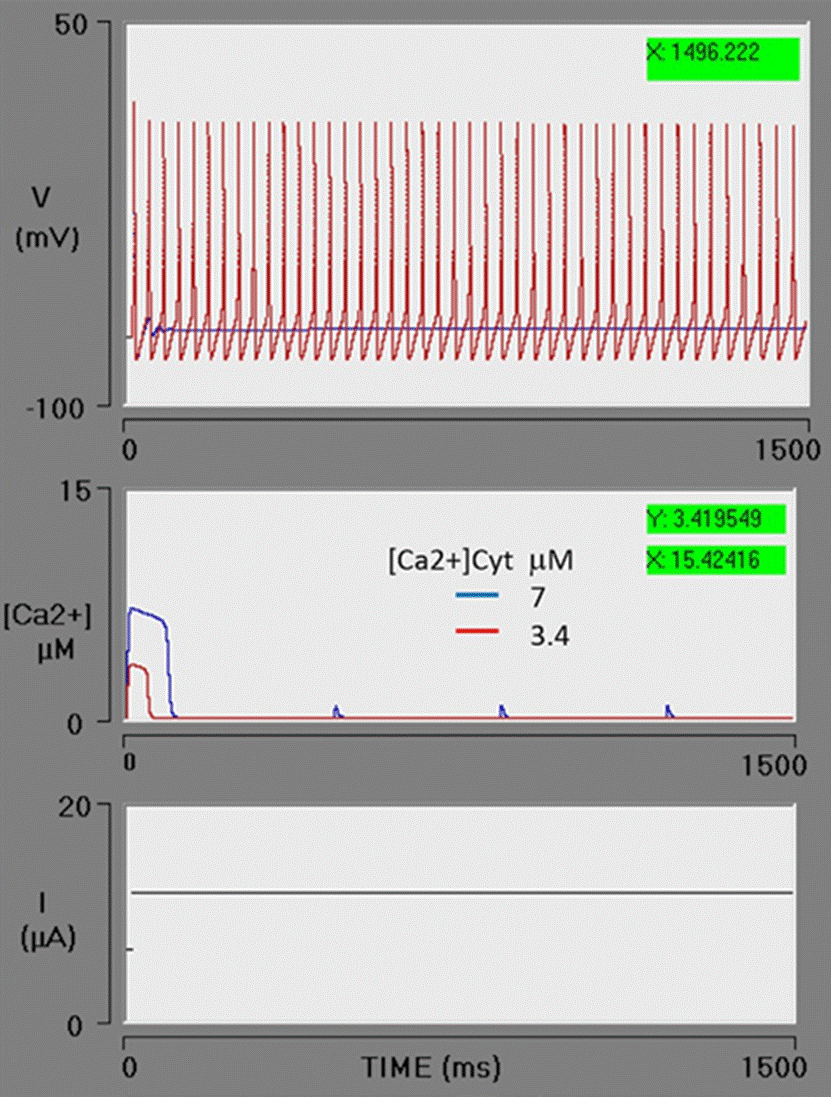
Figure 7 Ca2+ uptake from the cytosol by the SERCA pump. The action of the SERCA pump is increased by an increment in the K2 parameter (from 1 to 2 μM, being the threshold constant for pumping; red box). The concentration of cytosolic calcium decreases from 7 to 3.4 μM. Consequently, cytosolic calcium is below the threshold required for the activation of the BK channels and the neuron has a sustained action potential train. The blue line portrays the previous simulation (Figure 6), using the same value of VM3 (blue box) in this simulation. The red line depicts the present simulation (with the SERCA pump set at a higher rate).
Under physiological conditions, the PMCA pump and the SERCA pump are responsible for avoiding an excess concentration of [Ca2+]cyt, which could be toxic to the cell [22] [49]. Such an excess concentration of Ca2+ would inhibit IP3-R [22]. Calcium oscillations have been demonstrated to move like waves with an amplitude in the order of nM [21] [36] and a range dependent on their diffusion and binding with chelating molecules [18]. These oscillations have been proposed as signals for various cellular processes, including synaptic plasticity, regulation of neurotransmission, cell differentiation, apoptosis, embryonic development, and secretion [21]. The abrupt influx of Ca2+ into the cell by voltage-gated calcium channels in the plasma membrane activates BK channels and triggers a change in action potential frequency [18]. The results of the present simulation show how an abrupt, focused increase in [Ca2+] cyt from the endoplasmic reticulum store, very similar to those described as “spark”, favors the activation of BK channels and produces a pause in the action potential train. This would imply that, under certain conditions, a mechanism capable of stopping neuronal signaling is activated.
CONCLUSIONS
A theoretical study of the IP3-R/BK channel interaction was carried out by means of a simulator. Consequently, it was possible to modify the parameters to regulate the concentration of Ca2+ in the cytosol in order to monitor the effects. The variables considered are related to the flow of Ca2+ from cytosol: out of the cytosol to the ER (the SERCA pump) and to extracellular space (the PMCA pump), as well as into the cytosol from the ER (through the IP3-Rs) and from extracellular space (the VGCCs). Additionally, the conductance of the BK channel and the parameters of the Goldbeter model are included.
Some insights were provided into the general character of the IP3-R/BK channel interaction. (1) The [Ca2+]cyt concentration required to activate BK channels varies in accordance with the conductance of the channel. With a greater conductance, the concentration of Ca2+ necessary for activation is lower. (2) The BK channel is activated by an abrupt release of Ca2+ from the ER. This increase in Ca2+ is local and resembles spark. (3) The amplitude and duration of the abrupt efflux of Ca2+ from the ER depends on the difference in the concentration between the free [Ca2+]cyt and the free [Ca2+]ER. The higher the concentration of the latter, the greater the amplitude and duration of the efflux. (4) A rise in the concentration of [Ca2+]cyt increases the concentration of [Ca2+]cyt and favors the activation of BK channels. (5) An acceleration of the SERCA and/or PMCA pumps decreases the concentration of [Ca2+]cyt, thus reducing or avoiding the activation of BK channels. (6) A rise in [Ca2+]cyt activates the BK channels, leading to an immediate pause or stop of the spike train. This function will allow the neuron to generate a firing pattern in burts and under certain conditions be a possible mechanism for resetting or preventing sustained abnormal PA activities (7). The colocalization of the BK and IP3-R channels in a microdomain is a necessary condition for the manifestation of the following pathway in a neuron: IP3 → IP3-R → Ca2+ → BK channels → pause (stop). This sequence is the regulatory mechanism (8) For neurons with a low gBK, a high [Ca2+]cyt concentration, and a greater difference between this parameter and free [Ca2+]ER is necessary to activate BK channels. (9) In case of having an elevated level of gBK conductance, neurons activate the BK channels more easily. The aforementioned theoretical results help to explain the experimental data of Clements et al. [63] and are in accordance with the proposal made by these authors about the existence of Ca2+ signaling pathways that mediate BK channel activation according to the level of [Ca2+]ER.











 nueva página del texto (beta)
nueva página del texto (beta)


