1. Introduction

The Rio Grande rift is an important lithospheric scale feature associated with significant thinning of the crust and mantle lithosphere, high heat flow and low upper mantle seismic velocities (^{Keller et al., 1990}). One striking feature is the presence of low angle normal faults. The fault systems in the Rio Grande rift have been affected by considerable rotations, tilting and change in the stress field (^{Seager, 1981}). Thus, understanding the nature of the low angle normal faults is not an easy task. The post-Laramide stress regime is widely recognized from previous works (^{Baldridge et al., 1980}; ^{Morgan and Golombeck, 1984}; ^{Aldrich et al., 1986}; ^{Morgan et al., 1986}). They suggest that the opening of the Rio Grande rift is divided in two distinct periods associated to different stress regimes. The first phase of deformation occurred from 30 to 18 Ma, forming shallow basins bounded by low-angle normal faults. This period is associated with volcanism and is attributed to thinning of hot lithosphere with a shallow brittle-ductile transition (^{Morgan and Golombeck, 1984}; ^{Keller et al., 1990}; ^{Baldridge et al., 1995}). Such low angle normal faults are only known from isolated areas, and their nature is still a point of debate. A later rifting phase, beginning 10 Ma is associated with classic Basin and Range style block faulting ^{(Keller et al., 1990}) and the delineation of the present interconnected rift basins and flanking uplifts. In contrast to these conclusions, ^{Henry and Price 1984}inferred that the extension direction during the early phase of rifting was East-West and then it switched to Northwest-Southeast recently. The current stress field in the Rio Grande rift is West-Northwest, although the stress field may vary locally (^{Zoback and Zoback, 1980}, ¹⁹⁸⁹). According to Aldrich et al. (¹⁹⁸⁶) many faults and dikes are associated with reactivated structures and their orientations cannot be used to infer the orientations of the principal stress. Using dike orientations in plutons, in addition to detailed dating studies, they found the orientation of the least compressive stress was N-NE-S-SW and during the latter phase was associated with West-Northwest to East-Southeast extension. However, Aldrich et al. (¹⁹⁸⁶) and ^{Chapin et al. (1994}) regarded early Miocene dikes in the roofs of plutons as being the best indicators of regional stress orientations since these are only known at two locations in the rift. Therefore, they may not be representative of the regional stress regime. In this study, fault slip inversion has been used to determine the state of stress adjacent to major low angle normal faults in the southern Rio Grande rift in order to clarify the orientations of the principal stresses during rifting. One of the biggest questions in the southern Rio Grande rift is determining if normal faults were formed in two phases of deformation or they evolved in a single progressive deformation event. Extensive faulting and tilting are inferred to have occured during two distinct extensional phases in the Rio Grande Rift on the basis of structural studies (^{Collins et al., 1994}; ^{Henry and Price, 1984}; ^{Aldrich et al., 1986}; ^{Morgan et al.}, ¹⁹⁸⁶; ^{Seager et al., 1984}).

This study focused on two ranges in the southern Rio Grande rift which expose low angle normal fault systems, the first in the Franklin Mountains at Anthony Gap, the second exposed in the East Potrillo Mountains (Figure 1). These two ranges are found at the northern margin of the Chihuahua Trough, a major Mesozoic basin. Through detailed structural analysis we attempted to constrain the stress field during the formation of the normal faults, determine if the faults are rotated due to younger extensional phases and analyze the relationship between the low angle faults and range uplift.

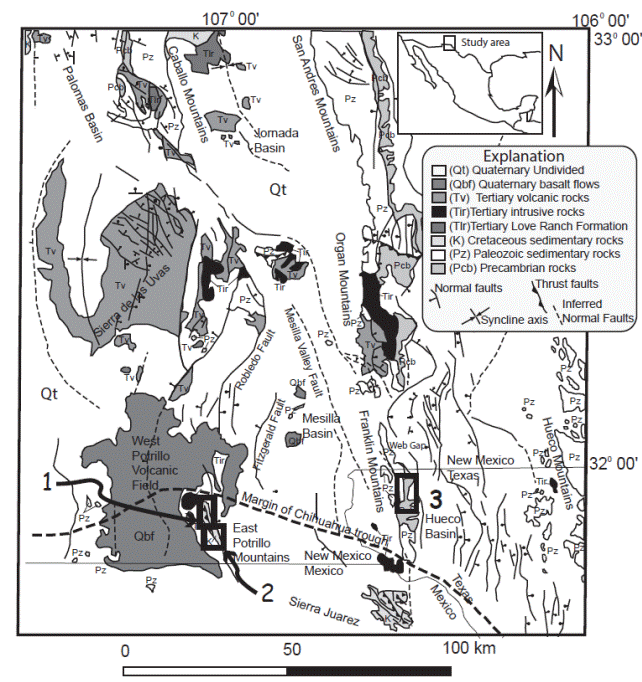
Figure 1 Geological map of the region. The two studied areas are the East Potrillo Mountains (insets 1 and 2) and the Franklin Mountains (inset 3). Both ranges are located at the northern margin of the Chihuahua trough (modified from ^{Ruiz, 2004}). 

2. Methods

The main assumption necessary to obtain the stress tensor based on fault orientation is that the direction of the tangential traction on the plane tends to be parallel to the slip direction; this tangential traction is also assumed to be parallel to the shear stress (^{Ramsay and Lisle, 1997}). In this way, we assume that the increment of the principal strain axes coincide with the principal stress axes. This is the basic assumption to apply stress inversions. Therefore, if the tangential traction can be determined on a variety of fault planes formed at the same time in a region, it may be possible to make inferences about the regional stress field (^{Angelier, 1984}). The direction of the maximum resolved shear stress is constrained by experiments and observations to lie in the plane of the fault and in the σ ¹-σ ³ plane. Mohr-Coulomb behavior allows making several assumptions about the orientations of the principal stresses. These assumptions include the fact that fractures form at ~30° to σ ¹ and the least compression direction, σ ³, generally lies at ~60° to the fractures. However, low angle normal faults are difficult to reconcile in terms of stress inversion as they cannot be easily explained by assuming Mohr-Coulomb failure criteria (^{Davis et al., 1983}).

In the Potrillo Mountains, faults with the best slickenlines were found in silica-cemented calcareous siltstones, which are common in the Hell-toFinish formation. Slickenlines within major fault zones are rarely observed due to poor exposures and pervasive cataclasis. Therefore, our analysis focused on minor faults with small displacements, which may be more appropriate for stress inversion than large displacement faults (^{Erslev, 2001}). At each outcrop, fault strike and dip as well as slickenline trend/plunge, and shear sense were measured. All data were inverted using the inverse methods of ^{Michael (1984}), and the inverse method of ^{Marret and Allmendinger, (01990} to estimate the regional stress tensor. The data were collected using the regional geological map of ^{Seager and Mack (1994}) as a guide, we identified the major structures and collected the field data in general. Subsequently, it was possible to analyze the stress tensor in a regional sense by comparing our results with the data using only the geological map information.

3. Data

We used fault data from existing 1:24000 geological maps (^{Seager and Mack, 1994}; ^{Harbour, 1972}; ^{Kelley et al., 1983}) as well as field data using topographic maps as field guide. Because slickenline data are very important in stress and strain analysis, we focused on fault striations. In addition, we collected other structural data such as extensional veins, fold limb orientations, cleavage planes and bedding directions. This data set is used to analyze differential and mean stresses using the Mohr circle relationships of the associated faults. In the Anthony Gap area, we collected fault data from the high angle normal faults which connect to the large displacement low angle normal faults for this analysis.

3.1. FRANKLIN MOUNTAINS

Low angle normal faults in the northern Franklin Mountains have been described by several researchers (^{Harbour, 1972}; ^{Seager, 1981}; ^{Kelley et al., 1983}; ^{Figures 1987}; ^{Ruiz, 2004}). Kelley et al., (¹⁹⁸³) and Figures (1987), who recognized large displacement gradients form North to South across the normal faults, with displacements close to zero at Web Gap and approximately 1000 meters at the state line (Figure 2). This differential displacement requires that the hanging walls of the normal fault system undergo rotation in the axis oriented normal to the fault as a consequence of the differential displacement. To quantify the rotations in the axis normal to the fault, three cross sections (Figure 3 and 4) were drawn across the region of the largest gradient of displacement (Box in Figure 2).

Figure 2 Geological map of the Anthony Gap area, northern Franklin Mountains (after ^{Kelley et al., 1983}; ^{Figures, 1987}, ^{Harbour, 1972}). 

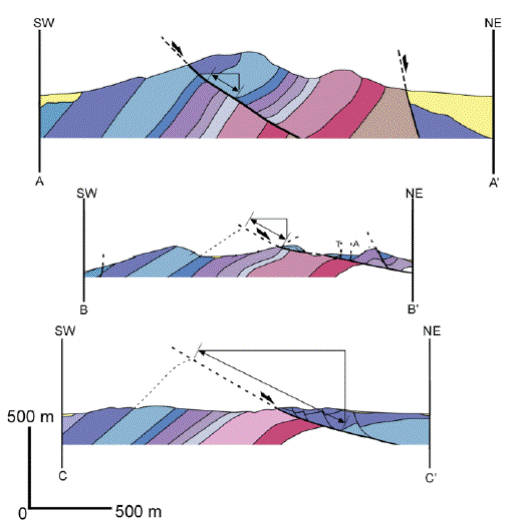
Figure 3 Cross sections A-A’, B-B’, and C-C’. Cross section A-A’ is redrafted from ^{Kelley and Matheny (1983}). On section B-B’, T indicates displacement toward the viewer, A indicates displacement away form the viewer. Right triangles above the sections show horizontal and vertical displacements inferred form stratigraphy. Color scheme for units is the same as Figure 2. 

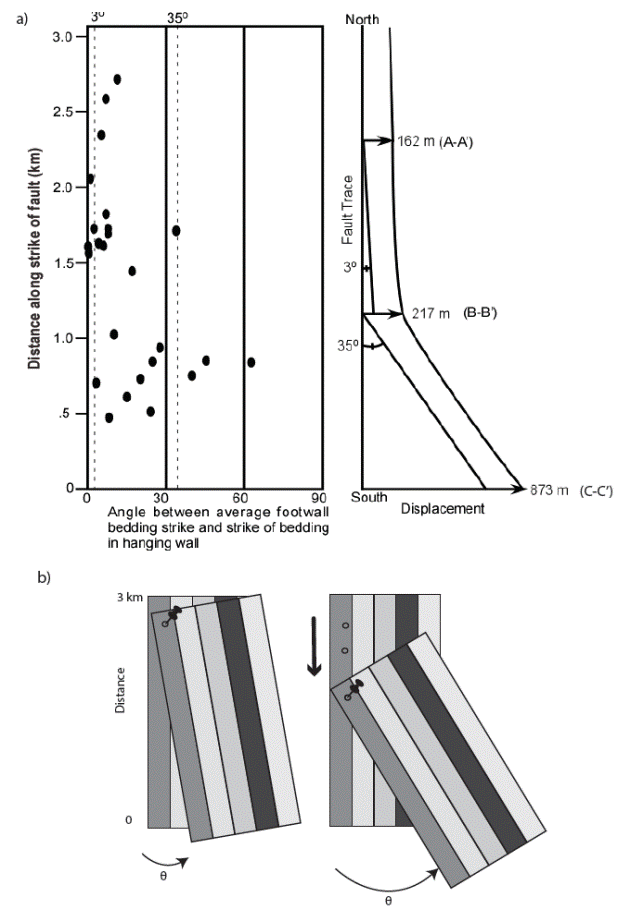
Figure 4 Plot of the angle between average footwall bedding strike and individual bedding measurements in the hanging wall in the box shown in Figure 2. Adjacent diagram shows inferred vertical axis rotations predicted from differential displacement along the normal fault. 

These sections show that horizontal displacement increases from ~160 meters at the location of section A-A’ to ~220 meters at section B-B’, and to 880 meters at section C-C’ (Figure 3 and 4). This slip distribution implies that the degree of rotation of the hanging wall between section A-A’ and B-B’ is less than that between B-B’ and C-C’. If the rotation occurs only by a rigid body, then the displacement gradient gives a direct measure of the angular rotation. However, this is not the case because rotation and displacement occur at the same time (Figure 4b). To quantify this effect, bedding in the footwall was used as a reference frame to estimate the angular rotation. The average bedding plane within the footwall in the area of the box in Figure 2 was calculated. Then the angle between the bedding planes in the hanging wall was measured with respect to the average bedding in the footwall and plotted as a function of the along strike distance. If the axis of rotation occurred entirely by rigid-body rotation the angle between bedding in the footwall and hanging wall should mimic that one estimated by the displacement gradient (Figure 4). These measurements should be taken within the same lithology which in this study was in the Panther Seep and Tuna formations (Fig. 2). Inspection of Figure 4 shows that in most cases the angle between bedding planes is less than that one predicted by rigid body rotation alone, this is due to displacement that occurred previously at different piercing points which imprinted that rotation angle before (Figure 4b). It is worth noting that we only collected bedding information from La Tuna and Helms formations (Figure 2) to avoid errors from different lithology. It is possible that other events of deformation caused variations of angles of bedding planes. For example, there are different thrust sheets in the study area which preceded normal faulting and could have caused variations in bedding. Therefore, we are afraid that this may be source of errors in our interpretation. On the other hand, there is a general increase in discordance between the hanging wall and footwall as displacement increases indicating rigid-body rotation was an important process. Other processes might have accommodated the rotation of the hanging wall, given the observed displacement gradient. In the Northeast corner of the box in Figure 2, two-left lateral strike slip faults occur, and are approximately parallel to the strike of the normal faults. These faults are associated with folding of the hanging wall strata and a dramatic change in bedding strike (figures 2 and 3). These faults do not penetrate the footwall of the normal fault system, have a short strike length, and occur in the region of the largest displacement gradient. These characteristics suggest that these faults were formed during normal faulting. Kinematically, these faults are consistent with accommodation of counter-clockwise rotation of the hanging wall. Therefore, it is likely that bending and rotation of the hanging wall was in part accommodated by left lateral strike slip faulting in the hanging wall of the fault.

Another geometric feature of the normal faults in the northern Franklin Mountains is the development of hanging wall synclines (Figure 2 and 3). The synclines trend to the N-NW, and are parallel to fault strike, have gently East dipping western limbs adjacent to the faults, flat hinges and moderately East dipping eastern limbs. The fold axes are shallowly plunging and generally perpendicular to the inferred fault slip direction.

Cutting the hinges of the folds there are numerous small displacement normal faults, many with a conjugate geometry. Numerous tension veins occur and generally bisect the acute angle between the conjugate fault sets. Stereographic projections of poles to faults planes, poles to tension veins, and poles to bedding, show that all three structures are coaxial with respect to the syncline axis (Figure 5) demonstrating that all these structures probably formed during a single deformation event. The folds are geometrically similar to extensional fault propagation folds which are observed in nature (^{Shaw et al., 1997}) and numerically modeled (^{Suppe et al., 1990}; ^{Hardy and McClay, 1999}). The tightness of the synclines is clearly related to fault displacement with the folds dying out to the North and tightening to the South.

Figure 5 Stereographic projections from Franklin Mountains. a) Poles to bedding for outcrop shown in Figure 6. b) Poles to calcite veins for the same outcrop. c) Poles to fault planes for same outcrop. Note poles in a, b, and c share a common fold axis (shown by star). d) Poles to bedding for all beds shown in Figure 4. Star indicates inferred fold axis. e) Poles to first generation calcite veins. f) Poles to second generation calcite veins. g) Fault planes with slip direction indicated. h) Calculated greatest compression axis (red squares) and least compression axis (white squares) estimated from inversion of the data in h). 

In order to analyze the stress-states during normal faulting and folding, small scale normal faults and associated calcite veins were studied, due to these structures have small displacement and are most likely to be representative of the instantaneous deformation (^{Erslev, 2001}). Stereographic projections shown in Figure 5 summarize the data from the northern Franklin Mountains. As can be seen, most faults strike North-Northwest parallel to the axis of the range and have steep to moderate dips, with nearly down dip slickenlines. Stress inversion using the ^{Michael code Michael, 1984}, of the data shows an extension direction towards East-Southeast-West-Northwest with a shallow plunge. The shortening direction is subvertical. Poles to calcite veins confirm a stretching direction towards East-Northeast-West-Southwest, approximately perpendicular to the trend of the range (Figure 5).

A further constraint on paleostress state can be obtained from the study of conjugate fault sets. Most of the conjugate fault sets have dihedral angles (the acute angle between the fault sets) which are less than the 60o angle, as predicted from the Mohr-Coulomb failure criteria (^{Ramsay and Huber, 1983}). Additionally, the faults frequently have irregular traces turn into calcite filled veins along their trace. These geometric features are consistent with the conjugate faults being transitional tensile fractures (^{Engelder, 1999}). Transitional tensile fractures were formed where the least compressive stress was tensile. Such fractures were described according to the parabolic Griffith failure criteria, which predict a closure of the dihedral angle as the stress field becomes more tensile (^{Ramsay and Huber, 1987}). Failure criteria in Mohr space is defined as:

τ2=4T02+4T0σn Ecuation 1

where τ is the shear stress, T⁰ is the tensile strength of the rock (T⁰=C⁰/2, with C⁰=cohesive strength) and σ ⁿ is the normal stress (^{Ramsay and Huber, 1987}). This equation can be solved for magnitudes of the principal stresses if the values of T⁰ are known and the dihedral angle can be determined. This is solved by differentiating equation 1 and solving for values where the tangents to the parabola are perpendicular to the predicted 2θ (twice the angle between the fault plane normal and the greatest compressive stress) derived from the dihedral angle between the faults. This gives values for shear and normal stress on the failure envelop that are tangent to the Mohr circle at failure, which fixes the radius of the Mohr circle, the mean stress and magnitudes of the greatest and least compressive stress, as long as the dihedral angle is small. For large dihedral angles (greater than 45o) the parabola in Mohr space becomes effectively linear and many different Mohr circles become tangent to the envelop making a unique solution impossible. Fortunately, the maximum dihedral angle observed in this study is ~45o, with a mean dihedral angle of 36o (Figure 6).

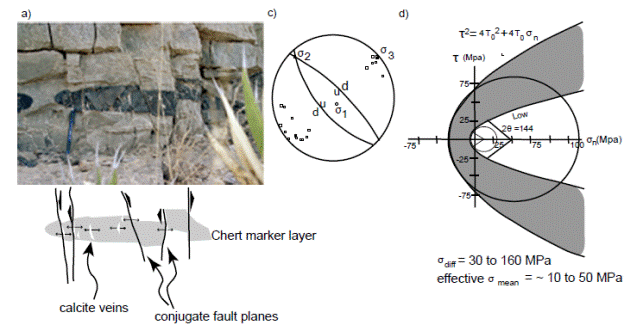
Figure 6 Diagram illustrating how stresses are estimated from geometry of conjugate fault sets. a) Photograph of outcrop with conjugate normal faults cutting the Berino Formation at Anthony Gap. b) Sketch of photograph showing relationship between calcite veins and the faults. c) Lower hemisphere equal area projection showing the orientations of the principal stresses derived from the conjugate faults. Dots represent poles to calcite veins which confirm the orientation of the least compressive stress derived form the conjugate faults. d) Mohr diagram illustrating the Griffith failure criteria and inferred Mohr circle derived from the geometry of the fault sets. Smaller envelope is calculated using T⁰ values for Carrera Marble, outer envelope uses Blair Dolomite values. Gray shaded region corresponds to the range of likely stresses during faulting recorded in the Franklin Mountains. 

Values of T⁰ were chosen to bracket the likely range of strengths of carbonate rocks, as limestones and dolomites dominate the rock types exposed in the Franklin Mountains and no rock mechanics experiments have been conducted using materials from the Franklin Mountains. For a lower bound, To for Carrera Marble (^{Suppe, 1985}) was used. This is a coarsely crystalline marble and has very low tensile strength relative to rocks with a finer grain size. For an upper bound, To values for Blair dolomite (Suppe, 1985) were chosen as this rock has a very high tensile strength comparable to diabase and gabbro. Only maximum values for differential stress and effective mean stress can be made because all available experimental data have been collected on dry rocks, which are much stronger than rocks that deform in the presence of fluids (^{Ramsay and Chester, 2002}). Additionally, the estimated principal stresses and mean stress are effective values because pore fluid pressure lowers the values of the principal stresses due to hydrostatic pressure counteracting applied compressive stress. Since only maximum values for the effective stresses and differential stress can be obtained the maximum dihedral angle of 45o was used in the calculations. This also provides a maximum estimate, since faults with smaller dihedral angles will result in stresses with smaller values.

The results suggest that the differential stress during faulting in the Franklin Mountains range between 30 and 160 MPa and the effective mean stress range between 10 and 50 MPa. To our knowledge, these are the only estimates of differential and mean stress which have ever been made based on the geometry of faults as input. The effective mean stresses are consistent with the faults forming in the upper five kilometers of the crust assuming that hydrostatic pressure was equal to or less than the lithostatic pressure.

The final feature of the Franklin Mountains is the occurrence of transverse normal faults which cut across the range at a high angle. These faults generally have small displacements and are locally associated with large fault parallel calcite veins (up to 1 meter in width). Cross cutting relationships between calcite veins demonstrate that these veins are younger than northwest trending veins associated with range parallel faults. Unfortunately, none of the planes of the transverse faults is well enough exposed to collect the data needed for fault slip inversion. However, the geometry of the veins, orientations and displacements on the faults are all consistent with the faults forming during range parallel extension. However, the faults do not appear to cross cut the northwest trending faults, and instead terminate at the low angle faults. This suggests that these faults are likely linked to displacements on the low angle normal faults. Additionally, the faults are most common where the displacement along the low angle normal faults is largest, and disappear to the north as fault displacement decreases, supporting the interpretation that the faults were formed synchronously with displacement on the low angle faults.

3.2. POTRILLO MOUNTAINS

The complexity of deformation in the Potrillo Mountains makes geometric analysis of low angle normal faults a difficult and uncertain task (^{Carciumaru et al., 2011}). Therefore, we focused only on fault slip analysis, and analysis of tension vein arrays as these data can be easily correlated with the normal faults. ^{Seager and Mack (1994}) provide detailed descriptions of the structural geology of the Potrillo Mountains (Figure 7 and Figure 8). They describe the low angle normal faults which cut the central Potrillo Mountains, and concluded that the largest of the faults, exposed in the central Potrillo Mountains, is an extensional detachment surface active during Miocene rifting. This was based on the low angle of the structure and profound differences with the structures between the hanging wall and the footwall. Specifically, they noted that large scale Laramide folds and thrust faults predominate in the hanging wall, whereas the structure of the footwall is much less affected by Laramide contraction. Due to the effects of Laramide folding, no suitable stratigraphic or structural piercing points are found, thus it is difficult to estimate displacement on the fault system (Seager and Mack, 1994). However, intensity of fault gouge, stratigraphic constraints and structural discordance require a minimum of several hundreds of meters of displacement, although this value could be greater.

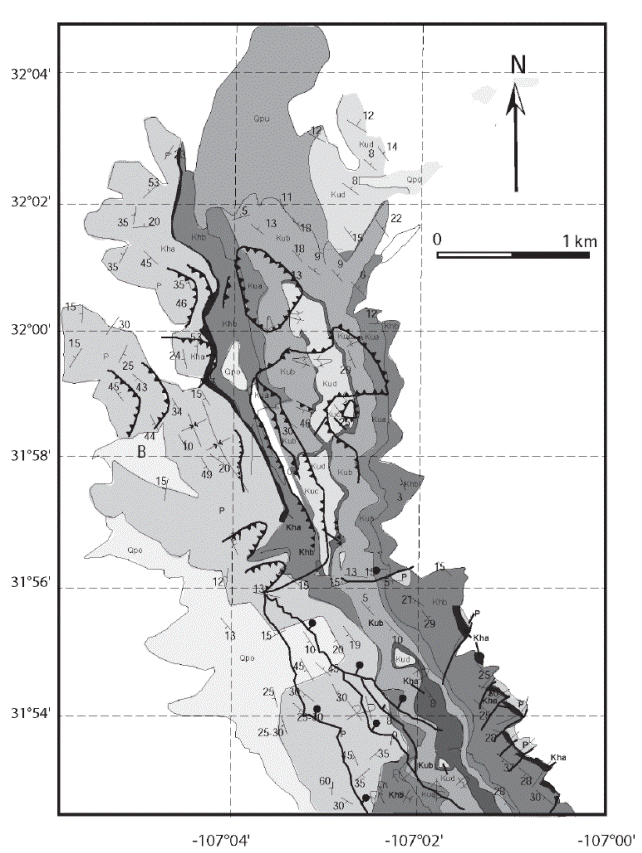
Figure 7 Geological map of the northern part of the East Potrillo Mountains. The two main formations are Hell-to-Finish and U-Bar, overlying Permian rocks. The general trend of the structures is oriented N36o W (after ^{Seager and Mack, 1994}). 

Figure 8 Geological map of the southern part of the East Potrillo Mountains. The two main formations are Hell-to-Finish and U-Bar, overlying Permian rocks (after ^{Seager and Mack, 1994}). 

The low angle normal faults can be divided into two geometric groups (Figure 9). The first group has northeast strikes, shallow dips and down dip slickenlines. Based on cross cutting relationships these faults appear to be the oldest set of normal faults exposed in the Potrillo Mountains (^{Seager and Mack, 1994}). These faults are often associated with bleach zones around the faults with a strong fault parallel cleavage. The faults contain 10 to 50 cm thick gouge zones cored by brecciated cataclasite. Slickenlines on the faults are well developed, but are often obscured by a breccia. Applying fault slip analysis to this population of faults indicates that the faults record North-Northeast directed subvertical extension (figures 9a and 9b).

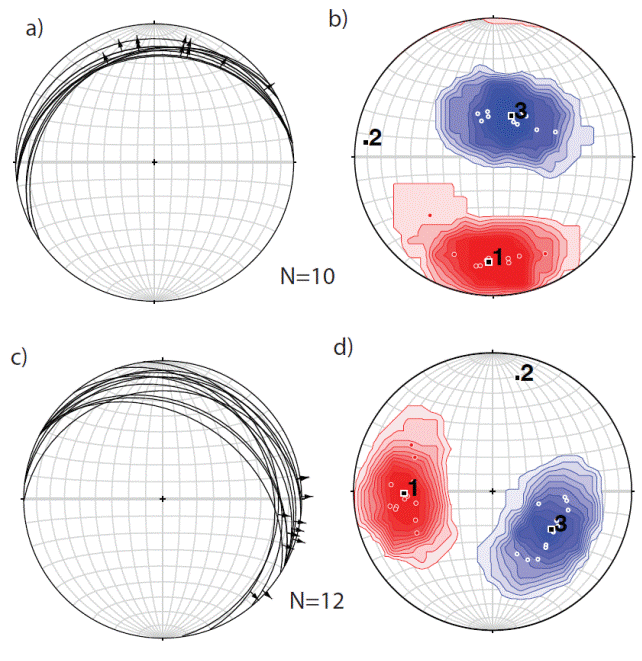
Figure 9 Stereographic projections from Potrillo Mountains using the FaultKin7 software (^{Allmendinger et al., 2012}). a) First generation fault planes, arrows show movement direction of the hanging wall. b) Stress tensor solution using the code of ^{Michael (Michael, 1984}) (black squares), in addition the countours using the Kamb method (Allmendinger et al., 2012) with one sigma as significance level. c) Second generation fault planes, arrows show movement direction of the hanging wall. d) contours of the kinematics solution for the second generation. 

The second set of faults has a Northwest strike, shallow dips to the northeast and highly oblique slickenlines that plunge to the East-Northeast (figures 9c and 9d). Slickenlines are often nearly strike-parallel suggesting a significant transcurrent component to the displacement despite the shallow dips of the faults. In other ways, these faults are geometrically and texturally similar to the older set of low angle faults, which appear to sole into. Fault slip analysis suggests that these faults recorded East-Southeast subhorizontal extension with a moderately Southeast plunging shortening direction. Kinematic data are consistent with right lateral oblique normal displacement, quite distinct from the earlier set of normal faults. Geometry and kinematics of both sets of faults is quite distinct from normal faults exposed in the Franklin Mountains.

To further constrain the orientation of the least compressive stress calcite veins associated with the normal faults were analyzed (Figure 10). The average orientation of the veins is approximately East-West, with steep to vertical dips as shown in the rose diagram of Figure 10. This geometry is consistent with North-Northeast directed horizontal extension. This is also consistent with extension direction estimated from the fault slip analysis performed on normal faults with North-Northeast plunging slickenlines. This is in agreement with the fact that the majority of the veins are found in the hanging wall of the large low angle detachment fault which cuts the central part of the East Potrillo Mountains.

Figure 10 Map of the calcite veins in the central part of the East Potrillo Mountains, showing the planes and the poles to the planes. Also, the rose diagram shows the general tendency of the data. 

4. Discussion and conclusions

The study of ^{Carciumaru and Ortega (2011}) from low angle normal fault exposures in the Franklin and Potrillo Mountains indicate a polyphase deformation history and cannot be reconciled with a single progressive deformation event. The oldest fault sets in the Potrillo Mountains appear to have formed during North-Northeast directed horizontal extension. ^{Seager and Mack (1994}) inferred, based on correlations with regional geology that these faults were formed during an early Miocene phase of extensional deformation. The newly collected data on the Rio Grande fault system support this interpretation as they demonstrate this fault system was formed in a stress field unlike from any other population of normal faults here studied.

Additionally, Miocene patterns of sedimentation within the rift are consistent with early rift basins trending to the Northwest, as well as North-Northeast extension (^{Seager and Mack, 1994}).

The second set of low angle normal faults in the Potrillo Mountains is distinct in geometry and kinematics to faults found in the Franklin Mountains and the older set of faults found in the Potrillo Mountains. Fault slip analysis on these faults indicates that they record East-Southeast extension with a moderate Southeast plunging extension direction. This stress field is similar to the East-Northeast horizontal extension inferred for the Franklin Mountains, although the inferred shortening direction is distinct. It is possible; perhaps even likely, that the orientation of these faults was in part controlled by the orientation of the preexisting low angle normal faults. This is indicated by the fact that the two fault sets appear to merge along strike. If true, then the geometry of the faults would not be fully representative of the stress field in which they were formed. Therefore, they may have formed during the same deformation event recorded in the Franklin Mountains. Alternatively, the faults may have formed during an intermediate stage of extension. If this interpretation is correct, this intermediate stage would be largely transtensional as is indicated by the highly oblique nature of the slickenlines. However, similar faults have not been found regionally, therefore the reactivation interpretation is preferred.

Low angle normal faults in the Franklin Mountains contrast strongly with faults in the Potrillo Mountains because they appear to record a single episode of extension. Additionally, the stress field for the faults is generally consistent with the extension direction inferred from the orientation of Quaternary normal faults found in both the Messilla and Hueco Bolson’s which flank the range. Furthermore, ^{Zoback and Zoback (1980}), based on the alignments of volcanic centers in southern New Mexico (Potrillo volcanic field), inferred an East-West oriented extension direction. Additionally, the data indicate that faults have not been significantly tilted following formation. A further observation is that fault displacement increases to the South as the elevation of the Franklin Mountains increases, suggesting that this displacement is related in a gross way to the uplift of this Mountain range. All of the features of the low angle normal faults in the Franklin Mountains are consistent with the faults forming relatively recently, as these Mountains were uplifted. This interpretation is further supported by recent ₄₀Ar/₃₉Ar dating of jarosite from fault gouge in the Franklin Mountains which indicates a low angle fault movement in the last 6 Ma (^{Lueth et al., 1998}).

The late transverse faults in the Franklin Mountains indicate range parallel extension, distinct from that inferred from the low angle faults. The geometry of the faults is consistent with synchronous formation with motion on the low angle faults. ^{Axen and Wernicke (1989}) emphasized the role of isostatic rebound of the footwalls of the normal fault systems due to tectonic denudation. Their model emphasizes vertical displacements on a plane parallel to tectonic transport (plane strain) and did not address the effects of an along strike displacement gradient, like that seen in the Franklin Mountains. Since the normal fault footwall is denuded more to the South than to the North, the amount of footwall rebound would be expected to vary along strike. This type of gradient would produce flexure of the footwall parallel to strike. In turn, flexure leads to extension along the length of the flexure, providing a kinematic explanation for the development of the transverse faults. The magnitude of extension accommodated in this way would be small (< 10 %) given the flexure wavelength (~4 km) consistent with the small displacements on the transverse faults. Displacements on the low angle normal faults also resulted in counterclockwise vertical axis rotation of the hanging walls of the faults. This rotation ranged from 3o in the North to as much as 35o in the South. Rotations of this magnitude have been measured paleomagnetically in the Española basin of the northern Rio Grande rift (^{Salyards et al., 1994}). This indicates that this process is wide spread within the Rio Grande rift. Notably the faults have listric curves (spoon shape), resulting in an arcuate fault trace. These fault traces are similar to those arcuate spoon shaped fault traces common in the map pattern of Quaternary normal faults in southern New Mexico (see Figure 1). This suggests that faults with similar listric geometry underlie much of the southern Rio Grande rift. Overall the geometry and kinematics of the low angle normal faults is consistent with two phases of extension. The first phase of extension, is based on regional correlations, likely occurred in the Early Miocene, following wide spread volcanism (^{Chapin et al., 1994}). The second phase of extension has occurred over the last 10 Ma, and has had a dominantly East-West extension direction and has been accompanied by small-volume basaltic volcanism (^{Seager and Mack, 1994}).

This study shows that low angle normal faults were formed during extensional phases in the southern Rio Grande rift. Prior studies about the rift have concluded that low angle normal faults were formed due to tilting of initially high angle faults (^{Seager, 1981}; ^{Kelley and Matheny, 1983}; ^{Lewis and Baldridge, 1994}). These prior studies inferred that the thermal structure of the Rio Grande rift was fundamentally different from that one which is present today, leading to a shallow brittle ductile transition producing low angle faults (^{Morgan and Golombek, 1984}; ^{Keller et al., 1990}; Baldridge et al., 1995). The presence of young low angle normal faults challenges this view. The results also suggest that low angle normal faults are common in the upper crust and form basin bounding normal fault systems which influence the development of surface topography. Large displacement gradients along the faults also produce vertical axis rotations independent of strike slip faulting and range parallel extension due to flexure of the footwall. The stress fields associated with low angle fault systems varied both in time and space with each of the fault systems forming in response to distinct stress fields. However, the overall pattern of deformation is consistent with two episodes of deformation, the first with North-Northwest directed extension and the second with East-West extension.

The results show that the Franklin Mountains underwent major low angle normal faulting during uplift of the range. A detailed study of the rift uplift in New Mexico using thermocronology is described by ^{House and Kelley, 2003}. In contrast, low angle normal faults in the Potrillo Mountains were formed during an earlier phase of deformation and have likely been tilted from their initial orientation (^{Carciumaru and Ortega, 2011}). These results support a two-phase extension model for the Rio Grande rift and demonstrate that low angle normal faulting occurred during both phases of extension and is in fact characteristic of the southern Rio Grande rift.

This article has reviewed the structural aspects of this region. We observe that the state of stress in Franklin and Potrillos Mountains does not necessarily represent two different periods. Stress inversion should be performed from data that represents a homogeneous state of stress. It is preferred to use contemporaneous fault data when reconstruction studies are performed. However, this paper is focused on determining if Rio Grande Rift was formed during two phases of extension. So, using the criterion of contemporary faults is not very adequate. For this reason, we have decided to analyze the faults arguing that the data belong to a homogeneous state of stress.

In a previous article, ^{Carciumaru and Ortega, 2011}, demonstrated that low angle normal faults can be analyzed by a back tilting technique using the cluster analysis method (^{Yamaji, 2000}). In that study, Carciumaru and Ortega (²⁰¹¹) demonstrated that this data set can be represented in a homogeneous state of stress. The error range was low after performing a statistical analysis because the data converged to a single stress tensor. The method is based on a comprehensive combinatorial analysis. Data are analyzed by systematically varying the number of samples. This is done to eliminate outliers, and to reduce variability in case of epistemic errors. Once a series of input data is obtained, a new reference system results by slightly rotating the components of the faults. This simulates a back tilting.

Convincingly, it is inferred that these data belong to a homogenous state of stress. In the present article, we have used virtually the same data set, so we strongly believe that the analysis of stress is based on homogeneous data.

It is important to note that the study conducted on the faults associated to rocks of different strength appear to have a high range of variability. Although it is preferable to know exactly the dynamic parameters of the rocks, this is not always possible because these studies are costly. We consider that an average rock range reported in the literature is sufficient for a general analysis. We observed that the origin of these faults occurs in a range of 40 to 150 MPa. We know that for Mexican earthquakes the stress drop is 4 MPa. The mean stress of these faults is of one order of magnitude greater than that observed in the crust in case of tectonic earthquakes. Probably the main reason is that the tensional stress requires higher strength at the beginning of the first crack rupture than a pure shear stress during an earthquake.

This analysis is an important achievement in geology. It is well known that stress inversion with fault data only uses angle measurements (strike, dip, rake); therefore, they do not contain absolute measurements. In general, the studies of structural geology rarely report absolute magnitudes of the stress values. In this article, we could identify at least a range of values.

As a practical example, if absolute stress values are known for a geomechanical analysis then, we can better predict a blowout during a drilling process. Rarely rotational changes are reported in structural geology studies when stress-strain inversions are performed. It is well known that the simplification of stress-strain tensor is made by assuming a symmetrical strain tensor. This symmetry appears when the rotation part is canceled. We have observed that the rotation component is very important, at least, in the case of the Franklin Mountains; therefore, our study went beyond a classical stressstrain tensor inversion adding information of the fault rotation in Franklin Mountains.