1 Introduction
In Mexico, as well as in many countries of the world, enterprises seek to be competitive by eliminating their waste and reducing their costs. To achieve this, one of the methodologies that has shown to be successful is the lean manufacturing, where tools are used, such as: Kaizen, Kanban, Single-minute Exchange of Dies (SMED), Six Sigma, Value Stream Mapping (VSM), 5'S, Total Quality Management (TQM), Theory of Constraints, Total Productive Maintenance, Administration Visual, Poka Yoke, etc. to maximize the value string [1, 2].
The procedure of Lean Manufacturing is to select a product (or family) and study the process of manufacturing, using diagrams of operations, flow, travel and build a map of the current value chain (VSM) to identify waste; according to the type of waste, the appropriate tool is selected to eliminate or decrease it. Knowing which the ideal situation of production is, the future VSM is elaborated to implement the selected tools and achieve the goals set [3, 4].
Among the most frequently problems found in the productive systems, we have the waiting times and unnecessary transport, which may have different causes. In our case we will deal with the problem of waiting times, movements and unnecessary transport due to inspection activities. For example, in the punching industry, the manufacture of covers for coolers requires two processes of punching, each of them involves a dimensional inspection for the release of the first part. The inspection operation requires a time of 6 minutes (µ= 6 min) on average, and a tour of 54 m from the puncher to the inspection area and vice versa.
The proposed solution to this type of problem is to implement a vision system for inspection in the same place of production (on site), which operates as a Poka Yoke. This technique allows you to prevent any defective product to go on to the next operation, with which you can have a 100% inspection without the intervention of the human being [5].
The variable to control was the surface roughness of metal parts, as it is considered an important variable in several manufacturing processes; such is the case of the processes of machining and surface finish, where a test of roughness can take from a few hours to days if the tests have to be sent to the certified laboratories.
The objective of this work was to obtain a series of patterns that could link the surface roughness with the Fractal Dimension of the same and use the regression curves to predict the value of the roughness of any other piece in the range of test.
2 Related Works
Some related works whit surface finish of the pieces, the quality parameters are very important, especially for many industrial processes, such friction, contact deformation, heat, electric current conduction, sealing of contact joints, adhesion of coatings and Positional accuracy. The surface finish can be measured in two ways: contact and non-contact methods. Contact methods involve dragging a pencil across the surface; These instruments are called profilometers and have the disadvantage, that they scratch the surface of the piece and mistakes can be made by the user since it requires the calibration of the device to be able to perform the measurement [6].
Non-contact methods include: interferometry, digital holography, confocal microscopy, focus variation, structured illumination, electrical capacitance, electron microscopy and photogrammetry. Within the latter, the measurement of surface roughness by artificial vision can be considered a Method Non-Destructive (MND) that does not require contact to inspect the piece. In this area of MND there are advances such as: In the structure and properties of the three-dimensional world that are tried to deduce in artificial vision include not only geometrical properties (sizes, shapes, location of objects, etc.), but also properties of the material (colors, finishes, composition, etc.), and the luminosity or darkness of the surfaces, using one or more color or monochromatic images [7].
The use of vision systems for inspection and / or selection is being very useful in the solution of problems such as the control of waste, where some data indicate that 70% of it is only used on one occasion and the that 45% is buried or burned. [8], propose an Intelligent Waste Separator (IWS) using a multimedia processor, which processes images to select and separate waste with automatic learning.
It is very common to measure the surface roughness in CNC machined parts by visual methods and compare them with conventional values, contact techniques such as; the arithmetic mean of the roughness (Ra) and spacing between peaks of the midline (Rsm), [9]. Additionally, the characterization can be done with 3D walls [10], and the use of neural networks [11].
In general, texture analysis techniques can be grouped into three large classes: spectral, structural and statistical. Spectral techniques are based on the autocorrelation function of a region or on the power distribution in the frequency domain to detect texture periodicities. Structural techniques describe texture by using pattern primitives accompanied by certain placement rules. Statistical approaches extract, what are called, descriptors of texture characteristics based on histograms of the region of interest (ROI), their extensions and their moments. These descriptors are used to measure the contrast, granularity and coarseness of the image [12].
Several investigations have been carried out to inspect the roughness of the surface based on computer vision technology, an example is the use of the Gray Level Co-occurrence Matrix (GLCM). Another case where the surface roughness of parts manufactured by Fast Prototyping using thermoplastics (ABS) for layer deposition of the fused material using sectioned light vision systems is studied, it has been found that the results are comparable with the traditional method of profilometry for estimate the arithmetic mean of the roughness (Ra) with the benefits of vision inspection. It is mentioned that the most important process variables affecting the finish of the surface are the thickness of the layer and the construction orientation [13].
For the detection of low contrast defects the application of the Wavelet Transform was found under various lighting conditions. In this method, the uneven background was eliminated by the Sobel operation. Then, the low-pass filter and non-linear improvements were used to eliminate the interference and improve the target in the sub-bands produced by Wavelet Transform. As the result shows, the proposed method achieves an accuracy rate of 92.86% in the detection of several surface defects [14].
Among the optical techniques found to measure surface roughness, it uses the analysis of mottle patterns (Speckle), using the combined effects of mottle and scattering phenomena. It was found that there is a strong relationship between the parameters of the bright and dark regions and Ra obtained with the traditional method, especially in the range of λ < Ra <2λ where λ is the wavelength of the He-Ne laser. Although it is a relative method, it has a great potential to be used for measurement and automation in process due to the simplicity of the optical system used [15].
On the other hand, speaking of the techniques that use the fractal dimension as a measure of the roughness, we find in [16], that they suggest the calculation of the Fractal Dimension as a measure of the Texture and Roughness of an image, especially as a measure of the noise present in the image. [17], studies different engineering surfaces and highlights their self-related behavior at different scales. Roughness parameters and material properties have a significant influence on the static and dynamic properties of a rough surface. [18], generate a fractal surface using the modified Weierstrass-Mandelbrot function of two variables in MATLAB and it is imported into ANSYS to construct a finite element model and determine the dynamic characteristics of the surface. A study of the methods used to extract the fractal dimension of surfaces and their applicability to the characterization of them, is presented in [19], where the problem of self-similarity that occurs is also analyzed at different scales.
It is important to mention that industrial processes are expensive in terms of time, money and customer satisfaction. Global economic pressures have gradually led companies to improve these processes to be more competitive. As a result, the demand for intelligent visual inspection systems aimed at guaranteeing high quality in production lines is increasing [20].
3 Techniques for the Measurement of the Surface Roughness
The surface finish is very important in many practical applications, as the surface finish changes the tribology of contact and is decisive in superficial adhesion processes, wear, lubrication and systems of coating. This, in turn, influences the resistance to corrosion, fatigue, affluence and limits the life of the product [21, 22].
A first classification of the measurement techniques of the surface roughness can be made as techniques of contact and those that do not require it. In the first one you use a feeler in the form of a needle whose tip radius defines its resolution (Stylus Profilometry) where, height are obtained through sampling profiles in a standard length, subsequently are averaged and parameters of roughness are calculated, such as: the Arithmetic Mean deviation of the profile with respect to the middle line of the basic length (Ra: ISO 4287, DIN 4768), the maximum Roughness (Rmax, DIN 4768) that represents the highest value of the roughness isolated in the length of evaluation, the root square mean (RQ), the Middle Roughness (Rz, DIN 4768) which is the arithmetic mean of 5 successive values along the basic length.
It is also common to report the standard deviation and the uncertainty of the measurement, however these techniques have the problem that can only be applied to relatively flat surfaces and that can scratch the surfaces of soft materials. Other alternatives are mechanical techniques as the vibration measurement with accelerometers to estimate the parameters of roughness [23].
Among the techniques without contact, we find the optical techniques that use lighting laser (polarized and consistent light) on interferometric arrangements and those that use scattered light reflection. In the first case we found techniques such as white light interferometry (white light interferometer), the method of laser light scattering (scattered laser light method), the method of distribution of intensity of stains of far-field (far-field speckle intensity distribution).
In the second case, it is only the reflection of the light scattered in different orientations [24].
The measurement of the roughness is a problem of multiscale and frequently uses electronic microscopy to obtain the test images at the micro scale, among them: the Scanning Electron Microscope (SEM), the Scanning Tunnelling Microscope (STM) or the Atomic Force Microscope (AFM), although classic metallographic microscopes could be used [25].
4 Image Processing Techniques
The process of inspection by vision may be characterized by 4 steps, that is: Capturing the Image, Image Analysis, Getting Results and Determine the system action (pass or fail) [5].
After the capture of the image, it is necessary to improve the quality of the same and the errors of distortion depending on the type of analysis desired. For this purpose, there are some operations of pre-processing such as: morphological, subtraction and filtering [26, 27].
For the analysis of the image, several methods have been developed, which seek to characterize the texture of images, for example methods based on processing in the frequency domain, the method of random mosaics, methods of spatial dependence of gray levels, methods based on the matrix of autocorrelation, methods based on the matrix of co-occurrence, experimental designs (DOE), designs of Taguchi, the comparison of Trukey-Kramer, the use of artificial neural networks to build models of behavior between input variables and the output [28], and a variety of structural methods [21].
However, when you want to measure the roughness, it should be taken into account that the profile contains two components, the long wave (wiggle) and the micro roughness (shortwave) that are used to separate the procedures of low pass filtering and high pass [25]. For detection of defects based on the texture, approaches can be divided into four categories: statistic, structural, based on filters and based on patterns [29, 30].
The distribution of Wigner-Ville (WVD) is a representation in space-phase that presents a higher resolution in time-frequency that for example the Short-Time Fourier Transform and which is defined as the Fast Fourier Transform (FFT) of the autocorrelation function dependent on time [31]:
where R t (t, τ) is the autocorrelation function dependent on time of the signal s(t) defined by:
The WVD has the following marginal properties in the time domain (or space) and frequency respectively, which prove to be very useful:
Figure 1a shows the spectrogram of the sound "Hola" and 1b shows the distribution of WVD.
5 Calculation of the Fractal Dimension
The fractal dimension D, has been employed in different fields of engineering, among them on the mechanics of soils; where the study of maximum effort of cut plays a very important role in the fracture of rocks, to calculate this parameter it is needed to estimate the normal stress, the roughness coefficient of the union (JRC), the strength of union of the wall and the friction angle. The value of JRC is often estimated by visual comparison of a set of 10 standard patterns.
In this study, we found a large variation between the equations proposed, mainly due to the little information used in the estimation of the models and the inconsistencies in the calculation of D. The methods used for the calculation of D were: the method of compass-walking, box-counting, updated h-L, Higuchi, Hurst, Power Spectral Density [32, 33, 34].
In the area of biomaterials, some parameters of texture of titanium alloys have been studied, such as the index of roughness, the heterogeneity of the image, the distribution of the length of runs, the fractal dimension and have been correlated with the results obtained from profilometers of contact. In terms of the techniques used to determine the fractal dimension in this study, we found the so-called techniques of skyscrapers and blanket [35].
In the analysis of mammographic images with noise, a method was proposed for estimating the fractal dimension in 3D, modelling it as a fractional brownian motion and using the Spectral Power Density of Fourier and its correlation with the roughness. It has been found that an increase in the noise of the image increases its fractal dimension [36, 37]. In our study, we will use the counting method of boxes (box-counting), taking into account some of the recommendations of the method to avoid excessive variations:
where N (d) is the number of boxes of linear size d necessary to cover a set of data distributed in a two-dimensional plane. Introducing the constant C and arranging the equation in the form:
In practice, to measure D one counts the number of boxes of linear size d needed to cover the set on a range of values of d; and trace the logarithm of n(d) on the vertical axis against the logarithm of d on the horizontal axis. If the set is in fact a fractal, this trace will follow a straight line with a negative slope equal -D. To get points that are evenly spaced on the log-log scale, it is better to choose boxes of size d that follow a geometric progression (d = 1, 2, 4, 8,.), instead of using an arithmetic progression. The method requires minimizing the number of boxes N (d) for any size and orientation, it is recommended to do a sweep between 0 and 90º with small increments of Δθ to each box of size d. Additionally, it is recommended to discard the ends of the log-log graph where the slope tends to zero.
6 Materials and Methods
6.1 Vision System
The vision system consists of an intelligent camera (Smart Camera) NI 1722 with a monochrome CCD image sensor of 640 x 480 pixels, 400 MHz PowerPC processor, optically isolated digital I/O and dual Gigabit Ethernet, programmable with the LabView Real-Time Module or configurable with Vision Builder AI. In addition, it requires a 15 pin USB cable, a source of power, a terminal connection and a lens Computar of 12 mm 1:1.4, 2/3.
6.2 Lighting System
We employed two types of lighting: the first by a LED lamp (POWER LED) of cool white light E27 127 V 3W (1000 K). The second by a LED-BAR of 82x16 Red color of 24V-3mm-3L. Both systems, Vision and Lighting attached to two articulated arms with movement in the 3 axes and the possibility of 360º rotation. The type of lighting was of clear field at 15, 45 and 75º angle of incidence with respect to the horizontal (Figure 2).
6.3 Preparation of Specimens
The specimens used were of steel 4140 of 3.8 x 3.5 x 1 cm, prepared with the technique of metallographic roughing, which consists in using silicon carbide sandpaper of numbers 80, 120, 180 and 360. 4 specimens were prepared, the first with sandpaper 80 (P1), the second with sandpaper 120 (P2), the third with sandpaper 180 (P3) and the fourth with sandpaper 360 (P4).
The technique consists of sanding the specimen in a single direction to remove any marks in a different direction; the process repeats making 90 degree turns until you get lines in a single direction.
Table 1 describes the nomenclature for the identification of specimens. Angles of incidence: 15, 45 and 75 degrees.
Table 1 Nomenclature for the identification of specimens
| Specimens | Description |
|---|---|
| P1 LBF 15G L8 |
Specimen 1 corresponding to a slab with sandpaper 80, illuminated with white light (LB) after the filtering process (F) to an incidence angle of 15 degrees, L8 represents the line or row sampled. |
| P2 LRF 45G L32 |
Specimen 2 corresponding to a slab with sandpaper 120, illuminated with red led light (LR) after the filtering process (F) to an incidence angle of 45 degrees, L32 represents the line or row sampled. |
Note: sources of illumination: White LED Light (LB) and Red LED Light (LR). Three angles of incidence: 15, 45 and 75 degrees.
6.4 Acquisition of Images
The acquisition of images was done with the software Measurement and Automatization Labview. The resolution of the images was 640 x 480 pixels with a depth of 8-bit grayscale (format *.png). Once acquired, images were cropped with the software Paint to a size of 200 x 100 pixels with a depth of 32 bits, so that it was necessary to convert them back to 8 bits with the function IMAQ Cast Image of Vision and Motion of Labview. Figure 3 shows the images of the measuring specimen 1 (a, b and c and illuminated with white LED light at 15, 45 and 75º respectively, d, e and f lit with red LED light at 15, 45 and 75º).
6.5 Image Processing
The pre-processing of images consisted of two operations, a low pass filtering (IMAQ LowPass) which calculates the variance of each pixel with its neighbors and if the variation is greater than a specified percentage, then its value is replaced by the average of its neighbors (in this case it is used a percentage of 40% with a Kernel of 3 x 3).
The following operation was a convolution with the function IMAQ Convolute of Vision and
Motion, which represents a linear filter to highlight features in the image depending on the Kernel used, in this case size 3 x 3 whose components were: [1 1 1; 1 5 1; 1 1 1].
The results of these operations are presented in Figure 4, for the case of the measuring specimen 1 in the different test conditions.
6.6 Distribution of Intensities
To perform an analysis of the distribution of intensities, we first selected a region of interest (ROI) of 200 x 100 pixels in the central part of the test piece, then 5 rows at random were taken in each specimen and these were established as the basis for the analysis of the other specimens, the rows selected were: 8, 32, 47, 76 and 91. Figure 5 shows the pattern of intensities for the rows mentioned above in the range of 0 to 50 pixels, and Figure 6 shows a comparison between the pixels filtered with respect to the originals for the total length of 200 pixels.
6.7 Measurement of the Roughness with Contact Profilometer
The Roughness was measured with a contact profilometer Mitutoyo SURFTEST model SV-400, under the norm ISO 4287:1997. There were 7 distributed measurements in the area of the test piece, perpendicular to the scratches (Figure 7). The length of sampling was of 2.5 mm by 5 segments to give a total of 12.5 mm in length of evaluation.
The averaged test results are shown in Table 2. Ra is the Arithmetic Mean deviation of the profile, Rq is the root square mean of the heights, Rz is the arithmetic average of the heights between two lines parallel to the center line (these lines are set between the highest peak and the lowest valley of equidistant segments), and Ry is the value of the Z height maximum.
Table 2 Roughness parameters with Profilometer of contact. (STD, Standard Deviation)
| No | Ra(µm) | Rq(µm) | Rz(µm) | Ry(µm) | ||||
| MED | STD | MED | STD | MED | STD | MED | STD | |
| 1 | 2.41 | 0.11 | 3.11 | 0.15 | 14.3 | 0.65 | 19.7 | 1.56 |
| 2 | 2.04 | 0.2 | 2.61 | 0.25 | 12.2 | 1.13 | 14.5 | 1.35 |
| 3 | 1.24 | 0.09 | 1.59 | 0.12 | 7.96 | 0.74 | 10.5 | 1.17 |
| 4 | 0.33 | 0.03 | 0.42 | 0.03 | 2.31 | 0.13 | 2.93 | 0.15 |
6.8 Correlation between Lines
The aim of this section is to evaluate if the roughness profiles between the different lines of the same test piece follow the same pattern or are correlated. With this purpose, the cross-correlation between pairs of lines in the region of interest (ROI) is evaluated. The analysis was conducted using the software Minitab 14.0, comparing the intensities of each pixel in the corresponding line. Figure 8 shows the dispersion of the data from line 8 against the line 32 and Table 3 presents the Pearson coefficient for each combination to test specimen 1, illuminated with White LED light.
Table 3 Pearson correlation coefficient, specimen 1, white light
| LINE | L8 | L32 | L47 | L76 |
| L32 | 0.376 | - | - | - |
| L47 | 0.342 | 0.528 | - | - |
| L76 | 0.155 | 0.103 | 0.284 | - |
| L91 | 0.03 | 0.042 | 0.193 | 0.407 |
Figure 9 and Table 4 correspond to the same measuring specimen 1, illuminated with Red LED light.
6.9 Wigner-Ville Transform
Taking as a basis the intensity profile of each row (Figure 10), we proceeded to obtain the Wigner-Ville transform using a program developed in LabView 15.0. After reading the previously filtered row, we get the transformation, where the vertical axis represents frequency (Hz) and the horizontal axis the space (Figure 11). The projection in frequency represents the Power Spectral Density.
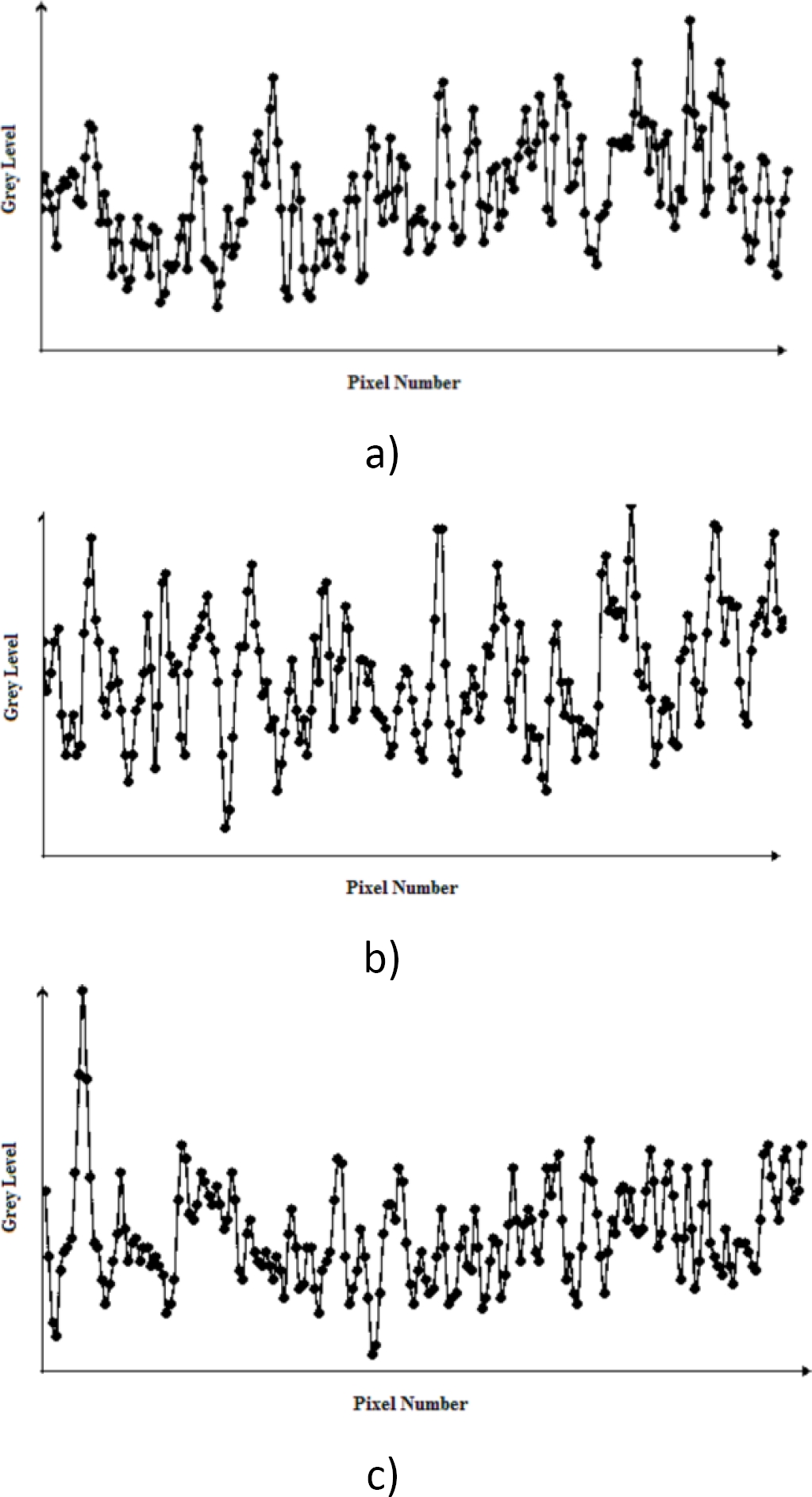
Fig. 10. Intensity profile of the specimen 1, a) row 8 to 15o, b) 45º and c) 75o degrees of incidence angle (Grey Level Vs No Pixel)
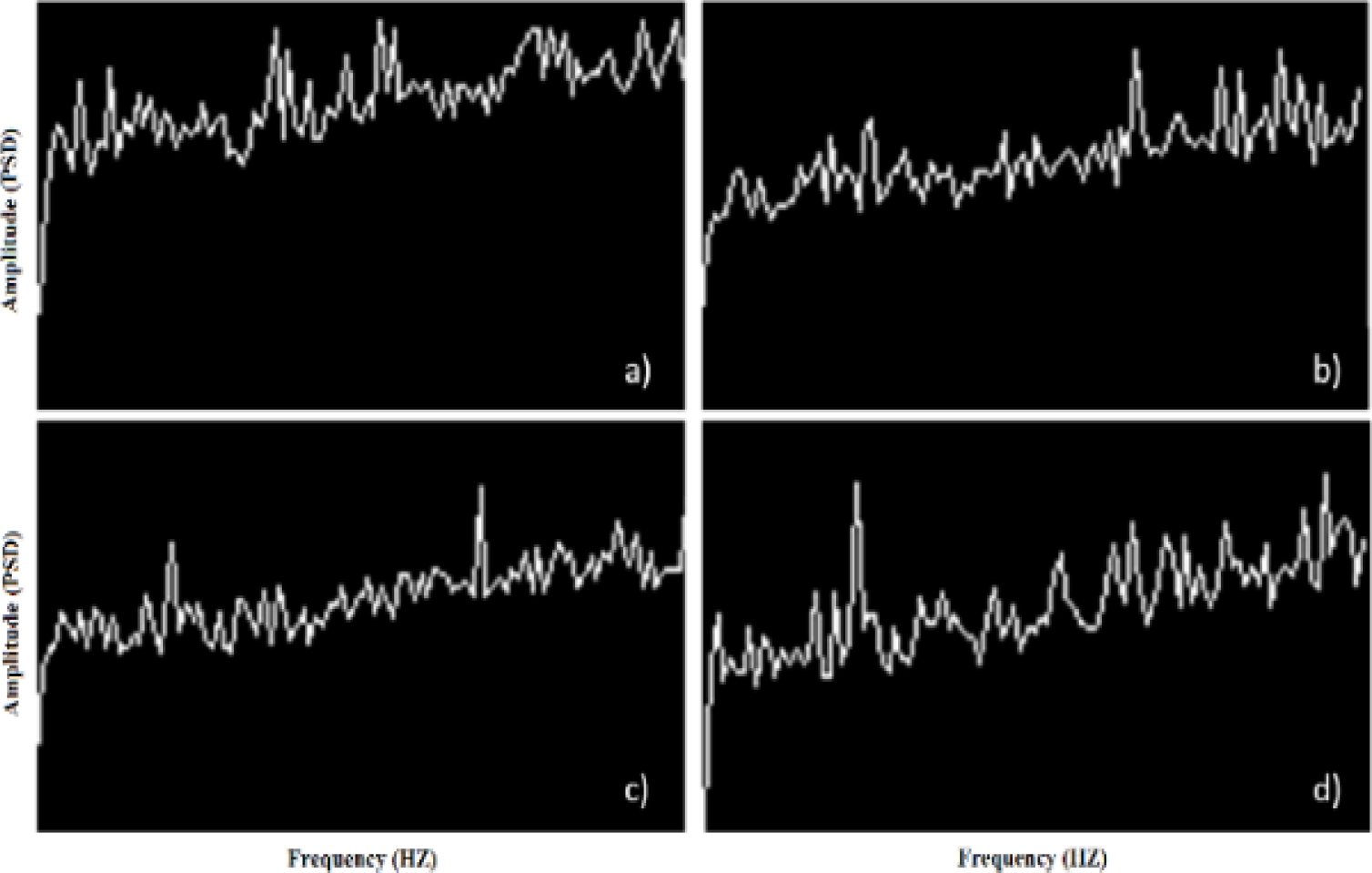
Fig. 11. Distribution of Wigner-Ville and its projection in frequency spectrum (power) for line 8 of the specimen 1
Once processed each of the rows of the different test specimens, we proceeded to save the images of the power spectrum in monochrome format (*.bmp). Figure 12 shows the spectrum of power of the measuring specimen 1 in a) L8, b) L32, c) L47 and d) L76.
6.10 Calculation of the fractal dimension of the intensities spectrum
For the calculation of the Fractal Dimension we used Beniot v1.3 software and the method of counting boxes described by the equation 12. To perform the tests we set out the following parameters: length of the larger box 68 pixels, reduction coefficient of box size equal to 1.3, number of boxes 17, rotation angle equal to 15º. The average results for the spectra of power (Fig. 12) are shown in table 5 for the 4 specimens in the three angles of incidence. There are two cases: the first of them using White LED Light (LB) and in the second case was used Red LED Light (LR).
Table 5 Fractal Dimension average spectrum of Power with respect to the angle of incidence
| No | 15 | 45 | 75 | |||
|---|---|---|---|---|---|---|
| LB | LR | LB | LR | LB | LR | |
| 1 | 1.22 | 1.225 | 1.197 | 1.228 | 1.197 | 1.184 |
| 2 | 1.202 | 1.234 | 1.202 | 1.226 | 1.202 | 1.219 |
| 3 | 1.223 | 1.218 | 1.208 | 1.211 | 1.211 | 1.218 |
| 4 | 1.201 | 1.19 | 1.2 | 1.222 | 1.21 | 1.219 |
As in the case of power spectrum, for the calculation of the Fractal Dimension of the spectrum of intensities (Figure 10), the following parameters were used in the software Beniot: length of the larger box 68 pixels, reduction coefficient 1.3, number of boxes 17, rotation angle equal to 15º. The results are presented in table 6.
7 Results and Discussion
7.1 Acquisition and Image Filtering
In regard to the acquisition of images, we found the formation of bright dots product of constructive interference areas of maximum intensity, which represent peaks atypical in the patterns that have to be attenuated in the filtering.
The filtering process softens the presence of these bright points as can be seen in the patterns of intensity of Figure 4. However, in some cases, the filtering is not sufficient and the elimination of these points is partial as can be seen in the measuring specimen illuminated with red LED light and a tilt angle of 75 degrees (Figure 4f).
The comparison of the intensity profile before and after filtering allows us to decrease the influence of bright spots, for example, for the measuring specimen 1 and row 8, illuminated with white LED light we find less variation between the intensities from a range of 178 to 62 (gray levels).
7.2 Correlation between Lines
With regard to the test of correlation between lines, in Table 3 you can appreciate a low correlation, for example, between line 8 and 32 of the measuring specimen 1, illuminated with white LED light, has a correlation coefficient of 0.376 or 37.6% which is one of the highest values obtained, in contrast with 0.03 of line 8 with line 91. In the case of lighting with red LED light the results are similar (Table 4), so we can conclude that there is not a significant improvement with the use of the red LED light and patterns are poorly correlated.
7.3 Roughness and Fractal Dimension
With regard to the roughness Ra and the fractal dimension D (Table 5), the power spectrum, we didn’t find any type of pattern dealing with both variables for the two types of lighting used. However, when you perform the same procedure to the intensity profiles (Figure 10), you get a good correlation between both variables for the different angles of incidence (Figure 13 and 14).
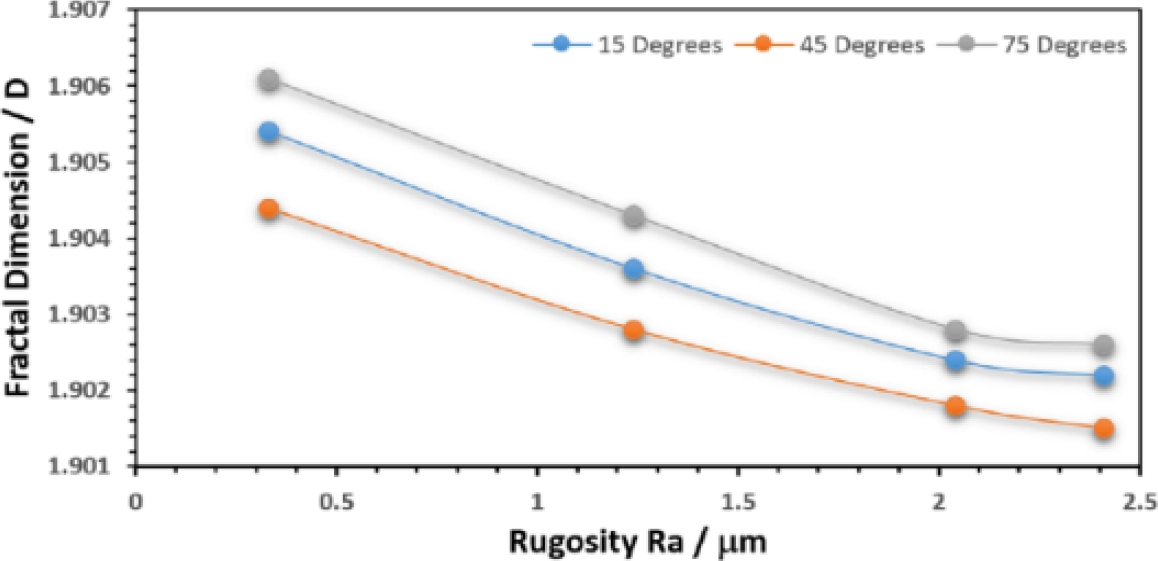
Fig. 13. Fractal Dimension for different finishes as a function of the angle of incidence with white led light as a source of enlightenment
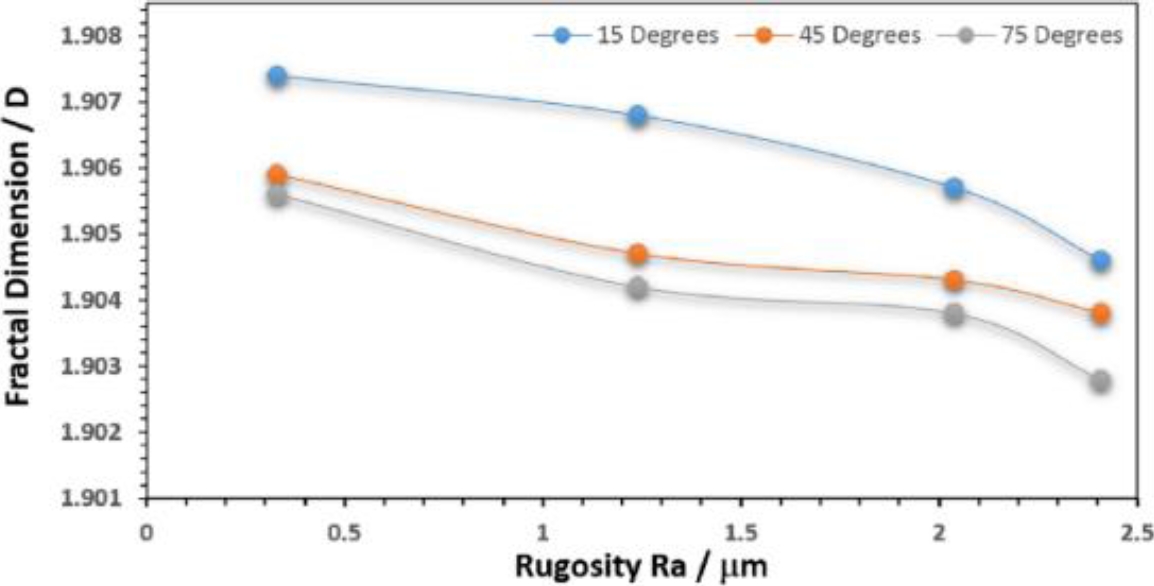
Fig. 14. Dimension for different finishes as a function of the angle of incidence with red led light as a source of enlightenment
Table 8 shows the setting of the data with linear regression, it can be seen that, in general, the setting is good for each position, having a maximum error of 4.1%. However, as it is well known, we can achieve a greater accuracy by the regression of a greater degree.
Table 7 Comparison of intensities, before and after the filtering. (Specimen 1, Line 8)
| Parameter | Line 8 | |
|---|---|---|
| Original (levels of gray) |
Filtered (levels of gray) |
|
| MAX | 216 | 120 |
| MIN | 39 | 59 |
| MED | 84 | 83 |
| STD | 21 | 12 |
| R | 178 | 62 |
Table 8 Adjustment of data with linear regression (θ = Incidence angle)
| Lighting Type | θ | Regression Equation | R-Sq | P |
|---|---|---|---|---|
| White light | 15 | R = 1183 - 621*D | 97.8 | 0.011 |
| 45 | R = 1334 - 700*D | 98.4 | 0.008 | |
| 75 | R = 1077 - 565*D | 98.5 | 0.008 | |
| Red light | 15 | R = 1366 - 716*D | 92 | 0.041 |
| 45 | R = 1931- 1013*D | 96.6 | 0.017 | |
| 75 | R = 1475- 774*D | 94.6 | 0.027 |
7.4 Estimate of the Roughness by Means of the Fractal Dimension
In order to employ the linear regression curves shown in Table 8, we prepared a specimen with a finish equivalent to the sandpaper 240, and after digitizing and obtain their spectrometer of intensity for the same rows sampled, we proceeded to calculate its average fractal dimension, giving us a value of D = 1.9056.
This value and the regression equation for red led light at 45º angle of incidence (Ra = 1931 - 1013*D) allowed us to estimate the roughness of this part in Ra = 0.6272 µm with an error estimate of 1.7%.
7.5 Contributions
Compared with other methods of measuring surface roughness without contact, our methodology does not required any kind of coherent lighting, nor special wavelengths, nor does it require the formation of interference phenomena in complicated interferometers. An important advantage of the method is that the comparison could be made at different scales since the surfaces studied can be considered as self-similar. The main disadvantage is that it requires the elaboration of a series of reference standards under standardized test conditions in order to make the comparisons. However, once the reference standards have been elaborated, the tests are simple and efficient in terms of time and computational resources.
8 Conclusions
We tested the correlation between the surface roughness (Ra) and the Fractal Dimension (D) for two light sources (White LED light and red LED light) and three angles of incidence (15, 45 and 75º), using two techniques: (a) the power spectrum of the distribution of Wigner-Ville and (b) the Spectrum of intensities filtering.
No significant differences were found between both types of lighting, however, the increased intensity was achieved at an incidence angle of 45º with white light.
The results show a greater correlation between surface roughness (Ra) and the Fractal Dimension (D) for the spectrum of intensity that for the Power Spectrum. With these results it is possible to adjust linear regression curves or higher grade to predict the surface roughness of a product with minor errors to the standard of 5 per cent. The estimate will be valid for the test conditions in which an adjustment of the system new patterns should be generated to calibrate the system to new conditions. It is recommended to expand the number of specimens of different finishes to count with standards that cover a wider range.











 nueva página del texto (beta)
nueva página del texto (beta)












