2.1 Discrete Petri Nets

Definition 2.1 A (discrete) Petri net is the 4-tuple N = (P, T, Pre, Post) where P and T are finite disjoint sets of places and transitions, respectively. Pre and Post are |P| × |T| Pre - and Post-incidence matrices, where Pre(i, j) > 0 (resp. Post(i, j) > 0) if there is an arc going from t_j to p_i (resp. going from p_i to t_j), otherwise Pre(i, j) = 0 (resp. Post(i, j) = 0).

Definition 2.2 A (discrete) Petri net system is the pair Q = (N, M) where N is a Petri net and M:P→N∪0 is the marking function assigning zero or a natural number to each place. The marking is also represented as a column vector M, such that its i - th element is equal to M(p_i ), named the tokens residing into p_i. M₀ denotes the initial marking distribution.

A transition t∈T is said enabled at the marking M∈NP iff M≥Prep,t, the occurrence or firing of an enabled transition leads to a new marking distribution M'∈NP that can be computed by using M'=M+CP,t=M+C∙et where C = Post - Pre is named the incidence matrix, and e_t denotes the t - th elementary vector (e_t (k) = 1 if k = t, otherwise e_t (k) = 0).

2.2 Continuous and Timed Continuous Petri Nets

Definition 2.3 A continuous Petri Net (ContPN) is a pair ContPN = (N, m₀) where N = (P, T, Pre, Post) is a Petri net (PN) and m0∈R+∪0P is the initial marking.

The evolution rule is different from the discrete PN case. In continuous PN's the firing is not restricted to be integer. A transition t_i in a ContPN is enabled at mif∀ pj∈•ti,mpi>0 ; and its enabling degree is defined as enabti, m=minpj∈⋅timpjPrepj,ti . The firing of t_i in a certain positive amount α≤enabti,m leads to a new marking m'=m+αCP,ti, where C = Post - Pre is computed as in the discrete case.

If m is reachable from m₀ by firing the finite sequence σ of enabled transitions, then m=m0+Cσ→ is named the fundamental Eq. where σ→∈R+⋃0T is the firing count vector, i.e σ→tj; is the cumulative amount of firings of t_j in the sequence σ.

Definition 2.4 A timed continuous Petri net (TCPN) is a time-driven continuous-state system described by the tuple (N, λ, m₀) where (N, m₀) is a continuous PN and the vector λ∈R+⋃0Trepresents the transitions rates determining the temporal evolution of the system.

Transitions fire according to certain speed, which generally is a function of the transition rates and the current marking. Such function depends on the semantics associated to the transitions. Under the infinite server semantics ^[23] the flow through a transition t_i (the transition firing speed) is defined as the product of its rate, λ_i , and enab(t_i , m ), the instantaneous enabling of the transition, i.e., fim=λienabti,m=λiminpj∈•timpjPrepj,ti (through the rest of this paper, for the sake of simplicity the flow through a transition t_i is denoted as f_i ).

The firing rate matrix is denoted by Λ=diagλ1,…,λT . For the flow to be well defined, every continuous transition must have at least one input place, hence in the following we will assume ∀t∈T,t•≥1 . The "min" in the above definition leads to the concept of configuration.

A configuration of a TCPN at m is a set of arcs (p_i , t_j ) such that p_i provides the minimum ratio mp/Prep,ti; among the places p∈•ti at the given marking m. We say that p_i constrains t_j for each arc (p_i , t_j ) in the configuration. A configuration matrix is defined for each configuration as follows:

The flow through the transitions can be written in vectorial format as fm=ΛΠmm . The dynamical behaviour of a PN system is described by its fundamental equation:

In order to apply a control action to (2), a term u such that 0 ≤ u_i ≤ f_i (m) is added to every transition t_i to indicate that its flow can be reduced. Thus the controlled flow of transition t_i becomes w_i= f_i– u_i. Then, the forced state equation is:

2.3 System Definition

The task model accepted by this framework follows the three-parameter task model ^([7]), but is extended to include energy consumption parameters. Each periodic real-time task τ_i is described by a quadruplet τ_i : (cc_i , ω_i , d_i , e_i ), where cc_i is the worst-case execution time in cycles, d_i is the deadline, ω_i is the period, and e_i is the task energy consumption.

The set of periodic tasks T=τ1,…,τn are executed on a set of identical processors P=CPU1,…,CPUm with an homogeneous clock frequency F∈F=F1,…,Fmax . The hyper-period is defined as the period equal to the least common multiple of periods H=lcmω1,w2,…,ωn of the n periodic tasks.

A task τ_i executed on a processor at frequency F, requires ci=cciF processor time at every ω_i interval. The system utilization is defined as the fraction of time during which the processor is busy running the task set i.e., U=∑i=1nciωi. Herein we consider that the execution of real-time tasks in the system is preemptable.

3.1 Configuration Module

This module allows the introduction of all the information required by the framework. It is organized in four sections: a) Task definition, b) CPU definition, c) Thermal definition, and d) Scheduler definition. The order in which the information is introduced is irrelevant. The user can resort to default values or turn-off some sections, like the thermal definition.

Fig. 3 PCB reference for thermal definition 

The user should consider signals like CPU temperature, system utilization, energy consumption, (or a subset of them) to design her/his own scheduler. At every time step, the section generates a matrix of size Number of tasks × Number of CPUs, where the ij - th entry represents the allocation of the i - th task to the j - th CPU.

3.2 UUniFast Submodule

The user can opt for the UUniFast algorithm ^([4]) to generate the task set in the configuration stage, indicating the number of tasks to be generated, the system utilization U and a range for the task periods. The output is a feasible real-time task set with random task periods, WCETs, deadlines and consumed energy. UUniFast generates one set of tasks at a time. It allows to stress the scheduler under analysis with different set of tasks.

3.3 Kernel Simulation Module

The Kernel module builds up a global simulation model according to the task set, CPUs, thermal and energy parameters and the selected scheduler, and runs the simulation.

The model represents task, CPU and thermal modules by a set of ordinary differential equations, and generates the signals to/from the scheduler. The scheduler can be represented either as a continuous or a discrete system. Accordingly, the scheduler can be modelled by the paradigm of differential equations or finite automata.

Next subsections describe how to build module's models. Later, we explain how the modules are merged into a global model.

3.3.1 Task Arrival and CPU's Submodule

The TCPN model representing the Task arrival and CPU's Module (Fig. 4) was first introduced in ^[17] and evaluated in ^[16]. Here we present a brief explanation of the TCPN model and the differential equations that represent the behaviour. The task module is composed by places piω, picc and pid and transitions tiω. Places piω, picc and pid represent that task τ_i belongs to the set of tasks, the CPU cycles of task τ_i that are arriving to the system, and the deadline of τ_i , respectively. λiω=1ωi represents the arriving rate of task τ_i.

Fig. 4 Task and CPU TCPN module 

The CPU module is composed of places pi,jbusy, and pjidle, and transitions ti,jalloc, and ti,jexec. The marking in place pi,jbusy represents the amount of task τ_i that was allocated to CPU_j. The marking in place pjidle represents that CPU_j is idle. The firing of transition ti,jalloc represents that task τ_i is being allocated to CPU_j , and the firing of transition ti,jexec represents that task τ_i is being executed by CPU_j.

The differential Eqs. (4) and (5) representing the behaviour of the TCPN in Fig. (4) can be derived considering the following four vectors as the marking and transition vectors, respectively, of the task module, and the marking and transition vectors, respectively, of the CPU module:

and

Eq. (4) models task arrival. mτ describes how task are arriving to the system over time, and ωalloc=ω1alloc1,…ωnalloc1,…,ωnallocm represents the allocation of tasks to CPUs. And Eq. (5) describes how tasks are allocated to CPUs, where m _P represents the reservation of CPUs to the allocated tasks. It is very important to realize that signal w ^alloc must be computed by the scheduler. This signal is an input to the system and indicates when a task must be allocated to a CPU:

3.3.2 Task Execution Module

The task execution module is represented by places pi,jexec depicted in Fig. 4. Considering the vector:

representing the marking of the places of the task execution module (for easily representation mi,jexec=mexecp1,1exec), then the task execution behavior is represented by Eq. (6):

where A _P is built from CpΛpΠpmmp considering only rows corresponding to places pi,jbusy and columns corresponding to transitions ti,jexec; other rows and columns are discarded. Marking mAp considers the marking in places pi,jbusy; other markings are discarded.

The marking of these places represent the amount of task τ_i that is executed by CPU_j. This signal is available for any scheduler.

3.3.3 Thermal Module

This work considers the thermal model presented in ^[17], the model was evaluated under comparison with simulations in ASYS®. This model rewrites the thermal partial differential equation by a set of ordinary thermal differential equations. It is as precise as a Finite Element approach and has the advantage that a state model is derived from the analysis. It also avoids the calibration stages of RC thermal approaches, and only requires the isotropic thermal properties of the materials: density, specif heat capacity and thermal conductivity coefficient.

In this section we present a brief explanation, for a deeper insight please refer to ^[17] and ^[16]. The thermal module is composed of several thermal submodules, representing thermal conduction, convection and heat generation. The arc from transition ti,jexec to place picom1 represents heat generation due to task execution.

Fig. 5 depicts the thermal module. Following the numbering of places and transitions, the temperature behaviour of the system is represented by Eq. (7a):

Fig. 5 Thermal module 

mT is the distribution of temperature over the system elements, ma is the ambient temperature and it is considered constant, and fexec is a variable depending on task allocation and the frequency at which CPUs are executing tasks. CPU temperature is available for scheduling purposes. Temperature depends on the task execution and frequency. In steady state, this is tantamount to say that temperature depends on task allocation ωiallocj and frequency. As mentioned above, these parameters are coded in fexec

At each simulation step, the Thermal model reads the new system state and the ambient temperature to compute the new CPU temperature. The main output signals of the Kernel simulator are the task execution vector ( mexec) and the CPUs temperature ( mT) at each simulation step. The input (output) signals are received (sent) to the Scheduler module in order to obtain a feedback signal for the next step.

3.4 Scheduler Module

The scheduler module allows to select, at configuration time, one of the scheduling policies available in the framework, or any scheduler defined by the user. The TCPN The signals available to the scheduler from other modules are mi,jexec representing the amount of τ_i executed by CPU_j , and mTj the CPU_j temperature. The signals that other modules require from the scheduler are the task allocations signals ωiallocj.

The scheduling policies available in the framework are an RT Global Earliest Deadline First (G-EDF) ^([1]), an RT fluid scheduler (RT-TCPN)^([15]), and an RT thermal-aware fluid scheduler (RT-TCPN Thermal aware) for Dynamic Priority Systems (DPS) ^([16])). The user can define a new scheduler as a continuous or discrete scheduler (Sec.5).

3.4.1 Custom Scheduler

This section describes how to implement a custom schedule. Algorithm 1 provides the executive cycle of the simulator. It includes the scheduler (user defined or pre-programmed one) in line 4.

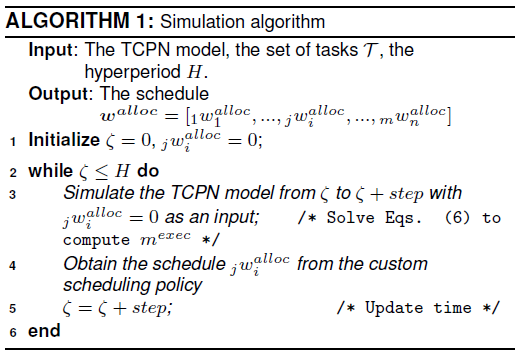
The main input signals, from the simulation environment, that the user might use, are the CPU temperature, executed tasks, current CPU frequency and consumed energy, also the secondary signals mbusy (the CPU state), and all task and CPU parameters are available for scheduling purposes. The output signals that the scheduler module must deliver to the simulation engine are the ωalloc and frequency. It is not needed that all the input/output signals be used by the scheduler; the only mandatory signal that the scheduler must deliver to the system is ωalloc. For presentation purposes, this subsection renames the variables x1=YT CPU temperature, x2=mexec executed tasks, x3=F current CPU frequency and also the secondary signals x4=mbusy.

If the user describes the scheduler as a continuous one, then he/she must write the signal walloc as:

If the user describes the scheduler as a discrete one, then he/she must write the signal ωalloc as:

In both cases, the functions represented by the matrices A_i or function ɸ are computed based on the scheduler objectives and task and CPU parameters, as well as the current state of the system. It is the user responsibility the design of such a functions.

Notice that the simulator is time driven, thus, although in the discrete case the ωalloc signal depends on the event arrival, it is represented as a function of time the make it compatible with the whole simulation.

Finally, once the scheduler is defined, it is integrated to the simulation engine and used at each simulation step.

3.5 Building the Global Model

A full system in the simulation framework consists of a set of tasks, a set of CPUs on a platform, and a scheduler (as an input), represented by separated models. In order to simulate a full system, these models must be gathered into a global model. In the case of a continuous scheduler, the global model is simulated by solving the system:

where M=mT,mP,mTT , and the matrices are:

Ap correspond to the output matrix for task execution and ST represents the temperature output matrix. Thus the output vector Y=mexec,mT contains the task execution and the temperature of each processor. If the thermal module is not selected for simulation the global model is slightly different: vector M will only contain M=mT,mP every matrix (Eq.9 - 11) will lose its last row, and Eq.(9) will also lose its last column, and the output vector Y=mexec will only contain the task execution.

3.6 Results Module

After a simulation run, the Results module generates plots showing the allocation and execution of jobs to CPUs and the CPUs temperature evolution, as in Fig. 10 and Fig. 11, by using the tools and functions contained in MATLAB R2018a®(ie. Heat maps).

5.1 G-EDF

This scheduler implements a global EDF (G-EDF) algorithm. It is a global job-level fixed priority scheduling algorithm for sporadic task systems, which is optimal for implicit-deadline tasks with regard to soft RT constraints ^[2]. Jobs are allocated to CPUs from a single queue. The highest priority is assigned to the job with the earliest absolute deadline. The signal jωialloc must be discrete. At each simulation step the scheduler can be written as: ωalloc=Φmexec. According to the EDF algorithm, the scheduling events are task activations and task completions, the only points at which task preemption can occur. The discrete function Φmexec is implemented by algorithm 2.

5.2 RT-TCPN

RT-TCPN is a scheduler based on the TCPN model presented in ^[15]. It is composed of a global fluid scheduler and the discretization of the fluid scheduler. The fluid schedule computation is limited to every deadline, whereas preemption and context switch occur at every quantum, at which we check the difference between the actual and the expected fluid execution. RT-TCPN obtains a discrete schedule that closely tracks the fluid one ( mexec) by computing a schedule up to the hyperperiod ^([3]).

The algorithm considers the ordered set of all tasks' jobs deadlines to define scheduling intervals, as in deadline partitioning ^([18]). Each task τ_i must be executed ni=Hωi times within the hyperperiod H. Thus every q*w_i where q = 1,...,n_i is a deadline that must be considered in the analysis. These deadlines can be gathered and ordered in the set SDi=sdi1,…,sdini. A general set of deadlines is defined as SD=SD0∪…∪SDT where SD0=0. The elements of SD can be arranged in ascendant order and renamed as SD=sd0,…,sdα, where α is the last deadline. We define the the quantum Q as in ^[15]. The fluid execution FSC=FSCT11,…,FSCTi,…,FSCTnmj is a vector with number of tasks × number of CPUs entries. The signal FSCTij stands for the desired allocation of the i - th task to the j - th CPU at time ζ. This function can be computed as:

where βij is an unknown parameter that represents the number of jobs of task τ_i which are assigned to CPU_j per time unit. This value is used to compute a distributed fluid schedule function that considers temporal constraints, according to an offline stage that solves the following linear programming problem:

The actual execution mi,jexec of τ_i in CPU_j must be equal to FSCTij. In the on-line stage a sliding mode controller yields an output signal jωialloc that is proportional to the error (difference between FSCTiζj and mi,jexec). The formal proof of this controller is given in ^[15]. The scheduler ( ωiallocj) meets all deadlines assuming an infinitesimal share of the CPUs because its fluid nature, ans therefore must be discretized. The discrete scheduler must be written as: Walloc=Φmexec,FSC, where Φmexec,FSC is described by Algorithm 3. The computed discrete schedule Walloc matches the fluid schedule at every deadline sdk∈SD. Since these time points are the deadlines of jobs, then the algorithm ensures that the discrete schedule meets all deadlines of all tasks.

Fig. 8 depicts the scheme of the algorithm implemented in this framework. The dotted box A contains a set of signals that represent the normal behavior of the system. Signal A.1 describes the function FSCTiζj obtained in the off-line stage, and is used as the reference for the on-line stage. In the on-line stage the controller yields an output signal ( ωiallocj, named A.2 in Figure 8). The controller output is integrated by the TCPN model. Signal A.3 describes the output of this model. Finally, the algorithm RT-TCPN uses the difference between mi,jexec (the expected executed amount of τ_i in CPU_j ) and Mi,jexec (the actual executed amount of τ_i in CPU_j ) to compute Wiallocj i.e. the on-line allocation of τ_i to CPU_j at every quantum Q.

Fig. 8 RT-TCPN Scheme 

5.3 RT-TCPN Thermal Aware

The schedule computation in this algorithm encompasses temporal and thermal constraints. The temperature of the chip must be kept under a temperature threshold T_max that depends on system design requirements. The fluid schedule function introduced in ^[3] is extended to include thermal restrictions. This is achieved by considering the steady state of Eq. 7a, i.e. if the schedule is periodic, fluid and evenly distributed over the hyperperiod, then the temperature must reach a steady state. Thermal Eqs. (7a and 7b) can be rewritten as:

AT corresponds to the system matrix, BT is the input matrix, and B'T conforms the matrix associated to the ambient temperature (m_a which is considered constant). These matrices are:

Thus, in a thermal steady state M˙T=0 , MT and YT are respectively renamed as MTss and YTss indicating a system steady state temperature, which can be computed as follows:

The steady state temperature YTssk of CPU_k must be less than or equal to its maximum temperature level i.e., YTssk≤Tmaxk so as not to violate the thermal constraint. In a vectorial form: S'MTss≤Tmax.

The thermal constraint is derived by combining the last expression and Eq. (17).

The task allocation vector ωalloc depends on the unknown parameter βij. These parameters are used to compute the distributed fluid schedule function that considers thermal and temporal constraints, according to the following linear programming problem:

The first constraint is the thermal constraint. The other two constraints are a straightforward extension of the time and CPU utilization used in the RT-TCPN algorithm for the multiprocessor case. The required fluid schedule function FSCTiζj is defined similarly as Eq. (12). The temporal and thermal requirements are accomplished as long as the tasks are executed according to this function. Task execution is represented by variable mi,jexecζ, hence the task execution error is defined as ei,jζ=FSCTiζj-mi,jexecζ . If ei,jζ=0, then tasks are executed at the adequate rate, and the time and thermal constraints are met. Therefore, this error can be kept equal to zero by appropriately selecting ωiallocζj. We propose a sliding mode controller for this purpose. The formal proof for this controller is beyond the scope of this paper. We provide the following key hints, nonetheless.

Considered the sliding surface:

where ω^iallocζj=K2signSi,jζ and signx=1 if x ≥ 0; 0 otherwise.

Figure 9 shows how the implemented algorithm works. It is composed of the off-line and online stages. Based on an LPP, the off-line stage computes the functions FSCTiζj to meet the temporal and thermal constraints. The on-line stage use these functions as the target for task execution. The sliding-mode controller continuously allocates tasks to CPUs to ensure that the task execution tracks the functions FSCTiζj. The dotted box A in figure 9 shows the set of signals that represent the normal behavior of the system. Box B depicts a disturbance, an unexpected behavior of the system such as a CPU detention. Signal B.1 describes the FSCTiζj, as in the normal case. If a CPU detention occurs at time ζ₁, then the difference between FSCTiζj and the actual execution of τ_i in CPU_j starts to increase at this time. Thus the controller output signal ( ωiallocj, named B.2) also starts to increase at time ζ₁. The controller output is integrated by the TCPN model (Eq. 8) producing an output mi,jexec (signal B.3) that is greater than FSCTiζj. Finally, the algorithm RT-TCPN Thermal aware computes Wiallocj, which also increases at time ζ₂. When the CPU resumes at time ζ₂, the controller allocates tasks to CPUs more often than in the normal case, using the CPU idle periods until normal operation is reached at time ζ₃ . Approaches that do not include a continuous controller are not able to recover from CPU detentions or other disturbances that can temporarily stop task execution.

Fig. 9 RT-TCPN Thermal-Aware Scheme