1 Introduction

Mobile robots have been widely studied for decades. Many applications are related to robotic tasks such as navigation, distribution, object and person localization, map construction, space coverage, among others [⁸, ¹⁴]. Due to the environment, mobile robots can be classified as aerial, terrestrial, and underwater [⁵]. Mobile robots can also be wheeled, legged, or tracked, depending on the means of locomotion. Therefore, the design of a robot – from its mechanical configuration to electronic devices and computational resources – depends directly on its application and complexity of the tasks [³, ⁸]. Interestingly, four-legged robots can move on uneven terrains, as opposed to wheeled or tracked robots. Other advantages are the improvement in their mobility, the ability to avoid obstacles, the active suspension, the energy efficiency, and their ability to handle speed [⁸]. But, the analysis, mechanical design, optimization processes, control systems, and dynamic simulations, are of great interest nowadays [⁸].

The use of gripping tools, or simply grippers, in robots is an active area that has the advantage of manipulating and grasping objects. But those carry out some limitations for the robotic systems, such as [⁹]: increase the degrees of freedom, robot dimensions also increase, movements are turned more complex, cost increase, transmission of forces to the rest of the robotic body, and many others. Due to these limitations, some roboticists have moving onto the use of soft materials for the design of gripping tools, known as soft grippers [⁹]. This type of tool makes use of materials with modulus of elasticity of the order of 10⁴-10⁹ considered soft, which allows adaptability of the surfaces and a reduction in the number of actuators required. However, it increases the complexity of its design and mathematical modeling. Regarding the above, gripping design methods, known as synthesis processes, have been proposed the heuristics techniques to optimize the topology and dimensions of soft robotic tools.

Artificial intelligence (AI) has gained visibility in mechanical design and mechanical engineering [², ⁴]. The first efforts of AI-assisted design comprised of rule-based and knowledge reasoning. Those provide a system able to define a product using a description of parameter settings and constraints [¹⁰]. The geometry of products and tools, as well as the use of computer-aided design (CAD) software, are important for the AI reasoning systems [¹⁰]. Computational intelligence, i.e., intelligent optimization, is the most used AI tool in mechanical design [¹, ⁶, ⁷, ¹³]. For example, Datta et al. [⁶] proposed the use of a multi-objective evolutionary optimization algorithm to design a robotic gripper for micro-machining. The authors modeled mathematically a generic gripper, and then, they imposed design constraints as multi-objectives to solve their problem. Bhoskar et al. [¹] reviewed different applications of genetic algorithms (GA) for mechanical engineering design. The work showed AI-assisted design is specific for the product to be designed, and the AI method employed must be shaped accordingly to the type of the end-product. AI has been also implemented for soft gripper design. For example, Runge et al. [¹²] proposed a design framework using GA for soft actuators. This framework consists of design (with parameters) a part of the soft actuator, then optimize it using GA, then evaluate the design with finite element analysis (FEA), and lastly perform a kinematics analysis.

In a previous work [¹¹], the authors designed and implemented a prototype of a four-legged robot inspired in the biomechanics of chameleons, as the one depicted in Figure 1. This robot aims to walk on narrowed surfaces, like beams or pipes, for future applications as rescue and maintenance. So far, the mechanical part and the balance controller have already been implemented. However, the legs slip into the contact surface, and its locomotion performance diminishes considerably. Therefore, a robotic gripper is required (like a prehensile hand) avoiding relative sliding between the legs and the surface.

Fig. 1 Prototype of the chameleon-like robot 

Thus, this paper presents an AI-assisted design using GA of a soft gripper for the chameleon-like robot. The methodology comprises the problem formulation, the setting up of the genetic algorithm (e.g., individual encoding, fitness function, evolutionary operators), and the implementation in co-simulation between a CAD software and the GA solution. In this work, we use a network-attached storage (NAS) server connecting multiple nodes running the GA solution in parallel, to accelerate the process. We present simulation results to validate our approach.

The rest of the paper is organized as follows. Section 2 presents the methodology followed in this work, including the problem formulation and the GA solution. Section 3 describes the implementation of the GA solution and the co-simulation with the CAD software. In Section 4, we present the results. Lastly, Section 5 concludes the work.

2 Methodology

Mobile robots have been widely studied for decades. We propose a methodology based on GA for designing the soft gripper required for the chameleon-like robot. This methodology comprises the following steps: (i) formalize the design problem, (ii) design the GA method for solving the design problem, and (iii) implement the GA system in co-simulation with a CAD software. Figure 2 summarizes the methodology, and the details of the first two steps are given below. The description of the last step is presented in Section 3.

Fig. 2 Methodology implemented for designing the soft robotic gripper using GA 

2.1 Problem Formulation

We require to add a soft gripper at all legs in the robot since they slip into the contact surface. In this work, we restrict the design of a single soft robotic gripper. In general, the final design can be replicated in the four legs.

From the above, the goal of the GA system is to shape a soft gripper with the best grasp as possible when it is actuated. The soft gripper has two main states, as shown in Figure 3. The first state represents the initial position in a release position, while the second state is the final position got after the gripper is actuated (i.e., injecting compressed air). As depicted in Figure 3, the final position is obtained from the deformation of the soft material; but this deformation depends on the initial shape of the gripper and its structure. In that sense, the output of the GA system should be a suitable shape in the initial state that is able to change the shape reaching the final state with the strongest force possible to make the grasp.

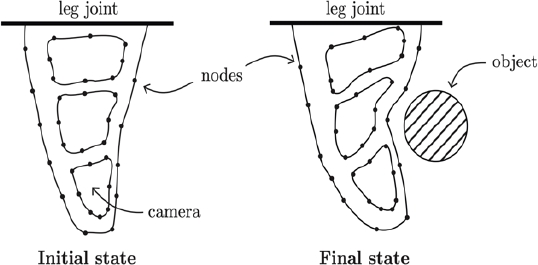
Fig. 3 Main states of the soft robotic gripper: (left) the initial state B(1) before applying compressed air, and (right) the final state B(2) after actuated 

In this work, we restricted the texture of the material unchanged. No modifications to the texture by adding roughness to the material are allowed.

In that sense, the design problem is formulated as follows. Consider a base form B of the gripper. Then, B is parameterized by n nodes defined in three-dimensional (3D) space pi=(xi,yi,zi)∈ℝ3 for all i=1,…,n and assuming a set of constraints C. These constraints impose the minimum and maximum displacements of nodes, the dimensions of the piece, and no cross-points resulting in forbidden bodies.

The nodes shape the initial state of the gripper B(1)={p1(1),…,pn(1)} comprising both the perimeter and the structure. Also, suppose there is an external object O near the gripper. Then, an external force FA is applied to the soft gripper, such that, it reaches the final state B(2)={p1(2),…,pn(2)} and grasps O with contact forces F(2) between the B(2) and O. Thus, the design problem is to find a set of nodes forming B(1) that allows reshaping of nodes forming B(2), by applying FA, and maximizes the forces F(2).

2.2 Genetic Algorithms for Designing the Soft Gripper

We present a GA system to solve the design problem given previously. In general, GA is a popular method in stochastic optimization that can find a near-global solution [¹²]. GA has been found to be a good choice in (multiple) global optimization [¹⁵].

GA works using a population that is a set of individuals representing candidate solutions to an optimization problem. These individuals encode the parameter values in a form of small components called chromosomes. Each individual is evaluated to determine its effectiveness, and the GA uses a fitness function. The latter is a quantitative measure that is used as ranker of individuals in the inner process. GA employs different operators to enrich the exploration and exploitation of candidate solutions in the search space. For instance, it combines individuals using a crossover function to express new individuals. It also provokes small changes in individuals using a mutation function. These operators create a new population that is assuming to be better than the current population. After several number of iterations, called epochs, individuals in a population evolves until a suitable solution to the global optimization problem is reached by the best individual evaluated in the fitness function [¹²].

To solve the design problem, we encode the set of points pi(1) in individuals. We set an initial population of N individuals representing different base forms B(1). The population is, then, evaluated in a fitness function f that promotes individuals with large values of contact forces F(2) and no violations to constraints C. In each epoch, a crossover operation is performed between individuals, and a mutation operator is also applied to all individuals. After a certain number of epochs, the GA returned the best individual evaluated in the fitness function. Algorithm 1 summarizes the GA using for designing the soft robotic gripper. Details are given following.

Algorithm 1 GA for designing the soft robotic gripper 

2.2.1. Individual Encoding

First, we encode the individual as a set of nodes defined in 3D coordinates that parameterizes the base form in the initial state B(1).

In this case, an individual indk, for all k=1,…,N, is the joint positions pi of the set of nodes in their three coordinates, as shown in (1). For simplicity, pi(1)=pi.

indk={p1(1),…,pn(1)}={x1,y1,z1,…,xn,yn,zn}. (1)

We use a binary encoding for the individual. Since the positions are in millimeters and assuming that the maximum position value is not greater than 256 mm, then an 8-bit representation of integer values is enough. Thus, each individual 𝑖𝑛𝑑_𝑘 has length equals to 8(bits)×3(dimensions)×n(nodes).

2.2.2. Fitness Function

We define a fitness function as an evaluation measure of the individuals. The fitness function f evaluates the position of nodes in the initial state such that they can move, by an external force FA, to the positions in the final state and apply large contact forces F(2) between the gripper and a given object. The fitness function f is expressed in (2), where FFEA(2) is the resultant contact force calculated using FEA in the final state B(2) produced by FA with initial position of nodes as encoded in an individual ind, and PC is a positive penalty assigned when a constraint cj∈C is violated.

f(ind)=FFEA(2)(ind)−PC. (2)

In this work, each violated constraint produced a penalty value PC. Three constraints were imposed: a point pi is within the maximum dimensions of the gripper (c1), the whole position of nodes give a well-defined body with no cross-points (c2), and the displacements of all nodes from the initial state to the final state let the gripper well-defined (c3). For convenience, the FEA and the calculation of constraints are done in a CAD software, as described in Section 3.

2.2.3. Crossover and Mutation

Then, two operators over individuals are defined: crossover and mutation. We implement one-point crossover that chooses two individuals and split them into two parts in a random position of the chromosome. The first part of one individual is then concatenated with the last part of the other individual. A crossover operator is performed with probability pco. We use roulette selection to pick individuals for crossover. Furthermore, we implement mutation of individuals that consists of changing a chromosome value by its complement. A chromosome is mutated with probability pmut.

3 Implementation

As noticed, the GA system for designing the soft robotic gripper requires a co-simulation with CAD software. In this regard, we propose to use SolidWorks for calculating the FEA of an individual created by the GA system. Since the procedure is quite time consuming, we decided to implement the whole system in a NAS server to evaluate the fitness function in parallel using a cluster of heterogeneous agents. Figure 4 shows the implementation of the system.

The GA system was implemented in Python with the pyeasyga library. Each time the fitness function f is evaluated, the individual is decoded and the position of nodes in the initial state are sent to SolidWorks. Then, the CAD software receives the positions and renders a 3D model of the base form B(1). To compute the final state, we design the profile of the beam (i.e., object) that the gripper needs to grasp (see Figure 3). Then, a simulation of motion was programmed in SolidWorks. After the gripper gets in contact with the beam, the FEA is computed. Finally, the FEA returns the total contact force FFEA(2) (measured in kg-f/cm² units) and the constraint violations to the GA system.

Fig. 4 Implementation of the GA system in co-simulation with SolidWorks in a NAS server 

The NAS system comprises of five heterogeneous agents: three cloud-based services and one NVIDIA Jetson Nano computer. The whole system sees a unique co-simulation between Python and SolidWorks. Thus, there is transparent on how the co-simulation is implemented. Specifically, the evaluation of f is done in parallel to accelerate the whole process.

4 Results and Discussion

We use the NAS-based co-simulation system to design the soft robotic gripper. For the GA system, we manually set up the following parameters: the population size N=115, the maximum number of epochs max_epochs=25, the crossover probability pco=0.5, the mutation probability pmut=0.1, and the penalty value PC=0.1. We run the experiment six times to see the variability of the output grippers designed by the GA system. Figure 5 summarizes the final grippers found during the six simulations.

Fig. 5 Final soft robotic grippers designed by the GA system, from results of six times of runs 

As shown in Figure 5, the output grippers have similarities. For example, from results 1–4, the left profile is thicker than the right side (the contact surface with an object); this gives more room for the compressed air and the gripper can bend it more. In contrast, results 5 and 6 are weaker in the left side showing more stress (cyan color), but it is not crucial for the design. Another similar characteristic is the cavity formed up the contact area. This cavity jams the profile of the beam, arising more contact force (green color). Furthermore, result 2 is the biggest gripper generated among the others.

About the cameras that give structure to the gripper, there is a relationship of shapes between the middle and the last cameras. If the middle camera has a large surface in the contact area, then the last camera is tiny and oval (results 1–3). However, if the middle camera has almost no surface in the contact area, then the last camera is large and forms a triangle-like shape (results 4–6).

The latter results come with a larger contact surface. These observations give us insights about that results 4–6 are better for our application. To this end, the fitness function evaluation among these results ranks result 5 as the best design. The results sorted are: 5, 6, 4, 3, 1, and 2, from best to worst.

Figure 6 shows the sequence from the initial state B(1) to the final state B(2) of the result 5, as an example of the deformation of the soft robotic gripper designed by the GA system.

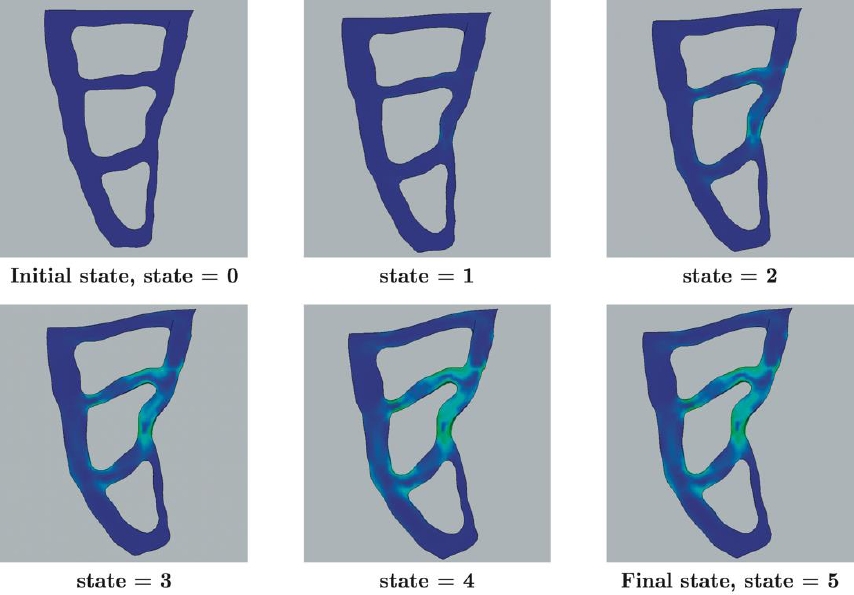
Fig. 6 Sequence of deformation of the designed soft robotic gripper from result 5. The sequence comprises from the initial state B(1) to the final state B(2) 

This sequence shows that the initial position of nodes provides the right motion of the soft gripper. It means that the deformation makes to the side where the object must be grasped. The sequence also reveals that the shape of the middle camera allows a proper bending of the gripper, while the last camera almost remains in the same shape during the whole trajectory. The latter is important because this camera provides a strong structure to the tip of the gripper.

To this end, we prepared a silicone mold in negative to the gripper obtained as result 5. This mold will be used in the next steps to prototype the soft gripper into the robot. Until now, the simulation of the silicone mold can be observed in Figure 7. This gripper will be replicated to the four legs of the robot.

Fig. 7 Simulation of the silicone mold that will be used for creating the soft gripper of the robot prototype in the future. 

As shown, the GA system was able to design a soft robotic gripper with the requirements and constraints imposed. In terms of the GA, the implementation required to use a NAS-based system to co-simulate the candidate solution, given by the GA, into a CAD software. This simulation required the performance of a FEA each time the fitness function is evaluated, so the simulation is time-consuming. In addition, we run the experiment six times, and we observed that the results are similar among them, but differences were also found.

The main strength of our methodology is that we designed a suitable soft gripper. But it also has some limitations. In this methodology, we tuned the hyper-parameters of the GA manually; the crossover and mutation operators create individuals that violate the constraints, increasing the time for selecting proper individuals; and the fitness function did not consider intermediate states of the gripper deformation that might have more information to get better designs. Thus, improvements to the methodology will be considered for further experimentation.

5 Conclusions

This paper proposed an AI-assisted design, using GA, of a soft gripper for a bioinspired robot. The methodology comprised the problem formulation, the settings of the GA, and the implementation in a NAS-based system for co-simulation between the GA module and the CAD software.

As shown in the results, the GA system properly designed a soft robotic gripper. For experimentation, we run the GA six times, getting similar results in all of them. From the best soft gripper design, we analyzed the sequence of deformation to determine some characteristics in the structure and the contact forces applied. Lastly, we used this design to build a silicone mold for future manufacturing of the soft grippers to all the legs of the robot.

For future work, we will implement the grippers into the robot prototype. In addition, we will improve our methodology to obtain better designs of the soft gripper. In these improvements, we will consider other ways to find proper values to the hyper-parameters of the GA, study other crossover and mutation operators to generate valid individuals and add more information of the sequence of deformation into the fitness function.