1 Introduction
The control of flow separation has been studied since the performance of aerodynamic bodies is affected by the separation. Passive such as dimples and vortex generator, are chosen by its simplicity.
Although it cannot control the flow well situations that are beyond design limits of the device and under dynamic conditions.
On the other hand, active flow control devices have also been investigated and developed in order to overcome the shortcomings of passive flow control devices.
Active flow control techniques like blowing and suction have been studied for more than 50 years, and its effectiveness for a separated flow control has been demonstrated.
But these devices have serious drawbacks due to its complexity and the addition of weight which limits its application.
The periodic excitation, a type of active flow control, have contributed to better understand the separation phenomena, and the development of linear stability theory for shear flows had led to the invention of modern active flow control techniques.
Modern flow control techniques using unsteady actuation require even less actuator power than the steady boundary layer control techniques (of the order of
In recent years to overcome the disadvantages of more traditional flow control devices, pulsed micro-jets [11], synthetic jets and Single Dielectric Barrier Discharge (SDBD) plasma actuator are being investigated. Plasma actuators have different applications in aerodynamics, they have been used to reattach the flow over an airfoil as did by Corke [3].
Huang [9] used them to control the separation in low-pressure turbine blades. Other use is to enhance the performance of wind as studied by Greenblatt [7]. In the present work a technique to simulate a plasma actuator for flow control over an airfoil is presented.
The plasma actuator is implemented by means of a body force source term which is directly introduced into the momentum equation. We studied the flow control in a NACA 0015 airfoil with a SDBD plasma actuator at Reynolds number (Re) of
Plasma actuators have great advantages, such as responsivity, low weight, a simple structure, and a low energy consumption. For this work we will focus the results to show the developed technique capability to be used for flow control and it is emphasized the usage of
An SDBD actuator is a device that through an electrical discharge ionizes the air and by the acceleration of the ions by the electromagnetic forces there is a transfer of momentum inside the boundary layer which induces a jet inside the boundary layer, as seen in schematic diagram of Fig. 1, this causes a decrease and delay of the flow separation.
To simulate the propulsive force from the actuator, several computational models that seeks to accurately reproduce the properties of plasma, such as ion formation rate, and particle collisions. These models entails an increase in the computational cost making them unpractical for engineering applications.
The other type has an engineering focus such as the Suzen model [15] or Shyy model [14], these are based on the principle that the body force is directly proportional to the product of the charge density by the electric field.
However, these models have some drawbacks such as the electrodes should be strictly modeled into the domain since the thickness and position of these are necessary for the equations that determine the electric field, in addition to adding electric equations to the solver.
To avoid that disadvantages Dörr and Kloker [4] have used a technique in which the body forces are modeled as source terms. Kloker states that a SDBD can be modeled as a body force parallel to the wall. In the work done by Sato [13] he used the Suzen model to calculate the magnitude of the force that is applied as a source term directly in the momentum equation.
Plasma actuators have two modes of operation, they can work in a continuous mode in which it is continually activated, or through pulses as in the so-called burst mode. It has been proved that an actuator operating in the burst mode is more energy efficient, than an actuator in the continuous mode. [16, 13, 1, 6].
2 Modeling of the Flow and the Actuator
2.1 Flow Modeling
The flow field around the plasma actuator an the airfoil is described by the Reynolds-averaged Navier–Stokes equations (RANS) equations. In this work consider the flow as incompressible, the change in temperature is neglected, as it is known most of the energy that the plasma actuator consumes is transformed into kinetic energy, this leads to the required equations are the continuity and momentum equations:
where
This model uses a
It is a model capable of capturing separation. The
where
The turbulent viscosity
2.2 Actuator Modeling
As mentioned in the previous subsection, the body forces provided by the plasma actuator are modeled by adding the source term, fb into the momentum equation (2).
In this work we used the Kloker model [4] to obtain the the plasma extent over the wall, by using the equation (7), we obtained that the body force extends from the wall up to a distance of 0.003x/c, in the Fig. 2 the extension of body force is shown:
Then the magnitude of the body force was selected from the results obtained by Hofkens [8] in which he determined the strength of a plasma actuator from velocity field data.
To obtain the unsteadiness of the body force, we multiply the body forces by the square of the sine function, as can be seen in the equation (8):
where
The burst mode is produced by a signal generated by the multiplication of low-frequency square signal with a high-frequency sinusoidal base signal, that way the actuation is periodically switched on and off. In Fig. 3 is shown a schematic of the burst mode, and in Fig. 4 a plot of the signal generated by a burst frequency of 15 Hz and a base frequency of 2 kHz is shown.
The burst mode is controlled by the burst ratio equation (9), and the burst frequency. If the burst ratio is equal to one (BR=1.0) the actuator is operating in the continuous mode. The burst actuation has the advantage for separation control, as some periodic excitation controls, the boundary layer receptivity, acoustic disturbances, coherent vortex shedding:
where the active time for each pulse
The dimensionless base frequency
2.3 Computational Cases
The cases were divided in two setups in the first setup, the actuator was located at 3% (x/c=0.03) and 10% (x/c=0.01) of the chord length from the leading edge, then BR=1.0 and the
See Table 2 for the first setup, and Table 3 for the second setup of cases. The maximum force magnitude was
where
Table 1 Mesh properties
| Parameter | Mesh 1 | Mesh 2 | Mesh 3 |
| nodes | 629,700 | 775,500 | 104,7340 |
| cells | 313,650 | 386,400 | 522,000 |
| max aspect ratio | 306.773 | 309.543 | 277.867 |
| max non-orthogonality | 29.171 | 29.5681 | 29.6446 |
| max skewness | 0.45114 | 0.45267 | 0.45037 |
Table 2 Cases for the study of the position of the actuator
| Position | BR | ||||||
| 0.03x/c | Continuous | - | 660 | 2.0 kHz | 1.0 | ||
| 0.10x/c | Continuous | - | 660 | 2.0 kHz | 1.0 |
Table 3 Cases for the study of the frequency of the actuator
| BR | ||||||
| 16 | 1 | 3 Hz | 660 | 2.0 kHz | 0.5 | |
| 16 | 5 | 15 Hz | 660 | 2.0 kHz | 0.5 | |
| 16 | 15 | 45 Hz | 660 | 2.0 kHz | 0.5 | |
| 16 | Continuous | - | 660 | 2.0 | 1.0 |
This gives us a momentum coefficient
3 Computational Setting Up
3.1 Numerical Grid
A structured C-type mesh was generated with the OpenFOAM utility
The
To use
To define the coordinates of the airfoil an
By executing the command
Steady state simulations with same initial and boundary conditions were performed for a range of angles of attack from
3.2 OpenFOAM Configuration
The simulations were carried out in the open-source software OpenFOAM. The actuator is simulated in OpenFOAM as force source term, that is added into the momentum equation. There are two ways of adding the force one involves modifying a solver and the other trough
The body force can not be directly added by modifying a solver and adding the body terms in the momentum equation, since by doing this the body force will be applied to the whole domain as for example a gravitational force, as for this work is required that the force is applied only into a specific region, then we used the
To generate the cell zone the
In
We used a rotated box because since the length of the actuator is small which allows the cell zone to adjust to the wall slope change along the airfoil chord. execute the function the command
The actuator is simulated in OpenFOAM as force source term, that is generated with the
A typical
Then constants for the actuator frequency and strart time are defined:
After the force term is defined as a
For the boundary conditions, a condition of type
A boundary condition of type
To ensure a two-dimensional flow, a boundary condition of type
The keyword
— time: backward,
— gradient: cellMDLimited Gauss linear 0.5,
— divergence: Gauss linearUpwind,
— laplacian: Gauss linear limited 1.0,
— interpolation: linear.
The linear solver was GAMG (geometric-algebraic multi-grid) for the symmetric matrix p, and for the asymmetric matrices U,k,omega and nuTilda a
The time step for the simulations was controlled by means of maximum Coruant number of 0.5, it was used and adaptable time step function to reduce the computation time for each simulation.
The simulations were solved in parallel on distributed processors. OpenFoam uses the public domain openMPI implementation of the standard message passing interface (MPI).
The decomposition method used was
4 Results
The simulations of a NACA 0015 airfoil were performed at Re of
The Fig. 9 shows the velocity field when the actuator is inactive (off), and active (on). It is observed that when the actuator is inactive there is a flow separation zone that goes from the trailing edge to distance near 0.6x/c.
When the actuator is active the flow remains attached, the separation zone is reduced, its only appreciated near the trailing edge, in this case the actuator was placed at 0.03x/c. The flow reattachment its more visible when the airfoil is stalled as seen in the Fig. 10, in this case the actuator is able to take out the airfoil from the stall.
As mentioned in the section 1 plasma actuators add momentum to the flow, this induces a jet within the boundary layer, the simulations proved to be able to replicate the boundary layer jet as seen in Fig. 11. The
With the actuator off the pressure peak is almost vanished, and consequently the lift. When the actuator is on there is significant low pressure recovery near the trailing edge. Fig. 14 shows the enhancement of the airfoil as the
When the actuator is on there is a significant reduction of the drag at high angles of attack from a range from
It is observed that independent of the burst ratio frequency the
Fig. 17 shows the temporal evolution of the velocity in a half period (T=0.5), measured in a point 3 mm downwind the actuator and 1 mm over the wall, from this plot the effect of the burst mode as the actuator is being activated and deactivated, for example for a
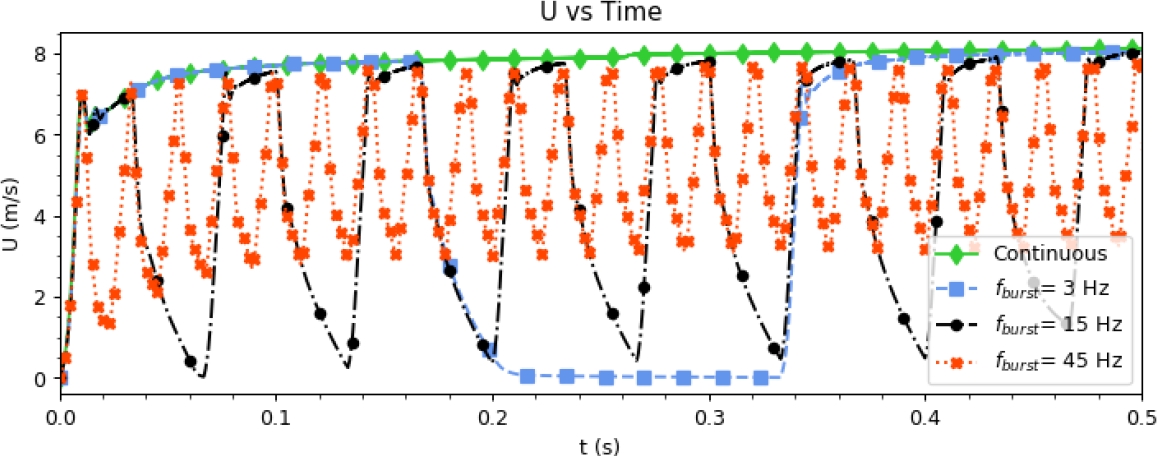
Fig. 17 Evolution of the velocity in a point at x= 3 mm downwind the actuator and z=1 mm over the wall,
4.1 Validation
To validate the technique implemented in this work, were performed at a Re of
It is observed that the simulations
5 Conclusion and Future Work
The results of the CFD analysis technique applied to an airfoil section showed us a great potential and high capabilities to simulate and evaluate the Kloker plasma-fluid model for a Single Dielectric-Barrier Discharge and the
This technique is cheap, fast, effective and free of the software licenses to simulate the performance of any plasma solver to attach the boundary layer after the stall or bubble separation in a wing section.
The numerical algorithm called pimpleFoam with nCorrector is one of the most stable setups for this case and the accuracy of the results strongly depends on the choice of grid size, y-plus, wall function and discretization scheme.
The tested cases showed that when the actuator its closer to the separation region produces a higher increase of the
Plasma actuator has great advantages, such as responsivity, low weight, a simple structure, and a low energy consumption.
Reason enough, for this paper who provides detailed data support for subsequent numerical and experimental studies on airfoil cases with a 3D flow and more complex turbulence models.











 nueva página del texto (beta)
nueva página del texto (beta)























