1 Introduction
Data fusion systems are applied widely in the sensor networks, robot systems, video-processing, images-processing and intelligent design systems. The emergence of new sensors, advanced processing methods and improved processing hardware allow researchers to develop the data fusion.
The data fusion is proposed for the military purposes, target trajectory tracking and medical engineering [8]. This data fusion is a process that the obtained information from various sensors systems and states observers are combined to provide the drawing accurate decision precision.
The problem of data fusion for multi-sensor systems is based on the speed of the samples with equal sampling rates resulting in relatively simple data integration with limited application. The input variables for the data fusion systems include sensor information, command signals and previous data. The data fusion problem provides a powerful tool for information and draws decision [24].
Therefore, a combination of data analysis from multiple sensors to increase knowledge of the system is challenging task [16]. The data fusion of multi-sensor measurements is a challenging task as providing an estimation of the states vector over a sensor. Among the many techniques for multi-sensor data fusion, artificial intelligence, pattern recognition and statistical estimations are of the most importance of these attitudes [20].
There exist particular problems in the data fusion like the presence of non-proportional sensors, the emission of signals and noise environments [12].
The most fundamental fusion characteristics are the transfer functions of the dynamic model among the observed states and the multi-sensor parameters and the decision or inference. A quantitative assessment of the data fusion systems is obtained usually through Monte Carlo simulations or analysis techniques of covariance error [11]. The combination of multiple sensors is a process of combining information that is gathered from different sensors and takes place at three levels of data, features, and decision making.
In the composition of data levels, all unfeasible data measured by multiple sensors is combined directly from a factor to generate useful information. Consequently, the selection of the described model depends on the function of the sensor combination and there exist no predefined model for data fusion.
In this article, Kalman filter is utilized for the continuous linear models of sensors in categorizing the state sequence and constitute with two dynamic models of sensors in the data fusion problem. This article is organized as follows. Different methods of data fusion are introduced in section 2. Examples of data fusion application in the different systems are surveyed in section 3. Experimental example of data fusion method with using an extended Kalman filter approach is utilized in section 4 and the article is concluded in section 5.
2 Different Methods of Data Fusion
2.1 Data Fusion by Applying Kalman Filter
Kalman filtering is widely applied in applications like optimization, estimation methods, filtering ability, measurement uncertainties, and mathematical models in the modern techniques of pursuing multi-sensory objectives [5]. The Kalman filter is a data recursive algorithm that estimates the uncertain system dynamics.
This algorithm is implemented subject to two processes of prediction of states based on the mathematical model and state correction based on the measured data from the sensors.
In practice, the Kalman filter is implemented with the assumptions that the systems is linearized by a linear dynamic model and is usually incompatible with the modeling error caused by the linearization. All the system dynamics and noise processes are specified exactly in the Kalman filter.
The combination of measured values is preferable to the state-vector combination when data fusion multi-sensor is based on the Kalman filter. The state-vector data fusion methods will be effective when the Kalman filter is stable, which limits the practical applications of data fusion methods; consequently, in many algorithms, the information is optimized through the Kalman filter.
The extended Kalman filter combines the measured data from multiple sensors to provide optimal results in the accumulated error terms, functionality, and frequency response. If this model is fully adjusted, the residue tends to be zero between the predicted and actual bode and converge within a bounded range. The extended Kalman filter equations are presented as follows:
where
where,
The general block-diagram of the data fusion is proposed through an extended Kalman filter method as Figure 1. In this article, the values of angular velocities are calculated through an extended Kalman filter for two gyroscope sensors with different transfer function models.
2.2 Data Fusion Using the Support Vector Machine (SVM)
The divergence of the modeling errors is very important in the Kalman filter transfer functions. All the system state variables or estimation errors matrices are unrealistically dimmed and the Kalman filter loses its efficiency when the measured values do not provide enough information to be estimated. Moreover, the estimates can be applied to solve the modeling errors due to the divergence.
This issue increases the complexity of the Kalman filter, and can not guarantee that all the unstable states of the transfer function are the real models. The data fusion problem is addressed by the SVM algorithm that formulates the decisions to separate the different regions [25]. The support vector machine (SVM)-based multi-sensor data-processing system extracts features from the measured data [1].
A non-linear SVM provided through the kernel function when the obtaining data from the sensors does not change linearly becomes necessary [4]. A sensory combination method for assessing the physical activity of human beings based on SVM, which is an effective in the reducing system changes and, in particular, when the obtained data is augmented from the sensors to the combination transfer function model is proposed.
A hybrid method for categorizing the error signal based on the combination of sensor data through a SVM is proposed and a short-term Fourier transform transformation (STFT) technique is utilized. One of the advantages of SVM is the low number of parameters necessary for computation by the user where most of the parameters are determined by the internal algorithm. Therefore, the computational complexity of the SVM is subject to the number of data points relative to the system dimension.
2.3 Data Fusion for the Noise Systems
The data fusion problem is a challenging issue due to the existence of inaccurate and misleading data, contradictory data, data correlation, operation time, data dimensions and noise data [26].
The combination of inaccurate dates like noise can have an adverse effects on the parameters estimation of transfer function. The common filtering techniques, based on the Kalman filters, rely on Gaussian noise and linear models that are not appropriate for the noise environments, accordingly, decisions are made on the basis of the hypotheses given where a decision test is made to ignore unreliable sensors [9].
3 Examples of Data Fusion Application in the Distinctive Systems
Data fusion is usually run in the form of a matrix method that separates the data sets from the higher-order matrices [27]. To assess the efficiency of the data combination in a random manner, some coefficients are changed to determine the effectiveness of the proposed method in the determining measurement parameters from inaccurate data. A new method for thecoefficients estimation is presented by applying a combination of two primary acceleration and pressure sensors in [23].
A high-level sensor combination is applied to get information from an unreachable sensors [7]. An interpolation data combination operator weighed by a sample of specific coefficients is suggested such that this method is not limited to clustering, classification, pattern identification, group decision methods, and data combinations [2].
An integrated algorithm is devised to combine the data fusion to produce parameters estimates some of the qualitative parameters in [6]. For many applications, information is provided by special sensors that are incomplete, inaccurate, and invalid [3].
The problem of data combinations for system instability, multi-speed, and multi-sensor linear systems are assessed in [22], where, the transfer function model is only specified for the best sampling rate, and is developed to combine the data from multi-sensor systems through the Kalman filter. A multi-sensor combination algorithm is proposed for the surgical surveillance with a human body that combines devices and explanatory data at a single moment [21].
4 An Experimental Example of the Data Fusion Method Using an Extended Kalman Filter Method
In this article, the data fusion is applied on some multiple gyroscope sensors to estimate the state variables. One of the most common factors in the experimental systems is the control and evaluation of angular velocities, which is measured by the gyroscope sensors [17]. To measure the angular velocities, the gyroscope sensors are modeled with a suggested second order transfer function, that is expressed as follows [18, 14]:
where, parameters
In order to evaluate the problem as best as possible, two different variances are determined based on the gyroscope sensors. As a result, the equations of the proposed model are presented for the gyroscope simulation with different systems damping coefficients as follows:
The Gaussian noise with zero mean and different variances 0.1 and 0.2 are augmented to evaluate the effects of the proposed gyroscope transfer function model, the measured values and the applied noise [13, 19].
The suggested block-diagram of data fusion between the two gyroscope sensors in the measuring angular velocities is drawn as Figure 2. In this section, three different data fusion structures are proposed for the measuring angular velocities between the two gyroscope sensors and their results are compared:
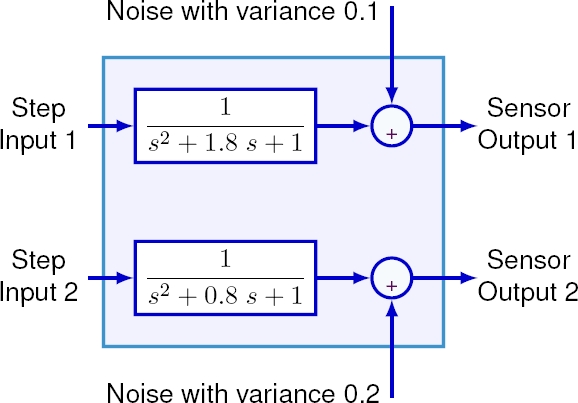
Fig. 2 The suggested block-diagram for the data fusion between two gyroscope sensors in the measuring angular velocities
The suggested extended Kalman filter algorithm is applied to combine the obtained data from two gyroscope sensors according to the proposed data fusion structures.
The step response of the gyroscope sensors and the estimated transfer function coefficients through an extended Kalman filter are shown in Figures 3 and 4, respectively.
The covariances in a steady state of the data-fusion methods are evaluated by the changing process covariance to provide the estimated coefficients for drawing accurate decision precision.
The estimated transfer functions are calculated from an extended filter Kalman for the measuring angular velocities between the two gyroscope sensors as follows:
The results of the data combination for the measured values in the various transfer
function models are tabulated in Table 1,
where, the terms
Table 1 The comparison scenario between different modes of the gyroscope sensors data fusion
| States | C1 | |
| S1 | 0.071 | 0.65 |
| S2 | 0.056 | 0.51 |
| DF1 | 0.073 | 0.25 |
| DF2 | 0.022 | 0.38 |
| DF3 | 0.021 | 0.29 |
The error variance
Table 2 The comparison between Kalman filter coefficients and errors variance for the different noise covariance
| Q | var | |
| 0.07 | 0.01580 | |
| 0.23 | 0.04370 | |
| 0.65 | 0.01317 | |
| 0.17 | 0.35820 | |
| 0.03 | 0.73220 |
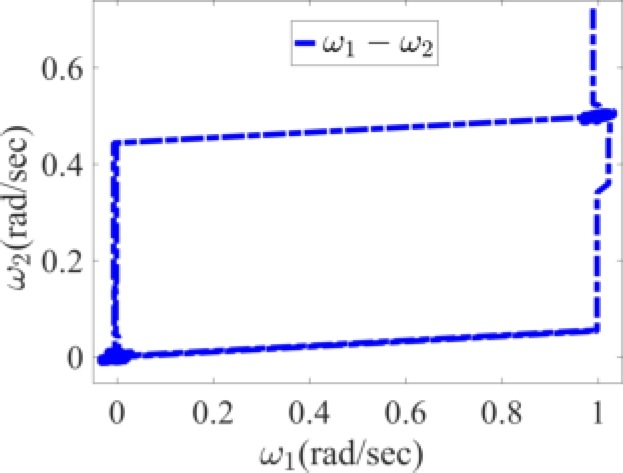
Fig. 5 The variation of the estimated transfer function for obtaining angular velocities between two gyroscope sensors
The numerical results indicate that the errors variance and extended Kalman filter coefficients increase for the convergence rate with increasing in the noise covariance of different states.
By increasing the number of gyroscope sensors in the multi-sensor transfer function models, algorithms based on ordinary Kalman filters will lead to more calculations and low resistance.
The consecutive pulse response of gyroscope sensors and the calculated coefficients by an extended Kalman filter approach are illustrated for the obtaining angular velocities in spite of the applied noise in Figures 6-7, respectively.
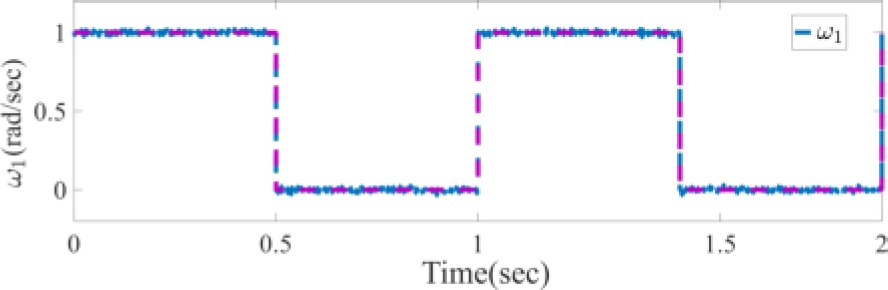
Fig. 6 The consecutive pulse response of gyroscope sensors through extended Kalman filter in spite of the applied noise
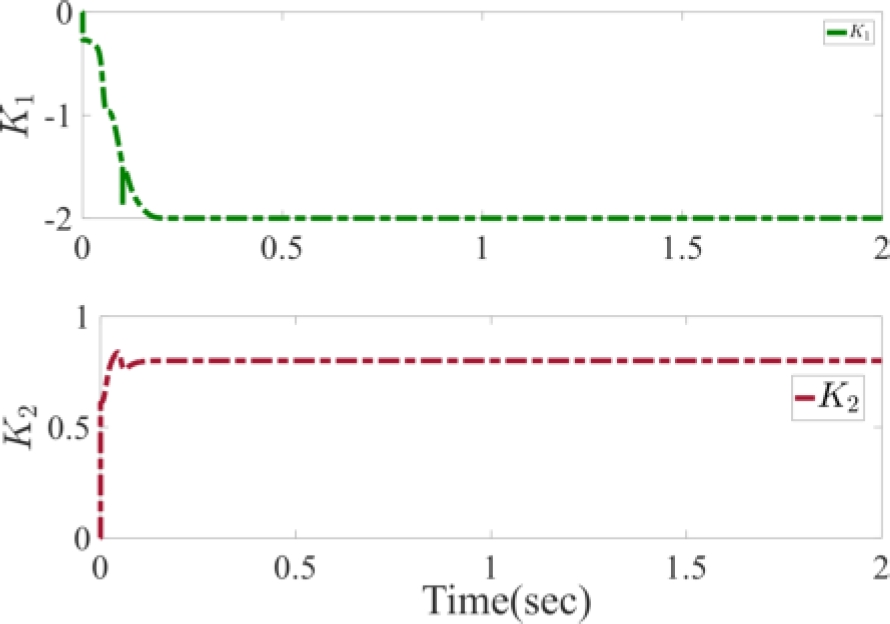
Fig. 7 The calculated coefficients by an extended Kalman filter approach for the obtaining angular velocities
The evaluation of the tables 1 and 2, show that the combination of data between the two gyroscope sensors will have more flexibility in relation to the proposed structures than a sensor.
The comparison scenario between extended Kalman filtering coefficients
From the obtained data fusion of the gyroscope multi sensors for different responses in tables 1 and 2, the selection of the described transfer functions of the dynamic models is correctly selected.
Consequently, the combined data is more accurate and reliable than the received data from a single sensor and all these features are combined for the logical decisions.
The combination of decision-making is the highest level of composition that incorporates the combination of different sensors and implies the importance of classifying the composition for the best result.
5 Conclusion and Future Work
The results of the various experiments indicate that the modeling and analyzing based on the data fusion and multi-sensors are of a higher degree than modeling based on a sensor system.
The data analysis is subjected to the applied technique, the numbers of sensors and the working conditions. Despite all the proper Kalman filtering capabilities for data fusion, the great numbers of modes are necessary for accurate estimation with no ability to determine the parameters changes.
To measure the angular velocities, the gyroscope sensors are modeled with a suggested second order transfer function and the parameters of these suggested models are calculated through an extended Kalman filter. These obtained models are investigated in the three structures of data fusion to provide the drawing accurate decision.
Consequently, the collection and analysis of data by obtaining multi-sensor sources can be applied to each system that is more accurate and in-depth than the obtained data results from a single sensor.











 nueva página del texto (beta)
nueva página del texto (beta)





