Cálculo de la mortalidad en la población del estado de Puebla, usando las Tablas modelo de la ONU y el método de Ricard Genova

 

Mortality calculation of the State of Puebla population using the model tables from UN and the Genova Ricard method

 

Gerardo Martínez-Guzmán, Mario Mauricio Bustillo-Díaz, Rogelio González-Velázquez, Beatriz Bernabé-Loranca, Alejandro Rangel-Huerta, Gabriel Juárez-Díaz, Apolonio Ata-Pérez, Nicolás Quiroz-Hernández Y Rosa María De Lourdes Reyes-Vélez

 

Benemérita Universidad Autónoma de Puebla

 

Artículo recibido el 23 de junio de 2014
Aprobado el 2 de junio de 2015.

 

Resumen

Los estudios en la medición de la mortalidad sirven como indicadores del avance socioeconómico y sanitario. En éstos se observan la evolución y tendencia de los factores de mayor preocupación universal de la humanidad: la salud. la extensión de la vida y la posibilidad de evitar la muerte prematura. Lo anterior está relacionado con diferencias entre grupos sociales y grupos de población según edad y sexo, para identificar el grado de adelanto o atraso en las condiciones de bienestar. Existen diversas metodologías para el cálculo de las Tablas de vida. En este trabajo se utilizará el modelo matemático de Ricard Genova, que usa las tablas modelo propuestas por la ONU para el cálculo de las Tablas de vida. En esta aplicación del método se utilizan datos del estado de Puebla para estudiar el comportamiento de la mortalidad en la población de dicha entidad federativa.

Palabras clave: Modelo de Ricard Genova, esperanza de vida, probabilidad de muerte, probabilidad de supervivencia, tasa de mortalidad, tablas tipo.

 

Abstract

The studies of mortality measurement serve as indicators of socioeconomic and health progress. In these studies the evolution and factor trends of the most universal concern of mankind are observed, such as health, life extension and the possibility of avoiding premature death. This is related to differences between social groups and population groups by age and sex, in order to identify the advancement or backwardness degree in welfare conditions. There are diverse methodologies for the calculation of life tables. In this paper the mathematical model of Ricard Genova employing the model tables proposed by the UN to calculate life tables is used. In this application of method the Puebla State data is used, in order to study the mortality behavior in the population from this state.

Key words: Ricard Genova model, life expectancy, death probability, survival probability, mortality rate, type tables.

 

Introducción

Cuando se institucionalizó la investigación demográfica en 1960 en la Universidad Nacional Autónoma de México y pocos años después en El Colegio de México, se inició la investigación sistemática de la mortalidad a través de métodos más refinados. En 1967 apareció la primera publicación mexicana sobre mortalidad para los años 1930, 1940, 1950 y 1960. A partir de entonces se incrementó notablemente la preocupación por conocer con mayor precisión el comportamiento y tendencias de la mortalidad no sólo a nivel nacional, sino en cada entidad federativa.

Los estudios y la medición de la mortalidad actúan como indicadores del avance socioeconómico y sanitario que observan la evolución y tendencias de los factores de mayor preocupación universal de la humanidad: la salud, la extensión de la vida y la posibilidad de evitar la muerte prematura, que permiten detectar diferencias entre grupos sociales o ámbitos geográficos y grupos de población según edad y sexo, para identificar el grado de adelanto o atraso hacia condiciones de bienestar. Estos estudios ayudan a determinar grupos o regiones objetivo para realizar nuevos programas sanitarios o bien evaluar el éxito de aquellos ya instituidos.

A pesar de que existen diversas metodologías para el cálculo de las Tablas de vida, el modelo matemático de Ricard Genova no ha sido utilizado en México, aunque se manejan las tablas modelo propuestas por la ONU para el cálculo de las Tablas de vida. En este artículo se aplicará el método usando las Tablas de vida modelo desarrolladas por la Naciones Unidas. En esta aplicación se usan datos del estado de Puebla, México, para estudiar el comportamiento de la mortalidad en dicha entidad federativa.

A pesar de que existe información sobre datos de mortalidad en Puebla, existen pocos trabajos sobre la proyección de este importante indicador (CONAPO, 2008). En este trabajo se hace una proyección estadística sobre los índices de mortalidad y de esperanza de vida para la población de la entidad utilizando el método de Ricard Genova (Vinuesa et al., 1997) y las tablas modelo tipo de la ONU (CEPAL/UNFPA/CELADE, 2005), que es una técnica con ciertas variantes respecto a la mencionada.

 

Características generales de la mortalidad

En Demografía el concepto de mortalidad se emplea para expresar la acción de muerte sobre los integrantes de una población (Maldonado, 2005; Livi-Bacci, 1993). La muerte es un riesgo al que toda la población está expuesta durante toda su vida y además es un hecho que ocurre una sola vez a cada persona; estos aspectos hacen que el estudio de la mortalidad sea relativamente más simple que el correspondiente a los otros componentes demográficos como la fecundidad y la migración (Vinuesa et al., 1997).

Un elemento que contribuye a definir la importancia del análisis demográfico de la mortalidad es que los diversos aspectos del comportamiento de esta variable están relacionados con la estructura por edad y sexo, así como la composición por causas de muerte (Alba, 1974). Este elemento es empleado frecuentemente como indicador del estado de salud de la población (CONAPO, 2005, 2008).

 

Tipos de Tablas de mortalidad

A continuación se presentan las diferentes tipos de tablas de mortalidad:

a) Tablas por generaciones y Tablas de momento

Cuando se construyen Tablas de mortalidad por generaciones, se utiliza el principio de seguir una generación o cohorte de personas en el tiempo hasta su completa extinción (Ramírez, 2000: 5). Esto significa que se va siguiendo en el tiempo a la generación de individuos nacidos en un periodo de tiempo determinado (un año por ejemplo), observando cómo los efectos de la muerte (fenómeno que ocurre una sola vez) van disminuyendo el número de sobrevivientes hasta la extinción completa de la cohorte. Realmente este es el principio original de una Tabla de mortalidad.

En el ámbito demográfico, este tipo de acercamiento metodológico es conocido como análisis longitudinal (ONE/CEPD, 2004). Muchas veces se le llama también análisis de flujos poblacionales y siempre está referido a un periodo de tiempo.

La principal ventaja del análisis longitudinal es que permite una mejor interpretación de los fenómenos. Sin embargo, tiene la desventaja de que habría que esperar más de cien años para conocer las condiciones de mortalidad de una generación. Esto quiere decir que los indicadores longitudinales no están diseñados para dar cuenta de lo que está pasando en la actualidad. En el caso de la mortalidad se mezclan condiciones muy diferentes en el tiempo, porque una generación estaría pasando y siendo observada a lo largo de cien años, en los que evidentemente se producen cambios importantes en las condiciones de salud de la población.

Las tablas más usadas son las del momento o de contemporáneos, las cuales también suponen la progresiva eliminación de los efectivos de una generación inicial causada por la mortalidad y la generación es ficticia. Estas tablas se basan en la experiencia de mortalidad observada durante un corto periodo de tiempo (usualmente un año o un promedio de varios años) con una población estimada en el periodo observado (Ortiz, 1999; Mina, 2006). Para el estudio de la mortalidad se forma una cohorte hipotética, la cual se somete a las condiciones de mortalidad de la población en el lapso considerado. En general, cuando se habla de Tablas de mortalidad se está haciendo referencia a este último tipo de tablas.

b) Tablas completas y tablas abreviadas

Las Tablas completas son aquellas en las que se elaboran diferentes funciones para cada año de edad, mientras que en las Tablas abreviadas se calculan las diferentes funciones por grupos de edades (grupos quinquenales). No obstante, dentro del grupo de 0 a 5 años de edad de la mayoría de las Tablas abreviadas se incluyen las diversas funciones por grupos de edades simples, ya que dentro de dicho intervalo la mortalidad varía mucho con la edad y esta información resulta de gran utilidad para el estudio de las condiciones de vida de la población infantil y juvenil, principalmente para la planificación de la salud.

Como es de esperarse, la construcción de las Tablas de mortalidad se basa en la teoría de la probabilidad. Se parte de la probabilidad de muerte, que se calcula mediante la relación entre los eventos ocurridos (las muertes ocurridas en una población a una determinada edad) y la población (de esa edad) sujeta al riesgo de la ocurrencia del mencionado evento.

 

Tablas tipo

Las Tablas tipo, conocidas también como Tablas de vida modelo, son estructuras de mortalidad por edad que no responden a ninguna población concreta. Se obtienen tomando en cuenta las características de un gran número de Tablas pertenecientes a poblaciones reales (Vinuesa et al., 1997: 78).

Las primeras Tablas tipo describían en forma matemática las variaciones de la mortalidad por edad, pero tuvieron problemas al obtener las gráficas en forma de U o J de las tasas de mortalidad por grupos de edades. Posteriormente relacionaron el riesgo de morir para una determinada edad, con los riesgos de morir observados en otros grupos de edades o con riesgos de morir revisados en otras poblaciones en edades similares. Las Tablas modelos se obtienen de un análisis de riesgos de morir para poblaciones reales y las Tablas de vida modelo de las Naciones Unidas. Se eligen de aquellas que sean recomendables de acuerdo con condiciones de vida similares para determinadas regiones (CELADE, 1975, 2004, 2007a, 2007b, 2010).

 

Tablas de vida modelo de las Naciones Unidas

En 1955, la División de Población de la Secretaría de las Naciones Unidas desarrolló el primer conjunto de Tablas modelo (Naciones Unidas, 1983), basado en 158 Tablas de vida observadas por sexo; la información era poco confiable pues se emplearon muchas Tablas de países en desarrollo. La información de la población para grandes zonas del mundo no estaba almacenada en base de datos, ya que esos países carecían de estadísticas de mortalidad, por lo que los datos fueron muy criticados por resultar deficientes. Sin embargo, esta información sentó las bases para los trabajos posteriores sobre las cuales se desarrolló un sistema de Tablas modelo de vida.

Los patrones de mortalidad por edades se modificaron respecto a la información recabada durante 1850-1960. Por esta razón, la División de Población del Departamento de Asuntos Económicos y Sociales Internacionales de la Secretaría de las Naciones Unidas publicó un conjunto de Tablas de vida modelo basadas en datos de países en desarrollo (Naciones Unidas, 1983). Se construyó una nueva base de datos formada por 36 Tablas de mortalidad por sexo (72 en total); geográficamente, 16 pares de Tablas de mortalidad masculinas-femeninas se obtuvieron de diez países de Latinoamérica, 19 de 11 países de Asia y una de África.

En estas Tablas de vida modelo de las Naciones Unidas se identificaron diversos patrones de probabilidades de morir por edades. Se identificaron, en términos regionales, cuatro patrones distintos de mortalidad: los patrones "latinoamericano", "chileno", "sudasiático" y "extremoriental". Se construyó un quinto patrón como promedio general de los anteriores, llamado "general".

En el modelo latinoamericano, la tendencia de la mortalidad es elevada en los primeros años de vida, debido a enfermedades diarreicas y parasíticas; situación similar en los primeros años de la edad adulta, por causa de accidentes; mientras que en las edades mayores tiende a ser bajo el nivel de mortalidad (CEPAL/UNFPA, 2005; CELADE, 2004). El patrón "chileno" se caracteriza principalmente por una mortalidad infantil extremadamente elevada (debido a enfermedades respiratorias y un destete temprano), en comparación con la observada en la niñez.

La tendencia de mortalidad en el patrón "sudasiático" es sumamente alta, por debajo de los 15 años y también en las edades avanzadas (arriba de los 55 años), por lo que en las primeras edades adultas es relativamente baja. Las causas de muerte dadas a conocer por el Centro Internacional de Investigaciones sobre Enfermedades Diarreicas en Bangladesh y por el Proyecto Modelo de Registro en la India, revelan que se deben a enfermedades diarreicas y parasíticas en las edades más jóvenes y a enfermedades diarreicas y respiratorias en las edades avanzadas.

El patrón extremo oriental presenta tasas muy elevadas de mortalidad en las edades avanzadas en comparación con las de las edades más jóvenes, esto debido a la incidencia de tuberculosis en el pasado.

 

Funciones de la tabla de mortalidad

Las diversas funciones que contiene una tabla de mortalidad, su significado y la fórmula de cálculo de cada una de ellas son importantes porque las funciones de la tabla son de uso frecuente en diversos problemas demográficos.

Las funciones de la tabla de vida son las siguientes:

_nm_x Tasa específica de mortalidad por edad

_nq_x Probabilidad de muerte

l_x Supervivientes a edad exacta

_nL_x Población estacionaria de la tabla

_nZ_x Probabilidad perspectiva de paso

donde:

x Edad exacta a inicio del intervalo de edad

n Amplitud del intervalo de edad

Tasa específica de mortalidad por edad (_nm_x)

Se calculan a partir del número de defunciones ocurridas en la población en un determinado grupo de edad, comprendido entre las edades exactas x y x+n, y de los años-persona vividos por la población en ese grupo de edad. Cuando la medida equivalente se calcula para una población estacionaria se utiliza _nM_x.

Probabilidad de muerte (q_x)

Representa la probabilidad que tiene una persona de edad exacta x de fallecer dentro del año que sigue al momento en que alcanza dicha edad:

Los cocientes tienen como denominador a la población sometida a riesgo al principio del intervalo de duración o edad considerados. Por lo regular no se calculan directamente a partir de los datos brutos de defunciones y población, sino tomando como base las tasas de mortalidad por edad. En este trabajo se tomó el método actuarial, que consiste en un reparto lineal de los acontecimientos dentro del intervalo de edad:

Al tratarse de una probabilidad el valor no puede ser superior a uno, aunque dicho valor puede darse en tanto por mil o en porcentaje.

Supervivientes (1_x)

Representa el número de personas que alcanzan con vida la edad exacta x de una generación inicial de (1₀) nacimientos. Se dice que esta función muestra "la extinción de una generación por muerte". El valor inicial (1₀) se conoce como la raíz de la tabla y por lo regular se fija como raíz de la tabla una constante arbitraria, tal como cien mil o la unidad. Una vez fijada la raíz, esta función depende solamente de la edad x, a diferencia de la mayoría de las defunciones de la tabla, que depende tanto de la edad x como de la amplitud del intervalo n.

Se designa con ω la edad en la cual el número de sobrevivientes se hace igual a cero. Usualmente ω toma valores cercanos a los cien años, pero este punto no tiene mayor importancia para propósitos demográficos, donde generalmente se trabaja con la población de las últimas edades agrupadas, por lo cual las Tablas se elaboran hasta una edad suficientemente avanzada, por ejemplo 85 o 90 años, incluyéndose en ocasiones un grupo abierto final. La fórmula que se aplica es:

1_{x + n} = 1_x - (1_x * _nq_x) (3)

Población estacionaria (_nL_x)

La población estacionaria asociada a la tabla representa el total de tiempo vivido dentro de un intervalo de edad de una población con las características de mortalidad que refleja la tabla. Se estima por la ecuación 4:

_nL_x = n * [0.5 * (l_x + l_{x + n})] (4)

Probabilidad perspectiva de paso (_nz_x)

Se calcula por medio de la ecuación (5), entre intervalos de edad, tomando la población estacionaria de la tabla.

Es imprescindible que la amplitud del intervalo de edad (n) sea el mismo tanto en el numerador como en el denominador, por lo que cuando se construye una Tabla de mortalidad por grupos quinquenales de edad se definen variantes de la fórmula general. Para calcular la probabilidad perspectiva desde el nacimiento hasta el primer grupo quinquenal de edad (0 a 4), se calcula por la ecuación:

donde el denominador es el quíntuplo de la raíz de la tabla.

La siguiente probabilidad se estima utilizando la ecuación:

Para el resto de las edades se ocupa la fórmula general.

 

Modelo matemático

El modelo de Ricard Genova se emplea para obtener las proyecciones de las Tablas de mortalidad hasta el año horizonte 2030 para el estado de Puebla. El método se aplica en primera instancia para las mujeres y posteriormente se harán los cálculos similares para los hombres.

 

El modelo de Ricard Genova

El modelo creado por Genova (1994) se basa en lo siguiente:

1. El elemento que se proyecta es la esperanza de vida de las mujeres al nacer hasta un máximo alcanzable en un futuro teórico muy alejado del año horizonte (2030), que es el último año proyectado.

2. Se obtienen los valores intermedios de las esperanzas de vida, entre el proporcionado por la última tabla conocida y el máximo teórico, de acuerdo con la evolución registrada en el pasado.

3. Se seleccionan dos Tablas tipo para ajustar la esperanza de vida del año horizonte y así obtener un coeficiente con el que se van a calcular las tasas específicas de mortalidad por grupos de edad.

4. Se calculan las tasas específicas de mortalidad de las Tablas de los años intermedios interpolando linealmente entre las tasas de la última tabla conocida y la estimada en el año horizonte.

 

Aplicación del modelo Ricard Genova para obtener la Tabla de esperanza de vida en mujeres para el estado de Puebla

Se fija una esperanza de vida de 82 años (CONAPO, 2008) alcanzable en el año 2100 alejado del año horizonte 2030 (CONAPO, 2005, 2008).

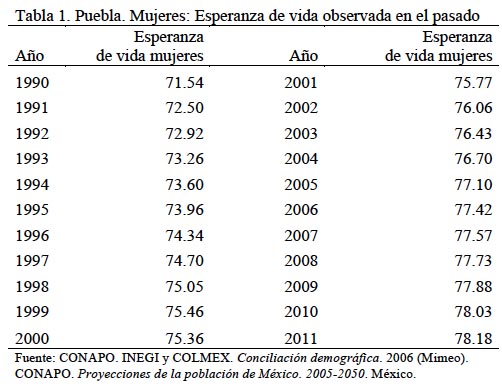
A continuación se calculan las esperanzas de vida de los años intermedios. Estas esperanzas estarán entre la esperanza de vida del año 2010, que es la esperanza de vida de partida y la máxima del año 2100. Estas esperanzas de vida intermedias se calculan tomando en cuenta las esperanzas de vida de años anteriores, en este caso se consideraron las esperanzas de vida e^t₀ de los años 1990 a 2011 (ver Tabla 1).

Las esperanzas de vida se transforman en logits (Bulatao et al., 1989), lo cual se expresa por la:

donde para e₀^max 82 aquí se fijó e₀^min = 37 (INEGI, 2001, 2009). Los valores transformados aparecen en el Tabla 3.

A continuación se construye un modelo de regresión lineal para los logits que aparecen como variables endógenas (y) y los años como variables exógenas (x) (Montgomery, 2002; Levin, 2004; Gujarati, 2010). Los resultados de la estimación se obtienen usando el software SPSS para Windows y se presentan en el Tabla 2.

La recta de regresión estimada (9) queda:

Teniendo en consideración (8), se calculan los logit estimados para los años 1990 a 2030 (ver columna D de la Tabla 3). Los logit estimados para cada uno de los años se transforman en esperanzas de vida mediante la siguiente expresión (10 que a su vez es obtenida de la ecuación (8) (columna E de la Tabla 3):

La evolución de la serie de esperanzas de vida observada y estimada (columnas B y E, respectivamente, de la Tabla 3) para el periodo 1990-2010, queda reflejada en la Gráfica 1.

En la serie estimada final se utilizan las esperanzas observadas para los años 1990 a 2010. En el año 1990 la observada es -0.06328 años menor que la estimada (78.0308 frente a 78.0941). La diferencia entre ambos se distribuye progresivamente en un periodo de 20 años, desapareciendo en el año 2030 (ver columna F de la Tabla 3):

en 2010: e^t₀ = 78.0941 + (-0.06328*1.00) = 78.0308

en 2015: e^t₀ = 78.9753 + (-0.06328*0.75) = 78.9278

en 2020: e^t₀ = 79.6689 + (-0.06328*0.50) = 79.6373

en 2025: e^t₀ = 80.2103 + (-0.06328*0.25) = 80.1945

en 2030: e^t₀ = 80.6300 + (-0.06328*0.00) = 80.63

Se calculan las esperanzas de vida para cada uno de los años intermedios de la serie utilizando interpolación lineal en las esperanzas de vida ajustadas en los años calculados. Por ejemplo, para el periodo 2011-2013 el cálculo sería el siguiente:

en 2011: e^t₀ = 78.0308 + ((78.9278 - 78.0308) * 0.2) = 78.2102

en 2012: e^t₀ = 78.0308 + ((78.9278 - 78.0308) * 0.4) = 78.389

en 2013: e^t₀ = 78.0308 + ((78.9278 - 78.0308) * 0.6) = 78.5690

Los resultados se reflejan en la Tabla 4, en donde se proyectan para los años 2011-2030).

A partir de la serie de esperanzas de vida se calculan las tasas de mortalidad por edad para el año 2030. Esto se lleva a cabo mediante interpolación lineal de las tasas específicas de mortalidad de dos Tablas tipo que encierren la esperanza de vida del año horizonte (Naciones Unidas, 1983, 1986). En este caso, dicha esperanza de vida es 80.63 y se sitúa entre los 80 años de la Tabla tipo nivel 25 y los 82.5 años de la Tabla tipo nivel 26, ambas de la ONU región oeste, con incrementos de 2.5 (ver Tabla 5). El coeficiente de interpolación lineal se obtiene despejando c de la expresión:

(1 - c)x + cy = z donde 0 ≤ c ≤ 1 (11)

Para el caso del estado de Puebla se tiene:

C²⁰³⁰ = (80.63 - 80) / 82.5 - 80)

C²⁰³⁰ = 0.25

El cálculo de la tasa de mortalidad en el grupo de x a x + 4 años será:

M²⁰³⁰ (x) = M_{niv_2} (x) * C²⁰³⁰ + [(1 - C²⁰³⁰) * M_{niv_1}(x)]

Por ejemplo, para x = 10 la tasa correspondiente será:

M²⁰³⁰ (10) = 0.00011782 * 0.25 + (1 - 0.25) * 0.00015510

M²⁰³⁰ (10) = 0.0001

Las tasas calculadas para el año 2030 se muestran en el Tabla 5. También se añaden las tasas de mortalidad del año de partida, 2010 (INEGI, 2011).

Se calculan las tasas de mortalidad específicas para el resto de los años de la proyección, desde el año 2011 hasta 2029. Se aplica, para cada año, interpolación lineal entre las tasas de la última tabla conocida —la de 2010— y la estimada para el año horizonte, 2030.

Como se observa en la Tabla 5, todos los grupos de edad presentan mayor tasa de mortalidad en 2010 que en el 2030, es decir que en todos los grupos de edad disminuye la mortalidad en el periodo 2010-2030.

Retomando el cálculo de las tasas específicas de mortalidad, el coeficiente se obtiene a partir de las esperanzas de vida de las Tablas de 2010 y de 2030.

Por ejemplo, para el año 2015:

C²⁰¹⁵ = (78.9278 - 78.0308) / (80.63 - 78.0308)

C²⁰¹⁵ = 0.35

Para ese año las tasas para el tramo de edad [x; x + 4] se obtendrán como sigue:

M²⁰¹⁵ (x) = M²⁰³⁰ (x) * C²⁰¹⁵ + [(1 - C²⁰¹⁵) * M²⁰¹⁰(x)]

Por ejemplo para x = 10:

M²⁰¹⁵ (10) = 0.0001 * 0.35 + [(1 - 0.35) * 0.0003]

M²⁰¹⁵ (10) = 0.0002

El proceso se repetiría para todos los grupos de edad y para todos los años.

 

Elaboración de la Tabla de mortalidad abreviada por sexo y edad

La última fase de la proyección es completar el resto de los elementos que componen la tabla de mortalidad. Las funciones que componen las Tablas abreviadas de vida son las siguientes: _nm_x, _nq_x, l_x, _nL_x, _nZ_x, Como se explicó anteriormente, las Tablas de mortalidad abreviada de mujeres proyectadas se calcularon para los años de 2011 hasta 2030. Se presenta la del año 2030 (Tabla 6).

 

Resultados para los hombres aplicando el método Ricard Genova

Procediendo de forma similar al caso anterior, se consideran las esperanzas de vida (Tabla 7).

Se transforman en logits a partir de la función logit (16) recomendada por el Banco Mundial:

donde para e₀^max = 77 se fijó e₀^min = 36 (INEGI, 2001, 2009). Los valores transformados aparecen en la Tabla 9.

A continuación se construye un modelo de regresión lineal para los logits que aparecen como variables endógenas (y) y los años como variables exógenas (x) (Montgomery, 2002; Levin, 2004; Gujarati, 2010). Los resultados de la estimación se obtienen usando el software SPSS para Windows y se presentan en la Tabla 8.

La recta de regresión estimada queda:

La aplicación de la ecuación (10) a la observada para cada año (columna B de la Tabla 9) permite obtener el logit observado (columna C de la Tabla 9). Posteriormente se aplica la ecuación (16) para obtener el logit estimado (columna D de la Tabla 9), que se transforma en esperanza de vida aplicando la ecuación (10) (columna E de Tabla 9). En la Gráfica 2 se muestra la evolución de la esperanza de vida al nacer para el periodo 1990-2010, teniendo en consideración la ecuación (17).

Finalmente se ajusta durante un periodo de 20 años la diferencia entre la esperanza observada en el año 2010 (73.0187) y la estimada (73.03655); en este caso el resultado es -0.01785. La serie estimada final de esperanzas de vida masculina al nacer se presenta en la columna F de la Tabla 9.

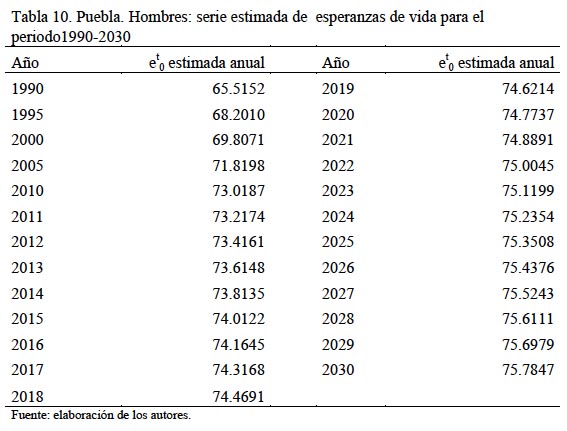
Las esperanzas de vida para cada año se obtendrán aplicando interpolación lineal entre las esperanzas de vida ajustadas cada cinco años, como se presenta en la Tabla 10.

El coeficiente C²⁰³⁰ para hombres es el siguiente:

C²⁰³⁰ = (75.78 - 75) / (77.5 - 75)

C²⁰³⁰ = 0.31

donde: e₀²⁰³⁰ = 75.78 y 75 y 77.5 son las esperanzas de vida al nacer de las tabla tipo nivel 23 y 24, respectivamente, de la ONU, Región Oeste con incrementos de 2.5.

En la Tabla 11 se presentan las tasas de mortalidad del año 2030, construidas a partir de dicho coeficiente. También se incorporan las tasas de mortalidad del año 2010.

Las tasas específicas de mortalidad por grupos de edades para cada año se obtienen interpolando entre las tasas del año de partida, 2010 y las del año horizonte, 2030.

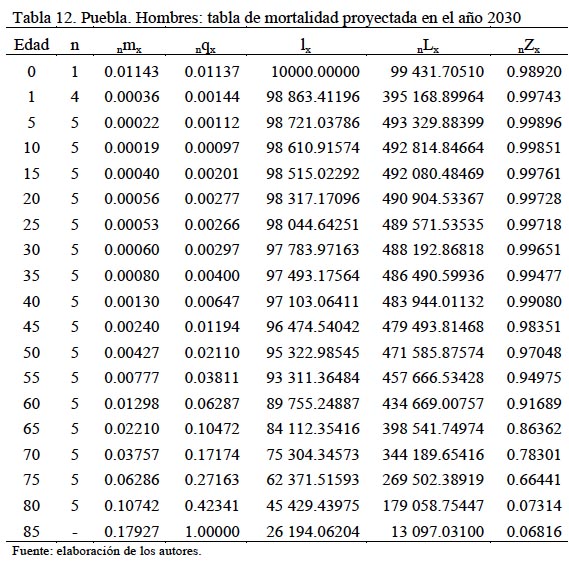
Las Tablas de mortalidad abreviada de hombres proyectadas se calculan para los años de 2011 hasta el año 2030. Aquí sólo se presenta la del año 2030 (Tabla 12).

 

Comportamiento de las Tablas de mortalidad para hombres y mujeres

Las Gráficas 3 y 4 presentan las tasas de mortalidad femenina y masculina, respectivamente, proyectadas en función del tiempo para las distintas edades consideradas.

Partiendo de la certeza que los individuos tendrán que fallecer, queda como incertidumbre el momento de la ocurrencia de este hecho, es decir, la edad a la que ocurrirá el deceso; no obstante, a partir del cálculo de la Tabla de mortalidad basada en las tasas observadas, en ambos casos se logra obtener las tasas de mortalidad por edad y sexo.

En las curvas de evolución de la tasa de mortalidad se visualiza que la tasa máxima de mortalidad varía con la edad. A mayor edad, mayor tasa de mortalidad, situación que se observa independientemente del sexo de los individuos. Esta condición se deriva de las causas naturales del envejecimiento; no obstante, al introducir el riesgo que se tiene de fallecer antes de la edad máxima esperada, se pueden apreciar diferencias notables al revisar los valores de las tasas de acuerdo con el sexo.

Retomando el caso de las mujeres, en la Gráfica 3 se muestra la tasa de mortalidad femenina. El cálculo parte de una esperanza de vida con un límite máximo de 82 años y un mínimo de 37 años. Como se puede observar, todos los grupos de edad presentan para 2011 las mayores tasas de mortalidad proyectadas y se espera disminuyan paulatinamente durante el periodo 2011-2030. En los primeros grupos de edad se observa el mayor número de decesos, caso contrario a los de mayor edad que registran disminución. El esperado retroceso de la mortalidad puede ser resultado del uso de la medicina preventiva y los programas de salud.

Realizando comparaciones entre sexos utilizando las gráficas de mortalidad, se observan mayores tasas de mortalidad para los hombres que para las mujeres. En el caso de los hombres, (Gráfica 4) si bien en los grupos de edad de 0 a 69 años se obtiene una disminución de la mortalidad, se prevé que habrá un ligero aumento en la mortalidad para los grupos de edad a partir de los 70 años.

Es importante mencionar que para el cálculo de estas tasas los límites mínimos y máximos de la esperanza de vida que se tomaron fueron 36 y 77 años, respectivamente. Las diferencias en los límites reflejan el fenómeno de la menor esperanza de vida de los hombres, quienes en general viven alrededor de cinco años menos que las mujeres.

La mayor probabilidad de muerte de los hombres a edad avanzada respecto al comportamiento de las mujeres se observa en el trazo de la Gráfica 4 (0.144 contra 0.137) para el grupo de 85 años o más y su comportamiento es ascendente hasta alcanzar 0.179. Este indicador muestra la probabilidad de que un grupo de personas de la misma generación fallezca antes de cumplir el siguiente año.

Como es de suponer, a menor edad, menor posibilidad de muerte. Sin embargo, se observa que al arranque de la vida las mujeres registran una menor probabilidad de muerte; para 2011, ésta es de 0.018 y de 0.022 para los hombres. En las proyecciones para 2030 se espera que esa probabilidad se reduzca respecto a 2011 tanto para hombres como para mujeres, al igual que la brecha que separa a ambos géneros (gráficas 5 y 6).

La menor probabilidad de muerte en mujeres la registra el grupo de cinco a nueve años. Este grupo de edades presenta los menores valores de la tabla; por otro lado. a partir de los 65 años o más el comportamiento se estabiliza y es casi lineal (ver Gráfica 5).

Es de resaltar el comportamiento de la Gráfica 6 en el grupo de edades de 1 a 4 años, quienes registran la menor probabilidad de muerte de toda la serie.

El análisis de la supervivencia parte de la premisa de que lo inevitable para cierto grupo de edad (85 o más) es la muerte y expresa la reducción progresiva de un grupo de individuos a causa de los fallecimientos, por lo que se constituye en una relación superviviencia/mortalidad.

Las curvas de superviviencia se muestran en las gráficas 7 y 8. En éstas se observa cuantos efectivos del cohorte alcanzan cada año las diferentes edades. Es decir, de cada cien mil habitantes que apenas están por cumplir un año, por ejemplo en 2011, en el caso de las mujeres sólo 37 907 tienen una expectativa de cumplir 85 o más años, mientras que en el caso de los hombres dicha expectativa sería de 27 842 (ver Gráfica 7 y Gráfica 8).

Con el transcurso de los años la probabilidad de superviviencia va disminuyendo a causa del proceso degenerativo natural y de la exposición a enfermedades mortales (INEGI, 2013) o bien a fenómenos exógenos como los accidentes de transporte, los cuales son causa significativa de defunciones.¹

En los cálculos de superviviencia se considera una población estacionaria, en donde el crecimiento natural de la población (nacimientos y defunciones) permanece constante a lo largo del tiempo, descartando con ello fenómenos abruptos como podrían ser las epidemias.

De acuerdo con los datos obtenidos para 2030, la probabilidad de superviviencia será mayor que para 2011, lo cual impacta positivamente a la esperanza de vida de la población femenina. No obstante, estudios biométricos concluyen que la brecha que existe entre sexos se reducirá debido a que la mujer al insertarse cada vez más en el mercado laboral quedará más expuesta a mayores riesgos.²

 

Conclusiones

Al analizar los resultados obtenidos durante el periodo 2011-2030, se observa una tendencia en la reducción de la mortalidad en el Estado de Puebla, que en este trabajo es lo que se esperaba obtener. Existen factores que indudablemente afectan estos índices o pueden modificarlos. Estos factores están correlacionados con las políticas de población que dicen mucho del bienestar y de la salud de la población y que corresponden a diferentes programas de prevención, como la extensión en la atención primaria con programas de vacunación masiva, terapias de rehidratación oral, lactancia materna y control de la salud de las personas sanas de todas las edades (en particular la de los niños). Los adelantos de la ciencia médica y mejores niveles nutricionales y educativos de la población influirán definitivamente en la reducción de los volúmenes de la mortalidad. Los estudios demográficos en países desarrollados consideran las Tablas de mortalidad un instrumento para medir la eficacia de sus políticas de población, ya que la esperanza de vida tiene relación directa con la salud de la población.

En México y en particular en el estado de Puebla, los estudios demográficos relacionados con la mortalidad son incipientes y las Tablas de mortalidad oficiales publicadas en el Diario Oficial de la Federación pueden ser las mismas hasta por más de una década. Las medidas basadas en registros administrativos y los censos de población en las Tablas de mortalidad también presentan las mismas limitaciones. Los datos sobre las edades y los registros administrativos de las estadísticas vitales pueden ser incompletos o sesgados, afectando de manera sensible los resultados de las tablas. Por lo anterior es posible afirmar que la falta de la proyección de estos estudios implica una grave falla de planeación de las condiciones de bienestar de la población. El método de Ricard Genova utilizado en este trabajo permite el uso de Tablas de vida modelo que han sido trabajadas de acuerdo con los patrones de mortalidad de una población. Comparados con los patrones de mortalidad de nuestro país coinciden y permiten hacer una proyección, hasta el año horizonte de 2030.

Analizando los resultados de las Tablas de mortalidad de Puebla, se concluye que la esperanza de vida al nacer muestra que las mujeres son más longevas que los hombres, pues la esperanza de vida es 4.93 años mayor en promedio en ellas. Las excepciones a esta regla podrían darse en países con alta fecundidad y alta mortalidad materna o en poblaciones donde por razones culturales la nutrición y las condiciones de vida de la mujer son marcadamente peores que las del hombre.

Para la población de edades 0-4 es preferible separar el cálculo para la edad 0 y ocasionalmente para la edad un año del grupo de edades 1-4 o 2-4, debido a que hay divergencias en la mortalidad de este intervalo. Es preferible calcular directamente las probabilidades de muerte al primer y segundo año utilizando las estadísticas de nacimientos y defunciones infantiles.

Las Tablas de mortalidad también presentan las limitaciones de cualquier medida basadas en registros administrativos y censos de población. Los datos sobre las edades y los registros administrativos de las estadísticas vitales pueden ser incompletos o sesgados, afectando de manera sensible los resultados de las tablas. El modelo aplicado en este trabajo resalta la utilización de las tablas modelo propuestas por la ONU, teniendo en consideración las condiciones de bienestar y salud de la población, lo que hace más suaves los sesgos relacionados con las imprecisiones de los datos.

 

Bibliografía

ALBA, H. F., 1974, La población de México, Series CICRED, Centro de Estudios Económicos y Demográficos, El Colegio de México, México.         [ Links ]

BULATAO, R. A. et al., 1989, "Projecting mortality for all countries", en Working paper, núm. 337, World Bank, Washington.         [ Links ]

CELADE, 1975, La demografía como ciencia, serie Población y desarrollo, núm. 58, publicación de las Naciones Unidas, Centro Latinoamericano de Demografía, recuperado de http://www.facso.uchile.cl/observa/dinamica%20demografica.pdf, Santiago de Chile.         [ Links ]

CELADE, 2004, América Latina: Tablas de mortalidad, 1950-2025, Publicación de las Naciones Unidas, Centro Latinoamericano de Demografía, recuperado de http://www.eclac.org/publicaciones/xml/3/19673/bol-dem74.pdf, Santiago de Chile.         [ Links ]

CELADE, 2007a, Mortalidad, Publicación de las Naciones Unidas, Centro Latinoamericano de Demografía, recuperado de http://www.eclac.org/publicaciones/xml/5/33265/2007-1080-OD4.pdf, Santiago de Chile.         [ Links ]

CELADE, 2007b, Proyección de población, Publicación de las Naciones Unidas, Centro Latinoamericano de Demografía, recuperado de http://www.eclac.cl/publicaciones/xml/4/32634/2007-724-OD3-web.pdf, Santiago de Chile.         [ Links ]

CELADE, 2010, Mortalidad, Publicación de las Naciones Unidas, Centro Latinoamericano de Demografía/División de Población de la CEPAL, recuperado de http://www.cepal.org/publicaciones/xml/5/43575/OD9-LCG1111.pdf, Santiago de Chile.         [ Links ]

CEPAL/UNFPA, 2005, Dinámica demográfica y desarrollo en América Latina y el Caribe, serie Población y desarrollo, núm. 58, Publicación de la Comisión Económica para América Latina y el Caribe/Fondo de Población de las Naciones Unidas, Naciones Unidas, Santiago de Chile.         [ Links ]

CONAPO, 2005, Principales causas de muerte en las etapas del curso de vida, 1980-2002, Consejo Nacional de Población, Serie Documentos Técnicos, México.         [ Links ]

CONAPO, 2008, Proyecciones de la población de México, de las entidades federativas, de los municipios y de las localidades, 2005-2050, Documento metodológico, Consejo Nacional de Población, México.         [ Links ]

DE VICENTE, A., J. HERNÁNDEZ, I.ALBARRÁN y C. RAMÍREZ, s/f, Proyección y estudio de una población: el papel de la mortalidad.         [ Links ]

GENOVA, R., 1994, La mortalidad en la proyección multiregional de la población española, Instituto de Demografía (CSIC), Madrid.         [ Links ]

GUJARATI, D. y D. PORTES, 2010, Econometría, McGraw-Hill/Interamericana Editores. México.         [ Links ]

INEGI, 1990, Anuario estadístico del estado de Puebla 1990, Instituto Nacional de Estadística y Geografía, Gobierno del Estado de Puebla, México.         [ Links ]

INEGI, 2001, Indicadores sociodemográficos de México, 1930-2000, Instituto Nacional de Estadística y Geografía, recuperado de http://www.inegi.org.mx/prod_serv/contenidos/espanol/bvinegi/productos/integracion/sociodemografico/indisociodem/2001/indi2001.pdf, México.         [ Links ]

INEGI, 2009, Estadísticas históricas de México 2009, Instituto Nacional de Estadística y Geografía, recuperado de http://www.inegi.org.mx/prod_serv/contenidos/espanol/bvinegi/productos/integracion/pais/historicas10/EHM2009.pdf, México.         [ Links ]

INEGI, 2011, Anuario estadístico de Puebla 2011, Instituto Nacional de Estadística y Geografía, Gobierno del Estado de Puebla, México.         [ Links ]

INEGI, 2011, Principales resultados del Censo de Población y Vivienda 2010: Hidalgo, INEGI, recuperado de http://www.inegi.org.mx/prod_serv/contenidos/espanol/bvinegi/productos/censos/poblacion/2010/princi_result/hdo/13_principales_resultados_cpv2010.pdf, México.         [ Links ]

INEGI, 2013, Estadisticas de Mortalidad, recuperado de http://www.inegi.org.mx/est/contenidos/proyectos/registros/vitales/mortalidad/tabulados/ConsultaMortalidad.asp        [ Links ]

LEVIN, R.I. y D. S. RUBIN, 2004, Estadística para administración y economía, Pearson Educación, México.         [ Links ]

LIVI-BACCI, M., 1993, Introducción a la demografía, Editorial Ariel, Italia.         [ Links ]

MALDONADO, P., 2005, Demografía: conceptos y técnicas fundamentales, Plaza y Valdés, México.         [ Links ]

MINA-VALDÉS, A., 2006, "Ley de mortalidad mexicana, funciones de supervivencia", en Estudios Demográficos y Urbanos en línea, mayo-agosto, año/vol. 21, núm. 2, recuperado de http://www.redalyc.org/src/inicio/ArtPdfRed.jsp?iCve=11221117003        [ Links ]

MINA-VALDÉS, A., 2011, La obtención y proyección de tablas de mortalidad empleando curvas Spline, en Papeles de Población, en línea, vol. 17, recuperado de http://www.redalyc.org/src/inicio/ArtPdfRed.jsp?iCve=11221117003        [ Links ]

MONTGOMERY, D. E. PECK y G. VINING, 2002, Introducción al análisis de regresión lineal, Grupo Patria Cultura, México.         [ Links ]

NACIONES UNIDAS, 1983, Tablas modelo de mortalidad para países en desarrollo, Publicación de las Naciones Unidas, recuperado de http://www.un.org/esa/population/publications/Model_Life_Tables/Model_LT_Preface_TOContents_SP.pdf        [ Links ]

NACIONES UNIDAS, 1986, Manual X: técnicas indirectas de estimación demográfica, Publicación de las Naciones Unidas, recuperado de http://unstats.un.org/unsd/demographic/standmeth/handbooks/Manual_X-es.pdf        [ Links ]

ONE/CEPD, 2004, La Esperanza o Expectativa de Vida 2001-2003. Cálculos y Análisis por sexo y edades, Oficina Nacional de Estadísticas/Centro De Estudios de Población y Desarrollo Cuba/Fondo de Población de las Naciones Unidas, recuperado de http://www.google.com.mx/url?sa=t&rct=j&q=&esrc=s&source=web&cd=3&ved=0CDIQFjAC&url=http%3A%2F%2Fwww.ccsr.ac.uk%2Fcuba%2FCEPDE2004%2FESPERANZA%2FCuba.%2520Esperanza%2520de%2520vida%252020012003.pdf&ei=xCBxU7a#mIePk8gGHi4Bo&usg=AFQjCNGq3ZWozH53LiguDocrxXNWJTVFlQ#, La Habana.         [ Links ]

ORTÍZ, L. Assael, 1999, Información sociodemográfica, proyecciones de población y proyecciones derivadas para la región Hidalgo, Puebla y Tlaxcala, 1990-2030, Universidad Autónoma del Estado de Hidalgo, México.         [ Links ]

RAMÍREZ, F. G., 2000, Análisis de la situación de salud: análisis de la mortalidad y medición de la mortalidad, recuperado de http://www.academia.edu/5349577/DOCUMENTOS_METODOLOGICOS_Serie_Analisis_de_la_Situacion_de_Salud, Lima, Perú         [ Links ].

VINUESA, J., F. ZAMORA, R. GENOVA, P. SERRANO y J. RECAÑO, 1997, Demografía: análisis y proyecciones, Editorial Síntesis, España.         [ Links ]

 

Notas

1 http://conapra.salud.gob.mx/

2 http://www.stps.gob.mx/bp/secciones/dgsst/estadisticas/Nacional%202001-2010.pdf

 

Información sobre los autores

Gerardo Martínez Guzmán. Obtuvo el título de Licenciado en Matemáticas. Maestría y Doctorado en Ciencias Matemáticas por la Facultad de Ciencias Físico Matemáticas de la Benemérita Universidad Autónoma de Puebla, México. Actualmente es profesor investigador de la Facultad de Ciencias de la Computación de la Benemérita Universidad Autónoma de Puebla, México. Dirección electrónica: gguzman@cs.buap.mx

Mario Mauricio Bustillo Díaz. Obtuvo el título de ingeniero en el Instituto Politécnico de Odesa (Ucrania-CCCP) en Ciencias de la Computación y la Maestría en Ciencias en el área de Arquitecturas de Computadoras. Recibió el título de Ph.Dr. en la Universidad Politécnica Estatal de San Petersburgo (Rusia), en la especialidad de sistemas difusos. Actualmente se desempeña como Profesor-Investigador en la Benemérita Universidad Autónoma de Puebla, México. Dirección electrónica: bustillo@cs.buap.mx

Rogelio González Velázquez. Obtuvo el título de Licenciado en Matemáticas por la Facultad de Ciencias Físico Matemáticas de la Universidad Autónoma de Nuevo León, la Maestría en Investigación de Operaciones en la División de Estudios de Posgrado de la Facultad de Ingeniería de la Universidad Nacional Autónoma de México y recibió el grado de Doctor en Logística y Dirección de la Cadena de Suministro en el Departamento de Ingeniería de la Universidad Popular Autónoma del Estado de Puebla. Actualmente se desempeña como profesor investigador adscrito a la Facultad de Ciencias de la Computación de la Benemérita Universidad Autónoma de Puebla, México. Dirección electrónica: rgonzalez@cs.buap.mx

María Beatriz Bernabé Loranca. Nació en la ciudad de Puebla, México. Recibió el grado de Licenciada en Ciencias Computacionales por la Benemérita Universidad Autónoma de Puebla (BUAP), México in 1993 y el grado de Maestría en Ingeniería en Calidad por la Universidad Iberoamericana (UIA), México in 2003. En enero de 2010, recibió el grado de Doctora en Ingeniería en Investigación de Operaciones por Universidad Nacional Autónoma de México (UNAM). Desde 1995 ha sido profesora de la Facultad de Ciencias de la Computación BUAP, trabajando en estadística, teoría de la computación y bases de datos. Desde 2010 pertenece al Sistema Nacional de Investigadores en nivel candidato. Sus áreas de interés son optimización combinatoria, diseño territorial y técnicas multiobjetivo. Dirección electrónica: beatriz.bernabe@gmail.com

Alejandro Rangel Huerta. Es Doctor en ciencias Físico Matemáticas egresado de la Universidad Autónoma Metropolitana Unidad Iztapalapa México. Ha trabajado en las líneas de investigación de modelado y simulación de sistemas. Actualmente colabora en las áreas de Inteligencia Artificial de sistemas colectivos y temas relacionados. Es profesor investigador en la Facultad de Ciencias de la Computación de la Benemérita Universidad Autónoma de Puebla, México. Dirección electrónica: arangel@cs.buap.mx

Gabriel Juárez Díaz. Obtuvo el título de ingeniero en electrónica en el Instituto Tecnológico de Puebla, la Maestría en Ciencias en el área de Dispositivos semiconductores en la Benemérita Universidad Autónoma de Puebla y recibió el título de Doctor en ciencias en el Centro de investigación y de estudios avanzados del IPN en la especialidad de electrónica de estado sólido. Actualmente se desempeña como Profesor investigador en la Benemérita Universidad Autónoma de Puebla, México. Dirección electrónica: j.gabriel@rocketmail.com 

Apolonio Ata Pérez. Licenciado en Electrónica por parte de la Universidad Autónoma de Puebla, y Maestro en Ingeniería en la especialidad de Automatización y Robótica por parte del Instituto Tecnológico de Puebla. Actualmente se desempeña como profesor investigador en la Benemérita Universidad Autónoma de Puebla. Dirección electrónica: Apolonio@cs.buap.mx

Nicolás Quiroz Hernández. Es Maestro en ciencias por el Instituto Nacional de Astrofísica, Óptica y Electrónica (INAOE). Licenciado en Electrónica por la Benemérita Universidad Autónoma de Puebla. Es profesor-Investigador de Medio tiempo en la Facultad de Ciencias de la Electrónica (FCE) de la BUAP, en donde se ha desempeñado como coordinador de los Laboratorios de Control, de Laboratorio Sistemas Digitales Básico y de Sistemas Digitales Avanzados, imparte clases en las licenciaturas de Electrónica y Mecatrónica en la Maestría en Ingeniería Electrónica con Opción en Instrumentación Electrónica. Colabora en la Facultad de Ciencias de la Computación de la BUAP, imparte clases en las licenciaturas de Ingeniería en Computación y en la Ingeniería de Tecnologías de la Información. Ha publicado más de 30 artículos en revistas y congresos nacionales e internacionales. Colabora con los cuerpos académicos de las unidades de la FCE y FCC de la BUAP. Es responsable de las materias de Programación y Programación Avanzada de la FCE. Dirección electrónica: niquiroz@gmail.com

Rosa María de Lourdes Reyes Vélez. Licenciada por la Facultad de Ciencias de la Computación, de la Benemérita Universidad Autónoma de Puebla. Actualmente labora en Instituto Nacional de Estadística y Geografía (INEGI) como analista de sistemas. Dirección electrónica: lulureve@hotmail.com