Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería, investigación y tecnología
versión On-line ISSN 2594-0732versión impresa ISSN 1405-7743
Ing. invest. y tecnol. vol.12 no.3 Ciudad de México jul./sep. 2011
Incorporación de un modelo de generador eólico al análisis de flujos dinámicos de potencia
Incorporation of a Wind Generator Model into a Dynamic Power Flow Analysis
Angeles–Camacho C.1 y Bañuelos–Ruedas F.2
1 Instituto de Ingeniería Universidad Nacional Autónoma de México. E–mail: CangelesC@iingen.unam.mx
2 Instituto de Ingeniería Universidad Nacional Autónoma de México. E–mail: Fbanuelosr@iingen.unam.mx
Información del artículo: recibido: agosto de 2009.
Reevaluado: abril de 2010.
Aceptado: julio de 2011.
Resumen
La energía eólica es hoy en día una de las opciones más efectivas y prácticas para la generación de electricidad a partir de energías renovables. Sin embargo, el incremento de la penetración de energía eólica provoca que los sistemas de potencia se vuelvan más dependientes y vulnerables a las variaciones de la velocidad del viento. El modelado es una herramienta que provee información valiosa de la interacción dinámica entre las turbinas eólicas y las redes de potencia a las que se conectan. El presente artículo desarrolla una caracterización realista de un modelo de la turbina eólica. El modelo de la turbina eólica se incorpora a un algoritmo para el análisis de su contribución a la estabilidad en una red eléctrica en el dominio del tiempo. La herramienta obtenida se conoce como flujos dinámicos de potencia. El modelo de la turbina toma en cuenta las velocidades del viento y la potencia reactiva consumida por el generador de inducción. El análisis de los flujos dinámicos de potencia que se presenta aquí, se realiza en función de los datos reales de la velocidad del viento recolectados en una estación de monitoreo del estado de Zacatecas en intervalos de 10 minutos. La generación inyectada en una parte de la red proporciona potencia localmente, reduciendo las pérdidas globales del sistema. Sin embargo, la variación de la potencia entregada por la central eólica causa fluctuaciones de la magnitud de voltaje y de los flujos de potencia en las líneas de transmisión.
Descriptores: generación eólica, flujos de potencia, penetración, estabilidad dinámica.
Abstract
Wind energy is nowadays one of the most cost–effective and practical options for electric generation from renewable resources. However, increased penetration of wind generation causes the power networks to be more depend on, and vulnerable to, the varying wind speed. Modeling is a tool which can provide valuable information about the interaction between wind farms and the power network to which they are connected. This paper develops a realistic characterization of a wind generator. The wind generator model is incorporated into an algorithm to investigate its contribution to the stability of the power network in the time domain. The tool obtained is termed dynamic power flow. The wind generator model takes on account the wind speed and the reactive power consumption by induction generators. Dynamic power flow analysis is carried–out using real wind data at 10–minute time intervals collected for one meteorological station. The generation injected at one point into the network provides active power locally and is found to reduce global power losses. However, the power supplied is time–varying and causes fluctuations in voltage magnitude and power flows in transmission lines.
Keywords: wind generation, power flows, penetration, dynamic stability.
Introducción
Las preocupaciones ambientales y políticas por un desarrollo sustentable han alentado el crecimiento de generación eléctrica a partir de energías renovables. La generación eólica es vista como una de las opciones más prácticas y con mejor costo–beneficio dentro de éstas. Sin embargo, dado que la velocidad del viento es variable en el tiempo, la electricidad generada variará. Sin una compensación reactiva apropiada, el voltaje en el punto de conexión a la red fluctuará de acuerdo con las variaciones de velocidad del viento. Este fenómeno puede afectar la estabilidad del sistema y comprometer la calidad de la energía de las cargas vecinas. Actualmente, la generación eólica integrada a sistemas eléctricos cubre una pequeña parte de la demanda total de potencia en donde la mayor generación se da por otras fuentes, como la hidráulica, la nuclear y combustibles fósiles. Si la penetración eólica o renovable en un sistema es pequeña, la generación síncrona convencional determinará el comportamiento dinámico del sistema (Slootweg et al., 2001). Los voltajes nodales son mantenidos dentro de sus límites de operación por esta generación centralizada. Sin embargo, con el incremento en la capacidad y el número de centrales eólicas adicionadas, éstas sustituirán la potencia proveniente de fuentes convencionales, de tal manera que su contribución no puede ser ignorada y no será posible el control de los voltajes nodales, usando los métodos tradicionales.
En los años recientes, la tendencia se ha movido de pequeñas centrales eólicas, a la planeación de centrales con algunos cientos de megawatts (MW) de capacidad, por ejemplo, el parque eólico "Eurus" en el estado de Oaxaca, México, el cual tiene una capacidad instalada de 250.5 MW. Este incremento de la penetración hace a las redes más dependientes y vulnerables a la variabilidad del recurso eólico. En el futuro serán conectadas grandes centrales eólicas directamente a los sistemas de transmisión. Los operadores de los sistemas de transmisión deberán implementar códigos de red que contengan altos estándares de calidad y estrictos requerimientos de conexión de centrales eólicas de gran tamaño. En general, la conexión es responsabilidad de los constructores de los parques eólicos (Ackerman, 2005).
El modelado de la interacción dinámica entre las centrales eólicas y los sistemas eléctricos proporciona información valiosa. Los inversionistas y las empresas pueden ejecutar los estudios necesarios preliminares a la conexión de las centrales. Una de las herramientas más utilizada en la planeación y el diseño de los sistemas eléctricos es el análisis de flujos de potencia, el cual calcula las condiciones de operación en estado estable del sistema. Una variante de esta herramienta es el análisis de flujos dinámicos, que permite el estudio en el dominio del tiempo con modelos de estado estable (Angeles, 2005). La potencia generada por la central eólica podrá ser prevista conociendo las mediciones del viento y el tipo de turbina a usar. El modelado de la red eléctrica permitirá analizar los efectos de la planta propuesta en función del tiempo.
La evaluación de los parámetros de la red en el tiempo, hará posible ver el rango completo de sus parámetros con cualquier inyección de potencia activa de la central eólica. La potencia activa inyectada por la central es difícil de predecir, dado que ésta varía proporcionalmente al cubo de la velocidad del viento y factores como la rugosidad son difíciles de establecer. Un modelo realista del viento y de la central eólica proporcionaría valores con una precisión media para determinar la inyección de potencia y los parámetros de las redes. Con el constante incremento en el interés de explotar el recurso eólico, este tipo de modelado podrá ayudar a predecir los efectos en los sistemas eléctricos y permitirá planear la compensación reactiva y el control de voltaje, usando controladores FACTS.
Configuraciones típicas de aerogeneradores
Los aerogeneradores usados para el aprovechamiento de la energía del viento se clasifican de varias formas. Entre las más usuales se encuentran:
– Por el tipo de construcción y funcionamiento. Síncronos o asíncronos
– Por su velocidad. Velocidad fija o velocidad variable.
Entre las configuraciones típicas de los aerogeneradores se encuentran las mostradas en la figura 1.
En la figura 1 se muestra en algunos casos la compensación de potencia reactiva como parte de un sistema individual; sin embargo, es factible tener un compensador de potencia reactiva centralizado (Ackerman, 2005; Fernández, 2009).
Modelado del generador eólico
El modelado básico de un aerogenerador consta de cuatro partes, el simulador de velocidad de viento, la turbina eólica con su caja de engranes, el generador con su compensación individual (opcional) y la red eléctrica a la cual estará interconectado (Abo–Khalil et al., 2006). En caso de no tener compensación entregará la potencia activa y tomará de la red la potencia reactiva, como se ve en la figura 1(a), donde se muestra un aerogenerador de inducción conectado directamente a la red eléctrica.
El presente trabajo presenta un modelo basado en el esquema presentado en la figura 1(b), donde un generador de inducción es conectado a la red y una compensación de potencia reactiva fija es aprovisionada a fin de suministrar los requerimientos del generador. Los generadores de inducción son comúnmente usados por su robustez, confiabilidad y eficiencia. También presentan una buena relación costo–eficiencia por la facilidad de construirlos en masa. Comparados con los generadores síncronos, los generadores de inducción tienen la ventaja de no necesitar excitación de campo y no requieren sincronización (Dorrell, 2004).
Los generadores de inducción a velocidad fija son automáticamente controlados y producen electricidad a una frecuencia constante. Sin embargo, su aplicación en turbinas eólicas se ve afectada por la variabilidad del viento, de tal manera que éstas deben ser diseñadas para obtener una mayor eficiencia (Burton, 2001). Diferentes métodos de control de velocidad pueden ser aplicados.
La meta del modelo es calcular la potencia activa proporcionada por el generador eólico, dados los valores medidos de velocidad del viento y su dirección (Ackerman, 2005), así como la potencia reactiva en función de la potencia activa y el voltaje de conexión.
La potencia activa producida por una turbina se expresa por la siguiente ecuación,

donde:
P es la potencia activa en watts,
ρ la densidad del aire en Kg/m3,
A el área del rotor en m2 y
Cp el coeficiente de potencia o eficiencia del rotor, el cual está en función de P y X,
β este parámetro, es el ángulo de paso (pitch angle) y
λ es conocida como relación de velocidad periférica (TSR) y se representa por la ecuación,

donde:
Wt es la velocidad de la turbina en rad/s,
R el radio de la turbina en m,
v la velocidad del viento en m/s.
La curva de potencia de los aerogeneradores es suministrada por los fabricantes y proporciona información adicional, como el inicio y paro de generación de la turbina. De esta curva se obtiene el Cp y entonces la ecuación (1) se simplifica como

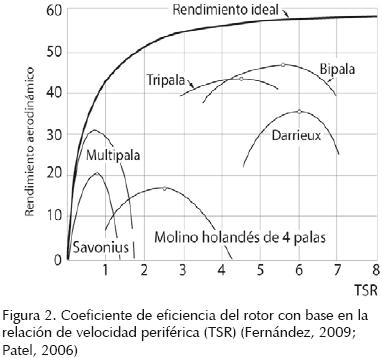
El coeficiente de potencia puede alcanzar un valor teórico máximo de 0.59, que es el llamado límite de Bete, aunque en la práctica este valor para turbinas de más de dos palas alcanza hasta 0.47 (Fernández 2009; Patel, 2006). La figura 2 muestra curvas características del Cp.
Para mostrar la relación entre la velocidad y la potencia producida, una muestra de un mes de mediciones tomada en una estación monitora del estado de Zacatecas es usada y se está suponiendo una central eoloeléctrica de 12 turbinas con capacidad de 2500 kW cada una. Las contribuciones de cada una de las turbinas se suman en cada intervalo medido para obtener la curva de la potencia total de la central eólica.
De la figura 3 se observa que por debajo de la velocidad de arranque del generador de 4.5 m/s, las turbinas no producen potencia, mientras que cuando la velocidad alcanza la tasa de generación a una velocidad de 8.5 m/s la curva de potencia se achata en un valor de 30 MW (12 turbinas de 2.5 MW c/u), la velocidad de paro (25 m/s) no se alcanza en este periodo de muestra.
Requerimientos de potencia reactiva
Como se mencionó anteriormente, los generadores de inducción requieren compensación reactiva. Los requerimientos de potencia reactiva de la central dependerán del tipo de aerogenerador utilizado. La relación entre potencia activa y reactiva se determina por el diseño, la potencia entregada y el voltaje nodal. Los bancos de capacitores o fuentes de potencia reactiva son añadidos de manera individual a los aerogeneradores con la finalidad de suministrar el déficit de potencia reactiva localmente, sin necesidad de importarla de otras partes de la red con sus respectivos problemas.
Usando el modelo de estado estable de una máquina de inducción y aplicando el teorema de Boucherot (Feijoo et al., 2000), la siguiente expresión puede usarse para calcular la potencia reactiva consumida por el generador,

donde:
V es el voltaje,
P la potencia activa,
X la suma de las reactancias del estator y el rotor,
Xc la reactancia del banco de capacitores,
Xm la reactancia de magnetización y
R la suma de las resistencias del estator y el rotor.
De la ecuación anterior, se considera que ambas potencias, activa y reactiva fluctuarán en función de la velocidad del viento, ya que la potencia activa depende de dicha velocidad. La figura 4a muestra una gráfica de la relación típica entre potencia activa generada y potencia reactiva absorbida por un generador de inducción y se observa que el generador requiere proporcionalmente más potencia reactiva cuando entrega más potencia activa. En la figura 4b se muestra el perfil de potencia reactiva que la central eólica modelada absorbería.
Ante esta situación, ambas potencias pueden ser conocidas (ecuaciones 3 y 4) mediante el generador modelado como un nodo PQ para análisis de flujos de potencia (Feijoo et al., 2000).
Integración de la central eólica a una red eléctrica
La inclusión de una fuente variable de potencia como la eólica en un sistema eléctrico, afecta el control del mismo. La generación tradicional intenta seguir la fluctuación de la curva de demanda para minimizar las variaciones de voltaje y corriente. Una cierta cantidad de generación es puesta en línea, lista para usarse en la compensación de estas fluctuaciones de carga, esta potencia es denominada "reserva rodante". La incorporación de grandes cantidades de potencia eólica en un sistema incrementa las variaciones en periodos cortos de la carga en comparación con generación tradicional, esto incrementa la necesidad de "reserva rodante" en los sistemas. También afecta las cargas principales interfiriendo los planes de despacho energético debido a las variaciones de la velocidad del viento.
La penetración de energía eólica puede definirse como la relación de la potencia instalada contra la máxima carga del sistema. Hoy en día, pocos países han alcanzado una penetración más allá del 10%. Aunque se estima que con tecnologías adicionales un 50% podría ser factible (Van Hulle et al.,2009).
La solución de flujos de potencia consiste en resolver un grupo de ecuaciones algebraicas que describan la red eléctrica bajo condiciones de estado estable. El programa desarrollado es adecuado para resolver redes pequeñas y de mediano tamaño y se realiza a partir del programa de flujos de potencia presentado en el libro: "FACTS: Modelling and Simulation in Power Networks" (Acha et al., 2004). El modelo propuesto para la turbina es incorporado al programa. Las potencias activa y reactiva de las turbinas son sumadas y se usan para modelar la central como un nodo PQ. Las ecuaciones de desajuste son establecidas y las variables de cada nodo son calculadas. El nuevo valor de la magnitud de voltaje se considera para calcular la potencia reactiva según la ecuación (4) y el algoritmo se repite hasta alcanzar una convergencia de 1e–12 p.u., en cada periodo de tiempo.
Para estudiar el efecto de la potencia activa generada e inyectada por la central eólica a una red, así como sus requerimientos de potencia reactiva, se usa una red de cinco nodos, siete líneas de transmisión y cuatro cargas. Un algoritmo de flujos dinámicos de potencia utilizando el método Newton–Raphson (Acha et al., 2004), ha sido desarrollado y programado en Matlab®.
Caso de estudio
Esta sección presenta los resultados obtenidos, usando el modelo propuesto de una central eólica, donde los efectos causados al conectar una central eólica a la red eléctrica compuesta por 5 nodos, son mostrados. En las simulaciones realizadas se utilizaron cantidades por unidad (p.u.). El programa desarrollado toma un máximo de cinco iteraciones para converger en cada uno de los 4032 diferentes estados. La carga total del sistema se mantiene constante a 165 MW y 40 MVAR de potencia activa y reactiva, respectivamente. El nodo North es considerado el "Slack" y presenta una magnitud de voltaje constante de 1.06 p.u. en todo el periodo analizado. La línea que conecta los nodos "Main" y "Elm" es abierta para conectar la central eólica a un nuevo nodo "Wind". La potencia activa inyectada y reactiva absorbida durante el periodo son las que se muestran en las figuras 3 y 4, respectivamente. Para el presente estudio la penetración máxima de potencia eólica es de aproximadamente un 15.15% (Van Hulle et al., 2009). La figura 5 presenta la red de pruebas utilizada en el estudio con dos soluciones particulares, (a) con cero generación eólica y (b) con máxima generación eólica (30 MW). La tabla 1 muestra los voltajes nodales en magnitud y ángulo de fase para ambos casos.


De la figura 5, es claro que en condiciones extremas, la potencia inyectada por la central eólica deja de ser transmitida por el sistema y ésta es ahora suministrada muy cercana a un centro de consumo. Lo anterior, permite que las pérdidas globales de transmisión se reduzcan, en este caso se observa que sin generación eólica las pérdidas alcanzan los 6.12 MW, mientras que con máxima generación eólica se reducen a 4.66 MW. El suministro extra de potencia, además implica que en algunas líneas de transmisión se incrementa su flujo de potencia, mientras que en otras líneas se reduce, y en algunas incluso se invertirá el sentido de los flujos de potencia que circulan sobre ellas. Desde esta perspectiva se logra observar que todas las líneas reducen la potencia activa transmitida, excepto las líneas "Wind–Elm", que incrementan el flujo de potencia activa de 6.60 MW a 19.28 MW y la línea "Main–Wind", la cual invierte el sentido, esto es, pasa de 6.60 MW, fluyendo de "Main" hacia "Wind" con un flujo de 10.65 MW de "Wind" hacia "Main". Como era de esperarse, la demanda de potencia reactiva del sistema se incrementa, dado que el modelo considera únicamente una compensación local para los aerogeneradores de 70%.
Para el espectro total de inyecciones de potencia activa del estudio, los resultados muestran que en la presencia de potencia eólica, los voltajes tienden a mejorar en toda la red. La figura 6 muestra los perfiles de voltaje nodales correspondientes a las inyecciones de potencia. De ésta, es fácil observar que los voltajes en los nodos de carga y el propio de conexión son afectados positivamente por las variaciones de la velocidad del viento, únicamente los nodos "North" (nodo libre) y "South" (nodo PV) no son afectados, manteniéndose ambos todo el tiempo con sus valores nominales de 1.06 y 1.0 en p.u., respectivamente. Los demás nodos durante el estudio no rebasan los límites de voltaje (± 6%).

De igual manera para el espectro, las líneas de transmisión presentan un comportamiento fluctuante en función de la velocidad del viento. La figura 7 muestra los flujos de potencia en el tiempo para las ocho líneas de transmisión del sistema; asimismo, puede observarse que las ocho líneas en general reducen la transmisión de potencia activa. Sin embargo, la línea "Wind–Elm" incrementa el flujo cuando la inyección de potencia aumenta, mientras que la línea "Main–Wind" presenta una situación más crítica, pues se observa que presenta varios cruces por cero en la gráfica, hecho que se interpreta como cambios en el sentido del flujo de potencia. Los cambios de sentido de flujo deberán ser considerados en el diseño de dicha línea.

Al usar fuentes de energía renovable, tales como la energía eólica, la emisión de contaminantes a la atmósfera se reduce considerablemente. Se considera que las plantas eólicas emiten un valor promedio de 7.4 toneladas de CO2 por GWh producido (Merino, 2009), y en algunos casos se considera con valores cercanos a cero (Spadaro et al., 2000).
En el caso del estudio presentando datos de un mes, la potencia total entregada durante este periodo es de 6.414 GWh, de tal manera que a razón de 7.4 toneladas de CO2/GWh, representaría una reducción de 6739.83 toneladas de CO2 en un mes y 80877.96 toneladas de CO2 en un año, si se usara una planta generadora que utilice carbón como combustible. La tabla 2, presenta una comparación de emisiones entre plantas convencionales de generación.
Observamos en la tabla 2 que la diferencia de emisiones de CO2 es enorme. Esto es una muestra de los beneficios que se obtienen al utilizar la energía del viento.
Conclusiones
El modelo de la central eólica aquí presentado, calcula la potencia activa de cada turbina en función de la curva de velocidad del viento, obtenida en una estación monitora del estado de Zacatecas, México. Las simulaciones para la incorporación de una central eólica en la red, muestran que este tipo de generación distribuida puede utilizarse tanto para compensar el voltaje en áreas remotas de las redes, como para suministrar localmente potencia activa. Las pérdidas por transmisión también pueden reducirse, dado que ahora menos potencia tendrá que ser transmitida por largas distancias. El modelo de generador de inducción actúa como su propio compensador, absorbiendo mayor potencia reactiva cuando la magnitud de voltaje se incrementa. El incremento de la capacidad de generación de la central, aumentará las variaciones de la magnitud de voltaje en el nodo de conexión y sus nodos vecinos. Los nodos de voltaje controlado (PV) en la red, deberán absorber o inyectar cantidades variables de potencia reactiva con el fin de lograr la compensación de voltaje programada. Incrementar la capacidad de los sistemas de compensación individual de las turbinas, permitirá obtener una mayor cantidad de potencia reactiva fija local, esto mejorará los perfiles de voltaje de los nodos cercanos a la central eólica y atenuará la generación de reactivos en los nodos libres y tipo PV.
El trabajo futuro en el modelado de centrales eólicas embebidas a sistemas eléctricos, deberá incluir modelos de redes más realistas con modelos de cargas más detallados. El efecto de las centrales en las redes debe ser evaluado de tal manera que la selección del sitio de instalación sea optimizada en función de los parámetros de la red eléctrica, cuando esto sea posible. El modelado de diversas fuentes de compensación debe realizarse, incluyendo controladores FACTS. Este tipo de simulaciones ayuda a entender la interacción dinámica entre las centrales eólicas y las redes eléctricas y facilitar la evolución hacia un uso más generalizado de las energías renovables.
Agradecimientos
El primer autor agradece el apoyo económico otorgado por DGAPA mediante proyecto IN116108 para la realización del presente proyecto.
El segundo autor agradece el apoyo a la UAZ y al PROMEP, su apoyo para la realización del presente trabajo.
Referencias
Abo–Khalil A.G, Lee D. Dynamic Modeling and Control of Wind Turbines for Grid Connected Wind Generation System. On: Power Electronics Specialists Conference, 2006. PESC '06. 37th IEEE Publication, pp. 18–22, June 2006. [ Links ]
Acha E, Fuerte–Esquivel C.R., Ambriz–Pérez H., Angeles–Camacho C. FACTS: Modelling and Simulation in Power Networks. En–gland.John Wiley & Son. 2004. [ Links ]
Ackerman T. Editor. Wind Power in Power Systems. Second Edition. USA. John Wiley and Sons. 2005. [ Links ]
Angeles–Camacho C. Phase Domain Modelling and Simulation of Large–scale Power Systems with VSC–based FACTS Equipment. Tesis (for the degree of PhD) Scotland University of Glasgow. 2005. [ Links ]
Burton T. et al. Handbook of Wind Energy. England. John Wiley and Sons Ltd. 2001 [ Links ]
Dorrell D. Course Notes for the M.Sc. Module in Electrical Energy Systems. Scotland. University of Glasgow. 2004. [ Links ]
Feijoo A.E., Cidras J. Modelling of Wind Farms in the Load Flow Analysis. IEEE Trans. On Power Syst, 15:110–115. 2000. [ Links ]
Fernández P. Energía eólica. España [en línea]. Universidad de Cantabria. [fecha de consulta 08 de abril 2009]. Disponible en: http://libros.redsauce.net/EnergiasAlternativas/eolica/PDFs/EOLO42002.pdf [ Links ]
Merino L. Energías renovables. Colec. Energías renovables para todos. España. [en línea]. Haya Comunicación. [fecha de consulta 18 de junio 2009]. Disponible en: http://www.energias–renovables.com/Productos/pdf/cuaderno_GENERAL.pdf [ Links ]
Patel M.R. Wind and Solar Power Systems: Design Analysis and Operation. 2nd ed.Florida (USA). CRC Press. 2006. [ Links ]
Slootweg J.G., Kling W.L. Modelling and Analysis Impacts of Wind Power on Transient Stability of Power Systems. Wind Engineering 25. 2001.Pp. 3–20. [ Links ]
Spadaro V, Langlois L, Hamilton B. Greenhouse Gas Emissions of Electricity Generation Chains: Assessing the Difference. IAEA Bull, 42(2). 2000. [ Links ]
Van Hulle F., Gardner P. Grid Integration Part 2: Wind Energy Penetration and Integration. [en línea]. [fecha de consulta 08 de abril 2009]. Disponible en: http://www.wind–energy–the–facts.org/es/part–2–grid–integration/chapter–1–setting–the–scene/wind–energy–penetration–and–integration.html [ Links ]
Semblanza de los autores
César Angeles–Camacho. Obtuvo el grado de licenciado y maestro en ingeniería por el Instituto Tecnológico de Morelia, México, en 1992 y 2000, respectivamente. En 2005, obtuvo el grado de doctor por la Universidad de Glasgow, Escocia. Se unió al Instituto de Ingeniería de la Universidad Nacional Autónoma de México en 2005 como investigador. Sus intereses de investigación incluyen el modelado y simulación de FACTS y controladores para la calidad de potencia.
Francisco Bañuelos–Ruedas. Obtuvo el título de ingeniero mecánico electricista en 1983 y el grado de maestro en ingeniería eléctrica en 2004 por la UNAM. Es profesor investigador de la Universidad Autónoma de Zacatecas. Actualmente estudia el doctorado en el área de sistemas energéticos de la Facultad de Ingeniería de la UNAM y está adscrito como becario–estudiante del Instituto de Ingeniería de la UNAM.














