Introducción
En ingeniería, el fenómeno de la cavitación se define como la formación y crecimiento de burbujas en un flujo cuando el líquido alcanza su presión de vapor y sus posteriores colapsos cuando se recupera la presión (Franc & Jean, 2005). La presencia de estas burbujas induce oscilaciones en el flujo y vibraciones debido a los cambios volumétricos que sufren. Existen modelos matemáticos que relacionan la frecuencia de las oscilaciones con la geometría esférica inicial (Plesset & Prosperetti, 1977) y la asimetría de las burbujas (Longuet & Michael, 1989). A partir de los modelos anteriores, se proponen diversos modelos teóricos analíticos y numéricos, que consideran tanto parámetros físicos como químicos para estudiar el fenómeno denominado “cavitación hidrodinámica” como los de Brennen (1995), Gonçalves et al. (2001), Gastona et al. (2001), Kyuichi et al. (2010) y Gnanaskandan & Mahesh (2015). De acuerdo con los resultados presentados en los trabajos anteriores, en términos generales, los efectos macroscópicos del flujo son función de la energía contenida en las burbujas.
Tanto los modelos de la mecánica clásica como los fisicoquímicos se complican considerablemente al escalar el fenómeno para aplicaciones de ingeniería. En consecuencia, las teorías de parámetros concentrados adquieren importancia al aproximar el comportamiento dinámico de las burbujas inspeccionando los parámetros macroscópicos del sistema (Hidráulicos). Basándose en este concepto, Louis (1940) establece la primera matriz de transferencia dinámica para flujos ideales y estacionarios. En años posteriores, D’Souza & Oldenburger (1964) establecen la función de transferencia para redes hidráulicas con tuberías cilíndricas, usando las ecuaciones de Navier-Stokes y la transformada de Laplace. Concluyendo que en los flujos de comportamiento oscilante, superiores a 102 Hz, es factible despreciar los efectos de la viscosidad y fricción de las paredes.
Aunque el método de parámetros concentrados se ha utilizado desde 1940, son Brennen & Acosta (1973), (1975) y (1976), los primeros en modelar la cavitación hidrodinámica, en una bomba hidráulica, parametrizando en un coeficiente resistivo, capacitivo e inductivo. Estableciendo así el factor de ganancia de flujo másico, causado por la producción fluctuante de burbujas. En trabajos posteriores como Brennen (1978) y (2007) se introdujo un factor de acoplamiento que considera la inercia de la bomba, del flujo y la concentración de las burbujas. Permitiendo estudiar el estado transitorio de los flujos y demostrando que la producción fluctuante de las burbujas genera ondas de presión cinemáticas y dinámicas que superan los límites de diseño. Basándose en los trabajos anteriores, Yamamoto & Tsujimoto (2009) desarrollan un modelo de balance de energías y otro en parámetros concentrados de un circuito hidráulico que consta de una bomba hidráulica, una válvula y tanques de almacenamiento. En su trabajo muestran que la estabilidad del conglomerado de burbujas está relacionada con el valor negativo del factor de ganancia de flujo.
Modelos como el de Ashok et al. (2002) están ya disponibles en códigos computacionales para determinar, con ligeras consideraciones, la histéresis del módulo volumétrico del flujo y la densidad en el proceso de compresión y descompresión de una mezcla. Tal es el caso de Junjie et al. (2013) quien determina el modulo volumétricos y la densidad transitoria en un pistón hidráulico. Otros modelos teóricos para estudiar el régimen transitorio, mediante parámetros concentrados, son los de Donghyuk & Kazuhiko (2014), Shihua et al. (2015) y Kamil & Zbigniew (2015). Estos modelos permiten determinar la frecuencia de operación, histéresis, factor de pérdidas, calidad, tiempo de respuesta, factor de ganancia y estabilidad.
Son Zuo et al. (2006) quienes al estudiar la impedancia de un sistema hidráulico con un tubo Venturi, asocian el comportamiento colectivo de las burbujas con las presiones dinámicas de bajas frecuencias (<102 Hz). En ese mismo año, Li et al. (2006) determinan que para un sistema hidrodinámico semejante al anterior, las fases del flujo tienen frecuencias propias que se acoplan mediante la velocidad de flujo. En años posteriores, Zuo et al. (2009) demuestra además que las oscilaciones volumétricas de un conglomerado de burbujas en un Venturi tienen las mismas frecuencias que las oscilaciones de presión. Siguiendo los trabajos anteriores Cruz & Navarrete (2016) demuestran teóricamente que la frecuencia de oscilación de los conglomerados de burbujas es una función de las características de su población, la geometría del tubo Venturi y la fracción volumétrica de gas y vapor disuelta.
Debido a lo anterior, en este trabajo se estudia en forma teórica y experimental el flujo cavitante a través de un tubo Venturi. Se aplica un enfoque matemático en parámetros concentrados, partiendo de las ecuaciones de conservación de flujos (masa y momento) junto con las analogías eléctrica e hidráulica. Así se establecen los coeficientes locales de capacitancia, inductancia y frecuencia. Este último coeficiente es dependiente tanto de la geometría del tubo Venturi como del número de cavitación, Mach y la fracción volumétrica de la fase gaseosa. Experimentalmente se observa la disminución del contenido espectral, que se determina teóricamente, al incrementar el caudal y así el número de Mach y la fracción volumétrica de la fase gaseosa.
Modelo teórico
Es factible modelar un sistema dinámico mediante parámetros concentrados cuando la dependencia espacial de las variables no se considera, es decir, cuando un cambio en las variables es igual y simultáneo en todo el volumen de estudio (Benson & Benson, 1991). Se considera un flujo estacionario bifásico, homogéneo, unidimensional y barotrópico con una fase líquida newtoniana y una mezcla ideal de vapor y gas, denominada desde ahora como fase gaseosa. Además, no existe transferencia de calor y masa entre las fases. El flujo pasa a través de un tubo Venturi con la geometría mostrada en la Figura 1.
Como sabemos, todo sistema se modela mediante estados a partir de las ecuaciones que
rigen su dinámica. Dos estados son fundamentales en el análisis de los sistemas
dinámicos, concentración y disipación de energía. Para modelar estos estados, se
usan los coeficientes capacitivo C, inductivo L y
resistivo R, así como las principales variables que constituyen una
analogía entre los sistemas eléctricos e hidráulicos. Donde la intensidad de
corriente i es análoga con el flujo másico
Tabla 1: Analogía entre sistemas eléctricos e hidrodinámicos, donde
| Sistema Eléctrico | Sistema Hidráulico |
|---|---|
|
|
|
|
|
|
|
|
|
Los facvtores geométricos del volumen de control y las propiedades del flujo están contenidos en los coeficientes C, L y R. El coeficiente capacitivo c se asocia al cambio volumétrico de las fases, el inductivo L a la caída de presión que acelera el flujo y el resistivo R al amortiguamiento generado por la viscosidad del flujo.
Coeficiente capacitivo
Se aplica la siguiente ecuación de continuidad bifásica para flujos confinados (Brennen C., 2005)
donde
Note que en la Ecuación (2) el
donde α, P y γ son la fracción volumétrica de la fase gaseosa, la presión local y el índice politrópico del gas, respectivamente. Sustituyendo la Ecuación (3) y la velocidad del sonido en el líquido en la Ecuación (2) e integrando, respecto de x, se obtiene la siguiente expresión
La ecuación anterior es válida cuando los cambios de presión como una función del tiempo son predominantes. Esta condición se logra cuando la generación de ondas de presión se suma a la caída de presión permanente ocasionada por los factores geométricos.
Dado que
donde la caída de presión
Multiplicando y dividiendo la Ecuación (5) por el cuadrado de la velocidad media del flujo u2 y por el cuadrado de la velocidad del sonido en el flujo a2, la Ecuación (5) se reescribe como
donde σ y M son el número de cavitación y Mach, respectivamente.
Coeficiente inductivo
Se usa la siguiente ecuación de movimiento para flujos sin fricción (Brennen, 2005)
donde
Note que el parámetro inductivo solo depende de los factores geométricos del tubo Venturi, de acuerdo con las consideraciones.
Coeficiente de frecuencia
Se determina a partir de la expresión de frecuencia de un sistema de segundo orden, por su capacidad de emitir y amortiguar frecuencias (Ecuación (9)).
Sustituyendo las Ecuaciones (6) y (8) en (9) se obtiene la siguiente expresión
donde
donde
Arreglo experimental
En la Figura 2, se esquematiza el circuito hidráulico a utilizar por el cual fluye agua sin ningún tratamiento previo. Cuenta con un tanque de refrigeración capaz de mantener una temperatura máxima de 33 °C en régimen de cavitación desarrollada, una bomba de 5 Hp controlada por un convertidor de frecuencia que asegura un ajuste de la tasa de flujo del líquido, una válvula de regulación de gasto, válvula de purga, dos válvulas de paso, un manómetro diferencial de mercurio y un tanque de almacenamiento 70 L. La tubería es de PVC (policloruro de vinilo) de 50.8 mm de diámetro, cédula 40 y 80, así bien, el tubo Venturi es manufacturado en PMMA (Polimetacrilato de metilo). Para monitorear los cambios en frecuencia se aplica un golpe con un sensor de fuera, en caída libre, al tubo Venturi y las señales generadas son censadas con un transductor piezoeléctrico de 1 MHz de ancho de Banda. La temperatura se monitorea con un termopar tipo J en el tanque de almacenamiento. Finalmente la cámara de alta velocidad se programa para adquirir 49,000 cuadros por segundo del tubo Venturi.
Resultados y discusión
El presente modelo teórico se aplica entre la entrada de la zona convergente y garganta del tubo Venturi, ya que en estas zonas la presión del flujo puede caer hasta la presión de vapor del líquido y generar una mezcla bifásica (Figura 1). Este flujo cavitante se considera una mezcla de agua y vapor de agua a 25 °C y sus propiedades físicas se muestran en la Tabla 2. Dos casos de estudio se consideran en la parte teórica:
Tabla 2: Propiedades físicas del agua a 25 oC
| Velocidad del sonido | 1542 m/s |
|---|---|
| Densidad | 989 kg/m3 |
| Velocidad del sonido (vapor de agua) | 443 m/s |
| Densidad de vapor | 0.083 kg/m3 |
| Índice politrópico | 1.4 |
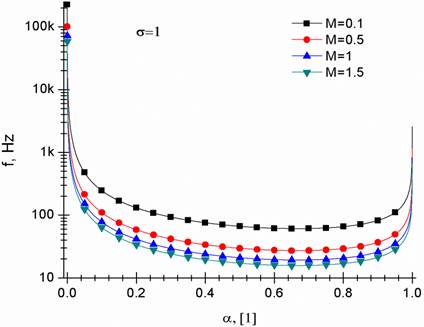
Figura 3: Comportamiento del coeficiente de frecuencia de un flujo cavitante en agua como una función de la fracción volumétrica de la fase gaseosa α y el número de Mach M. Considerando un número de cavitación σ=1
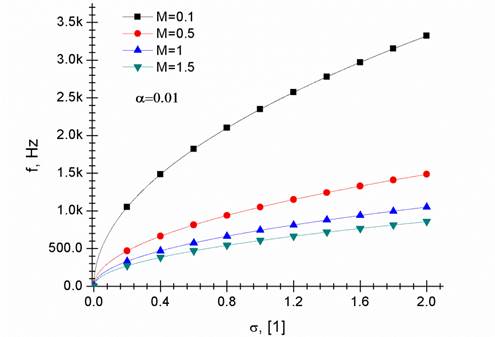
Figura 4: Comportamiento del coeficiente de frecuencia de un flujo cavitante de agua como una función del número de cavitación σ y del número de Mach M. Considerando una fracción volumétrica α=0.01. Donde se observa que el incremento de M y el decremento de σ disminuyen la magnitud del coeficiente de frecuencia
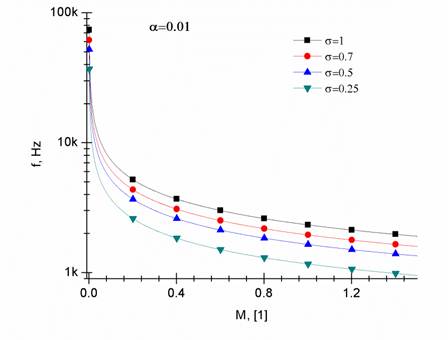
Figura 5: Comportamiento del coeficiente de frecuencia como una función del número de Mach con una fracción volumétrica de fase gaseosa constante α
Los datos de la caída de presión se adquieren entre la entrada de la zona convergente y garganta del tubo Venturi desde una condición subsónica y a diferentes temperaturas iniciales (Figuras 6 y 7).
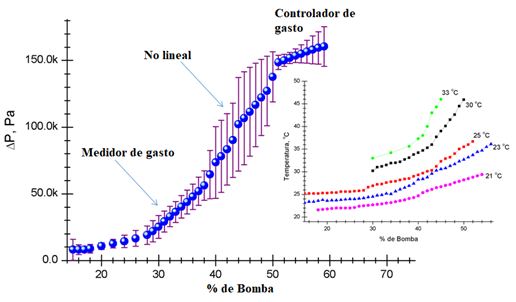
Figura 6: Comportamiento de la caída de presión y temperatura como una función del porcentaje de trabajo de la bomba hidráulica
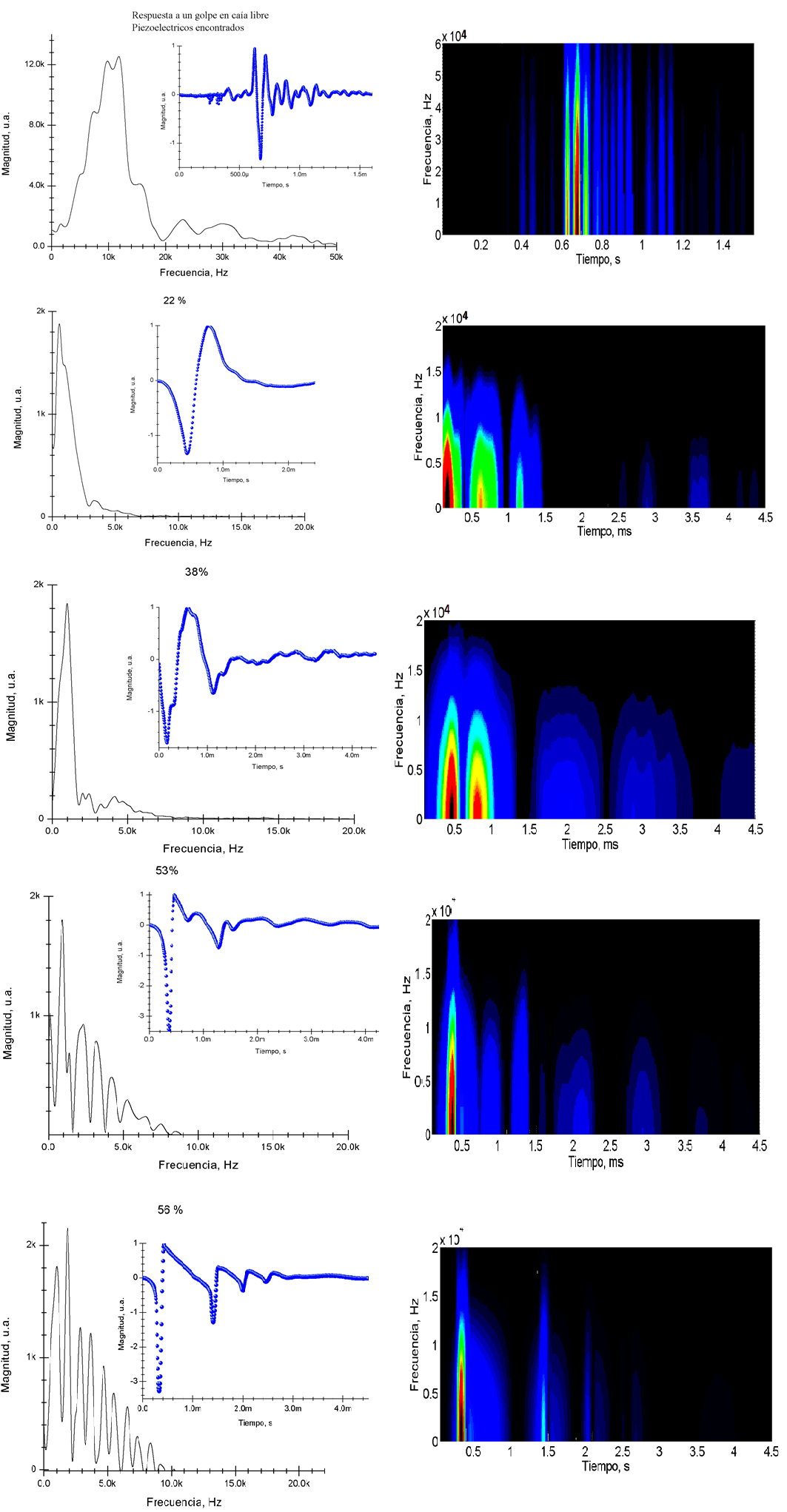
Figura 7: Análisis en tiempo y frecuencia de la respuesta generada por un sensor de fuerza en caída libre a un tubo Venturi cavitante. Las señales fueron adquiridas a diferentes porcentajes de trabajo de la bomba hidráulica y con una temperatura inicial de 33 °C. Donde u.a. significa unidades adimensionales
En la Figura 3 se observa que los flujos con una
fracción volumétrica gaseosa cercana a cero transmiten ondas de presión con
frecuencias tan altas como 10 KHz. Por el contrario, los flujos bifásicos
La Figura 4 muestra el comportamiento decreciente de la frecuencia al disminuir el número de cavitación. Este comportamiento se observa por Li et al. (2006) al estudiar la cavitación del Warwick Venturi. No obstante, tanto la Figura 4 como la Figura 3 sugieren además que los números de cavitación y Mach establecen las frecuencias que serán amortiguadas en el flujo cavitante.
En la Figura 5 se despliega el comportamiento en
frecuencia como una función del número de Mach, con 10% de fase gaseosa o
En la Figura 6 se despliega la caída de presión entre la entrada de la zona convergente y la garganta del tubo Venturi (Figura 1), así como el incremento en la temperatura. Donde se observa que a bajos porcentajes de trabajo de la bomba hidráulica (<40%), se presenta un comportamiento casi lineal con ligeras desviaciones estándar. Este comportamiento nos sugiere que sin importar la temperatura inicial del líquido, es factible estimar el caudal con el tubo Venturi a bajas velocidades de flujo. Al incrementar el porcentaje de trabajo de la bomba, de 40 a 50%, aumenta también la desviación estándar, ya que se generan variaciones de presión por los colapsos colectivos de burbujas. Un comportamiento similar se observa para porcentajes de trabajo mayores a 50%, por lo que, el comportamiento del tubo Venturi como controlador de gasto es dependiente también de la temperatura.
En la Figura 7 se muestran los espectros en frecuencias y espectrogramas de un golpe dado por el sensor de fuerza al tubo Venturi. Inicialmente se muestra la respuesta del sensor de fuerza y el piezoeléctrico de recepción encontrados, donde se observa una densidad espectral de hasta 60 kHz. Al montar el instrumento en el tubo Venturi y dar un golpe a 22% de trabajo de la bomba hidráulica, la magnitud y la frecuencia disminuyen considerablemente debido a la separación entre los transductores y a la fracción volumétrica gaseosa inicial. Alrededor de un 38% de trabajo de la bomba hidráulica, el contenido espectral disminuye, indicando que el número de Mach aumentó por el incremento de la velocidad del flujo. Finalmente, en un 53% de trabajo de la bomba hidráulica se amortiguan algunas frecuencias generadas por el golpe del sensor de fuerza y aparecen otras que no se observan en las condiciones anteriores. Un comportamiento similar se observa en un 56% de trabajo, pero las frecuencias que aparecen muestran mayor magnitud. Esto sugiere que se generan ondas de presión que se superponen con la señal del golpe y son detectadas por el transductor piezoeléctrico de recepción. Además, a mayor potencia suministrada al flujo, mayor será la cantidad e intensidad de las ondas de presión generadas.
La Figura 8 muestra un ciclo del comportamiento
dinámico del flujo bifásico, en la zona divergente, a 56% de la potencia de bombeo.
La imagen: a) ilustra la fracción volumétrica gaseosa (una sola estructura) que
llena toda la garganta y una parte de la zona divergente. En b) se muestra un zoom
de la zona divergente y c) muestra una nube de burbujas que se separó de la única
estructura de cavitación por una onda de presión que se generó. Esta nube de
burbujas se mueve a través de la zona divergente hasta una posición donde colapsa
emitiendo una segunda onda de presión (ver d)), que posiblemente en su origen haya
sido una onda de choque (ver e)). Desde f) hasta i) se observa cómo la onda de
presión se propaga en el flujo. De acuerdo con las imágenes adquiridas por Pavel et al. (2014), para un
sistema similar al nuestro, se estableció que el régimen del flujo cavitante
presente en el tubo Venturi es del tipo parcial. Esto nos permite determinar un
intervalo de números de cavitación
Conclusiones
Se establecieron los coeficientes locales de inductancia, capacitancia y frecuencia para flujos estacionarios bifásico, homogéneo y unidimensional. El coeficiente de frecuencia es dependiente de la geometría del tubo Venturi, la fracción volumétrica de la fase gaseosa, los números de Mach y cavitación. Debido a que la frecuencia depende de las variables anteriormente mencionadas, es factible utilizarlo en futuros trabajos para determinar la presencia y el régimen de cavitación. Con base en el modelo establecido, se determinó que los flujos con un régimen de cavitación parcial amortiguan frecuencias superiores a 10 KHz. Así bien, es posible que cada régimen cavitante amortigüe un determinado intervalo de frecuencias, ya que las principales variables que activan esta condición son el número de Mach y cavitación. Experimentalmente se demostró el amortiguamiento de las frecuencias generadas por el golpe del sensor de fuerza en caída libre a diferentes porcentajes de trabajo de bombeo. Mediante la cámara de alta velocidad se demostró la generación de ondas de presión que nos indica que el flujo cavitante dejo de amortiguar ondas de presión y comenzó a generarlas. Este comportamiento de los flujos cavitantes como generadores de ondas de presión no es predicho por el modelo teórico y será tratado en futuros trabajos.











 nueva página del texto (beta)
nueva página del texto (beta)






