1 Introducción

La industria farmacéutica representa al sector productivo dedicado a la fabricación de medicamentos utilizados en el tratamiento y/o prevención de las enfermedades (^{Salomon 2006}; ^{Brunton y col., 2011}; ^{Aulton, 2004}). Por su efecto en la salud, los resultados de las investigaciones de esta industria presentan una elevada importancia económica y social (^{Villanueva, 2003}; ^{McKenzie y col., 2006}). Es por ello, que el desafío consiste en la producción de medicamentos de reconocida calidad y elevada efectividad terapéutica, utilizando eficientemente los métodos modernos y las estrategias avanzadas de fabricación y control (^{Benitez y col., 2015}; ^{Rogers y Ierapetritou, 2015}).

El agua representa el recurso natural más importante del planeta Tierra (^{Gleick, 1993}; ^{Pedregal y col., 2009}; ^{Rivas-Perez, 1990}). En la industria farmacéutica, el agua de uso farmacéutico constituye la sustancia más utilizada (^{Lerín y col., 1999}; ^{Vila Jato, 2001}), y debe contar con una calidad consistente para cumplir con las buenas prácticas de fabricación y control (^{Collentro, 2011}). Para ello, se separan del agua potable los contaminantes (purificación del agua), mediante la utilización de diferentes tecnologías, entre las que se destacan: las técnicas de membranas, la nanofiltración y la ósmosis inversa (OI) (^{Pahwa y col., 2010}; ^{Belkacem y col., 2008}).

Actualmente, uno de los procedimientos más utilizados para la purificación de agua potable en la industria farmacéutica es la OI (^{Belkacem y col., 2008}), debido a que posibilita eliminar hasta el 98% de los contaminantes, con un coste relativamente bajo. Este procedimiento se desarrolla en las unidades de OI de las plantas purificadoras de agua potable, las cuales se caracterizan por presentar un comportamiento dinámico multivariable (MIMO). Para la producción de agua de uso farmacéutico de calidad consistente resulta necesario garantizar las condiciones óptimas de operación de la unidad de OI (en lo adelante planta) (^{Malaeb y Ayoub, 2011}). Por consiguiente, la aplicación de estrategias efectivas de control es fundamental para la obtención de una alta eficiencia con bajo coste de operación (^{Morales-Díaz y Carlos- Hernández, 2010}; ^{González-Lavaut y col., 2009}). Las investigaciones encaminadas a la reducción de coste y optimización de la operación en estas plantas, han sido desarrolladas esencialmente desde el punto de vista de la mejora de sus elementos básicos (bomba de alta presión y membranas) (Malaeb y Ayoub, 2011).

Para el control de las variables críticas de las unidades de OI se utilizan fundamentalmente controladores convencionales del tipo PI o P (^{Alatiqi y col., 1999}; ^{Bartman y col., 2009a}). Sin embargo, cuando los procesos son multivariables (MIMO) y/o las variables a controlar presentan comportamientos dinámicos complejos, estos controladores no son suficientes para garantizar las condiciones óptimas de operación (^{Åström y Hägglund, 2009}; ^{Castillo- Garcia y col., 2013}; ^{Feliu-Batlle y col., 2011}; Rivas-Perez y col., 2000), sobre todo, si el flujo de agua de alimentación es variable (^{Rivas-Perez y col., 2003}). Ello puede conllevar a que se origine un deterioro en las propiedades del agua de uso farmacéutico (proliferación de microorganismos), con riesgos para la vida humana. En algunos casos, la producción de agua purificada de calidad consistente disminuye debido al inevitable ensuciamiento de las membranas de las unidades de OI (^{Belkacem y col., 2008}).Cuando esto ocurre, los controladores convencionales obligan a la bomba de alta presión a aumentar el flujo de agua de alimentación, originando un aumento de la tasa de ensuciamiento y la prematura destrucción de las membranas, lo cual conlleva a un crecimiento en el consumo de energía, así como a paradas eventuales de la planta (Bartman y col., 2009a).

En las últimas décadas ha sido reportado el uso de controladores predictivos basados en modelos (CPBM) para el control eficiente de las unidades de OI (^{Abbas, 2006}; ^{Ali y col., 2010}; ^{Ali y Zafiriou, 1993}; ^{Assef y col., 1997}; ^{Li y col., 2012}; Moncada-Valerio y col., 2012; ^{Robertson y col., 1996}; ^{Sobana y Panda, 2014}, etc.). Ello se debe a que estos controladores reproducen el comportamiento de un operador experto en el control de un determinado proceso, y además posibilitan el control efectivo de plantas MIMO (^{Camacho y Bordons, 2012}; ^{Richalet y col., 1978}). Sin embargo, una parte importante de estos controladores ha sido fundamentalmente diseñada en base a paquetes (software) comerciales, los cuales constituyen herramientas de control complejas y cerradas, que no permiten conocer el tipo de algoritmo de control predictivo que se utiliza, así como reproducir o introducir modificaciones en el algoritmo de control, además presentan elevados precios en el mercado, por lo que en diversas plantas resulta imposible su aplicación (^{Mrosko y Miklovičová, 2012}; ^{Xi y col., 2013}).

Entre los controladores CPBM disponibles en el mercado, uno de los que muestra mayor aceptación es el controlador predictivo generalizado (GPC) debido a sus indiscutibles ventajas (^{Clarke y col., 1987}; ^{Camacho y Bordons, 2012}). Nótese, que la mayor parte de las aplicaciones que se reportan de este controlador es en plantas SISO debido a la complejidad matemática de su diseño para plantas MIMO. En (^{Rivas-Perez y Sotomayor-Moriano, 2014}) se reporta un trabajo previo de diseño de un GPC para el control de una unidad de OI de una planta purificadora de agua potable de una industria farmacéutica. No obstante, las principales deficiencias de este trabajo son las siguientes: se ofrece un modelo matemático multivariable de la unidad de OI, sin resolver el complejo problema de su obtención; el GPC diseñado no considera las variaciones de los parámetros dinámicos de la planta, las cuales se originan como resultado del ensuciamiento paulatino e inevitable de las membranas (^{Li y col., 2012}), por consiguiente su efectividad es limitada; no se realiza una propuesta de implementación del GPC diseñado; la conductividad del permeado que se logra es de 400 μs/cm, la cual no se corresponde con la del agua de uso farmacéutico de calidad consistente, cuya conductividad a 25°C debe ser inferior a 1.3 μs/cm (^{Bevilacqua, 1996}), por ende el agua que se obtiene no puede ser utilizada en la producción de medicamentos. Es por ello, que el diseño e implementación de controladores GPC multivariables para el control efectivo de esta clase de plantas, garantizando la calidad y el cumplimiento de las exigencias tecnológicas de operación, constituye un reto importante, así como un campo de investigación de elevado interés científico y económico (^{Singh y col., 2013}).

El principal objetivo de este trabajo consiste en el diseño y propuesta de implementación, basada en una PC industrial, de un GPC multivariable para el control de las variables críticas de una unidad de OI de una planta purificadora de agua potable de una industria farmacéutica, que posibilite la obtención de agua de uso farmacéutico de calidad consistente.

Las principales contribuciones de este trabajo consisten en: 1) la obtención de un modelo matemático multivariable de la planta objeto de estudios utilizando los métodos de subespacios para la identificación de sistemas dinámicos; 2) la determinación mediante experimentos de la variación de los parámetros dinámicos de la planta objeto de estudio debido al ensuciamiento paulatino e inevitable de sus membranas; 3) el diseño y propuesta de implementación basada en una PC industrial de un GPC multivariable con un módulo de identificación y reajuste de parámetros para el control de dicha planta, que garantiza el cumplimiento de las exigencias tecnológicas de operación, así como la producción de agua de uso farmacéutico de calidad consistente.

Este trabajo ha sido estructurado de la siguiente forma. En la Sección 2, mediante la aplicación de los métodos de identificación de sistemas dinámicos basadas en subespacios, se obtiene un modelo matemático multivariable de la planta objeto de estudio. En la sección 3 se desarrolla el diseño del GPC multivariable. En la Sección 4 se realiza una propuesta de implementación del GPC diseñado basada en una PC industrial y se exhiben los resultados de simulación del sistema de control considerando diferentes escenarios reales de operación industrial de dicha planta. Finalmente, en la última Sección, se ofrecen las conclusiones.

2 Modelo matemático multivariable de una unidad de OI

Los resultados presentados en este trabajo se basan en una unidad de OI de una planta purificadora de agua potable de los laboratorios AICA de la industria farmacéutica de Cuba, dedicada a la fabricación, preparación y comercialización de medicamentos para el tratamiento y prevención de diferentes enfermedades. En la Fig. 1 se exhibe el diagrama funcional de esta planta con sus diferentes componentes, entre los que se encuentran: computadora personal (PC) industrial, tarjeta de adquisición de datos multifunción (TADM), filtro de 50 μm, suavizadores, tanque de agua suavizada, bomba de relanzamiento, tanque de suministro de metabisulfito de sodio (Na₂S₂O₅), intercambiador de calor, tanque de suministro de soda cáustica (NaOH), bomba dosificadora, filtro de 5 μm, unidad de OI, módulos de electrodesionización (EDI) y tanque de agua purificada. La planta cuenta con transmisores de temperatura (TT), presión (PT), nivel (LT), conductividad (AT), flujo (FT) y pH (pHT), así como con indicadores de presión (PI), temperatura (TI) y flujo (FI). La PC industrial a través de la TADM recibe las señales de los sensores transmisores y envía las señales de control hacia los actuadores (válvulas de control y motores de las diferentes bombas).

Fig. 1 Diagrama de la planta purificadora de agua potable 

En la unidad de OI, mediante la bomba de alta presión, se impulsa el agua de alimentación (pretratada) a través de las membranas, las cuales posibilitan la separación de las partículas contaminantes contenidas en el agua potable. De esta forma, en la primera salida de las membranas se obtiene un flujo de agua purificada (permeado) y en la segunda - un flujo de agua con partículas no deseadas (rechazo). La temperatura del agua de alimentación de la unidad de OI debe ser de 25°C para evitar el crecimiento microbiológico. El agua purificada de uso farmacéutico se considera de calidad consistente, si a 25°C exhibe una conductividad inferior a 1.3 μs/cm (^{Bevilacqua, (1996)}). Esta conductividad se logra agregando soda cáustica al agua pretratada (ajuste de pH). Entre las variables críticas de la unidad de OI se encuentran: la presión y el pH del agua de alimentación, el flujo y la conductividad del agua purificada (permeado), así como el flujo y la presión del agua con partículas no deseadas (rechazo) ^{Medina San Juan (2000)}.

Estas variables se caracterizan por presentar un comportamiento dinámico multivariable con fuertes interacciones (^{Abbas, 2006}; ^{Alatiqi y col., 1989}; ^{Bartman y col., 2009b}), lo cual dificulta la obtención de modelos matemáticos adecuados como objetos de control mediante la aplicación de las herramientas de modelado (^{Rivas-Perez y col., 1994}).

El diseño de CPBM requiere disponer de modelos matemáticos que describan de forma precisa el comportamiento dinámico más relevante de las plantas a controlar (^{Camacho y Bordons, 2012}). En los últimos años, para la obtención de modelos matemáticos adecuados de plantas industriales complejas se vienen utilizando de forma exitosa las herramientas de identificación de sistemas (^{Ljung, 1999}; ^{Rivas-Perez y col., 2008}), las cuales representan un campo de investigación actual de creciente interés científico-técnico (ver por ejemplo: ^{Ljung (2010)}, ^{Mandloi y Shah (2015)}, ^{Mu y col. (2015)}, ^{Oomen y Bosgra (2012)}, ^{Rivas-Perez y col. (2014)}). El objetivo fundamental de la identificación de sistemas consiste en la obtención de modelos matemáticos simples y precisos de plantas industriales complejas sobre la base de las observaciones (mediciones) de sus variables de salida y entrada obtenidas en condiciones de funcionamiento real y teniendo en cuenta que estas mediciones se encuentran afectadas por ruidos, perturbaciones e incertidumbres (Ljung, 1999; Rivas-Perez y col., 2011).

En este trabajo, para la obtención de un modelo matemático multivariable del comportamiento dinámico nominal de la unidad de OI objeto de estudio se utilizan los métodos de identificación de sistemas dinámicos mediante subespacios (^{Van Overschee y De Moor, 1996}). Entre las ventajas de estos métodos se encuentran: posibilidad de obtener modelos matemáticos dinámicos confiables en espacio de estado de sistemas multivariables directamente de los datos de entrada-salida; demanda de carga computacional modesta comparada con la de los métodos tradicionales, tales como el método del error de predicción (PEM), especialmente cuando el número de estados y de salidas es grande; disponibilidad de algoritmos eficientes basados en la descomposición en valores singulares (SVD) incorporados en el toolbox de Matlab; no se requiere de procedimientos de optimización iterativos; etc.

El problema de la identificación de sistemas dinámicos mediante subespacios consiste en determinar las matrices A, B, C, D de coeficientes de dimensiones correspondientes del siguiente modelo en el dominio de tiempo discreto (^{Van Overschee y De Moor, 1996}):

(1)

donde y ϵ ℜ ^p es el vector de salida, u ϵ ℜ ^m es el vector de entrada, x ϵ ℜ ⁿ es el vector de estado del sistema, ω(k) y v(k) son secuencias de ruidos. Los parámetros desconocidos del modelo en espacio de estado de la Ec. (1) se encuentran contenidos en las matrices A, B, C, D.

Los algoritmos de identificación basados en subespacios se fundamentan en la ecuación:

(2)

donde Y, U son matrices de Hankel formadas con los datos experimentales de salida/entrada, X es la secuencia de estado, Γ es la matriz de observabilidad extendida y H es una matriz de Toeplitz formada con los coeficientes de Markov del modelo Ec. (1).

Una vez calculada la secuencia de estado, las matrices A, B, C, D se pueden obtener median la solución de un problema de regresión mínimo cuadrática lineal, representado por la expresión:

(3)

donde,

(4)

x- ϵ R ⁿ es la estimación del vector de estado.

La estimación mínimo cuadrática de Θ viene dada por:

(5)

Este procedimiento es conocido como el método directo de los algoritmos numéricos basados en subespacios para la identificación de sistemas dinámicos en espacio de estados (N4SID), desarrollados por ^{Viberg y col. (1993)}, y Overschee y De Moor (1994).

El algoritmo general de los métodos de subespacios consta de tres pasos principales: 1) el método N4SID basado en estrategias de ajuste de subespacios para la aproximación de la matriz de observabilidad ampliada Γ y/o de la secuencia de estado X; 2) descomposición en valores singulares de la matriz Γ para estimar el orden n del modelo de espacio de estados; 3) estimación de las matrices (A, B, C, D) resolviendo sistemas sobre determinados de ecuaciones lineales mediante técnicas de mínimos cuadrados o de mínimos cuadrados totales. En la Fig. 2 se muestra un diagrama del arreglo experimental realizado para la recolección de datos de salida/entrada en condiciones de funcionamiento de la unidad de OI objeto de estudio. Como variables de salidas del modelo matemático se consideraron el flujo F(t) y la conductividad C(t) del permeado y como variables de entrada la presión P(t) y el potencial hidrógeno pH(t) del agua de alimentación.

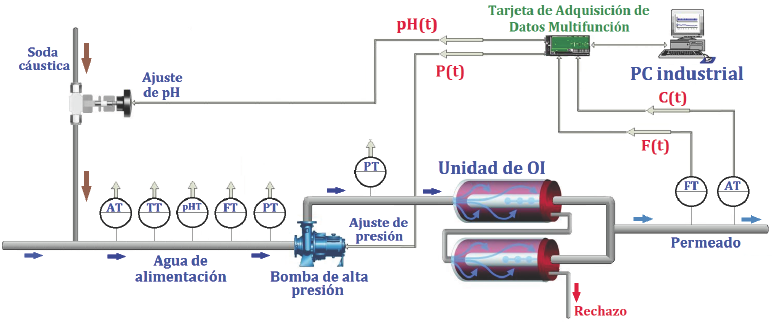
Fig. 2   Diagrama del arreglo experimental realizado para la recolección de datos de salida/entrada de la unidad de OI. 

Luego de aplicar el algoritmo general de identificacióndesistemasdinámicosbasadoenlos métodos de subespacios y procesar los resultados logrados (fuera de línea) se obtuvo el siguiente modelo matemático multivariable del comportamiento dinámico nominal de la planta objeto de estudio en el dominio de Laplace:

(6)

donde:

(7)

(8)

(9)

(10)

Se destaca, que la estructura del modelo matemático multivariable nominal Ec. (6) coincide con la propuesta por otros investigadores (ver por ejemplo, ^{Alatiqi y col., 1989}).

En la Fig.3 se exhiben los resultados de validación de las variables de salida (flujo y conductividad del permeado) del modelo matemático nominal obtenido de la unidad de OI objeto de estudio (Ec. 6), los cuales muestran un grado de adecuación (FIT) de 90.5 % y 89.5 % respectivamente. Por consiguiente, el modelo Ec. (6), describe de forma aceptada el comportamiento dinámico nominal de la planta objeto de estudio y por ende puede ser utilizado con fines de diseño de CPBM.

Fig. 3   Resultados de validación del modelo matemático obtenido. 

Los experimentos desarrollados en este trabajo posibilitaron establecer que durante el proceso de funcionamiento de la unidad de OI, como resultado del ensuciamiento paulatino e inevitable que tiene lugar en sus membranas, se originan variaciones (mayor del 10% de los valores del comportamiento dinámico nominal) en los parámetros dinámicos de las funciones de transferencias (Ecs. 7-10) del modelo nominal Ec. (6) de la planta. Por consiguiente, el diseño del controlador de este tipo de plantas debe dar solución a este complejo comportamiento dinámico.

3 Diseño de un controlador GPC multivariable para el control de las variables críticas de una unidad de OI

El GPC ha mostrado un buen desempeño con cierto grado de robustez, por lo cual ha sido utilizado en el control de una amplia gama de plantas industriales (ver por ejemplo: ^{Altinten, 2007}; ^{Romero y col., 2013}; ^{Zhang y col., 2013}; ^{Zidane y col., 2012}). Entre los éxitos del GPC se encuentra el propiciar una forma más general de formular el problema de control en el dominio del tiempo utilizando un modelo interno de la planta (modelo CARIMA), así como el control de forma directa de plantas multivariables, sin necesidad de utilizar desacopladores (^{Bao-cang, 2010}).

El modelo Ec. (6) de la unidad de OI objeto de estudio (planta) puede ser convertido (sin pérdida de precisión) en el siguiente modelo CARIMA multivariable con 2 entradas y 2 salidas (^{Isermann y Mu ̈nchhof 2011}), el cual se utiliza para predecir el comportamiento dinámico de las variables de salida de la planta:

(11)

donde, A(q ⁻¹⁾ y C(q ⁻¹⁾ son matrices polinomiales mónicas de dimensionesn x n, y B(q ⁻¹⁾ es una matriz polinomial de dimensión n x m, definidas como:

(12)

(13)

(14)

el operador ∆ se define como ∆ = 1−q ⁻¹, y(k) es el vector de salida de dimensión n×1, u(k) es el vector de control(entrada) de dimensión m×1,e(k) es el vector de ruido blanco de media cero de dimensión n×1, l es una matriz unitaria de dimensiones n × n, A_i, B_i y C_i representan a polinomios.

Considerando que los polinomios de ruido blanco coloreado son muy difíciles de estimar con suficiente exactitud (Camacho y Bordons, 1999), por simplicidad se supone que C(q ⁻¹⁾ = I. En este caso, el modelo (Ec. 11) se simplifica y se presenta en la forma:

(15)

La señal de control óptimo del GPC multivariable se obtiene mediante la minimización de la siguiente función objetivo cuadrática:

(16)

donde N ₁, N ₂ son los valores mínimo y máximo del horizonte de predicción, N_u es el horizonte de control, y^k+j es la predicción óptima j pasos hacia adelante de la salida de la planta, r(k + j) es la trayectoria de referencia futura, R y Q son matrices de peso (ponderación) definidas positivas de la señal de error y del esfuerzo en el control respectivamente, las cuales normalmente se eligen diagonales.

Para la obtención del predictor óptimo se utiliza la siguiente ecuación diofántica:

(17)

donde Ã(q ⁻¹⁾ = A(q ⁻¹⁾∆; E_j (q ⁻¹⁾ y F_j (q ⁻¹⁾ son matrices polinomiales únicas de dimensiones n × n y orden j−1 y n_α , respectivamente y se definen mediante las expresiones:

(18)

(19)

Multiplicando la Ec. (15) por ∆Ej(q^-1)q ^j se tiene:

(20)

En la Ec. (20) considerando la Ec. (17) y después de algunos arreglos se obtiene la siguiente ecuación de predicción óptima j pasos hacia adelante de la salida:

(21)

De la Ec. (21) se observa que todos los términos de ruido se encuentran en el futuro, lo cual significa que los mismos son desconocidos. Considerando el operador de esperanza matemática y teniendo en cuenta que E[e(k+ j)] = 0, el valor esperado de y(k+ j) se determina como:

(22)

Creando la matriz polinomial:

(23)

donde el grado de G_j (q ⁻¹⁾ < j, y sustituyendo la Ec. (23) en la Ec. (22) se obtiene:

(24)

En la Ec. (24), los dos últimos términos dependen de los valores pasados de las variables de salida y entrada de la planta y corresponden a la respuesta libre, mientras que el primer término depende sólo de los valores futuros de la señal de control y representa a la respuesta forzada. Por consiguiente, la Ec. (24) se presenta como:

(25)

donde,

(26)

El término de respuesta libre f_j se puede calcular de forma recursiva:

(27)

con f₀ = y(k) y (u(k + j) = 0 para j ( 0.

La predicción (Ec. 25) se representa en forma matricial mediante la expresión:

(28)

donde, G representa a la matriz de respuesta forzada y f a la respuesta libre,

(29)

(30)

(31)

La minimización de la función objetivo Ec. (16) se realiza de forma analítica:

(32)

Si no existen restricciones, la ley de control óptima se obtiene mediante la expresión:

(33)

Debido a la estrategia de horizonte móvil, en el instante t solamente se necesita la primera acción ∆u(t) del vector de control u (Ec. 30). Por consiguiente, solo la primera fila de la matriz ( _^GTRG +Q)^{−1 _{GT R}} , es decir K, resulta necesario calcular. Consecuentemente, la ley de control se obtiene como:

(34)

Por ende, la ley de control representa a una matriz de ganancia lineal que multiplica al error de predicción entre la trayectoria de referencia futura y la predicción de la respuesta libre de la planta. De (34) se obtiene el vector de señales actuales de control que ingresa a los actuadores de la planta (motor de la bomba de alta presión y válvula de ajuste de pH) en cada periodo de muestreo, el cual se representa en la forma:

(35)

Considerando que durante el proceso de purificación del agua de alimentación ocurre un ensuciamiento paulatino e inevitable de las membranas de la unidad de OI, lo que conlleva a que se originen variaciones en los parámetros dinámicos de dicha planta, el GPC diseñado se distingue por presentar un módulo de identificación y reajuste de parámetros en línea, el cual inicialmente convierte el modelo matemático multivariable nominal (Ec. (6)) en un modelo CARIMA multivariable (Ec. 15) con 2 entradas y 2 salidas, luego de forma recursiva calcula en cada periodo de muestreo los parámetros actuales (θ(k)) de las matrices polinomiales A(q ⁻¹ ) y B(q ⁻¹ ), y finalmente reajusta dichos parámetros en el modelo de predicción (Ec. 15), así como en el algoritmo de obtención de la señal de control u. De esta forma, se garantiza que los parámetros del modelo de predicción y del algoritmo de control sean adecuados a las variaciones de la dinámica de la planta y por consiguiente se logra un aumento en la efectividad y precisión en el control. Es bien conocido, que la efectividad del GPC se encuentra directamente relacionada con la precisión del modelo de predicción (^{Clarke y col., 1987}). Es notorio destacar que los trabajos precedentes (ver por ejemplo: ^{Abbas, 2006}; ^{Ali y col., 2010}; ^{Bartman y col., 2009a}, 2009b; ^{Moncada-Valerio y col., 2012}; ^{Rivas-Perez y Sotomayor-Moriano, 2014}, etc.) no resuelven la problemática relacionada con la variación de los parámetros dinámicos de la unidad de OI como resultado del ensuciamiento paulatino e inevitable de las membranas.

En la Figura 4 se muestra el diagrama de bloques del sistema de control de la unidad de OI objeto de estudio con el GPC diseñado, donde w ₁(k), w ₂(k) representan a las referencias externas del flujo y de la conductividad del permeado, respectivamente.

Fig. 4   Diagrama de bloques del sistema de control de la unidad de OI con el controlador GPC multivariable diseñado. 

4 Resultados y discusión

Para la implementación del GPC diseñado se desarrolló un programa que se ejecuta en la PC industrial de la planta purificadora de agua potable (ver Fig. 1), basado en los siguientes pasos:

A continuación se presentan algunos resultados de simulación del sistema de control de la planta objeto de estudio considerando diferentes escenarios reales de operación industrial, con la finalidad de evaluar la efectividad del controlador GPC desarrollado. Los experimentos fueron diseñados en base a verificar la capacidad del GPC de seguimiento a las señales de referencia, así como de rechazo a perturbaciones externas en entornos cercanos a las condiciones de operación nominal de la planta objeto de estudio. Los parámetros de diseño del controlador GPC fueron los siguientes: periodo de muestreo T =15 s, horizonte de control N_u =3, horizonte de predicción N ₂ =10, R = diag(20, 2), Q = diag (0.5, 10).

Las especificaciones de las respuestas temporales consideradas del sistema de control fueron las siguientes: máxima velocidad de respuesta (tiempo de establecimiento (ts) mínimo) y máxima exactitud en el control (error de estado estacionario cero).

En la Fig. 5 se exhiben las respuestas temporales del sistema de control de la planta objeto de estudio con el controlador GPC diseñado frente: a) un escalón en la referencia del flujo de permeado de (0.3 a 1.0) m³/min; b) un escalón en la referencia de la conductividad del permeado de (6.0 a 1.2) μs/cm. De la figura se observa que el valor establecido de referencia del flujo de permeado (1.0 m³/min) se alcanza en un tiempo aproximado de 50 s, con 1.05 % de máximo sobreimpulso (M_p ), mientras que el valor establecido de referencia de la conductividad del permeado (1.2 μs/cm) se consigue en un tiempo aproximado de 70 s, con 1.10 % de máximo sobreimpulso. Estos resultados muestran que el controlador diseñado posibilita alcanzar los valores de referencias establecidos de las variables controladas de forma rápida y precisa.

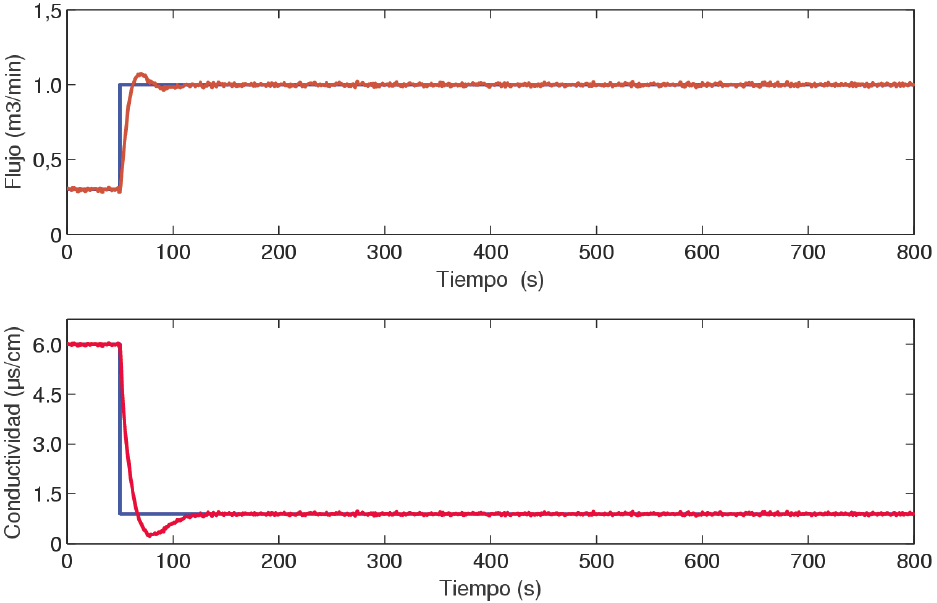
Fig. 5   Respuestas temporales del sistema de control de la planta objeto de estudio con el controlador GPC diseñado. 

En la Fig. 6 se muestran las respuestas temporales del sistema de control de la planta objeto de estudio con el controlador GPC diseñado frente al efecto de cambios abruptos de referencias que se originan en el instante de tiempo t = 300 s, así como de perturbaciones externas tipo escalón de magnitudes 0.3 m³/s y 1.5 μs/cm en el flujo y en la conductividad del permeado respectivamente, las cuales tienen lugar en el instante de tiempo t = 500 s. De la figura es posible observar que los nuevos valores de ambas referencias se alcanzan en un tiempo aproximado de 30 s (sin sobreimpulso), mientras que el efecto de ambas perturbaciones es rechazado en un tiempo aproximado (t_{s f} ) de 20 s. Estos resultados exhiben la capacidad satisfactoria del GPC diseñado de seguimiento de referencias variables, así como de rechazo de los efectos negativos de las perturbaciones externas.

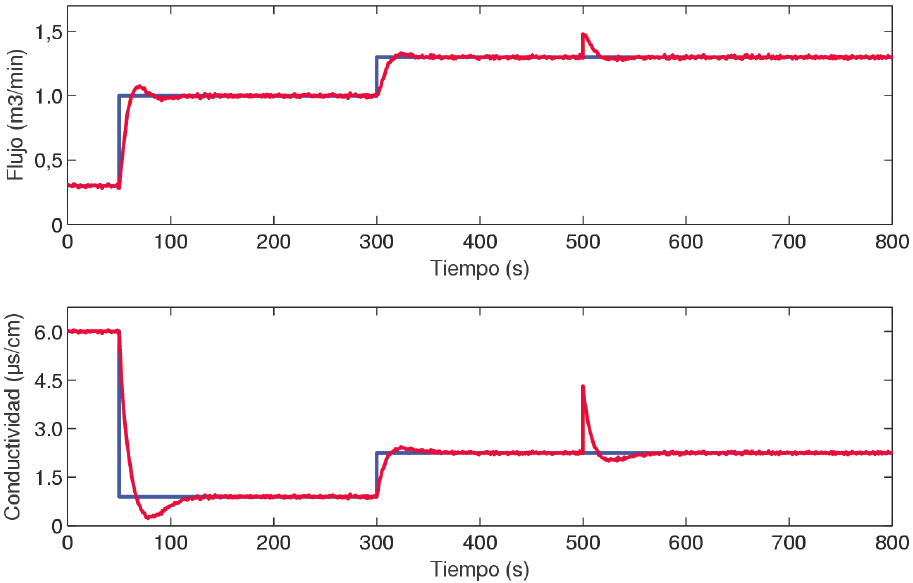
Fig. 6   Respuestas temporales del sistema de control de la planta objeto de estudio frente a cambios en las referencias y perturbaciones externas. 

Para evaluar la efectividad y ventajas comparativas del GPC desarrollado fueron diseñados otros controladores, entre los que se encuentran: un controlador de matriz dinámica (DMC) multivariable y dos controladores PI convencionales (para la planta desacoplada). El DMC multivariable se desarrolló en correspondencia con el procedimiento estándar de diseño (ver por ejemplo, Moncada y col. (2012)) con los siguientes parámetros: periodo de muestreo T =15 s, horizonte de control N_u =3, horizonte de predicción N ₂ =10, R = diag(30, 2), Q = diag(0.5, 10). Los controladores PI convencionales fueron diseñados en el dominio de la frecuencia considerando la estructura (Åström y Hägglund, 2009):

(36)

donde K_p, K_i son las ganancias proporcional e integral respectivamente, las cuales fueron deducidas en base a las siguientes especificaciones en el dominio de la frecuencia (^{Castillo-Garcia y col. 2013}): margen de fase Φ _m , frecuencia de cruce de ganancia ω _c y cero error de estado estacionario, en correspondencia con las expresiones de diseño (^{Feliu-Batlle y col., 2013}):

(37)

donde M_ii (jω _c ), i = 1,2 representan a M ₁₁(s) = F(s)/P(s) y M ₂₂(s) = C(s)/pH(s) del modelo nominal Ec. (6). Los parámetros obtenidos de los controladores PI fueron los siguientes: K_{P _F} = 31.6, K_{I _F} = 0.75 (para el lazo de control de flujo del permeado); K_{P_C} = 0.057, K_{I _C} = 0.0063 (para el lazo de control de conductividad del permeado).

Para cuantificar la efectividad de los controladores diseñados (análisis de robustez) se utilizaron los siguientesíndices de desempeño: la integral del error absoluto (IAE) y el esfuerzo (energía) de la señal de control (EU) (^{Feliu-Batlle y col., 2013}):

(38)

donde, t ₀ es el tiempo de comienzo del experimento y t_f es el tiempo en el que la respuesta del sistema entra en la banda del ± 2% de error con respecto al valor estacionario.

En la Fig. 7 se muestran los resultados comparativos de las respuestas temporales del sistema de control de la planta objeto de estudio con controladores GPC, DMC y PI desacoplados, considerando cambios abruptos en las referencias externas que se originan en el instante de tiempo t = 50 s, así como el efecto de perturbaciones externas tipo escalón (de magnitudes similares a las consideradas en el escenario anterior) que se producen en el instante de tiempo t=500s. De esta figura y de la ^Tabla1 es posible observar que el máximo sobre impulso (Mp) de las tres respuestas temporales es aproximadamente similar, pero el GPC posibilita alcanzar las referencias externas(t_s ), así como compensar el efecto negativo introducido por las perturbaciones externas (t_sf ) en un menor tiempo que los controladores DMC y PI. Los resultados comparativos de los índices de desempeño de los tres controladores se exhiben en la Tabla 1. De esta tabla es posible observar que el menor error absoluto y el menor esfuerzo (energía) en el control se obtienen con el GPC, por consiguiente este controlador es el que exhibe el mejor comportamiento robusto.

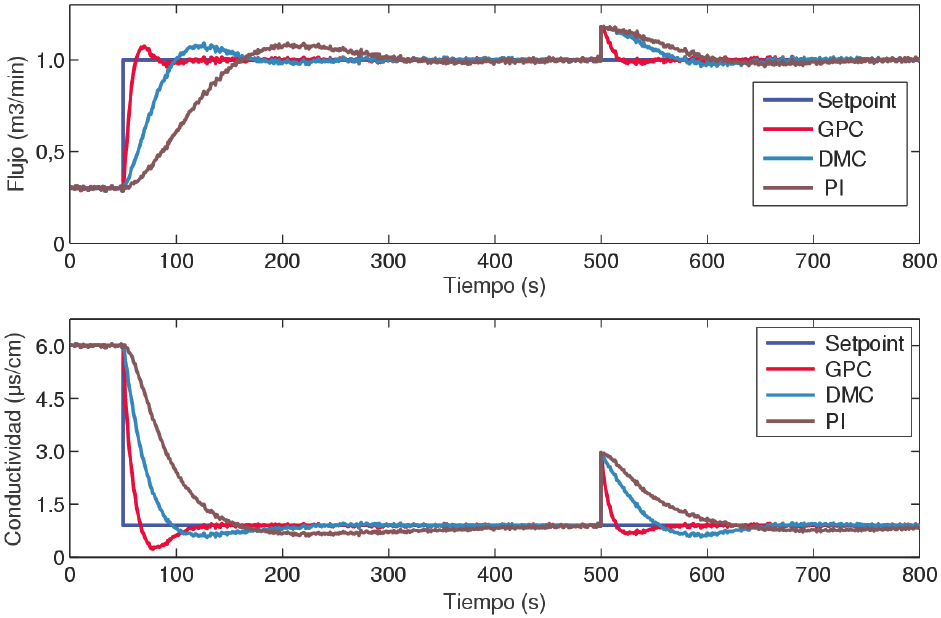
Fig. 7   Resultados comparativos de las respuestas temporales del sistema de control de la unidad de OI con GPC, DMC y PI desacoplados. 

Tabla 1  Resultados comparativos de los índices de desempeño del GPC, DMC y PI 

Estos resultados muestran que el controlador GPC diseñado permite obtener mejoras significativas en el control de la unidad de OI de la planta purificadora de agua potable objeto de estudio y por ende posibilita la producción de agua de uso farmacéutico de calidad consistente con un menor esfuerzo (energía) en el control.

Conclusiones

Se desarrolló el diseñó de un controlador predictivo generalizado (GPC) multivariable para el control efectivo de las variables críticas de una unidad de OI de una planta purificadora de agua potable de una industria farmacéutica, el cual se distingue por presentar un módulo de identificación y reajuste de parámetros en línea, el cual posibilita resolver la problemática relacionada con la variación de los parámetros dinámicos de la planta debido al ensuciamiento paulatino e inevitable de las membranas, y garantizar la obtención de agua de uso farmacéutico de calidad consistente.

Mediante la aplicación de los métodos de subespacios para la identificación de sistemas dinámicos se obtuvo un modelo matemático multivariable de la unidad de OI objeto de estudio. Los resultados de validación revelaron que el modelo matemático obtenido reproduce de forma adecuada el comportamiento dinámico de las variables críticas de la planta y por consiguiente, dicho modelo puede ser utilizado en el diseño del controlador GPC.

En base al modelo matemático obtenido de la unidad de OI se diseñó el controlador GPC y se desarrollóunprogramaparasuimplementaciónenuna PC industrial, el cual posibilita ejecutar el algoritmo de control en 7 pasos. Los resultados de simulación del sistema de control considerando diferentes escenarios reales de operación industrial de la planta objeto de estudio mostraron un buen desempeño del controlador GPC diseñado en correspondencia con los requerimientos de operación.

Los resultados comparativos de simulación del sistema de control con controladores GPC, DMC y PI mostraron que la mejor efectividad en el control de las variables críticas de la unidad de OI objeto de estudio se obtiene cuando se aplica el controlador GPC (ver Tabla 1), con lo cual se garantiza la obtención de agua de uso farmacéutico de calidad consistente con un menor esfuerzo en el control. Es importante destacar, que la aplicación del GPC multivariable en esta clase de plantas es muy conveniente, dado que permite operar a la unidad de OI en condiciones muy cercanas a las de operación óptima, situación imposible de lograr mediante controladores convencionales.

Los objetivos futuros de nuestras investigaciones incluyen finalizar la implementación del controlador GPC diseñado en la unidad de OI de la planta purificadora de agua potable objeto de estudio, así como intentar su generalización en otras plantas de la industria farmacéutica.