Volatility Contagion of Stock Returns of Microfinance Institutions in Emerging Markets: A DCC-M-GARCH Model

Ramírez-Silva, Roberto Alejandro; Cruz-Aké, Salvador; Venegas-Martínez, Francisco; Ramírez-Silva, Roberto Alejandro; Cruz-Aké, Salvador; Venegas-Martínez, Francisco

doi:10.21919/remef.v13i3.326

Servicios Personalizados

Revista

Articulo

Indicadores

Citado por SciELO
Accesos

Links relacionados

Similares en SciELO

Otros
Otros

Permalink

Revista mexicana de economía y finanzas

versión On-line ISSN 2448-6795versión impresa ISSN 1665-5346

Rev. mex. econ. finanz vol.13 no.3 Ciudad de México jul./sep. 2018

https://doi.org/10.21919/remef.v13i3.326

Articles

Volatility Contagion of Stock Returns of Microfinance Institutions in Emerging Markets: A DCC-M-GARCH Model

Contagio en la volatilidad de los rendimientos de las Instituciones Microfinancieras en los mercados emergentes: un modelo DCC-M-GARCH

Roberto Alejandro Ramírez-Silva¹^*

Salvador Cruz-Aké¹

Francisco Venegas-Martínez¹

^¹Instituto Politécnico Nacional, México

Abstract:

The objective of this paper is to analyze the contagion in the returns on the volatilities of the Microfinance Institutions (MFIs) that are listed in emerging stock markets in India, Indonesia, and Mexico. For this, local benchmarking variables and the global index-All Countries World Index (ACWI)-are included in the analysis. The methodology used is a Dynamic Conditional Correlation (DCC) multivariable GARCH model. The empirical findings show that contagion eﬀects only occur in periods of high volatility. One limitation of this research is that there are still few MFIs listed in stock markets, which does not allow for a broader study. The originality of this paper is the analysis of contagion in the returns of MFIs listed in stock markets. It is concluded that the performance of the analyzed MFIs is not aﬀected by external eﬀects of volatility, but rather for its fundamental results reflected in their level of liquidity in the stock market.

JEL Classification: C01; C32; G2

Keywords: Microfinance institutions; volatility of returns; GARCH and M-GARCH models; Dynamic Conditional Correlation (DCC)

Resumen:

El objetivo del presente trabajo es analizar el contagio en los rendimientos en las volatilidades de las Instituciones Microfinancieras (IMFs) que cotizan en mercados bursátiles emergentes en India, Indonesia y México. Para ello se incluyen en el análisis variables benchmarck locales y el índice global –All Countries World Index (ACWI). La metodología que se utiliza es la de un modelo multivariable GARCH de Correlación Condicional Dinámica (DCC). Los resultados empíricos encontrados muestran que los efectos de contagio sólo se dan en periodos de alta volatilidad. Una limitación que presenta esta investigación es que aún son pocas las IMFs listadas en bolsas, lo que impide realizar un estudio más amplio. La originalidad de este trabajo es el análisis de contagio en los rendimientos de las IMFs listadas en bolsa. Se concluye que el desempeño de las IMFs analizadas no se ve afectado por efectos externos de volatilidad, sino por sus resultados fundamentales reflejados en su nivel de liquidez bursátil.

Clasificación JEL: C01; C32; G2

Palabras claves: Instituciones microfinancieras; volatilidad de rendimientos; modelos GARCH and M-GARCH; Correlación Dinámica Condicional (DCC)

1. Introduction

An important resurgence of Microfinance Institutions (MFIs) took place in the 70’s when initially they were constituted as non-profit NGOs^¹, though the first antecedents are given since the 19th century in Europe (Germany).^² The MFIs mainly focus on providing financial services to the population that does not have access to conventional bank credit for lack of real collateral. MFIs face, continuously, two main objectives: 1) achieve financial sustainability, and 2) in-crease the number of clients. Currently, there are more than 2000 Microfinance Institutions (MFIs) in the world, with a total of 130 million clients and a Gross Loan Portfolio of 108 billion (USD)^³.

On the other hand, the number of MFIs that are listed on stock exchanges is still small worldwide. However, they account for 16.8 % of the total number of clients since they have a high degree of concentration -in their respective markets where they operate. It is worth mentioning that MFIs seek in the stock market resources more eﬃciently (quickly and at a lower cost). The main question that arises is: if this objective can be achieved without being aﬀected by the volatility from financial crises, which may discourage other MFIs from entering the stock market.

Due to the above concerns, ^{Wagner and Winker (2011)} and ^{Di Della (2011)} have studied the impact of financial crisis (for example, the sub-prime crisis, 2008) on the MFIs, particularly in periods of high volatility. However, the contagion in the volatility in the returns of the MFIs listed on stock markets has not yet been studied. In this sense, the goal of this paper is to analyze how volatility aﬀects them. This will allows us to better understand the eﬀects and consequences of high levels of volatility, which could be generated via global financial crises or high-volatility clusters. Thus, the main contribution of this research is to analyze, under a DCC-M-GARCH framework, how the contagion occurs in the volatilities of the returns of MFIs that are listed on stock exchanges in diﬀerent emerging economies.

This paper analyzes five MFIs from three emerging economies: India, Indonesia and Mexico.^⁴ Table 1 shows the studied MFIs and their characteristics such as number of clients, size of their portfolio and country of origin. In addition, for each MFI two reference variables are used in its corresponding stock market, and a global reference index -All Countries World index (ACWI). Table 2 describes each of the variables used (14 in total), it is shown the corresponding characteristics of: activity, currency in which they operate (in their respective stock market), and the period of analysis that comprises for each one of the MFIs, with daily frequency data.

Table 1 Microfinance Institutions (MFIs).

MFI	Reporting Period	GrossLoan Portfolio (USD million)	No. of Active Borrowers (thousands)	Country
Gentera	2015	1,317.76	2,861.72	Mexico
Financiera Independencia	2015	253.58	792.77	Mexico
Bharat Financial Inclusion	2014	671.79	5,325.24	India
Limited: NSE and BSE
Bank Rakyat Indonesia	2012	10,897.40	12,918.43	Indonesia

Source: Own elaboration

Table 2 Description of Variables.

Variables	Definition	Activity	Country	Currency	Starting date	Ending date
Gentera	Gentera	IMF	Mexico	MXN	03-01-11	29-01-16
IPC	Price Index and Quotations	Stock index	Mexico	MXN	03-01-11	29-01-16
MF	Mexican Found	Investment	EEUU	USD	03-01-11	29-01-16
ACWI	All Country World Index	Index	World	USD	10-07-12	29-01-16
FI	Financiera Independencia	IMF	México	MXN	03-01-11	29-01-16
BFIL_NSE	Bharat Financial Inclusion Limited NSE	IMF	India	INR	03-01-11	29-01-16
N50	Nifty 50	Stock index	India	INR	03-01-11	29-01-16
iI50	ishares India 50	Stock index	India	INR	03-01-11	29-01-16
BFIL_BSE	Bharat Financial Inclusion Limited BSE	IMF	India	INR	03-01-11	29-01-16
BD&MFG	BOMBAY DYEING & MFG.CO LTD	Textil	India	INR	03-01-11	29-01-16
BRFL	Bombay Rayon Fashion Limited	Textil	India	INR	03-01-11	29-01-16
BRI	Bank Rakyat Indonesia	Bank	Indonesia	IDR	04-03-13	29-01-16
JII	Jakarta Islamic Index	Stock index	Indonesia	IDR	04-03-13	29-01-16
TLK	TLK PT Telekomunikasi Indonesia	Comunications	Indonesia	IDR	04-03-13	29-01-16

Source: the data was obtained from Yahoo Finance.

It is important to point out that the period of analysis is not the same for all MFIs. The reason is that, on the one hand, this research seeks to obtain as many observations as possible with the aim of achieving more robust results and, on the other hand, it is understandable that the periods are not homogeneous since the MFIs began to operate in the stock market on diﬀerent dates; see the last two columns of Table 2.

In what follows, a descriptive statistical analysis is carried out in Table 3, According to the fifth column, all the returns are leptokurtic. Moreover, none of the returns are normally distributed according to the Jarque-Bera test. In Table 4, the unit root test was performed on each variable, using the Dickey Fuller Augmented test, under the three specifications: intercept, trend and intercept, and none. The results show that there is no empirical evidence of an explosive behavior in the analyzed variables.

Table 3 Descriptive statistics (in the returns of the variables).

Returns	Mean	Std. Dev.	Skewness	Kurtosis	J-B
Gentera	0.0004	0.02	0.2	7.0	850.1
IPC	0.0001	0.01	-0.2	5.7	382.8
MF	-0.0003	0.01	-0.3	5.2	282.0
ACWI	0.0002	0.01	-0.5	5.8	337.0
FI	-0.0008	0.02	0.3	9.7	2395.5*
BFIL_NSEN50	0.0005	0.04	0.4	6.8	786.2
N50	0.0002	0.01	-0.1	4.5	116.1
iI50	0.0001	0.01	-0.5	6.1	568.8
BFIL_BSE	0.0005	0.04	0.5	7.0	942.7
BD&MFG	-0.0007	0.04	-7.9	181.6*	1755490.3*
BRFL	0.0001	0.02	0.5	16.5	10043.1*
BRI	0.0006	0.02	0.3	5.7	211.5
JII	0.0000	0.01	0.1	6.2	289.5
TLK	0.0003	0.02	-0.1	5.9	240.2

Some results obtained, marked with the symbol “ * “ may seem to be erroneous; however, its result is due to values of high percentage variation of some observations, within the period of analysis.

Source: own elaboration with data from Yahoo Finance. The results were obtained using software EViews 7

Table 4 Results from Augmented Dickey-Fuller test (in the returns of the variables).

	Intercept		Trend and Intercept		None
Variable	t-Statistic*	Prob.	t-Statistic**	Prob.	t-Statistic***	Prob.
Gentera	-35.48	0.000	-35.51	0.000	-35.48	0.000
IPC	-34.13	0.000	-34.12	0.000	-34.14	0.000
MF	-21.67	0.000	-21.70	0.000	-21.66	0.000
ACWI	-25.02	0.000	-25.12	0.000	-25.00	0.000
FI	-35.17	0.000	-35.17	0.000	-35.13	0.000
BFIL_NSE	-29.03	0.000	-29.13	0.000	-29.04	0.000
N50	-33.10	0.000	-33.10	0.000	-33.10	0.000
iI50	-31.48	0.000	-31.51	0.000	-31.49	0.000
BFIL_BSE	-29.94	0.000	-30.03	0.000	-29.95	0.000
BD&MFG	-34.07	0.000	-34.06	0.000	-34.07	0.000
BRFL	-29.22	0.000	-29.20	0.000	-29.23	0.000
BRI	-23.77	0.000	-23.75	0.000	-23.77	0.000
JII	-18.50	0.000	-18.49	0.000	-18.52	0.000
TLK	-25.47	0.000	-25.46	0.000	-25.48	0.000

Source: own elaboration with data from Yahoo Finance. The results were obtained by using software EViews 7.

In order to detect whether there are long-term memory eﬀects in the returns of each variable, Hurst exponent is calculated. The latter is a useful indicator to examine whether returns have long-term memory -a characteristic useful to forecast future values. It is worth mentioning that Hurst’s exponent can be equal to 0.5 (without long-term memory), greater than 0.5 (long-term memory), and less than 0.5 (mean reversion). It is also important to notice that long-term memory violates the Eﬃcient Market Hypothesis (EMH), established by ^{Fama (1970)}. Moreover, this research computes an index of stock market liquidity^⁵ in order to find some relationship between the eﬀects of long memory and low stock market liquidity.

The obtained results, in relation to the Hurst exponent, show that Gentera and BRI do not present strong empirical evidence of long-term memory in their returns with Hurst exponents of 0.519 and 0.493, respectively.^⁶ These results can be seen in the fourth column (in descending order) of Table 5. With respect to the obtained results in the liquidity index, see the sixth column (in ascending order) of Table 5, the MFIs that appear with less liquidity are FI and BRI with an index of 81.6 and 90.9, respectively.

Based on the previous results, there is not a pattern in the behavior between long-term memory and low market liquidity (as would be expected at first). However, we can highlight the case of FI with long memory and low liquidity, 0.56, 81.6 %, respectively. In contrast, Gentera shows an acceptable liquidity of 98 % and a Hurst exponent of 0.519. Notice also that BFIL_NSE and BFIL_BSE provide empirical evidence of long memory in its returns but with high levels of stock market liquidity -see columns fifth and seventh of Table 5.

Table 5 Hurst exponent and liquidity index (li).

Variable returns	Hurst/Exp.	Liquidity* index (li)	Variable returns	Hurst/Exp. Ranked	Variable returns	(li) renked
Gentera*	0.519	98%	BFIL_NSE*	0.586	FI*	81.60%
IPC	0.505	100%	BFIL_NSE*	0.586	BRI*	90.90%
MF	0.561	97.50%	MF	0.561	BRFL	97.40%
ACWI	0.54	100%	FI*	0.56	MF	97.50%
FI*	0.56	81.60%	N50	0.549	Gentera*	98%
BFIL_NSE*	0.586	99.30%	iI50	0.545	TLK	99.25%
N50	0.549	99.40%	ACWI	0.54	BFIL_NSE*	99.30%
iI50	0.545	100%	BD&MFG	0.534	N50	99.40%
BFIL_BSE*	0.586	99.50%	Gentera*	0.519	BD&MFG	99.40%
BD&MFG	0.534	99.40%	BRFL	0.519	JII	99.40%
BRFL	0.519	97.40%	IPC	0.505	BFIL_BSE*	99.50%
BRI*	0.493	90.90%	TLK	0.495	IPC	100%
JII	0.474	99.40%	BRI*	0.493	ACWI	100%
TLK	0.495	99.25%	JII	0.474	Ii50	100%

Source: own elaboration. The results were obtained with the use of the R software, using the "pracma"library.

Each IMF is identified with the symbol “*”.

It is important to point out that not all the MFIs analyzed have had an acceptable long-term performance (in the period of analysis) in their accumulated returns. Only Gentera and BRI had a better performance than the local reference index in their respective markets, Mexico and Indonesia, respectively.

After the descriptive exploration of the variables, this research will be structured in the following way: section 2 provides a brief description of the M-GARCH model of Dynamic Conditional Correlation (DCC); section 3 presents the empirical findings for each specification of the MFIs (benchmark variables and a global index); finally, section 4 exposes the conclusion.

2. Dynamic Conditional Correlation (DCC)-M-GARCH

Recently, ^{Bala and Takimoto (2017)} analyze the eﬀects of the dynamic correlation, during periods of financial crisis, by using a DCC-M-GARCH econometric approach. These authors found that the dispersion of volatilities among deve-loped markets is greater than in emerging markets. Previously, ^{Mollah et al. (2014)} study 63 countries during the period of the global financial crisis. These authors find -through the use of DCC- that contagion of volatility occurs in 46 out of 63 countries that is, in 73 % of the analyzed countries. Although the previous studies allow us to see some results related to the DCC-M-GARCH methodology in assessing the eﬀects of contagion within emerging and developed markets, there is no recent literature that focuses on volatility contagion of returns of the MFIs listed on the stock market.^⁷

On the other hand, ^{Visconti (2009)} argues that MFIs are aﬀected in diﬀe-rent ways, depending on the country in which they operate and the degree to which these countries are integrated into the global economy. In addition, the author points out that MFIs operating in developing countries are less aﬀected by financial crises due to close ties and constant monitoring of their clients. Moreover, ^{Krauss and Walter (2008)} applied a panel data approach (with fixed eﬀects) in order to examine whether MFIs are a good option to reduce the volatility of an investment portfolio since their clients are mostly micro-entrepreneurs. In this regard, it is important to consider that the main disadvantage that MFIs face is that their clients do not have real guarantees. However, they do have the advantage of being able to maintain a continuous monitoring of their clients, which allows having a better quality in the portfolio of microcredits granted.

2.1 Generalized Autoregressive Conditional Heteroscedastic model

In this subsection, we state the GARCH (p,q) model and highlight its main properties. The model is given by the following equation:

ht2=ω+Σi=1qαiεt-i2+Σj=1pβjht-j2 (1)

Where each ht2 is obtained in a recursive way by taking an initial value of the variance at time t = 0, with a backcast methodology:

h02=ϵ02=λTh^t=02+1-λΣj=0TλT-j-1ϵT-j2 (2)

In order to find the optimal vector θ ∈ (ω, α₁,…,α_q,β₁,…,β_p) of the parameters defined in equation (1), the most used algorithm of optimization is that from BHHH (^{Berndt, Hall, Hall and Hausman, Berndt et al.,1974}), which maximizes a likelihood function, as in equation (3).^⁸ The iterative optimization method from BHHH for each step is given by:

θi+1=θi+E∂2LT(i)∂θ∂θ'-1∂LTi∂θ (3)

Where the likelihood function to be maximized, assuming a normal distribution for the error term, satisfies:^⁹

Lt=-12log⁡2π-12log⁡ht2-12εt2ht2 (4)

On the other hand, by considering a system of n variables, we can express the error term as:

εtΦt-1~N0,DtRtDt (5)

εt=μtθ+ϵt. (6)

The error term vector is then modeled as follows:

εt=Ht12θzt. (7)

Here Ht12θ is a positive definite matrix of order n × n ; and represents the conditional variance of εt.

2.2 Dynamic Conditional Correlation

When studying volatility of diverse variables, the analysis is usually performed with a single equation of the GARCH family.^¹⁰ However, in order to explore how volatility jointly aﬀects the MFIs’ returns, we use a Dynamic Conditional Correlation (DCC) methodology that allows us to evaluate the impact on their performance (in terms of contagion). This research will now examine the relationship that exists between the conditional correlations and the conditional variances of the returns of the stock prices of the MFIs under study.^¹¹

In this work, we focus on the methodology proposed by ^{Engle (2002)}. Other authors as ^{Bauwens et al. (2003)}, ^{Wang and Tsay (2013)}, and ^{Ling and McAleer (2003)} propose other extensions of the multivariate-GARCH model with a system of non-related variables. Initially the BEKK model (a Multi-Variable GARCH model) was introduced under a bivariate representation by ^{Engle and Kroner (1995)}. Under this framework, a generalized multivariate ARCH model can be stated as follows:

Ht=C0'C0+Σk=1KΣi=1qAik'εt-iεt-i'Aik+Σk=1KΣi=1qGik'Ht-iGik (8)

Recently, ^{Bauwens et al. (2012)} have replaced the BEKK model by other specifications, a DCC model. In this case, it is possible to specify the model (in two steps) in order to obtain a covariance matrix. In this regard, two main dynamic coeﬃcients of correlation were discussed by ^{Engle (2002)}. On one hand, one of them is the rolling correlation estimator for returns with mean zero, which is defined by:

ρ^12,t=Σs=t-n-1t-1r1,sr2,sΣs=t-n-1t-1r1,s2Σs=t-n-1t-1r2,s2 (9)

On the other hand, the coeﬃcient of correlation of exponential smoothing is defined as:

ρ^12,t=Σs=1t-1λt-j-1r1,sr2,sΣs=1t-1λt-j-1r1,s2Σs=1t-1λt-j-1r2,s2 (10)

The DCC is defined from the covariance matrix H_t, as follows:^¹²

Ht=Eϵtϵt'|It-1 (11)

The matrix H_t can be decomposed, from the following expression:

Ht=DtRtDt (12)

Dt=diag hiit1/2⋯hNNt1/2 (13)

In this way, it is possible to obtain the dynamic conditional correlation(R_t) from expression (12). The M-variable likelihood maximization can be applied in two steps by GMM optimization (Newey and MacFaden, 1994) according to the optimization methodology proposed by ^{Engle (2002)}; assuming normally distributed errors as in equations (15) and (16). Hence, the two-step optimization method expressed in aggregated form is:

Lθ,ϕ=LVθ+LCθ,ϕ (14)

The first step considers the following objective function:

LVθ=-12Σtnlog2π+logDt2+rt'Dt-2rt (15)

In the second step, we have

LCθ,ϕ=-12ΣtlogRt+ϵt'Rt-1ϵt-ϵt'ϵt (16)

3.Empirical result

3.1 MFIs systems

We present now the results obtained with a system of non-related variables for each MFI (with benchmark variables) for every stock market analyzed. The selection of the GARCH model and the error specification, to obtain the DCCs in each market, are chosen according to the less explosive parameters, see Table 6. The estimations are shown in Table 7. Subsequently, we present the DCCs for each MFIs and their benchmark variables, see Figures 4 and 5. Finally, in Table 7 we calculate the arithmetic and geometric maens for each estimated DCC considering the period of analysis.

Table 6 Model GARCH family (specifications).

MFIs Systems Not considering ACWI	GARCH Model	Error Specification
Gentera, IPC, MF	GARCH (1,1)	t-student
FI, IPC, ;MF	GARCH (1,1)	t-student
BFIL_ NSE, N50, iI50	GJR-GARCH (1,1)	t-student
BFIL_BSE, BD&MFG, BRFL	GJR-GARCH (1,1)	GED
BRI, JII, TLK	GARCH (1,1)	Normal
Gentera, IPC, ACWI	GARCH (1,1)	Normal
FI; IPC, ACWI	EGARCH (1,1)	GED
BFIL_NSE, N50, ACWI	GARCH (1,1)	t-student
BFIL_BSE, BD&MFG, ACWI	GARCH (1,1)	t-student
BRI, JII ACWI	EGARCH (1,1)	t-student

Note: criteria selection is according to the less explosive parameters.

The results were obtained by using the R software, "fGARCH"library.

Table 7 Econometric results (MFIs and Benchmarks).

	Coef. (1) Std. Err.		Coef. (2) Std. Err.		Coef. (3) Std. Err.		Coef. (4) Std. Err.		Coef. (5) Std. Err.
Gentera_ω	0.000009	FI_ω	0.000083	BFIL_NSE_ω	0.000241	BFIL_BSE_ω	0.000225	BRI_ω	0.000011
Gentera_ω	(0.000014)	FI_ω	(0.000051)	BFIL_NSE_ω	(0.000121)*	BFIL_BSE_ω	(0.00005)*	BRI_ω	(0.000009)
Gentera_α	0.08659	FI_α	0.348359	BFIL_NSE_α	0.158495	BFIL_BSE_α	0.130941	BRI_α	0.055043
Gentera_α	(0.037231)*	FI_α	(0.12433)*	BFIL_NSE_α	(0.049523)*	BFIL_BSE_α	(0.030491)*	BRI_α	(0.027312)*
Gentera_β	0.89872	FI_β	0.650641	BFIL_NSE_β	0.618593	BFIL_BSE_β	0.629758	BRI_β	0.926208
Gentera_β	(0.027132)*	FI_β	(0.136032)*	BFIL_NSE_β	(0.136525)*	BFIL_BSE_β	(0.056455)*	BRI_β	(0.016712)*
IPC_ω	0.000001	IPC_ω	0.000001	N50_ω	0.000003	BD&MFG_ω	0.000037	JII_ω	0.000006
IPC_ω	(0.000002)	IPC_ω	(0.000003)	N50_ω	(0.000005)	BD&MFG_ω	(0.000004)*	JII_ω	(0.00001)
IPC_α	0.065897	IPC_α	0.066201	N50_α	0.000003	BD&MFG_α	0.02046	JII_α	0.09792
IPC_α	(0.02605)*	IPC_α	(0.029512)*	N50_α	(0.026756)	BD&MFG_α	(0.000026)*	JII_α	(0.024537)*
IPC_β	0.922272	IPC_β	0.921662	N50_β	0.928628	BD&MFG_β	0.951826	JII_β	0.873711
IPC_β	(0.029107)*	IPC_β	(0.032855)*	N50_β	(0.01574)*	BD&MFG_β	(0.009623)*	JII_β	(0.053657)*
MF_ω	0.000005	MF_ω	0.000005	iI50_ω	0.000021	BRFL_ω	0.000016	TLK_ω	0.000007
MF_ω	(0.000006)	MF_ω	(0.000006)	iI50_ω	(0.000009)*	BRFL_ω	(0.000023)	TLK_ω	(0.000003)*
MF_α	0.115317	MF_α	0.115912	iI50_α	0.036828	BRFL_α	0.178185	TLK_α	0.044075
MF_α	(0.028479)*	MF_α	(0.027632)*	iI50_α	(0.020836)*	BRFL_α	(0.091392)**	TLK_α	(0.009175)*
MF_β	0.871226	MF_β	0.870042	iI50_β	0.822952	BRFL_β	0.756588	TLK_β	0.937472
MF_β	(0.039183)*	MF_β	(0.03935)*	iI50_β	(0.054078)*	BRFL_β	(0.165688)*	TLK_β	(0.013027)*
DCC_I	0.022961	DCC_I	0.02871	DCC_I	0.012854	DCC_I	0.018947	DCC_I	0.006419
DCC_I	(0.009062)*	DCC_I	(0.009961)*	DCC_I	(0.00433)*	DCC_I	(0.011151)**	DCC_I	(0.005797)
DCC_II	0.928073	DCC_II	0.937239	DCC_II	0.97705	DCC_II	0.914855	DCC_II	0.952879
DCC_II	(01.031519)*	DCC_II	(0.02274)*	DCC_II	(0.007167)*	DCC_II	(0.02149)*	DCC_II	(0.028827)v

Parameters are significant at: 5 % p-value (*) and 10 % p-value (**), respectively.

Source: own elaboration. The results were obtained with the use of the R software, using the libraries: “rugarch” and “rmgarch”.

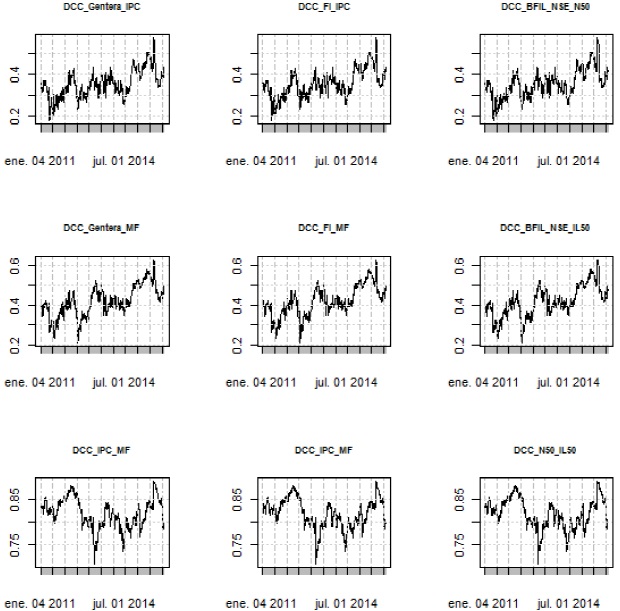
Source: own elaboration with the use of the R software.

Figure 1 Dynamic Conditional Correlations (MFIs: Gentera, FI, and BFIL_N SE).

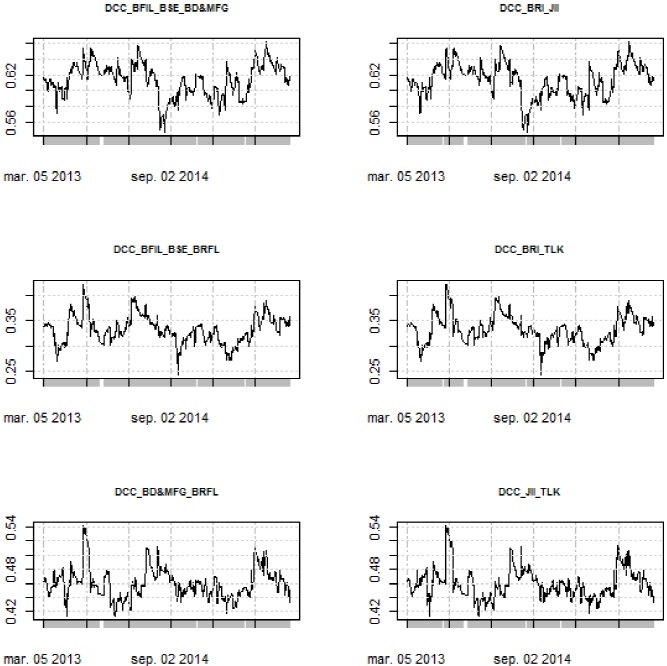
Source: own elaboration with the use of the R software.

Figure 2 Dynamic Conditional Correlations (MFIs: BF IL_BSE, BRI)

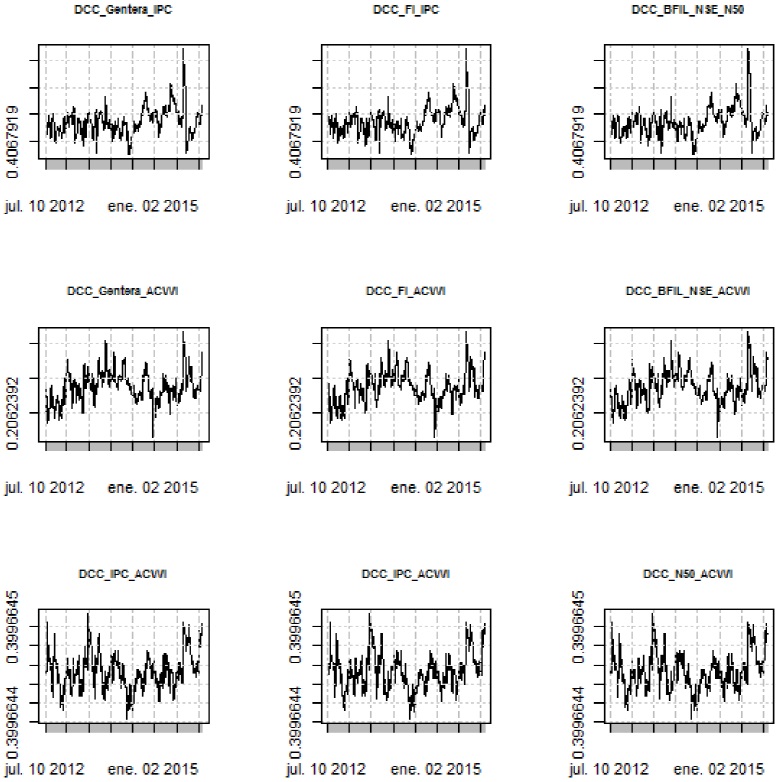
Source: own elaboration with the use of the R software.

Figure 3 Dynamic Conditional Correlations with ACWI (MFIs: Gentera, FI, and BFIL_N SE).

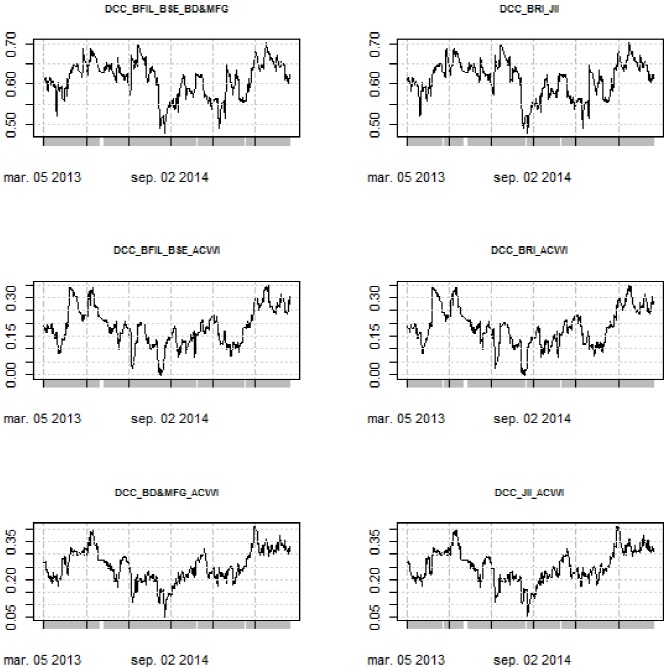
Source: own elaboration with the use of the R software.

Figure 4 Dynamic Conditional Correlations with ACWI (MFIs: BFIL_BSE; BRI).

Table 7 shows the estimated coeﬃcients for each MFI and its benchmark variables (based on the criteria in Table 6). The obtained results show that the specification in each equation successfully captures the estimated variances with persistence in both series εit-12 and hit-12 respectively. However, in the case of the parameters ωi, some specifications of the GARCH models capture that persistence in a smaller proportion; see columns (1)-(5) in Table 6. It can also be observed (in the same table) that for the estimated ωi in the columns (1) and (2) it is not possible to obtain a long-term variance.

It can be also observed in Figures 1 and 2 that it is not possible to appreciate a pattern (or contagion) common in the DCCs in each system of the MFIs. In other words, the particular specifications for each model of the GARCH family, according to the criteria in Table 5, do not capture a common contagion in the volatilities for each MFI. Contagion in volatilities can only be seen in some peaks with high volatility clusters, but not within the entire analysis period. Furthermore, we can see, in Table 8, that the arithmetic and geometric means do not show common patterns in the behavior of the DCCs in the analyzed stock markets.

Table 8 Means of Dynamic Conditional Correlations (DCCs).

Arithmetic Mean		Arithmetic Mean		Arithmetic Mean		Arithmetic Mean		Arithmetic Mean
DCC_Gentera_IPC	0.43	DDC_FI_IPC	0.14	DCC_BFIL_NSE_N50	0.36	DCC_BFIL_BSE_BD&MFG	0.28	DCC_BRI_JII	0.61
DCC_Gentera_MF	0.12	DCC_FI_MF	0.09	DCC_BFIL_NSE_iI50	0.41	DCC_BFIL_BSE_BRFL	0.12	DCC_BRI_TLK	0.35
DCC_IPC_MF	0.22	DCC_IPC_MF	0.22	DCC_N50_iI50	0.82	DCC_BD&MFG_BRFL	0.13	DCC_JII_TLK	0.47
Geometric Mean		Geometric Mean		Geometric Mean		Geometric Mean		Geometric Mean
DCC_Gentera_IPC	0.43	DCC_FI_IPC	0.15	DCC_BFIL_NSE_N50	0.35	DCC_BFIL_BSE_BD&MFG	0.27	DCC_BRI_JII	0.61
DCC_Gentera_MF	0.11	DCC_FI_MF	0.12	DCC_BFIL_NSE_iL50	0.41	DCC_BFIL_BSE_BRFL	0.12	DCC_BRI_TLK	0.35
DCC_IPC_MF	0.21	DCC_IPC_MF	0.20	DCC_N50_iI50	0.82	DCC_BD&MFG_BRFL	0.12	DCC_JII_TLK	0.47

Source: own elaboration with the use of the R software.

3.2 MFIs systems considering ACWI

In order to analyze the contagion (emphasizing in the analysis of external sources of contagion) in the volatilities of the returns of the MFIs that are listed in the stock market, we use a global reference index, particularly the All Country World Index (ACWI). The latter captures the sources of capital return for 23 emerging markets and 23 developed markets. In the same order of ideas, we can observe, in Table 8, the results obtained with respect to hit2 for each equation. These results show that the series εit-12 and hit-12 acceptably capture persistence in volatilities. However, for the case of the !_i parameters in some of the estimated GARCH family models, especially model (3) of Table 8, the results suggest that it is not possible to obtain a long-term variance. It is important to notice that in the estimated models, in columns (1), (2), (4) and (5) of Table 9, the long-term variances can be partially obtained.

Table 9 Econometric results including ACWI (MFIs and Benchmarks).

	Coef. -1 Std. Err.		Coef. -2 Std. Err.		Coef. -3 Std. Err.		Coef. -4 Std. Err.		Coef. -5 Std. Err.
Gentera_ω	0.000009	FI_ω	0.018425	BFIL_NSE_ω	0	BFL_BSE_ω	0	BRI_ω	-0.034736
Gentera_ω	-0.000016	FI_ω	-0.01558	BFIL_NSE_ω	-0.000001	BFL_BSE_ω	-0.000001	BRI_ω	(0.000002)*
Gentera_α	0.102476	FI_α	0.415963	BFIL_NSE_α	0.002846	BFL_BSE_α	0.005318	BRI_α	-0.133189
Gentera_α	(0.050604)*	FI_α	(0.241269)**	BFIL_NSE_α	(0.000271)*	BFL_BSE_α	(0.000493)*	BRI_α	(0.000698)*
Gentera_β	0.883797	FI_β	0.959156	BFIL_NSE_β	0.996154	BFL_BSE_β	0.993681	BRI_β	0.995635
Gentera_β	(0.024269)*	FI_β	(0.022523)*	BFIL_NSE_β	(0.000192)*	BFL_BSE_β	(0.000162)*	BRI_β	(0.002131)*
IPC_ω	0.000001	IPC_ω	-0.234286	N50_ω	0.000002	ED&MFG_ω	0.000838	JII_ω	-0.132074
IPC_ω	-0.000004	IPC_ω	(0.004241)*	N50_ω	-0.000002v	ED&MFG_ω	(0.000138)*	JII_ω	(0.005575)*
IPC_α	0.064805	IPC_α	-0.128804	N50_α	0.047321	ED&MFG_α	0.151094	JII_α	-0.114812
IPC_α	-0.061065	IPC_α	(0.015623)*	N50_α	(0.018641)*	ED&MFG_α	(0.073693)*	JII_α	(0.019883)*
IPC_β	0.921114	IPC_β	0.975735	N50_β	0.929635	ED&MFG_β	0	JII_β	0.984505
IPC_β	(0.065666)*	IPC_β	(0.000055)*	N50_β	(0.022908)*	ED&MFG_β	-0.0152	JII_β	(0.000004)*
ACWI_ω	0.000004	ACWI_ω	-0.509387	ACWI_ω	0.000004	ACWI_ω	0.000003	ACWI_ω	-0.406118
ACWI_ω	(0.000001)*	ACWI_ω	(0.008383)*	ACWI_ω	-0.000003	ACWI_ω	-0.000009	ACWI_ω	(0.008839)*
ACWI_α	0.142967	ACWI_α	-0.183733	ACWI_α	0.131929	ACWI_α	0.124324	ACWI_α	-0.184375
ACWI_α	-0.023802	ACWI_α	(0.022734)*	ACWI_α	(0.028282)*	ACWI_α	(0.054511)*	ACWI_α	(0.01155)*
ACWI_β	0.79178	ACWI_β	0.94509	ACWI_β	0.80366	ACWI_β	0.820754	ACWI_β	0.959311
ACWI_β	(0.032163)*	ACWI_β	(0.000083)*	ACWI_β	(0.0426)*	ACWI_β	(0.088538)*	ACWI_β	(0.000129)*
DCC_I	0.030803	DCC_I	0.01329	DCC_I	0	DCC_I	0.019378	DCC_I	0.018014
DCC_I	(0.012936)*	DCC_I	(0.004497)*	DCC_I	-0.000071	DCC_I	(0.011497)*	DCC_I	(0.008203)*
DCC_II	0.884571	DCC_II	0.98671	DCC_II	0.91982	DCC_II	0.891205	DCC_II	0.924282
DCC_II	(0.060315)*	DCC_II	(0.00596)*	DCC_II	(0.246352)*	DCC_II	(0.037126)*	DCC_II	(0.087257)*

Parameters are significant at: 5 % p-value (*) and 10 % p-value (**), respectively.

Source: own elaboration. The results were obtained with the use of the R software, using the libraries: “rugarch” and “rmgarch”.

Finally, we can see in Figures 3 and 4, considering the global index (ACWI) as a point of reference, that it is not possible to observe a common pattern (in terms of contagion) in the DCC for each MFI system. It is worth mentioning that the previous results are similar to those obtained in the preceding section. In this way, the DCC obtained under the specification of the GARCH models do not capture a common contagion in the volatilities of the returns for each MFI. Basically, contagion in volatilities can only be seen in periods of high volatility. Complementing the previous results, it can be observed, in Table 9, that the arithmetic and geometric means do not have common patterns among the DCC of the studied markets.

Table 10 Dynamic Conditional Correlations (DCC).

Arithmetic Mean		Arithmetic Mean		Arithmetic Mean		Arithmetic Mean		Arithmetic Mean
DCC_Gentera_IPC	0.4	DCC_FI_IPC	0.1	DCC_BFIL_NSE_N50	0.42	DCC_BFIL_BSE_BD&MFG	0.29	DCC_BRI_JII	0.6
DCC_Gentera_ACWI	0.28	DCC_FI_ACWI	0.14	DCC_BFIIL_NSE_ACWI	0.21	DCC_BFIL_BSE_ACWI	0.19	DCC_BRI_ACWI	0.19
DCC_IPC_ACWI	0.62	DCC_IPC_ACWI	0.58	DCC_N50_ACWI	0.41	DCC_BD&MFG_ACWI	0.13	DCC_JII_ACWI	0.25
Geometric Mean		Geometric Mean		Geometric Mean		Geometric Mean		Geometric Mean
DCC_Gentera_IPC	0.39	DCC_FI_IPC	0.13	DCC_BFIL_NSE_N50	0.42	DCC_BFIL_BSE_BD&MFG	0.29	DCC_BRI_JII	0.6
DCC_Gentera_ACWI	0.27	DCC_FI_ACWI	0.14	DCC_BFIL_NSE_ACWI	0.21	DCC_BFIL_BSE_ACWI	0.19	DCC_BRI_ACWI	0.18
DCC_IPC_ACWI	0.62	DCC_IPC_ACWI	0.58	DCC_N50_ACWI	0.41	DCC_BD&MFG_ACWI	0.13	DCC_JII_ACWI	0.24

Source: own elaboration with the use of the R software.

4. Conclusions

This research has shown that there is not a pattern between long-term memory and liquidity in the studied MFIs. According to the analysis carried out on the DCC-M-GARCH approach, the eﬀects of contagion (in MFIs returns) only occur in periods of high volatility when considering local benchmark variables. Moreover, when considering the global index All Countries World Index (ACWI), the results confirm the empirical evidence.

As a recommendation arising from the empirical findings, the MFIs that obtain resources via the stock market should operate with eﬃcient methodologies in the selection of clients, which will impact in their level of liquidity in the stock market. It is also recommended for investors, both institutional and individual, consider MFIs in their investment portfolios in stability periods given that contagion only occurs in periods of high volatility.

References

Armendariz, B. and Marcuch, J. (2011). Economía de las microfinanzas. Fondo de Cultura Económica. México. [ Links ]

Bala D. A. and Takimoto, T. (2017). Stock Markets Volatility Spillover during Financial Crisis: A DCC-MGARCH with Skewed-t density Approach. Borsa Istanbul Review, 17(1), pp. 25-48. [ Links ]

Bauwens, L. Laurent, S., and Rombouts, J. V. K. (2003). Multivariate GARCH Models: A Survey. Journal of Applied Econometrics, 21(1), pp. 79-109. [ Links ]

Bauwens, L., Storti, G., and Violante, F. (2012). Dynamic Conditional Correlation Model Realized Covariance Matrices. Center for Operation Research and Econometrics, (2012/60), Discussion Paper. [ Links ]

Berndt, E. K., Hall, B. H., Hall, R. E., and Hausman, J. A. (1974). Estimation and Inference in Nonlinear Structural Models. Annals of Economic and Social Measurements, 3(4), pp. 653-665. [ Links ]

Bollerslev, T. (1986). Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics, 31(3), pp. 307-327. [ Links ]

Bollerslev, T. (1990). Modelling the Coherence in Short-run Nominal Exchange Rates: A Multivariate Generalized ARCH Model. Review of Economics and Statistics, 72(3), pp. 498-505. [ Links ]

Caporin, M. and McAleer, M. (2013). Ten Things You Should Know about the Dynamic Conditional Correlation Representation. Econometrics, 1(1), pp. 115-126. [ Links ]

Di Della, G. (2011). The impact of the Global Financial Crisis on Microfinance and Policy Implications. IMF Working Paper, 11/175. Washington DC. [ Links ]

Engle, R. F. (1982). Autoregressive Conditional Heteroskedasticity with Estimates of Variance of United Kingdom Inflation. Econometrica, 50(4), pp. 987-1008. [ Links ]

Engle, R. F. (2001), GARCH 101: The Use of ARCH/GARCH Models in Applied Econometrics. Journal of Econometric Perspective, 15(4), pp. 157-168. [ Links ]

Engle, R. F. (2002). Dynamic Conditional Correlation-A Simple Class of Multivariate Garch Models. Journal of Business and Economic Statistics, 20(3), pp. 339-350. [ Links ]

Engle, R. F. and Kroner, K. F. (1995). Multivariate Simultaneous Generalized ARCH. Econometric Theory, 11(1). Cambridge University Press. [ Links ]

Fama, E. F. (1970). Eﬃcient Capital Markets: A Review of Theory and Empirical Work. The Journal of Finance, 25(2), pp. 383-417. [ Links ]

Hurst, H. (1951). Long-term Storage Capacity of Reservoirs. Transactions of the American Society of Civil Engineers, 116(1), pp. 519-543. [ Links ]

Kelley, C. T. (1999). Iterative Methods of Optimization. Society for Industrial and Applied Mathematics. Philadelphia. [ Links ]

Krauss, Nicolas and Walter, Ingo. (2008). Can Microfinance Reduce Portfolio Volatility? Retrieved from: <https://www.microfinancegateway.org/sites/default/files/mfg-en-paper-can-microfinance-reduce-portfolio-volatility-dec-2008.pdf>. [ Links ]

Ling, S. and McAleer, M. (2003). Asymptotic Theory for a Vector ARMA-GARCH Model. Econometric Theory, 19(2), pp. 280-310. [ Links ]

Mollah, S., Zafirov, G. and Shahiduzzaman Quoreshi, A. M. M. (2014). Financial Market Contagion during the Global Financial Crisis. CITR Electronic Working Paper Series, paper No. 2014/5. Retrieved from: file:///C:/Documents%20and%20Settings/User/Mis%20documentos/Downloads/FM%20contagion%20during%20global%20crisis.pdf [ Links ]

Rodriguez Monrroy, Carlos and Huerga A. (2012). A Study of Four Listed Micro Finance Institutions. 6th International Conference on Industrial Engineering and Industrial Management. Retrieved from: http://oa.upm.es/19416/1/INVEMEM2012139806:pdf [ Links ]

Tusom Eren. (2015). “The Development of Microfinance Institutions in a Multi-Tier Frame-work”. Master Thesis in Banking and Finance. University of Zurich, Center for Microfiance. [ Links ]

Visconti Moro, R. (2009). Are Microfinance Institutions in Developing Countries a Safe Harbour against the Contagion of global Recession? International Finance Review, 10, pp. 389-438. Retrieved from: http://www.emeraldinsight.com/doi/abs/10.1108/S1569-3767%282009%290000010016 [ Links ]

Wagner, C. and Winker, A. (2011). The Vulnerability of Microfinance to Financial Turmoil-Evidence from the Global Financial Crisis. Development World 2011. [ Links ]

Wang, Y. and Tsay, R. S. (2013). On Diagnostic Checking of Vector ARMA-GARCH Models with Gaussian and Student-t Innovations. Econometrics, 1(1), pp. 1-3. [ Links ]

¹See ^{Armendariz and Maruch (2011)}.

²Credit cooperatives in Germany as Schulze-Delitzsch, Raiﬀeisen and Haas granted loans to low-income people who were not served by conventional banks in the 19th century. However, in the 1970s the roots are formed in the way modern microfinance currently operates (one of the main references is the Grameen Bank in Bangladesh), see ^{Tusom (2015)}.

³Source: Microfinance Information Exchange (MIX), data to 2015.

⁴For the particular case of Mexico, the MFI (Real Credit") was not considered, although it has a greater liquidity compared with "Microfinanciera Independencia", however, its availability of data does not extend until the beginning of the analysis period.

⁵This index shows the percentage of days with variation (in returns) within the analysis period.

⁶The MFIs have been marked with the "*"symbol for easy location.

⁷See also, ^{Rodríguez and Huerga (2012)}, these authors study MFIs that are listed on the stock exchange with a methodology focuses mainly on a descriptive approach.

⁸A more detailed description of other iterative methods of optimization can be found in ^{Kelley (1999)}.

⁹It is possible to assume a t-Student distribution or a Generalized Error Distribution (GED), see Nelson (1991).

¹⁰This kind of modeling was initially introduced by ^{Engle (1982)}, and lately it was generalized by ^{Bollerslev (1986)} and ^{Engle (2001)}.

¹¹See ^{Engle (2002)}.

¹²Right after the introduction of the DCC model by ^{Engle (2002)}, several drawbacks concerning with it were detected, in particular it does not have “moments”. Also, it does not maintain testable stability and regularity conditions, and the estimators in “two steps” are inconsistent. Finally, DCC has no asymptotic desirable properties (^{Caporin and McAleer, 2013}).

Received: January 06, 2017; Revised: October 03, 2017; Accepted: December 29, 2017

*Sección de Estudios de Posgrado e Investigación, Escuela Superior de Economía, Plan de Agua Prieta No. 66 Col. Plutarco Elías Calles, Unidad Profesional Adolfo López Mateos, Casco de Santo Tomás, Delegación Miguel Hidalgo, C.P. 11340. e-mail: alexramsilva@hotmail.com

This is an open-access article distributed under the terms of the Creative Commons Attribution License

Servicios Personalizados

Revista

Articulo

Indicadores

Links relacionados

Compartir

Revista mexicana de economía y finanzas

versión On-line ISSN 2448-6795versión impresa ISSN 1665-5346

Rev. mex. econ. finanz vol.13 no.3 Ciudad de México jul./sep. 2018

https://doi.org/10.21919/remef.v13i3.326