nueva página del texto (beta)
Inglés (pdf)
Artículo en XML
Referencias del artículo
Traducción automática
Enviar artículo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
1. Introduction
In the manufacturing field, the most economical production lot was originally presented by Taft (1918) with simple assumption of producing single product on single machine under the condition of perfection in production process. In real life situations, however, production of nonconforming/imperfect products is inevitable owing to diverse uncontrollable factors (Porteus, 1986; Boone, Ganeshan, Guo, & Ord, 2000; Kumar, Goyal, & Singhal, 2017; Muralidharan, Vallavaraj, Mahanti, & Patidar 2017; MohanDas, Ayyanar, Susaiyappan, Kalimuthu, 2017; Villarreal et al., 2018; Arun, Lincon, & Prabhakaran, 2019). Some nonconforming items can be reworked to restore their quality, and of course with extra cost (Inderfurth, Janiak, Kovalyov, & Werner, 2006; Makarova, Shubenkova, Mavrin, & Boyko, 2017; Zhang, Wu, & Tang, 2017; Chiu, Wu, Chiu, & Hwang, 2018). Further, various discontinuous multi-shipment policies are commonly used in distribution of end products in the real supply chain systems (Thomas, & Hackman, 2003; Nielsen, & Saha, 2018; Lin, Chen, Chiu, & Chiu, 2019).
To maximize utilization, producing multiproduct on a single machine using common cycle time discipline can be of assistance (He, Wu, & Zhang, 2018; Mehdizadeh, Gholami, & Naderi, 2018). Moreover, in the planning stage of fabrication, when multiproduct sharing a common component, the delayed differentiation strategy is constantly taken into consideration to cut short the cycle time and/or reduce total system cost (Swaminathan, & Tayur, 1998; Abbad, & Zahratahdi, 2008; Bernstein, DeCroix, & Wang, 2011; Chiu, Kuo, Chiu, & Chang, 2019). Motivated by the benefit of applying postponement strategy to the real vendor-buyer systems, Chiu, Kuo, Chiu and Chiu (2016) studied a multiproduct fabrication-shipment problem featuring postponement and product quality reassurances using mathematical modeling and differential calculus to decide the optimal operating decisions. They also demonstrated that various benefits (in terms of reduction of cycle length and system) can be gained from their research results.
Unlike the differential calculus methodology, a simplified algebraic method was presented by Grubbstrom and Erdem (1999) to resolve an economic order quantity model without reference to derivatives in their optimization procedure. Likewise, we present such a two-phase approach to the model explored by Chiu et al. (2016) and show that the optimal operating decisions to the problem can be found without using the derivatives.
2. Materials and methods
2. 1. The Proposed System
A two-stage multiproduct fabrication-shipment model is reexamined in this paper by the use of the mathematical modeling and a simplified algebraic method to find the optimal fabrication-distribution policy. Consider L distinct end products sharing a common intermediate component must be produced on a machine, and their separate annual demand λ i must be satisfied (where i =1, 2, …, L). Stage one (see Figure 1) manufactures common parts at a of P 1,0, and stage two fabricates in sequence L customized finished items at a rate P 1,i.
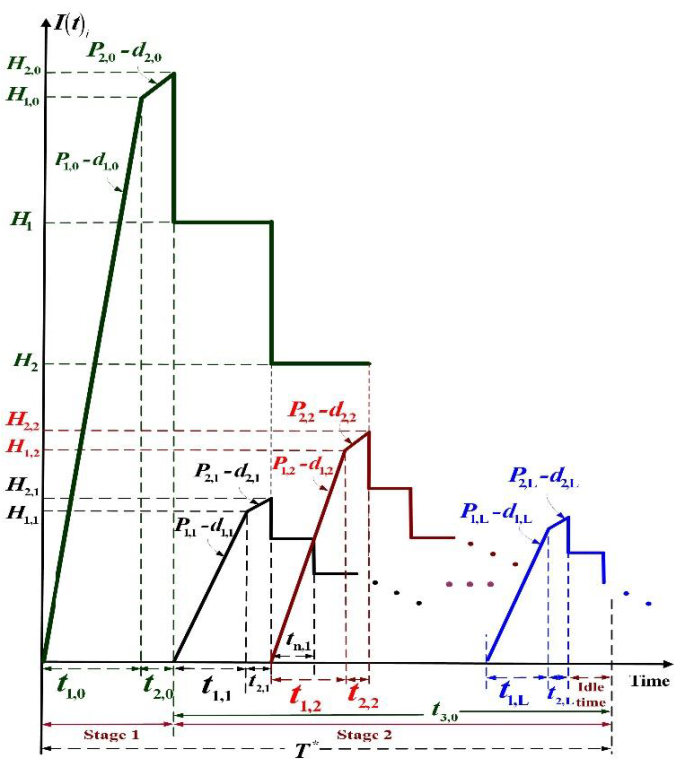
Figure 1 Inventory status of perfect quality common parts and end items in this study (Chiu et al., 2016).
In each stage, the manufacturing processes may generate x i portion of defects randomly, at a rate d 1,i ; so, (where d 1,i = x i P 1,i & i = 0, 1, 2, …, L; please note that i = 0 means the process is in stage 1 fabricating common parts). All stocks are inspected and a θ 1,i proportion of the defective items is identified as scrap (please note that 0 <= θ 1,i <= 1) and the other portion (1 - θ 1,i ) can be repaired via rework process in each cycle when of regular process ends, at a rate P 2,i (Figure 1).
Moreover, the rework is imperfect, a θ 2,i portion (0 <= θ 2,i <= 1) of reworked items are scrap (see Figure 2). Under no stock-out permitted assumption in this model, we must have (P 1,i - d 1,i - λ i ) > 0. The same notation used as in (Chiu et al., 2016) is listed in Appendix A.
Status of stocks at customer’s side is shown in Figure 3 and customer’s stock holding cost is (Chiu et al., 2016)
Applying the same mathematical modeling as in [1], total relevant system cost TC(T,n) includes the stage one, common part’s setup, variable fabrication, rework, disposal, and holding costs; and the stage two, L distinct end items’ sum of variable fabrication, setup, rework, disposal, and holding costs; and the fixed and variable distribution cost, and the buyers’ stock holding costs, as follows [1]:
Apply E[x] to cope with the randomness of x and with extra derivations, one finds E[TCU(T, n)] as follows (Chiu et al., 2016):
where
3. Results and discussions
3. 1. The proposed algebraic solution process
3. 1. 1. Phase 1: deciding n*
By observing E[TCU(T, n)] (i.e., Eq. (3)), we found that two decision variables are in the forms of T -1, T, n -1 T, and nT -1. Let y 1, y 2, y 3, y 4, and y 5 represent the following:
Then, E[TCU(T, n)] becomes the following:
We rearrange Equation (9) as follows:
Equation (10) indicates that if both the 2nd and 3rd terms are zeros, then E[TCU(T, n)] is minimized. Therefore, by substituting y 2, y 3, y 4, and y 5 in Eq. (10), we have
3.1.2 Phase 2: deciding T*
Once n has been decided, reconsidering E[TCU(T, n)] as a function of the single decision variable. Therefore, we can rearrange Eq. (9) as follows:
and Eq. (12) can be rearranged further as
Now, if the 2nd term of Eq. (13) equals to zero, then E[TCU(T, n)] will be minimized. That is
By substituting y 2, y 3, y 4, and y 5 in Eq. (14), we obtain
It is noted that the above equations (11) and (15) are identical to the results derived by Chiu et al. (2016). Using the same solution procedure as proposed in Chiu et al. (2016), E[TCU(T, n)] of this particular system can also be gained.
4. Conclusion
A multiproduct fabrication-shipment problem with postponement and product quality reassurance was studied by Chiu et al. (2016) employing mathematical modeling and calculus to derive the optimal operating decisions. This study proposes a two-phase algebraic method in lieu of the derivatives they used to show that the same solutions can be gained without applying the derivatives. This simplified approach aims at helping practitioners in the fields (who may lack of knowledge in calculus), better comprehend and manage such a particular fabrication-shipment system.
