1. Introduction
The Vertex Bisection Problem (VBP) is an NP-hard combinatorial optimization problem (Brandes & Fleischer, 2009). It consists in partitioning the set of vertices of a generic graph into two subsets A and B of approximately the same cardinality in such a way that the number of vertices in A with one or more adjacent vertices in B is minimized. Figure 1 illustrates the previous definition.
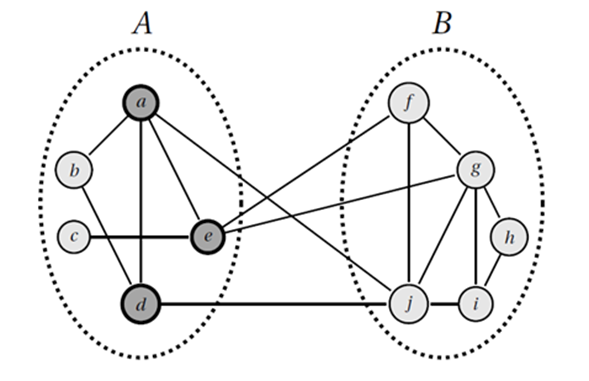
Figure 1 Example of one particular solution for the Vertex Bisection Problem. Vertices a , d and e contributes to the objective value of this solution.
In Figure 1 we show a particular solution for VBP over a
generic graph with ten vertices and sixteen edges. In this solution, the graph is
partitioned into the sets
The Vertex Bisection Problem has important practical applications in the telecommunication industry. In particular, VBP is relevant to fault-tolerance, and is closely related to the complexity of sending messages to processors in interconnection networks via vertex-disjoint paths (Klasing, 1998). Perhaps, the most representative application of VBP is in the gossip technique (Terán-Villanueva et al., 2019). In the context of communication networks, the gossip consists in dividing the network into two subnetworks in such a way that a minimum number of selected devices in the first subnetwork must have a connection to the devices of the second subnetwork. Thus, when a message must be sent to all members of the network, the message is exclusively disseminated by the selected devices of the first subnetwork. Since the number of selected devices of the first subnetwork is minimum, the resources consumption for this task is also minimum.
As stated previously, the Vertex Bisection Problem is important and computationally intractable. A significant research effort has been made to solve this problem. In the literature we can find both exact and approximate solution methods. Regarding the exact methods, seven approaches have been proposed for VBP, five Integer Linear Programming (ILP) formulations (Castillo-García & Hernández, 2019; Fraire et al., 2014; Jain, Saran & Srivastava, 2016a) and two branch and bound algorithms (Fraire et al., 2014; Jain, Saran, & Srivastava, 2016b). In addition, there are three metaheuristic algorithms (Herrán, Colmenar, & Duarte, 2019; Jain, Saran & 2016c; Terán-Villanueva et al., 2019) and one constructive algorithm for VBP (González et al., 2015), totalizing four approximate solutions.
The constructive heuristic proposed by González et al. (2015) is based on the Greedy Randomized Adaptive Search Procedure (GRASP) methodology (Duarte, Pantrigo, & Gallego, 2007). This algorithm adjusts (in execution time) the value of the parameter α by means of a small fuzzy inference system. In the context of GRASP, α is used to control the greediness level of the algorithm. Throughout this article, we will refer to this constructive algorithm as LIT since we will use it as a reference from the literature.
In this article we propose a new constructive algorithm based on the GRASP methodology. We call our constructive algorithm CVBP. The main difference between CVBP and LIT lies in the way in which they compute the objective value. LIT computes the objective value according to the traditional definition, that is, from the vertices in the set A (see Figure 1). Conversely, CVBP uses the redefinition of the objective function proposed by Castillo-García and Hernández (2019). This means that CVBP computes the objective value from the vertices in the set B. The formal definition of the traditional and the redefined objective functions can be found in Equations (1) and (2) of Section 2, respectively.
We conducted two computational experiments for assessing the performance of CVBP in practice. The first experiment was designed to fine-tune the parameter α of CVBP. Unlike LIT, CVBP does not modify the value of α during its execution. The experimental results showed that the best value for α is 0.0. This implies that CVBP is completely greedy. In the second experiment the best configuration of CVBP solved the entire benchmark of VBP consisting of 477 graphs of different classes and sizes (Castillo-García & Hernández, 2019). We also execute a random algorithm (RND) over the whole set of benchmark instances. The experimental data clearly showed that CVBP outperformed RND by 73.53 % in the quality of solutions found. In addition, we compare the results of CVBP and RND with those of LIT explicitly reported by González et al. (2015). The experimental evidence strongly showed that CVBP outperforms both RND and LIT by 76.19 % and 75.83 %, respectively. The superiority of CVBP was confirmed by the Wilcoxon Signed Rank Sum Test (Wilcoxon, 1945). The test found statistical significance between CVBP and LIT and between CVBP and RND for a confidence level of 99.99 %. Moreover, the test does not find statistical significance between RND and LIT.
The remainder of this article is organized as follows. Section 2 presents the formal definition of the Vertex Bisection Problem. Section 3 describes our proposed constructive algorithm CVBP in detail. In Section 4 we report the computational experiments carried out to assess the performance of CVBP in practice. Finally, in Section 5 we discuss the main conclusions of this research.
2. Formal Definition of VBP
Let
Let
Alternatively, the objective value of VBP can be computed from the vertices in the set B according to Equation (2) (Castillo-García & Hernández, 2019):
where
The goal of VBP is to find the partition P * such that its objective value is the minimum. In mathematical terms:
where SS stands for the solution space and its cardinality is given by the following binomial coefficient:
3. Constructive algorithm CVBP
Our constructive algorithm CVBP is based on the Greedy Randomized Adaptive Search Procedure
(GRASP) methodology (Duarte et al., 2007).
CVBP starts by assigning all the vertices to the set A
and no vertex to the set B, i.e.,
The first step of CVBP is to select the vertex
Notice that the greedy function g is actually the partial objective value of partition P computed by Equation (2) with the current members of A and B. Once all the vertices in A have been evaluated, CVBP selects a subset of candidate vertices known as Restricted Candidate List (RCL). The vertices in RCL are those whose g-value is less than or equal to the threshold
where min and max are respectively the lowest and the
largest g-values from the vertices in A, and
The vertex to be moved to set B is selected randomly from the
vertices in RCL. Like in the first step, sets A and
B must be updated. CVBP ends its execution
when the number of vertices in B is
| Algorithm 1 Constructive algorithm CVBP |
| 1: Input: A generic graph G= (V,E) and the value of |
| 2: Output: A partition P=(A,B) of G. |
| 3: |
| 4: |
| 5: |
| 6: repeat |
| 7: |
| 8: |
| 9: |
| 10: Select vertex |
| 11: |
| 12: until |
4. Computational experiments
In this section we report two computational experiments conducted to assess the performance of CVBP in practice. The first experiment aims at fine-tuning the parameter α of CVBP. This experiment is described in Section 4.2. In the second experiment, CVBP solves the entire set of 477 benchmark instances for VBP. This benchmark is the one used to evaluate the integer linear programming formulations proposed by Castillo-García and Hernández (2019) and consists of thirteen different kind of graphs. For comparative purposes, we also execute a random algorithm (RND) over the entire benchmark. The results of this experiment are reported in Section 4.3. In addition, in Section 4.4 we compare CVBP with both RND and the previously published constructive algorithm from the literature (LIT) over a subset of benchmark instances. More precisely, we compare the results obtained by CVBP and RND in the second experiment with the best results explicitly reported by González et al. (2015). Moreover, the comparison of CVBP, RND and LIT has been statistically validated through the Wilcoxon Signed Rank Sum Test (Wilcoxon, 1945). In the following section (Section 4.1) we describe the experimental conditions and the set of instances used in the experiments.
4.1. Experimental conditions and test bed
All the experiments were conducted on a standard computer with an Intel(R) Core(TM) i7-7500 CPU at 2.7 GHz and 32 GB of RAM. We implement CVBP and RND in Java (JRE 1.8.0_121) under the Microsoft Windows 10© operating system. As mentioned previously, we use a total number of 477 benchmark instances for VBP. These instances are grouped by classes of graphs in the following 13 datasets (Castillo-García & Hernández, 2019):
1.- Grid: This dataset consists of 52 graphs whose structure resembles two-dimensional square meshes. A grid graph can be drawn as a square mesh with c columns and r rows. The graphs in this dataset have the same number of rows and columns, i.e., c = r. The numbers of vertices and edges of these graphs range from 9 to 2,916 and from 12 to 5,724, respectively.
2.- Tree: This dataset consists of 50 trees. A tree graph can be informally defined as a complete graph without loops. Furthermore, a tree with n vertices has exactly n-1 edges. The numbers of vertices and edges of the trees in this dataset range from 22 to 202 and from 21 to 201, respectively.
3.- HB: This dataset has 62 graphs obtained from the well-known Harwell-Boeing Sparse Matrix
Collection. In this dataset, there is an edge from vertex
i to vertex j if
entry (i,j) of the
corresponding matrix is nonzero, i.e.,
4.- 2-dimensional mesh: This dataset contains 29 mesh graphs in two dimensions. The graphs in this dataset are the cartesian product of two paths:
5.- 2-dimensional toroidal mesh: This dataset contains 29 toroidal mesh graphs in two dimensions. These graphs are obtained by the cartesian product of two cycles:
6.- 3-dimensional toroidal mesh: This dataset consists of 18 toroidal mesh graphs in three dimensions. Like two-dimensional toroidal graphs, these graphs are the cartesian product of three cycles:
7.- Complete bipartite: This dataset consists of 32 complete bipartite graphs. The structure
of a complete bipartite graph
8.- Complete split: This dataset has 33 complete split graphs. A graph is complete split
9.- Harwell-Boeing: This dataset contains 36 graphs derived from the public domain SuiteSparse Matrix Collection (https://sparse.tamu.edu/).
10.- Hypercube: This dataset consists of 8 hypercube graphs. A
d-dimensional hypercube graph
11.- Join of hypercubes: This dataset contains 24 graphs resulting from the union of two
hypercubes and the addition of new edges. Formally, the join of two hypercubes
12.- Random: This dataset consists of 20 graphs generated at random.
13.- Small: This dataset consists of 84 graphs with a relatively small number of vertices and edges. Specifically, the numbers of vertices and edges of these graphs range from 16 to 24 and from 18 to 49, respectively.
4.2. Experiment 1: Fine-tuning CVBP
As mentioned in Section 3, the parameter
The reason for selecting the values of S is that they are
uniformly distributed in the interval
The test confirmed that the values of S are uniformly distributed with a confidence level of 95 %.
The experiment consists in executing CVBP with the
Table 1 Experimental results for different values of the parameter
|
|
O.V. | Time | RCL size statistics | ||||
|
|
|
|
|
|
|||
| 0.0 | 31.70 | 2.27 | 2.94 | 41.08 | 38.15 | 8.71 | 7.56 |
| 0.1 | 38.53 | 2.34 | 12.45 | 64.17 | 51.73 | 30.14 | 13.90 |
| 0.2 | 42.68 | 2.33 | 17.37 | 70.63 | 53.26 | 38.88 | 14.59 |
| 0.3 | 50.80 | 2.29 | 23.77 | 81.53 | 57.76 | 50.70 | 16.03 |
| 0.4 | 60.01 | 2.27 | 31.74 | 94.02 | 62.28 | 63.92 | 16.97 |
| 0.5 | 66.94 | 2.35 | 36.91 | 108.10 | 71.19 | 74.44 | 19.34 |
| 0.6 | 88.70 | 2.29 | 41.13 | 141.07 | 99.94 | 99.40 | 27.57 |
| 0.7 | 91.76 | 2.44 | 48.41 | 150.29 | 101.87 | 108.06 | 27.18 |
| 0.8 | 117.56 | 2.35 | 65.97 | 188.48 | 122.52 | 145.70 | 31.87 |
| 0.9 | 117.10 | 2.36 | 67.90 | 192.63 | 124.73 | 148.20 | 32.97 |
| 1.0 | 149.32 | 3.32 | 159.87 | 316.43 | 156.55 | 237.65 | 45.49 |
From Table 1 we can observe that the best value for the parameter α is 0.0. As mentioned previously, when α=0.0 CVBP becomes completely greedy. This means that, with this configuration, the RCL only contains those vertices whose greedy value is the minimum. The results also show that as the value of α increases, the quality of the solutions found by CVBP decreases considerably. The experimental results also show that the average execution time of the configurations is very similar to each other except for the last configuration (α=1.0). In fact, the differences observed are so small that we conclude that the α-value does not have any significant effect on the execution time. Finally, the results also reveal that the size of the restricted candidate list is affected by the value of α. According to the data, small values of α require small RCLs while large values of α require big RCLs. Notice that this tendency is similar to that observed in the average objective value. In order for the reader to observe this similarity clearly, we plot the average objective value and the average RCL size for each value of α in Figure 2. Specifically, Figure 2a exhibits the rising tendency of the average objective value (y-axis) as the value of α augments (x-axis). Similarly, Figure 2b depicts a series of 11 box plots that represent the sizes of the RCL with respect to the α-values. At this point it is evident that the best value for α is 0.0. This is so because it leads to a better solution quality and a small-sized restricted candidate list, on average. Therefore, we will use α=0.0 in the remaining experiment.
Furthermore, since the best value for α is 0.0, Equation (3) and line 8 of Algorithm 1 can be reduced to k=min.
4.3. Experiment 2: Solving the benchmark instances
The goal of this experiment is to assess the performance of the best configuration of CVBP in
practice. The experiment consists in executing CVBP with
α=0.0 over the whole set of 477 benchmark
instances and measuring the efficiency (execution time) and effectiveness
(solution quality). For comparative purposes, we also execute a random algorithm
(RND) to solve the same instances. RND randomly selects one vertex of the graph
until
Table 2 Experimental results for CVBP and RND over the 477 benchmark instances.
| Algorithm | O.V. | Time |
| CVBP | 27.07 | 5.210 |
| RND | 102.29 | 0.007 |
As can be observed, CVBP obtained the best average objective value. Specifically, CVBP outperformed RND by 73.54 % in the O. V. statistic. This means that the solution quality found by CVBP is approximately 3.78 times better than that found by RND. Figure 3 plots the results of this experiment for CVBP and RND. The red line represents CVBP while the blue line represents RND. The x-axis shows the 477 instances evaluated in this experiment. These instances are sorted by number of vertices n in ascending order. The y-axis presents the objective value found for the instances. This axis is logarithmically scaled in order to clearly observe the differences between CVBP and RND in solution quality.
As expected, RND was the fastest algorithm in this experiment. Its average computing time is about 7 milliseconds per instance. The average computing time of CVBP was 5.21 seconds. This difference can be partially explained by the fact that CVBP is much more sophisticated than RND. This means that CVBP must perform significantly more computations than RND. Thus, the experimental evidence suggests that the best option to solve VBP is CVBP regardless of the execution time.
4.4. Comparison of CVBP, LIT and RND
In this section we compare CVBP with both the random algorithm of the previous experiment (RND) and the GRASP-based constructive algorithm from the literature proposed by González et al. (2015) (LIT). The comparison is conducted on a subset of 46 benchmark instances from the HB and Harwell-Boeing datasets. Table 3 reports the objective values found by RND, LIT and CVBP. This table has two main sections and each section has the following five columns: the instance name (Instance), the number of vertices (n), the objective value obtained by RND (RND), the best objective value obtained by LIT (LIT) and the objective value obtained by our heuristic (CVBP). It is important to mention that González et al. (2015) report three results for each instance. Thus, in order for this comparison to be as fair as possible, we assign LIT the best (minimum) result reported.
Table 3 Comparison of RND, LIT and CVBP over 46 benchmark instances.
| Instance | n | RND | LIT | CVBP | Instance | n | RND | LIT | CVBP | |
| 494_BUS | 494 | 161 | 154 | 26 | dwt234 | 117 | 43 | 31 | 9 | |
| 662_BUS | 662 | 213 | 226 | 58 | DWT__245 | 245 | 84 | 97 | 21 | |
| 685_BUS | 685 | 249 | 257 | 54 | DWT__310 | 310 | 115 | 138 | 8 | |
| arc_130 | 130 | 65 | 29 | 8 | DWT__361 | 361 | 161 | 162 | 14 | |
| ash_85 | 85 | 40 | 33 | 9 | DWT__419 | 419 | 192 | 196 | 24 | |
| BCSPWR01 | 39 | 13 | 7 | 5 | DWT__503 | 503 | 236 | 240 | 53 | |
| BCSPWR02 | 49 | 14 | 10 | 3 | DWT__592 | 592 | 252 | 276 | 29 | |
| BCSPWR03 | 118 | 43 | 36 | 8 | gent113 | 104 | 50 | 43 | 21 | |
| BCSPWR04 | 274 | 114 | 99 | 32 | gre_115 | 115 | 51 | 43 | 22 | |
| BCSPWR05 | 443 | 152 | 148 | 33 | gre_185 | 185 | 92 | 82 | 24 | |
| BCSSTK01 | 48 | 24 | 20 | 12 | impcol_b | 59 | 26 | 24 | 19 | |
| BCSSTK02 | 66 | 33 | 33 | 33 | impcol_c | 137 | 64 | 52 | 22 | |
| BCSSTK04 | 132 | 66 | 66 | 24 | lns_131 | 123 | 50 | 40 | 16 | |
| BCSSTK05 | 153 | 61 | 73 | 17 | NOS4 | 100 | 40 | 38 | 10 | |
| BCSSTK06 | 420 | 202 | 197 | 68 | NOS5 | 468 | 208 | 229 | 56 | |
| bcsstk_22 | 110 | 50 | 37 | 6 | NOS6 | 675 | 244 | 279 | 27 | |
| CAN__144 | 144 | 71 | 59 | 6 | PLAT362 | 362 | 181 | 174 | 44 | |
| CAN__161 | 161 | 76 | 71 | 16 | steam03 | 80 | 40 | 36 | 4 | |
| CAN__292 | 292 | 114 | 124 | 27 | west0132 | 132 | 65 | 52 | 26 | |
| CAN__445 | 445 | 188 | 206 | 53 | west0156 | 156 | 76 | 65 | 30 | |
| curtis_54 | 54 | 27 | 17 | 7 | west0167 | 167 | 82 | 71 | 19 | |
| DWT__209 | 209 | 88 | 91 | 27 | will_57 | 57 | 23 | 17 | 5 | |
| DWT__221 | 221 | 103 | 98 | 7 | will199 | 199 | 95 | 91 | 62 |
As can be observed in Table 3, CVBP consistently obtained the best results for all the instances. The average objective values of CVBP, LIT and RND are respectively 24.00, 99.28 and 100.80. This means that CVBP outperformed LIT by 75.83 % and RND by 76.19 %. The data also reveal that the performance of RND and LIT in terms of average solution quality is similar. This tendency can be observed in Figure 4. In this figure the red line represents LIT, the blue line represents RND and the black line represents CVBP. The x-axis presents the instances sorted by number of vertices in ascending order. The y-axis shows the objective values obtained for each instance. This axis is logarithmically scaled in order to observe the tendencies clearly.
We conduct the Wilcoxon Signed Rank Sum Test (Wilcoxon, 1945) in order to determine whether or not the differences observed in solution quality are statistically significant. We use the statistical software R for conducting the test automatically. The results of the Wilcoxon test are reported in Table 4.
Table 4 Results of the Wilcoxon test over the solution quality of CVBP, LIT and RND.
| p-value | confidence level | significant? | |
| CVBP vs LIT | 2.675 x 10-9 | 99.99 % | YES |
| CVBP vs RND | 2.674 x 10-9 | 99.99% | YES |
| LIT vs RND | 0.08404 | 91.59 % | NO |
As we can observe, the test found a significant difference between CVBP and LIT with a
confidence level of 99.99 %. Similarly, the difference between CVBP and RND is
also significant with a confidence level of 99.99 %. This means that the
statistical test validates that CVBP outperformed both LIT and RND in
effectiveness. The Wilcoxon test also determine that the difference between LIT
and RND is not significant. This is so because the
p-value found was greater than the standard
threshold used in scientific research, i.e.,
5. Conclusions
In this article we have faced the Vertex Bisection Problem (VBP). The problem asks for a partition of the set of vertices of a generic graph into two subsets (A and B) with approximately the same cardinality. The goal is to minimize the number of vertices in A with one or more adjacent vertices in B. In particular, we have proposed a new constructive algorithm (CVBP) based on the Greedy Randomized Adaptive Search Procedure (GRASP) methodology. We conducted two computational experiments to assess the performance of CVBP in practice. The first experiment was designed to fine-tune the parameter α of CVBP by solving a representative sample of the benchmark instances. The experimental data clearly indicate that the best value for the parameter α is 0.0. Thus, Equation (3) and line 8 of Algorithm 1 can be reduced to k=min, which indicates that CVBP is completely greedy.
In the second experiment we solve the entire set of 477 benchmark instances and compare CVBP with a random algorithm (RND). RND is a constructive algorithm that iteratively selects one vertex without any kind of criterion at all. The experimental results clearly suggest that CVBP is the best option in terms of solution quality. Specifically, CVBP outperformed RND by 73.53 % in average objective value. In addition, we compare the results of CVBP and RND with a previously proposed constructive algorithm (LIT) (González et al., 2015). The data showed that CVBP outperforms both RND and LIT by 76.19 % and 75.83 %, respectively. This fact was confirmed by the Wilcoxon Signed Rank Sum Test (Wilcoxon, 1945). The test found statistical significance between CVBP and LIT for a confidence level of 99.99 %. Likewise, the difference between CVBP and RND is significant for a confidence level of 99.99 %. Although LIT slightly outperformed RND by 1.51 %, the difference is not statistically significant to conclude that LIT is superior to RND.
Therefore, taking into account the experimental evidence and the statistical validation, we conclude that CVBP is a good alternative to stochastically solve the Vertex Bisection Problem. Moreover, CVBP can be coupled with a local search or embedded in a larger framework (e.g., a metaheuristic algorithm) in order to obtain better results for the problem.











 nueva página del texto (beta)
nueva página del texto (beta)





