1. Introduction
Operating in extremely competitive global markets, managers of today’s manufacturing firms must constantly seek alternatives to strengthen their firms’ competitive forces, such operating strategies include (i) to increase of utilization by planning multiproduct fabrication on a single machine; (ii) to adopt the delayed product differentiation policy when common parts exist; (iii) to implement the strategy of flexible capacities, such as overtime, to expedite its production, etc. This study is motivated and intended to address these real factors. Their related literature is surveyed as follows. The increase of machine utilization can be achieved through planning multiproduct fabrication in sequence on a single machine. Zipkin (1986) presented an approach to model a manufacturing facility that produces diverse items in large, discrete lots, with demands and the production process being both stochastic. His work incorporated standard inventory and queueing sub-models into classical optimization problems. Aragone and Gonzalez (1997) proposed a numerical approach to study a single-machine multiproduct scheduling problem. Authors presented a discretion method and a computation procedure to find the solution with a precision of discretionary order size in a short period of time. Balkhi and Foul (2009) investigated a multi-item backlogging fabrication-inventory system within finite given time periods. They attempted to determine the optimal manufacturing and restarting times for each item per cycle to minimize the overall system costs. Extra studies (Chiu, Kuo, Chiu, & Hsieh, 2016; Chiu, Chiu, Lin, & Chang, 2019; He, Wu, & Zhang, 2018; Huang, & Ma, 2014; Lin, Wu, Gong, Mehdizadeh, Gholami, Naderi 2018; Matsuyama, 1992; Nahmias, 2009; Rosenblatt & Finger, 1983; Wolsey, 2002) focused on diverse aspects of optimization and fabrication planning of multi-item fabrication.
The delayed differentiation strategy refers to a common intermediate product existing in a multi-item manufacturing system, managers often are interested in evaluating diverse manufacturing schemes, such as redesigning a two-stage production process to delay differentiation, wherein all the required common parts per cycle are fabricated in stage 1, and the customized end products are made in stage 2, using a rotation cycle length policy. With this strategy, production managers are able to rapidly respond to the customers’ demands and/or reduce overall production-inventory cost. Hence, it is an effective strategy from the standpoint of reducing inventory and/or improving service level. Swaminathan and Tayur (1999) specified an approach to increase the producer’s competitive advantages by integrating the products’ design and operation for a variety of products in one production line. The authors claimed that the manufacturers could achieve an effective response to the client’s needs by refining assembly sequence. Motivated by this concept, the authors proposed a few integrated models to promote operational benefits. Through computational illustrations, such as the influence of demand variation, life cycles, and setup times for the optimal design of assembly arrangement, they provided the qualitative insights on the aforementioned issues. Graman and Magazine (2006) survey corporation managers for their opinions to identify the key subjects that may have a positive impact on implementing the postponement strategy. The authors found that diverse matters were linked to the implementation of a partial postponement policy than reposition of stock levels as suggested by several mathematical models. The authors recognized certain critical issues, such as product integrity, administrative readiness, and operations scheduling, have a greater influence on the postponement implementation. Additional works (Ahranjani & Matin, 2018; Cavusoglu, Cavusoglu, & Raghunathan, 2012; Davis & Sasser, 1995; Oladapo, Balogun, Adeoye, Olubunmi, & Afolabi, 2017; Rushdi, 2019; Sheikh, Komaki, Kayvanfar, & Teymourian, 2019) focused on diverse aspects of implementing the postponement strategies.
Strategies of flexible capacities are constantly used to deal with potential short supply of in-house capacity or to effectively shorten the fabrication cycle time. Such as an overtime option, through working 2 or 3 shifts per day, or adding a partial shift (e.g., a few hours of overtime), it can effectively boosts the output rates, thus, it increases the in-house capacity. Dixon, Elder, Rand, and Silver (1983) studied the lot size and replenishing timing for a fabrication system under the known but time-varying demands and no allowable stock-out situations. The authors considered flexible regular time and overtime options with time-varying capacities in each option. Their work aimed at deciding the optimal batch size for each replenishing time in terms of system cost minimization. The heuristic algorithm was proposed to test enormous sets of problems to demonstrate their algorithm’s excellent performance in solving the problems. Yura (1994) explored a fabrication scheduling problem which aimed at concurrently meeting the workers’ preferences in the selection of working times and due-date conditions. Because of the heavy workloads, from time to time, there may not be a feasible solution to meet all the workers’ preferences. Hence, the goal of scheduling becomes to minimize necessary overtime that satisfies the workers’ preferences. The author used linear goal programming techniques in the solution process for the problem along with numerical illustrations to show the applicability of the result as well as the types of analytical outcomes. Zobolas, Tarantilis, and Ioannou (2008) improved the MPS (i.e., master production schedule) for the make-to-order manufacturing systems with excessive demand. An algorithm was presented to incorporate diverse constraints, such as fabrication sequences guided by overtime penalties, earliness, and tardiness for resolving the problem. An intermediate tool-rough cut capacity plan featuring overtime, earliness, tardiness, and lead time was used to decide the use of the resources. The authors used the genetic algorithm to help solving their model, and diverse real-data benchmarking problems were tested to exhibit the performance of their model. Extra studies (Chiu, Chen, Chiu, & Chiu, 2018; Chiu, Wu, Chiu, & Hwang, 2018; Chiu, Wu, & Tseng, 2019; Golden & Wiens-Tuers, 2008; MohanDas, Ayyanar, Susaiyappan, & Kalimuthu, 2017; Özdamar & Bozyel, 2000; Rao & Singh, 2018; Singer & Obach, 2013) examined the impacts of the characteristics of overtime options or adjustable output rates on enterprises as well as on different fabrication systems.
2. Materials and Methods
2.1. Problem assumption, description, and modelling
The basic assumptions in this proposed two-stage multiproduct fabrication system include (a) it is an extended multiproduct EMQ-based system; (b) it has a known completion rate of common intermediate part (comparing to the end product), (c) demand rates per year of these products are constant; (d) in stage 1 of the fabrication, the common parts of multiproducts are produced under an overtime strategy; (e) in stage 2 of the fabrication, annual production rates of multiproducts depend on the completion rate γ of the common part, e.g., if γ = 50%, then the manufacturing rate of the end product becomes double the standard rate of a single stage manufacturing system; and (f), it has a continuous stock depleting policy.
The model has the following detailed description: the annual demand rate for each multiproduct i is λi; and in stage 1 of the production, all the common intermediate products needed are made first; then, in stage 2, the customized L finished products are made in sequence using a rotation cycle time discipline (see Figure 1), at a standard rate of P1,i (where i = 1, 2, …, L).
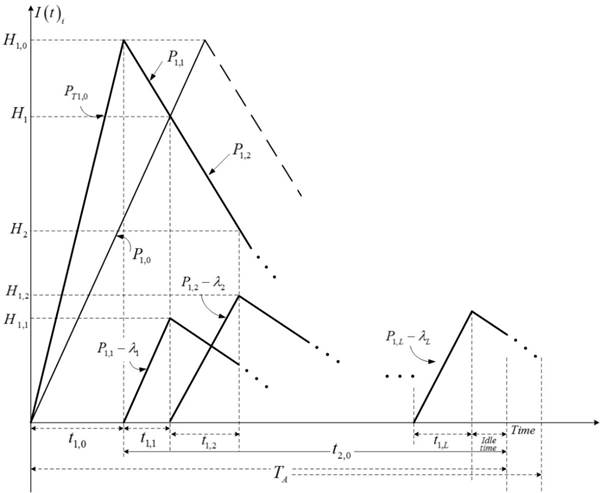
Figure 1 The perfect stock level in the proposed two-stage multiproduct EMQ-based system with delayed differentiation and overtime option for the fabrication of common parts as compared to a system with overtime option.
In the proposed delayed differentiation two-stage multiproduct EMQ-based system, it is true that the fabrication of common parts in the first production stage takes up a large share of the cycle time, to shorten the cycle length, an overtime option is considered in stage 1. For instance, working 2 or 3 shifts per day, or adding a partial shift (e.g., a few hours of overtime). This option is especially effective to boost the output rates for the fabrication of common parts, so the production time in stage 1 can be significantly reduced, so can the common production cycle time, at the price of higher production setup and unit manufacturing cost because of the overtime option. It is assumed that the following higher setup cost K T0 and unit production cost C T0 are associated with the adoption of the overtime option for the production of common parts, and the system now has a faster rate P T1,0 to produce common parts.
where P 1,0, K 0 , C 0, and αi,0 represent the first stage’s standard rate, setup cost, unit production cost, and the linking factors among these overtime-related and standard variables, respectively. For example, α1,0 = 0.5, the production rate for common parts, is 50% higher than standard because of overtime, and α3,0 = 0.25, the unit production cost, is 25% higher than the standard unit cost due to overtime, etc. To avoid shortages, in stage 2, it is assumed that P 1,i - λi > 0 (where i = 1, 2, …, L). The cost parameters of this model include: setup cost K i and holding cost h 1,i . The following extra notation is used:
γ common part’s completion rate (comparing to the finished item),
Q 0 lot size for the common parts in stage 1,
t 1,0 uptime for producing the common parts with the overtime option,
H 1,0 the stock level of common parts when the regular production ends,
λ0 annual demand rate of the common parts,
Q i lot size for end product i,
C i unit fabrication cost for product i in stage 2 (where i = 1, 2, …, L),
t 1,I fabrication uptime for product i,
t 2,I time required to deplete all items of product i,
T A rotation cycle time - decision variable,
H 1,I the stock level of product i when production ends,
H i stock level of common parts when production of product i ends,
I(t) I stock level at time t of product i,
i 0 holding cost relating ratio, i.e., h 1,i = (i 0)C i ,
t 0 * the optimal uptime for making common parts with overtime option in stage 1,
t i * the sum of optimal uptimes for fabricating each end item in stage 2,
TC(T A) =total fabrication-inventory costs per cycle,
TCU(T A ) = the long-run average system costs per unit time.
2.2. Formulation of the proposed system
2.2.1. Formulation in stage 2
In stage 2 of the proposed system, the following formulas (for i = 1, 2, …, L) can be directly observed from Figure 1:
2.2.2. Formulation in stage 1
In stage 1 of the proposed multiproduct fabrication system, the following formulas can also be directly observed from Figure 1:
2.2.3. Total cost per cycle
The total system’s costs per cycle, TC(T A) consist of the first stage’s variable manufacturing, setup, and the holding costs for the common parts; and the second’s stage sum of the variable manufacturing, setup, and the holding costs for L distinct customized end products. Therefore, TC(T A) is as follows:
The substitution of Q i by T A (i.e., Eq. (4)) in Eq. (14) becomes as follows:
2.3. Prerequisite condition of the proposed system
To ensure that a machine in the proposed multi-product system has sufficient capacity to produce the common parts and L different end products under the common cycle time policy (Nahmias, 2009), the prerequisite condition as shown in Eq. (16) must hold:
3. Results and Discussions
3.1 Deciding the optimal TA*
By substituting the aforementioned Equations (1) to (13) in Equation (14) along with extra derivations, we have the following TCU(T A):
The 1st and 2nd derivatives of TCU(T A) can be obtained as shown in Eqs. (18) and (19). It can be observed that all the parameters in the right-hand side (RHS) of Eq. (19) are positive; therefore, TCU(T A) is convex. Hence, the optimal T A * can be solved by setting the first-derivative of TCU(T A) = 0 along with an extra derivation, by doing this, the result is the optimal T A * as shown in Eq. (20).
An important fact to be noted is that the summation of L distinct end products’ setup times has a positive influence on the aforementioned optimal T A * when it cannot be fitted into the idle time of the system (refer to the idle time of Fig. 1). In that case, the following T min (Nahmias, 2009) must be computed and the max(T min, T A *) selected as the final optimal T A solution to the problem to ensure the cycle time is sufficient to comprise all the required setup and fabrication times in both stages.
3.2. Numerical example
Consider that the demands of five different products must be satisfied by the proposed two-stage multiproduct fabrication decision with delayed differentiation and the overtime option for the fabrication of common parts. The assumption of original variables in a one-stage system is listed in Table 1, and a set of separate parameters for stage one and two of our proposed two-stage multiproduct system is given in Table 2(a) and Table 2(b).
Table 2(a) Values of parameters used in stage one.
| γ | P1,0 | α1,0 | δ | C0 | K0 | λ0 | h1,0 | i0 | α2,0 | α3,0 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 120000 | 0.5 | 50% | $40 | 8500 | 17406 | $8 | 0.2 | 0.1 | 0.25 |
Apply Eqs. (20) and (17) from Section 3, we obtain the optimal cycle time T A * = 0.5568 and the TCU(T A*) = $2,094,210 for our two-stage multiproduct EMQ-based system.
3.2.1. Convexity of TCU(TA*)
A further analysis on the convexity of TCU(T A*) was performed; its result is shown in Figure 2. The result confirms that as the cycle length deviates from T A*, TCU(T A*), it increases significantly.
3.2.2. The effect on the machine utilization
Because of the use of the overtime strategy on the fabrication of the common parts, the effect of the overtime factor on the uptime of stage 1 was explored; the result is illustrated in Figure 3. This result indicates that the optimal uptime for fabricating common parts in stage 1, t 0* drops from 0.0780 to 0.0526 (years) because of 50% overtime usage, i.e., it is a 32.24% decrease in utilization in stage 1.
3.2.3. The combined effect of diverse system parameters on TCU(TA*)
The combined effect of differences in diverse system parameters on TCU(T A*) were explicitly explored; the result is displayed in Figure 4. The result demonstrates that although TCU(T A*) increases as both the overtime factor α1,0 and the common part’s completion rate γ rise; the joint impact is extremely significant when both α1,0 and γ are higher.
3.2.4. The impact of diverse system parameters on TA*
Additional analysis on the joint impact of changes on diverse system parameters on T A* is performed; Figure 5 shows the result which reveals that T A* declines significantly as the completion rate γ of the common part increases; and T A* changes slightly, as the overtime factor α1,0 rises, especially when γ is smaller. But, T A* goes up gradually, as the overtime factor α1,0 increases, particularly when γ is larger.
4. Conclusions
This study aims to explore the two-stage multi-product fabrication decision incorporating delayed product differentiation, an overtime option for the production of common parts, and continuous end-item issuing policy. We carefully built a mathematical model to depict and examine the problem; through the help from the renewal reward theorem and the optimization technique, an optimal rotation cycle time solution is achieved. We provide an example to show the applicability of our investigated outcomes. In addition to the gain in the optimal cycle length, the main contribution of this study also includes exposing the individual and combined influence of crucial system parameters on the optimal T A*, machine utilization, and TCU(T A*) of the problem (please, refer to Subsections 3.2.1. to 3.2.4.), these outcomes had never been discovered. The research results can facilitate managerial decision makings in such a real two-stage multiproduct system incorporating delayed product differentiation, an overtime option for the production of common parts, and product quality assurance. To examine the effect of combining an outsourcing strategy with the fabrication plan of common parts with the same problem will be an interesting future study.











 nueva página del texto (beta)
nueva página del texto (beta)






