2.1. Experimental setup

This experiment focused on the intermediate water gravity waves hL=0.15693, 0.35816, 0.47487. In this study, these waves were produced by using a mechanical force such as a motor-driven paddle at one side of a flume tank. The amplitude and frequency of the paddle can be controlled in the paddle drive system. The experiment detailed in this study was carried out in a wave tank at the fluid dynamic laboratory at Western Michigan University. The wave flume tank consists of a clear acrylic plexiglass channel with dimensions 7.32 m long, 0.15 m wide, and 0.36 m deep. The flume tank was divided into three equal sections, and the middle section was the test section. The schematic diagram of the wave flume tank can be seen in Figure 1.

Figure 1 Schematic diagram of the wave flume tank setup. PS1 & PS2 are denoted as the locations of the Honeywell pressure sensors mounted at the bottom of the wave flume tank. A1 is denoted as the test section at the water surface level, and h= 17 cm is denoted as the still water level. 

2.2. Wave parameter measurements

Mechanically driven wavemaker made of plexiglass hinged at the bottom of the flume tank with adjustable wave amplitude and wave frequency that produce sinusoidal wave motion. The electrical motor wave generator that was used to drive the Plexiglas flap wavemaker is composed of a ¼ HP, maximum 1725 RPM, 115 V, and 4.4 A. Electrical motor and a Plexiglas flap, see Figure 2.

Figure 2 Schematic diagram of the wave generator system. 

Waves were generated by a flap-type bottom-hinged paddle mounted at one end of the tank, which travels down the trough and is employed to dissipate smoothly on the slope of the beach, or it can be called a wave absorber, as seen in Figure 1. The paddle (wavemaker) was driven by an electrical motor. Various paddle motion was achieved by varying the rotational speed of the electrical motor.

Three methods were used to obtain wave height, wavelength, and period. Firstly, Honeywell pressure sensors were mounted at the bottom of the wave tank at two different locations: one at 1 m from the wavemaker (PS1) and the other at 5 m from the wavemaker (PS2) to get a fully developed wave, as shown in Figure 1. Wave height and period were obtained from pressure reading, and then the linear wave theory equation was implemented, especially dispersion relation to getting wavelength. Secondly, analyzed PIV images to obtain the values of wave height and wavelength. Finally, by assuming that the frequency of the wavemaker is the same as wave frequency, then the dispersion relation could be used to get wavelength and then use the transfer function of the flap wavemaker (the relationship between wave height and the wave paddle stroke) to get wave height.

3.1. Wave characteristics

Four parameters define characteristics of the gravity wave that are: height (H, m) or amplitude (a=H/2, m), length (L, m), period (T, sec) or angular wave frequency (ϖ, 1/sec), and wave steepness (H/L) or this parameter (H/T, m/sec). Wave height is the vertical distance between the crest and the trough. The amplitude is the distance from the still water level, also known as zero energy level (assumed to be at the center of the wave is the halfway between the crest and trough, h(m)), to the bottom of the trough or the top of the crest. Thus, the wave height is twice the wave amplitude. Wavelength is the horizontal distance between two successive troughs or crests. The wave period is the time required for one full wavelength to pass a given point. Where the wave frequency is the number of a wave crest or wave trough that passes a fixed point per unit of time and is the inverse of the period. Wave steepness is the ratio between wave height and wavelength, see Figure 3.

Figure 3 The wave of water parameters. 

Wind waves are classified according to the ratio between still water depth and wavelength (h/L). Thus, wind waves are considered as deep-water waves when the still water depth is greater than half of the wavelength h>L2 orhL>0.5, intermediate or transitional water waves when  L2>h>L20 or  0.5>hL>0.05, and shallow water waves when (h >L2 orhL>0.5) This study was concerned with intermediate water gravity waves (0.15693, 0.35816, 0.47487).

3.2. Linear gravity wave theory

Linear gravity wave theory, also known as the Airy wave theory, is defined as the most straightforward theory used to obtain equations that provide the kinematic and dynamic properties for a two-dimensional small-amplitude surface gravity wave. The linear wave theory assumes that the ratio of the wave height to wavelength is less than 1/7, which means small wave steepness. The main assumptions for the linear wave theory are as follow:

The most important assumption is the wave amplitude is small compared to the wave height and still water level.

3.2.1. Governing equations

1- Navier - stokes equation, as shown in Eq.1

Where ρ Kgm3  water density.  U, w msec water surface velocity in x and z direction, respectively.   

By ignoring the viscous force and expanding the above equation into two considered directions (x, z), the following two Euler equations are derived, respectively, as shown in Eq. 2 and 3:

2- Continuity equation, as shown in Eq. 4

Introduce the velocity potential function ϕx,t, as u=∂ϕ ∂x ,    w=∂ϕ ∂z  then substitute two of these formulas back into Eq. 2, 3, and 4, becomes as shown in Eq. 5 and 6

Integrate the above equation on (x, z) directions, respectively; the following Eq. 7 and 8 are obtained:

As shown above, the two force equations are precisely the same, but the second equation includes gravity effects. Therefore, a single equation for the whole field was developed and is known as the Bernoulli equation for unsteady irrotational flow, as shown in Eq. 9.

The continuity equation is transformed to the Laplace equation as follows in Eq. 10:

Defined Boundary conditions as follows:

1. The kinematic boundary conditions at the bottom of the wave tank. Based on the previous assumption, we assumed the bottom of the wave tank is not moving, as shown in Eq. 11.

2. The boundary condition at the water-free surface

a- Kinematic boundary condition related to the vertical velocity at the water-free surface, as shown in Eq. 12.

b- Dynamic boundary condition related to the pressure at the water-free surface, as shown in Eq. 13

The boundary condition at free water surface must be linearized and reapplied at still water level z= zero instead of z=η. This developed Eq. 14 and 15

Velocity potential function ϕ for small-amplitude surface gravity wave was derived by solving the LaPlace Eq. 10 using kinematic boundary condition at the bottom and the linearized dynamic boundary condition at the free water surface, as shown in Eq. 16.

Wave surface profile η was derived by inserting the velocity potential function into a linearized dynamic boundary condition, as shown in Eq. 17.

The dispersion relation is known as the relationship between the wave frequency and wavenumber at a given still water depth. It was derived by adding the two linearized boundary conditions at the free water surface (dynamic and kinematic) together, then applying velocity potential and differentiating. This yield Eq. 18.

3.3. Pressure under waves

Pressure under the still water level depends on two factors: hydrostatic pressure due to the depth of still water and the dynamic pressure caused by waves. The pressure at any water level can be obtained by applying the Bernoulli equation for unsteady irrotational flow, as shown in Eq. 19.

Since we are dealing with a linearized condition, the second-order term u2+w2 must be ignored, then inserting velocity potential function. This yields the following relation, Eq. 20:

The first term represents hydrostatic pressure, and the second term represents dynamic pressure (wave pressure). See Figure 4.

Figure 4 Pressure variation under the wave crest(^{Andersen & Frigaard, 2011}). 

4.1. Based on the theory of flap wavemaker

There are many ways used to generate regular waves such as piston type, flap (hinged) type, or plunger-type (^{Dean & Dalrymple, 1991}). In the present work, flap (Hinged) type was used to generate regular waves in the wave tank in the fluid dynamics lab at Western Michigan University. Wave paddle stroke is defined as the maximum stroke distance that can be traveled by flap wavemaker at the free water surface (S, cm). The stroke of the flap was adjusted from 5.43 cm at the still water level (17 cm) to 11.5 cm at the top of the wave tank (36 cm), see Figure 5. The flap was attached to the bottom of the wave tank by a hinge that allows the flap wave maker to move forward and backward with the rotation of the electrical motor, as was shown in Figure 2.

Figure 5 Schematic diagram of paddle flap wavemaker. 

Wave frequency, wavelength, and wave height were controlled by adjusting the stroke of the flap wavemaker and the frequency of the electrical motor. A digital photosensor tachometer was used to measure the electrical motor frequency with an accuracy of ±0.05%. To use the theory of flap wavemaker, the frequency of the wave paddle should be the same as the frequency of the wave generated. Thus, wave frequency was also measured by the time required for the 100 wave crests to pass a fixed point at 2 m far away from the wavemaker, using a stopwatch. Many wave crests were selected as the period of waves was up to 0.958 sec. So, it’s obvious that human error in measurements would be reduced if the time taken for passage of the 100 wave crests through a specific point were measured as opposed to say, for example, the ten wave crests. Hence, the accuracy in measurements of wave period increase with the number of waves under consideration (^{Saincher & Banerjee, 2015}). The result was very close, and the error between the two readings was between (0.048%, 0.035%, and zero), and that means the results could be used to apply the transfer function of the flap wavemaker, as follows in Eq.21, (^{Dean & Dalrymple, 1991}):

To use the Eq. 21, it should have the value of wavelength first. So, in this method, dispersion theory was used to get wavelength then substituted back into transfer function to get wave height. Thus, the wavelength cannot be directly solved for a given set of wave periods (T) or still water depth(h) from dispersion theory. Therefore, to get the wavelength value, it should be found by iteration. In this study, four numerical methods were used to get wavelength, as explained later.

4.2. Based on pressure measurements

In this study, two Honeywell pressure sensors were used to measure wave height. They were placed one and five meters away from the flap wavemaker. These sensors should not be placed directly at the water medium; thus, these sensors were fixed outside the wave tank and connected with a clear plastic tube, and that tube was tied and fixed at the bottom of the wave tank. These pressure sensors are designed to provide the outcome reading for the pressure. That means the outcome readings must be calibrated to obtain the actual readings of the pressure then turned to wave height by using Rayleigh distribution and zero down crossing method. Firstly, the two Honeywell pressure sensors must be calibrated to connect the measured value and actual pressure reading. The calibration test was done twice for two Honeywell pressure sensors. The calibration test was done by placing the pressure sensor as mentioned above, then changing the depth of still water above the pressure sensor. In the meantime, measured value (outcome from the pressure sensor) was recorded and calculated with the corresponding value of the actual hydrostatic pressure, as follows in Eq. 22:

Where ρ is defined as the density of water 1000Kgm3,g is defined as the gravitational acceleration of 9.81msec2 , and h(m) is defined as the depth of still water. The measured values and actual pressure readings at different still water depths are listed in Table 1.

Figure 6 Calibration correlation between a measured value and actual value. 

As seen in Figure 6, the correlation coefficient R2 is 0.9797 means there is a high correlation between measured and actual value. Thus, the calibration correlation is as follows in Eq. 23:

Where PmV is defined as the actual pressure readingPaand mV is defined as the outcome reading from the pressure sensor. After the value of the actual pressure under the waves was evaluated, the pressure value must be converted to wave height by applying the equation of total pressure that was derived above at Z=-h, like the following:

Maximum Pressure reading was measured at the crest at ηmax, as shown in Eq. 24 :

Minimum Pressure reading was measured at the Trough at ηmin, as shown in Eq. 25 :

Wave height is the difference between the maximum and minimum wave surface elevation ηmax-ηmin, shown in Figure 7.

Figure 7 Schematic diagram of wave height from a pressure measurement. 

Thus, Wave Height can be evaluated from Eq. 26.

As seen in the above equation, wave height is the function of wavenumber, k=2πL and its function of wavelength. Wave height and wave period were obtained by using the Rayleigh distribution and the zero-up crossing analysis method. Based on the results from the previous section, the Newton Raphson numerical method is the best equation that can be used to solve the dispersion relation with the smallest error. Thus, the wavelengthv was obtained vby using a dispersion relationship

that was solved by using the Newton Raphson numerical method. Two Matlab codes were built to avoid manual calculation and get an accurate value of wave height, as seen in the following Figures 8, 9, and 10, and were evaluated at three different wave frequencies. The significant wave height Hs obtained and is defined as the average height of the highest one-third of waves in a wave spectrum. The significant wave height is very often considered as the design wave. The comparison between the results was evaluated based on pressure measurement and the analyzed images captured using the PIV technique can be seen in the discussion section.

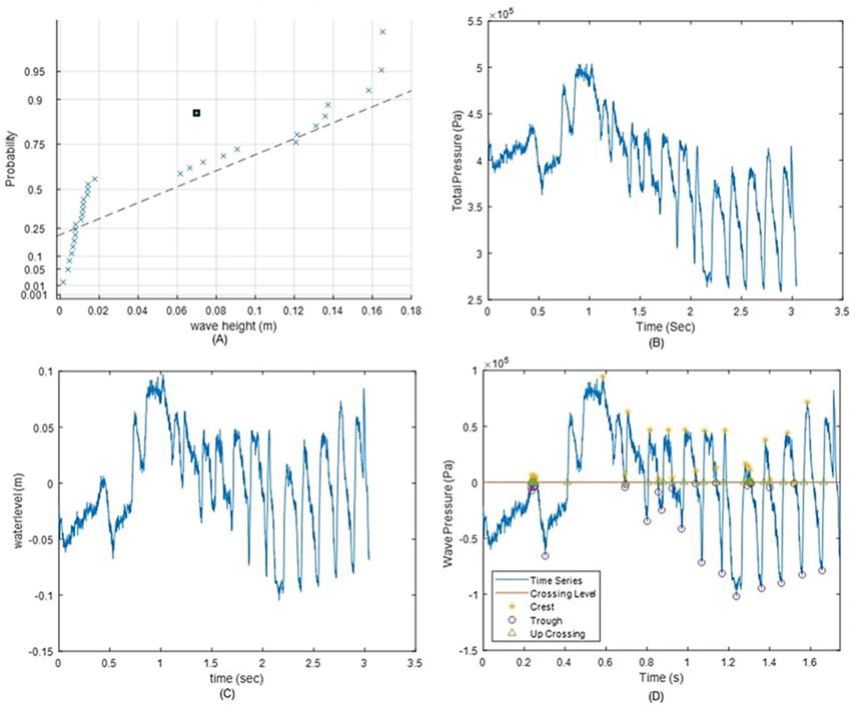
Figure 8 Wave record with a period of T=0.4771 Sec. A: The Rayleigh distribution of the pressure sensor, B: Total pressure caused by hydrostatic pressure and wave pressure, C: Wave surface profile η, D: Zero -up crossing applying on dynamic pressure caused by the wave. 

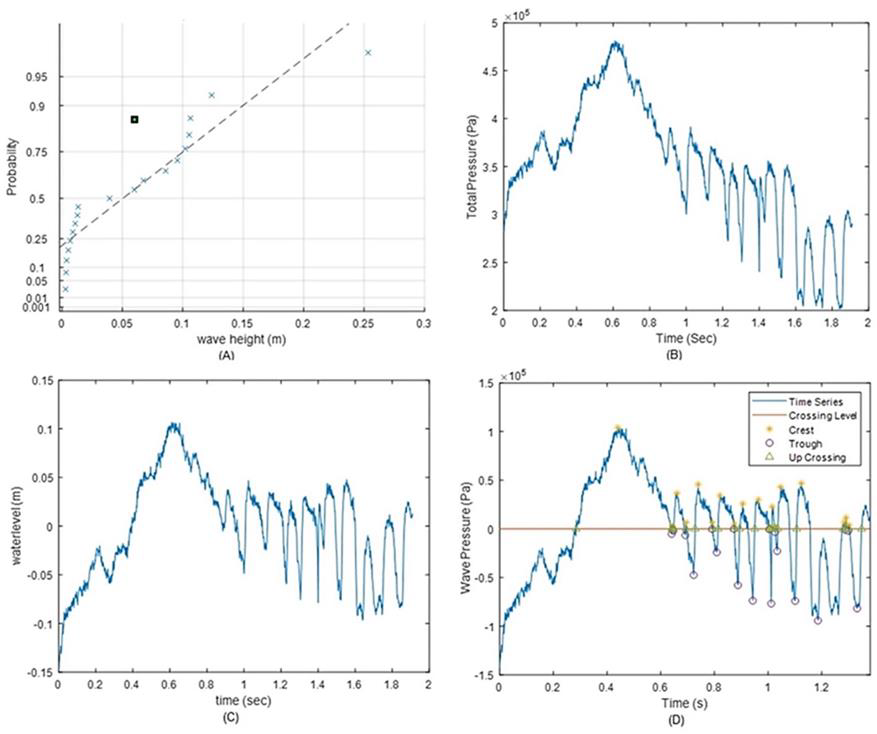
Figure 9 Wave record with a period of T=0.5576 Sec. A: The Rayleigh distribution of the pressure sensor, B: Total pressure caused by hydrostatic pressure and wave pressure, C: Wave surface profile η, D: Zero -up crossing applying on dynamic pressure caused by the wave. 

Figure 10 Wave record with a period of T=0.9585 Sec. A: The Rayleigh distribution of the pressure sensor, B: Total pressure caused by hydrostatic pressure and wave pressure, C: Wave surface profile η, D: Zero -up crossing applying on dynamic pressure caused by the wave. 

4.3. Based on PIV image (image processing)

4.3.1. PIV technique setup

The PIV setup is shown in Figure 11. A big sky double pulsed Nd: YAG (Neodymium-Doped Yttrium Aluminum Garnet) laser of wavelength 532 nm and 200 mJ/Pulse with the maximum repetition rate of 15 Hz per laser head was used to provide illumination of the seeding particles. The laser sheet adjustment is the most important step in PIV setup to obtain highly accurate results and safety issues. This was done using orange light-sensitive paper. That paper was placed in the front of the laser beam source in the middle of the flume tank (test section, the location where the laser sheet should be generated). The laser beam source was performed with a lower laser energy limit and was visible in the dark ambient light condition to ensure safety. The two laser beams sources should leave marks on the orange paper. One mark was found on the orange paper, which means two laser beams are hitting at the same point (^{LaVision GmbH, 2016}). The laser beam source was directed from above the flume tank towards the middle of the water surface using a 45( dielectric mirror, then a cylindrical lens was used to convert the laser beam into the laser sheet with a thickness is about 2 mm.

Figure 11 Schematic diagram of the PIV setup used in this experiment. 

The laser sheet was generated to be perpendicular to the water surface and parallel to the sidewall of the flume tank. The laser sheet was slightly inclined at a 6( downwind from the middle of the flume tank. LaVision charged coupled device (CCD)Imager Pro X 2m camera was used. The camera resolution is 1600 x 1200 pixels with a bit depth of 14 bit, and the pixel size is 7.4(m. The camera has a double exposure feature with an interframe time down to 100 ns, and the frame rate is 30 fps at full resolution. The camera is fitted with an adapter to connect it with a NIKON AF NIKKOR zoom lens (50 mm 1:1.8 D), which means the focal length is 50 mm, and the f- stop number is 1.8. Camera alignment is a critical issue that can affect the accuracy of the measurement. Thus, the CCD camera should be set with the optical axis perpendicular to the laser sheet. The misalignment between a CCD camera and the laser sheet produces a bias in the measurements (^{Kompenhans et al., 2002}; ^{Raffel et al., 1996}; ^{Scarano, 2013}). The camera was mounted in the front of the flume tank with a 6( inclined angle from the perpendicular axis, as shown in Figure 12.

Figure 12 Experimental setup of PIV. 

The calibration algorithm in Davis (8.4) was used to calibrate the CCD camera to make sure the camera was arranged perpendicular to the laser sheet. HGS-10 hollow glass sphere with diameter 10(m and the density of 1.10±0.05 g/cm3 from Dantec was used as the seeding particles, and it is known as the best particles for water flow (^{Scarano, 2013}). A synchronizer is a control unit that is used to provide external triggers for the CCD camera and the two pulsed laser sources. The synchronizer can be used to control the delay time between the two pulsed laser beams, which is known as synchronizer separation time ∆t, and the firing of two pulsed laser beams relative to CCD camera exposure. All these steps were controlled by Davis 8.4 from LaVision. The separation time ∆t is a critical parameter used to evaluate velocity components of the flow. Determining the optimal pulse separation time ∆t of the two-laser beam depends on the flow behavior and can be set manually by the user or automatically by Davis 8.4 based on the wanted particle shift.

This experiment was done at the fluid dynamic laboratory at WMU, and the laboratory was completely dark when the PIV images were taken to reduce the illumination variability. This was done by covering the backside of the Acrylic Plexiglass flume tank with black paper, covering all lab windows with black plastic sheets, and turning off the light inside the lab.

4.3.2. Analyzed images captures using the PIV technique

The wave images at three different frequencies were captured using PIV techniques, as was explained above. As was illustrated before, the main objective of this method is to obtain wave height and wavelength. Due to space limitations at the front of the wave in the test section, it was not able to increase the field of view and capture a full wavelength. Thus, Matlab code was built to create a full wavelength from many successive PIV images. The Canny edge detection algorithm technique with the constant threshold value was used to detect the edge of the wave (water surface elevation) (^{Kamanga, 2017}; ^{Lee et al., 1987}; ^{Marques, 2011}; ^{Marr & Hildreth, 1980}; ^{Shokhan, 2014}). Also, by using Matlab, the minimum points (trough) and maximum point (crest) at the one full wavelength were determined. Then, the values of wavelength and wave height were obtained by using the definition of wavelength (distance between two successive troughs) and wave height (the distance between crest and trough). Finally, to ensure that accurate results were evaluated, the final value of wavelength and wave height was calculated by taking the average of ten values obtained from ten trials, as is shown in Figure 13.

Figure 13 The procedure of water surface detection: a- Original full wavelength created b- Grayscale image c- Result from canny edge detection with constant threshold value d- Determine the maximum point (crest) and the minimum points (trough).