1. Introduction

HSLA steels are widely used in the pipeline industry (^{Xie et al., 2014}). In this sense, research continues in the direction reducing weight in vehicles and construction components, contributing to fuel reduction, and improving safety standards (^{Caballero et al., 2009}). ^{Olivares et al. (2008)} reported that steel used in the pipeline industry must fulfill stringent requirements. These necessities can be achieved by improving steel-making procedures, plate-rolling schedules, and pipe-making technologies. In this way, being feasible the production of high-grade pipes for critical applications, such as sour-service, heavy wall-pipes for deep-sea, and pipelines for arctic regions. Thus, it is noticeable that in all these applications a combination of strength, toughness, and weldability are needed (^{Takechi et al., 2003}). In this respect, from an engineering point of view, the yield strength value is one of the most important mechanical properties for pipeline design. Pipeline steel must satisfy specific yield strength values to perform its function adequately. To achieve this goal, it is essential to control the microstructure of the steel, which depends on the chemical composition and thermomechanical processing control (^{Sanz et al., 2017}).

In the present work, the results of microstructural and mechanical characterization of a Fe-0.2C-0.6Mn-0.2Mo-1.0Cr steel are reported. The studied steel was thermomechanically treated, from a soaking temperature of 1250 °C to 870 °C, and the plate cooled either in water + tempering (HR+WQ+T) or air (HR+AC). The microstructure and mechanical properties obtained from the proposed processing routes were used to quantify the different strengthening mechanism contributions to the yield strength value by using different approaches reported in literature.

2. Materials and Methods

The steel for this research was made from high purity elements Fe, Mn, Ti (99.99%) and FeSi, FeCr, FeCa, FeMo ferroalloys, placed, into an alumina crucible to avoid external contamination. Fusion started by evacuating the induction furnace’s chamber until an internal pressure of 1×10^-3 atmospheres was reached, and argon gas was immediately fed. This procedure was repeated three times, after this, melting of elements and ferroalloys was initiated. Once the bath was fully liquid, a degassing procedure was executed for 30 minutes, with the main purpose of removing any gases dissolved in the liquid melt. Then, the liquid steel was cast into a rectangular Cu-mold with the following dimensions: 3 cm thickness × 10 cm length × 5 cm width. The steel-ingot was chemically analyzed using the mass spectrophotometric technique, and the resultant chemical composition is given in Table 1.

Hot rolling of the ingot was carried out on a Fenn reversible mill (0.127 m rolls, 25 tons, and 0.166 m/s of rolling speed). The rectangular ingot had a Pt-Pt-18 % Rd thermocouple inserted at its center, and it was heated up to 1250 ºC, at a heating rate of 0.4 ºC/s, soaked for 60 minutes, and immediately hot-rolled as shown schematically in Fig. 1.

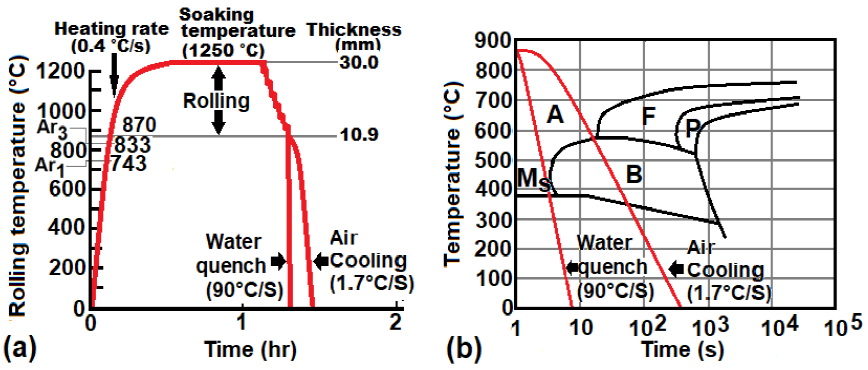
Figure 1 (a) Thermomechanical processing involving heating, soaking, rolling of slab, and cooling of the plate in different media, (b) TTT diagram (^{Vander Voort, 1991}). A=Austenite, F=ferrite, P=Pearlite, B=bainite, Ms= Martensite start temperature. 

Ingot hot rolling started at 1250 °C and ended at 870 ºC, achieving a total deformation of 63%.

After the last hot rolling pass, the plate was cooled either in stirring water with a cooling rate of 90 °C/s or in the air with a cooling rate of 1.7 °C/s. It is important to remark that the water quenched specimen was also tempered at 500 °C for 20 min as an alternative heat treatment condition.

The microstructure of the hot-rolled and cooled plates was analyzed using a scanning electron microscope (SEM, JEOL - 7600f), and a transmission electron microscope (TEM, JEOL- 1200EX), both microscopes equipped with EDS microanalysis. Samples analyzed by optical microscope (OM) and SEM were roughened to 1200 SiC sandpaper, polished with alumina, and etched with 2% Nital solution. An OM coupled to an image analyzer with a software Image Pro-Plus was used, for the quantitative determination of grain size, measuring ten fields per sample, which accounted for a total analyzed area of about 6 mm² per specimen. Thin foils for TEM were prepared using a Struers Tenupol 235 Twin Jet Electro Polisher in a 60 vol. % HNO₃ + 40 vol. % H₂O solution as the electrolyte. Finally, mechanical characterization involving tensile test measurements was evaluated according to (^{ASTM E8-04, 2004}) specifications. The specimens (n = 3) were machined with the following dimensions: 50 mm in gauge length, 12.5 mm in width, and 2 mm in thickness. Then, they were pulled to fracture at room temperature (25 °C ± 1) at a strain rate of 5.0 ×10^-3 s^-1 using an Instron 1125 machine (MTS Systems Corporation, Eden Prairie, MN, USA). One-way ANOVA analysis (Minitab 19, USA) was applied to determine significant differences between groups. p < 0.05 was accepted as statistically significant.

3. Prediction of yield strength

The approaches used for predicting the yield strength tensile property consisted of adding different strengthening mechanisms. In this sense, several mathematical equations have been reported, for instance:

^{Edmonds et al. (1990)} report:

Where σYS is the predicted yield strength value, σbase is the contribution to the yield strength value due to short-range internal stresses produced by interstitial and substitutional elements in solid solution and grain size, σdis is the contribution due to the mechanism of dislocation hardening, and σppt is the contribution due to the mechanism of precipitation hardening.

^{Yakubtsov et al. (2008)} and ^{Kozasu (1988)} proposed:

The above equations account for the contribution of short-range internal stresses produced by interstitial and substitutional elements in solid solution and grain size (σbase in Eq. 1; and σ0+σs+σss+σgb in Eq. 2). Dislocation hardening, (σdis , Eq. 1 and Eq. 2), and precipitation hardening (σdis, Eq. 1 and Eq. 2) mechanisms are also considered. Where σ0 is the Peirls-Nabarro stress, σs are the internal stresses produced by substitutional elements, σss are the internal stresses produced by interstitial elements and σgb is the strengthening due to effective grain size. The amount of σbase,σ0,σs,σss,σgb,σdis,σppt are obtained by using the following expressions:

To feed Eq. 1 (^{Charleux et al., 2001}; Honeycombe, 1997; ^{Misra et al., 2005}):

where σ0=63+23Mn+53Si+700P. On the other hand, ^{Gutierrez and Altuna (2008)} propose the following equation:

To feed Eq. 2 (^{Wang et al., 2006}):

In those expressions, the concentration of the different elements is expressed in wt. %, and the grain size (d) in millimeters(mm).

The corresponding dislocation hardening contribution is assumed to be the result of the contribution of forest dislocation. The flow stress is simply assumed to obey the classical relation with statistical store dislocation density, ρ (Honeycombe, 1997):

where α is a numerical factor that characterizes the dislocation-dislocation interaction, specific to the material, and takes a value of 0.3 for iron. M is the average Taylor factor for polycrystals corresponding to 3 for bcc-crystals. μ is the shear modulus for iron with a value of 81600 MPa, b is the Burger´s vector (=2.48×10-10 m) (^{Frost & Ashby, 1982}; ^{Nes, 1997}), and ρ is the dislocation density dislocationsm2.

The precipitation strengthening contribution is described by the Ashby-Orowan´s equation (^{Gladman, 1999}; ^{Gutierrez & Altuna, 2008}; ^{Iza-Mendia & Gutierrez, 2013}; ^{Wang et al., 2006}).

where fv is the volume fraction of the particles and x is the average precipitate diameter in microns (μm). The resultant σYS value is given in MPa.

Eq. 1 and Eq. 2 were used to predict the yield strength of polycrystalline steels which resulted from a combination of the various strengthening contributions (^{Olivares et al., 2008}), and as was presented, those equations posited a simple summation law. On the other hand, ^{Koppenaal and Kuhlmann-Wilsdorf (1964)}, ^{Majta et al. (1996)} and ^{Irvine (1976)}, employed a root mean square summation to determine the tensile property of yield strength. ^{Carretero-Olalla et al. (2014)} present the following equation:

In this sense, the present work (PW) reports the impact of the steel chemistry, coupled with the contribution of the strengthening mechanisms, which are activated by the applied hot rolling and cooling schedule, to the experimental yield strength of a developed pipeline steel grade, through quantification of the microstructural features, such as grain size, precipitation, and dislocation density; and to compare it with linearly and root square equations for the prediction of the yield strength property.

4. Results and discussions

Fig. 2a shows the microstructure obtained after hot rolling of the ingot (1250°C to 870 °C) and water cooling of the plate, from 870 °C to room temperature (and tempered at 500 °C, 20 min.), while Fig. 2b shows the microstructure of the plate hot rolled under the same experimental conditions but air-cooled.

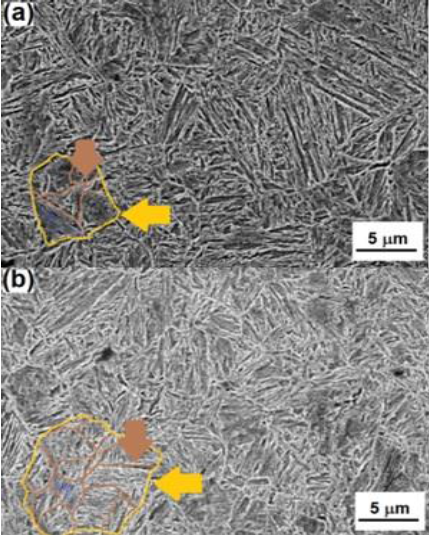
Figure 2 SEM micrographs showing microstructures of (a) HR+ WQ+ T, and (b) HR+AC. In both figures, the yellow contours are delineating packages of bainite, and the brown contours remark specimen’s grain size. 

Both microstructures are composed of bainite packages, with carbides located at the limits of bainite packages and grains, and all along the bainite phase. Grain size measurements performed on the obtained microstructures (HR+ WQ+ T and HR+AC) showed that the average packet size of the HR+ WQ+ T specimen has a value of 7.12 ± 1.22 μm with an average grain size value of 3.21 ± 0.24 μm (3.21×10^-3 mm), while the HR+AC specimen showed an average packet size 9.37 ± 1.02 μm and average grain size of 4.23 ± 0.41μm (4.23×10^-3 mm) as shown in Fig. 3.

Figure 3 Grain size measurements of the studied conditions: (a) HR+WQ+T, and (b) HR+AC. 

The resulting mechanical properties for the studied conditions presented in Table 2 and named as HR+WQ+T and HR+AC are as follows: 0.2% YS = 975.5 ± 9.7 MPa, UTS = 1047 ±10.9 MPa, ε = 35.5 ± 1.1 %, and 0.2% YS = 875.5 ± 15.2 MPa, UTS = 914.7 ± 49.0 MPa, ε = 31.5 ± 0.5 %, respectively. The results of packet size, grain size, and mechanical properties are reported as average values and the standard deviation is considered. One-way ANOVA (Minitab 19, USA) was applied to determine significant differences in groups. p < 0.005 was accepted as statistically significant.

From the chemical analysis of the steel under study (shown in Table 1), σo was obtained, and this value, together with grain size measurements, allows to calculate σbase from Eq. 4. In this way, σbase, considers the effect of the elements Cr and Mo.

The bainite microstructure obtained as a result of the two studied conditions, HR+QW+T and HR+AC, showed σbase values of 404.0 MPa and 363.3 MPa, respectively. Thus, σbase includes the effect of lattice friction and short-range internal stresses (σ0), produced by interstitial and substitutional elements in solution together with grain size (Hall-Petch relationship). For instance, Fig. 4 shows the value of σ0 for several works, including the present work (PW), where the main contribution to the value of σbase is given by the grain size, as reported by ^{Carretero-Olalla et al. (2014)} and ^{Bramfitt (1998)}. The grain size can be modified by controlling thermomechanical processing, heat treatment, or alloy composition (^{Altuna et al., 2012}; ^{Carretero-Olalla et al., 2014}; ^{Gutierrez & Altuna, 2008}; ^{Misra et al., 2005}; ^{Park et al., 2013}; ^{Sanz et al., 2017}; ^{Wang et al., 2006}). In the present work, and under the exposed experimental conditions, it was obtained a grain size of ~ 3 μm for the HR+WQ+T condition and ~ 4 μm for the HR+AC condition, contributing to 41 % to the σbase value.

Figure 4 Contribution of σ0 and grain size (k*d-12) to σbase yield strength. 

On the other hand, dislocation hardening contribution to the yield strength value was estimated, according to the classical relation with statistical store dislocation density, ρ. For this purpose, ^{Ham (1961)}, based on the work of ^{Bailey & Hirsch (1960)}, proposed a method of estimating the density of dislocations in thin foil by TEM, which consisted in measuring the total projected length, Rp, of a dislocation line for a given area, A on a micrograph, as shown in Fig. 5.

Figure 5 Bright-field TEM micrographs of the studied conditions: (a) HR+WQ+T, and (b) HR+AC, respectively. Interception points between the net and dislocations are highlighted. 

An assumption was considered for practical purposes, consisting in fixing all the dislocation segments with random orientations, concerning the plane of the film. Thus, the dislocation density is calculated according to (^{Ham, 1961}):

Where, t, is the thickness of the foil, and Rp=πNA2L (^{Bailey & Hirsch, 1960}). Then, substituting, Rp , into Eq. 9 gives:

Regarding foil thickness measurements, it was reported (^{Carretero-Olalla et al., 2014}) a thickness of 1.8×10^-7 m for Fe-0.06C-1.6Mn steel, thermomechanically treated from 1250 °C to 800 °C, followed by water cooling (dis≈320 MPa) or air cooling (dis≈155 MPa). In the present study, it was obtained a foil thickness between 1.65×10^-7 to 1.82×10^-7 m, and the derived dislocation density was between 2.29×10¹⁴ to 2.75×10¹⁴dislocationsm2, as is shown in Table 3.

The calculated contribution to the value of yield strength by dislocation hardening is 302.48 MPa and 267.07 MPa for the HR+WQ+T and HR+AC conditions, respectively. In this matter, ^{Takebayashi et al. (2010)} pointed out that investigating the mechanical properties of Fe-C steels, dislocation density, is one of the critical key factors that need to be evaluated. For instance, ^{Kehoe and Kelly (1970)}, and ^{Morito et al. (2003)} showed that the dislocation density increases with carbon content in Fe-0.01 to 0.61 wt. % C steels with ferrite or martensite microstructures, as is shown in Fig. 6, where the contribution to σdis goes from 49 MPa to 1030 MPa, depending on processing.

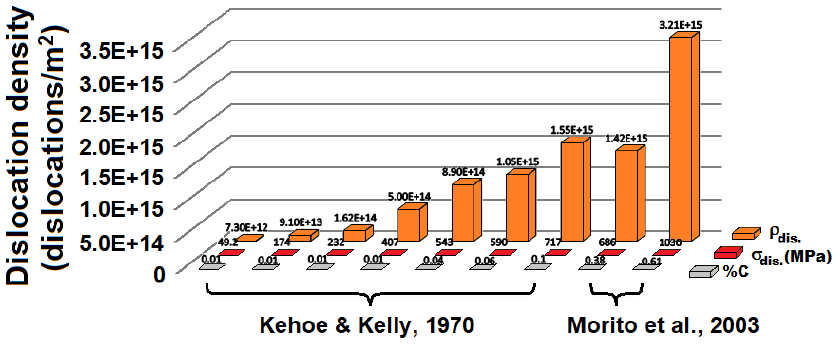
Figure 6 Contribution of dislocation density, ρdis , to dislocation hardening, σdis , as a function of carbon concentration. 

In addition, Fig. 7 shows the effect of thermomechanical processing and cooling conditions (^{Carretero-Olalla et al., 2014}; ^{Misra et al., 2005}; ^{Olivares et al., 2008}; ^{Sarkar & Jha, 2011}; ^{Takebayashi et al., 2010}; ^{Tan et al., 2014}; ^{Wang et al., 2006}), on the value of σdis , for several Fe-C plates of steel, with the addition of one or more element, such as Cr, Mn, Mo, Nb, and Ti, where the contribution of dislocation hardening takes values between 155 MPa to 320 MPa. These values are independent of its carbon content and more dependent on the processing route and cooling medium/heat treatment.

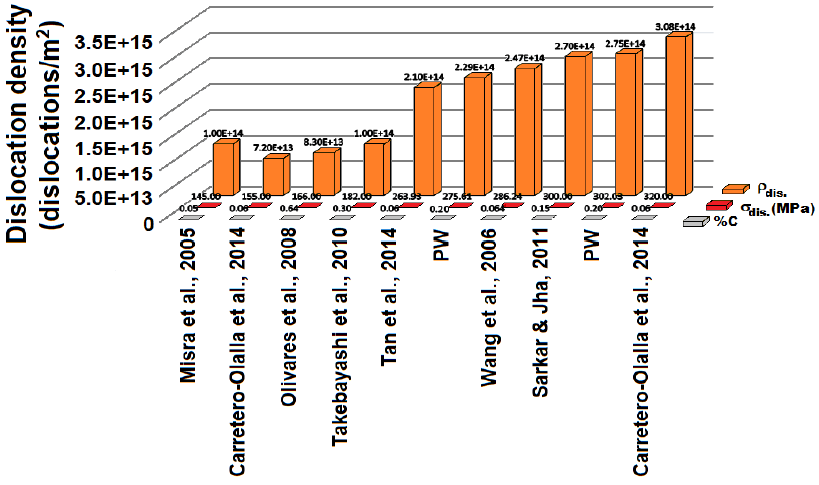
Figure 7 Contribution of dislocation density, ρdis , to dislocation hardening, σdis , as a function of carbon concentration and the effect of thermomechanical processing and cooling conditions. 

For this work, σdis , takes values from 275 MPa to 302 MPa for both studied conditions, corresponding to more than 30 % of its yield strength value (see Table 3).

In this sense, the increase of the yield strength value is also influenced by particle precipitation (carbide precipitation). Due to particles can hinder the dislocation motion increasing the yield strength, for instance, Fig. 8 shows the distribution of particle size at grain boundaries and matrix in the HR+WQ+T and HR+AC microstructures. In these micrographs, it was found a contribution to σppt from 203.93 MPa (HR+WQ+T) to 217.65 MPa (HR+AC). This precipitation strengthening effect has been reported, taken values from 73 MPa (^{Olivares et al., 2008}), 74 MPa (^{Irvine & Baker, 1984}), 94 MPa (^{Tan et al., 2014}), 203 MPa (PW), 217 MPa (PW), 272 MPa (^{Sarkar & Jha, 2011}) and 300 MPa (^{Misra et al., 2005}), depending on processing conditions.

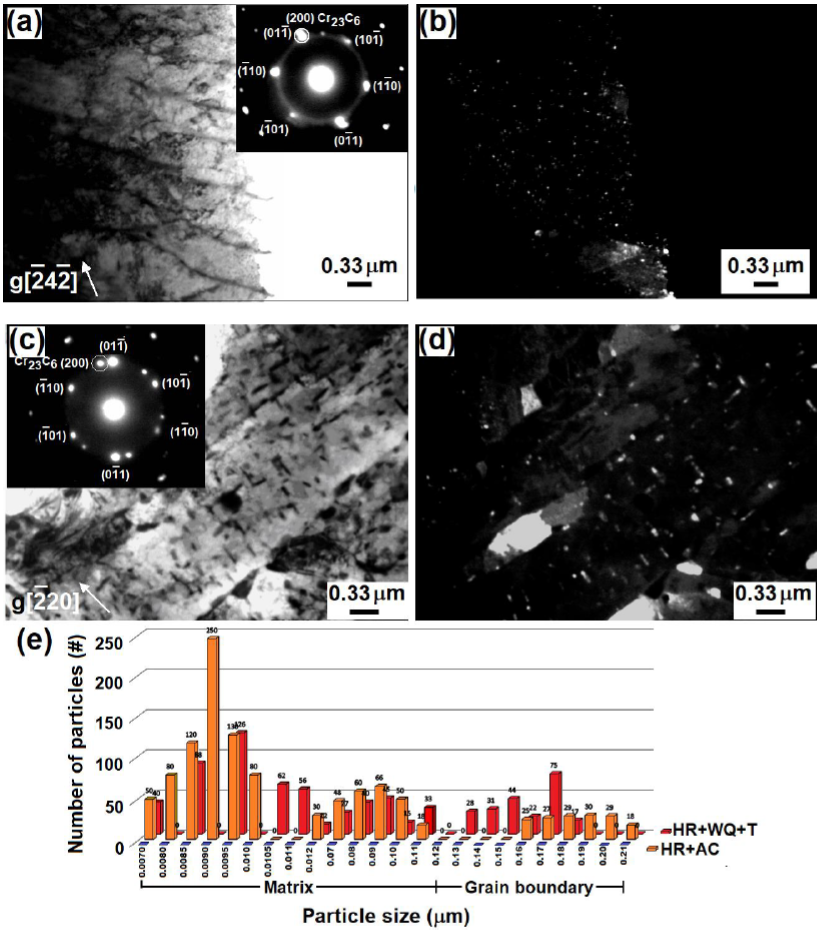
Figure 8 (a, c) TEM micrographs of the studied conditions: HR+WQ+T and HR+AC, respectively, with their corresponding electron diffraction patterns (insets); (b, d), darkfield images from selecta diffraction area where quantification of precipitates was performed, (e) distribution of particles. 

From the above results, Table 4 compares the experimental yield strength values, with predictions, for HR+WQ+T and HR+AC conditions, which were obtained, by using linearly and root square equations. It is noticeable that the contribution of short-range internal stresses produced by interstitial and substitutional elements in solid solution, grain size, dislocation hardening, and precipitation hardening was considered. Results showed that the linear equation possesses an error of up to 7.3 %, while the root square equation showed an error of up to 30 %.

As shown in Table 4, the mechanical properties obtained for this experimental steel positioned as a steel grade HSLA 120, which could have applications as high strength pipelines.

5. Conclusions

The experimental Fe-0.2%C-0.6%Mn-0.2%Mo-1.0%Cr steel was fabricated and processed putting particular attention to the yield strength value, relevant for pipeline design. According to the proposed hot-rolling schedule together with the imposed cooling-rate allowed to obtain unique microstructures with yield strength values which positioned it to an equivalent high-strength low-alloy (HSLA) steel of the HSLA-120 type. Chemical composition percentages together with a quantification of microstructural features were fed to equations to predict the contribution of different strengthening mechanisms. For example, lattice-friction and short-range internal stresses produced by interstitial and substitutional elements in solution, grain size, dislocation hardening, and precipitation hardening. In this way, it was possible to quantify a contribution of σ0 and σdis with the following values: σ0 = 41%, σdis = 31 % and σppt = 20.7 % for the HR+WQ+T condition, and σ0 = 41%, σdis = 31 % and σppt=  23.7 % for the HR+AC condition to the yield strength value. From a Hall-Petch analysis of the different strengthening contributions carried out using square summation, large discrepancies were found between the experimental and predicted values of yield strength, and much-improved correlation was quantified when using linear summation to calculate experimental yield strength values.

Conflict of interest

The authors do not have any type of conflict of interest to declare.

Financing

This work was supported by DGAPA-UNAM PAPIIT IT100119.