1. Introduction
Two fundamental problems arise in the design of control systems. Reference tracking and disturbance attenuation. It is widely known that both problems are produced by the corresponding closed-loop transfer functions (sensitivity and complementary sensitivity) (Safonov et al., 1981). While disturbance attenuation is exclusively a feedback problem, the tracking problem, which is associated with an open-loop property, can be solved by using a suitable precompensator. Therefore, the tracking problem is conveniently managed within the two-degree-of-freedom (2-DoF) control configuration. In a classical feedback control scheme, the control signal is obtained through the difference between the reference and the current output. Since there is only one input to the controller, this classical control structure is also called a one-degree-of-freedom (1-DoF) controller. Although 1-DoF controllers have many nice structural properties (Davison, 1976), a compromise must be reached to solve simultaneously the tracking and disturbance attenuation problems. On the other hand, a controller has 2-DoF, when the reference signal and the plant output can be processed independently to obtain the control signal. The advantages of using a 2-DoF control system are well known: the closed-loop properties can be configured independently of the reference tracking transfer function (Grimble, 1994). This possibility results from the separation between the response to the reference signal and the feedback transfer function.
Among the first contributions of the 2-DoF theory, it is worth mentioning (Horowitz, 1963; Vidyasagar, 1985). Since then, it can be found many published research
results on the design of 2-DoF controllers. Hoyle et
al. (1991) and Limebeer et al.
(1993) developed a 2-DoF extension of the
The problem of optimization of the 2-DoF structure has not received wide attention.
Nevertheless, some interesting works can be mentioned. The initial contributions of
Limebeer et al. (1993) and Grimble (1994), where the problem is formulated
into a general framework. The approach of Hoover et
al. (2004) which propose a simple single-input-single-output 2-DoF
pole-placement design method that provides
This paper deals with the problem of optimal design of a 2-DoF controller that will lead to zero asymptotic steady-state tracking error. The reference inputs can include steps, ramps, and other persistent signals used currently. The main idea is to translate the tracking 2-DoF problem into a state-space- feedback control synthesis one (Garcia, Tarbouriech & Turner, 2011). Where, an internal model of the reference input is introduced (Francis & Wonham, 1976). Then, through the LQR method the desired performance objectives are addressed by minimizing a quadratic cost function (Anderson & Moore, 2007; Lewis & Syrmos, 1995). Finally, the state-feedback optimal gains are linked to the polynomials used within the 2-DoF formalism. A fundamental aspect of the method is that it only utilizes the measurable information of the plant provided by its inputs and outputs.
The article is organized as follows. Section 2 considers the problem formulation. Section 3 provides the main result of the work, where it is stablished a connection between the 2-DoF system and the state-feedback control synthesis problem. Finally, Section 4 shows the effectiveness of the method by considering its application to a coupled-tank system.
Notation: Capital bold typeface letters denote matrices and small bold
typeface letters denote vectors.
2. Problem formulation
Consider a plant described by
where
with
A general 2-DoF controller (Landeau & Gianluca, 2006) can be described by
where
the controller can be thought as a combination of a feedback having the transfer
function
A block diagram of the control system is shown in Fig. 1 and an implementation of the controller that highlights the polynomials in (4) is included in Fig. 2.
The general problem under study can be formulated as follows:
Problem 1: Given the plant (1), find polynomials
In the next section, the preceding tracking problem will be solved within a state-space formulation using an optimal LQR approach.
3. Proposed method
In this section, we consider the problem of designing a 2-DoF controller that provides asymptotic tracking of a predefined reference input with zero steady-state error. The reference inputs include steps, ramps and other persistent signals currently used. The main idea is to translate the tracking 2-DoF problem into a state-space- feedback control synthesis one.
3.1. Plant and state-space model connection
Using the input - output information of the plant, it is defined the state vector
Associated with system (1), we define the following state-space system model:
the partitioned matrices
see the appendix for an example of the
connection between Equations (1) and (5). The only condition on
3.2. Controllability
For this work, it is important to assure the controllability of the equivalent state-space model.
Theorem 1: If System (1) is controllable, then System (5) is
controllable, if and only if all the roots of polynomial
Proof: A step-by-step procedure shows that the transfer function of
System (5) gives
3.3. Optimal tracking of a step reference
A fundamental result of the control theory is that zero-state tracking errors are
achieved by considering in the control policy a suitable model of the dynamic
structure of the reference signal (Francis &
Wonham, 1976). Let the tracking error
taking the derivative of (6) and using the output equation of the state-space Model (5) yields
now, taking the derivative of the state Equation (5) gives
Equations (7) and (8) can be combined as
where the augmented state vector is
to have a LQR formulation of the tracking problem, the following quadratic cost is considered
where
minimizes (10) and stabilizes System (9) with the vector
here
since, it can be easily verified that the System (9) with matrices
next, Equation (14) is developed to find the relation between the gains
the vector gain
taking the Laplace transform of the above equation yields the 2-DoF controller
defined in (3), where the polynomials
these results are summarized in the following theorem.
Theorem 2: Given the Plant (1), the control signal
3.4. Optimal tracking of a ramp reference
It is easy to show that for a ramp reference input
and the control signal is
after taking the integration two times in the control signal
the gain vector
after applying the Laplace transform to the above equation, the polynomials
the internal model principle is easily extended to other reference inputs by following the same general procedure outlined for the step and ramp inputs.
4. Results
In this section, the proposed method is applied to a coupled-tank system.
4.1. Coupled tank system
The coupled tank system is given in Fig. 3. The setup experiment also includes a 1.3 MHz Intel Pentium 4 computer and interface to LabVIEW via the data acquisition card of national instrument DAQ-USB-6008. It consists of 8 inputs and 2 analog outputs and 12 digital input/output ports. The sampling period was set to a value of 50 ms. The apparatus is used in the control laboratory at the Simón Bolívar University in Venezuela. It comprises a single pump with two tanks. Each tank is instrumented with a pressure sensor to measure the water level. The pump drives the water from the bottom basin up to the top of the system. Depending on how the outflow valves are configured, the water then flows to the top tank, bottom tank, or both. One configuration is shown in Fig. 4, where the output of the pump is connected to the first tank. The nonlinear state space model (Apkarian, 2013; Grygiel, 2016) is given in (18), here the state vector is equal to the tank’s levels, the control signal corresponds to the input voltage applied to the pump and the output is selected as the second tank level.
With
the description and numerical values of the physical parameters for the tank system are given in Table 1.
Table 1 Physical parameters of the coupled tank system.
| Description | Value | Unit |
|---|---|---|
| Pump flow constant | 4 | cm3/s/V |
| Out 1 Orifice Diameter | 0.635 | cm |
| Out 2 Orifice Diameter | 0.476 | cm |
| Tanks Diameter | 4.445 | cm |
| Tanks Height | 30 | cm |
| Gravitational constant on Earth | 981 | cm/s2 |
| Maximum flow | 100 | cm3/s |
| Pump peak voltage | 22 | V |
By employing the numerical values from Table 1. It is possible to perform the following calculations
replacing the previous values in (19) gives the linear model differential equation of the coupled tank system as
4.2. Two-degree-of freedom control system design for tracking a step reference input
Defining the state vector as
here, we have
using
Remark 1: Gain
From vector
Figure 6 exhibits the tracking ability of the 2-DoF control system structure. Three step changes are considered, and the controller always reacts satisfactorily. Figure 7 shows the pump voltage control signal, which values are always within the voltage technological limits.
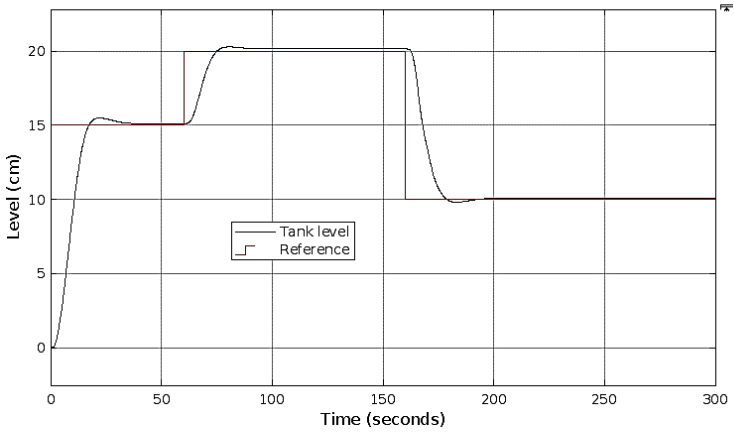
Figure 6 Second tank closed-loop liquid level response of the 2-DoF control system for the tracking problem of a step reference input.
4.3. Disturbance rejection
The disturbance attenuation of the design is now studied through the following
experiment. The system starts in the standard configuration of Fig. 2, but at
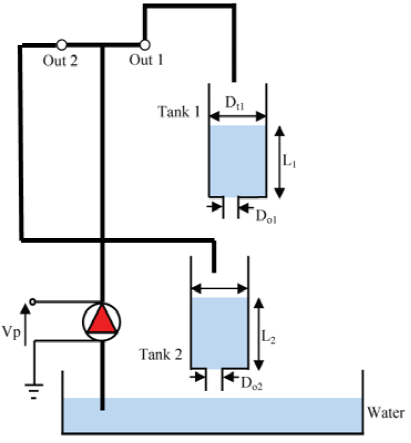
Figure 8 The connection scheme of the coupled tanks system to create a disturbance that decrease the inlet to Tank 1.
Figure 9 allows appreciating the adequate disturbance rejection achieved with the design method. At the instants of time, where the trapezoidal disturbance starts and ends, the 2-DoF controller reacts by returning the controlled output to the reference level. Figure 10 allows watching the control signal evolving within the limits of the tank pump.
4.4. Two-degree-of freedom control system design for tracking a ramp reference input
For a ramp reference input, the augmented Model (9) has matrices
using
the polynomials
The reference input applied to the coupled tank system is shown in Fig. 11, here a combination of ramps with different slopes and step changes are considering. The comparison between the reference input and the controlled output is displayed in Fig. 12, while the evolution of the control signal is found in Fig. 13.
Conclusions
In this work, it has been proposed a method to design an optimal 2-DoF control system that provides zero asymptotic steady-state tracking error to a predefined reference input. The reference inputs include steps, ramps, and other persistent signals used currently. The plant is described by an input-output model and then it is translated into an equivalent state-space model which state vector depends exclusively on the measurable information of the original system. It is established that the controllability of the state space model implies the controllability of the original system. This allows using the efficient machinery of state-feedback-controller-synthesis and then, connect the results of the state-space synthesis with the polynomials of the 2-DoF controller. The internal model principle is employed to augment the equivalent state-space model depending on the reference input considered.
Conflict of interest
The authors have no conflict of interest to declare.
Funding
The authors received no specific funding for this work.











 nueva página del texto (beta)
nueva página del texto (beta)













