3.1. Designing of PID controller

This section is focused on designing a PID as a position controller for the AMB system. The switching frequency of inner closed loop is very high as compared to the outer closed loop (^{He et al., 2020}). So, as an assumption, for designing the controller for outer loop (i.e., position controller), the inner loop is considered as unity gain. But for verification, the complete AMB system is observed with the designed controller and the impact of the inner loop on overall performance is studied.

Figure 4 AMB system with a PID controller when inner closed loop is unity. 

The PID controller transfer function K(s),

where Kp= Proportional gain, Ki= Integral gain and Kd =Derivative gain. PID controller with AMB system as shown in Figure 4 can be write in equation form by using Eq. 8 and Eq. 10, then open loop transfer function will be,

where K _x = feedback path gain or, position sensor gain. For frequency response analysis (^{Katebi, 1988}) the open loop transfer function after putting s = jω will be,

therefore,

where, x=Ki/Kp and y = K _d /K _p

at gain crossover frequency the magnitude of the open loop system is,

so,

Therefore,

by using Eq. 13, Eq. 15, Eq. 16, x and y the calculated value of Kp, Ki and Kd for closed loop AMB system at equilibrium point of operation is 4.3, 184.2 and 0.052, respectively. Therefore, Eq. 10 becomes, a PID controller is simulated using operational amplifiers, resistors and capacitors which is depicted in Figure 11. Performance of this PID controller with proposed system is observed in later section of this manuscript.

3.2. Designing of fuzzy logic controller (FLC)

Control of complex and uncertain systems was a major challenge until the introduction of fuzzy sets (^{Zadeh, 1988}) and fuzzy control. These fuzzy sets along ‘with if-and-then’ statements, create an algorithm to control complicated systems. These if-and-then statements formed using qualitative process knowledge and human-like thinking (^{Zadeh, 1990}). A block diagram representation of FLC is depicted in Figure 5.

Figure 5 Block diagram of FLC. 

Steps in designing fuzzy logic control technique are- Fuzzification, Inference and Defuzzification (^{Cox, 1992}; ^{Das & Biswas, 2021}; ^{Shieh, 2014}). Each step has its own significance which is briefly described and a two-dimensional FLC will be designed for the proposed AMB system.

A. Fuzzification

The first step after collecting all analogue data and crisp data is to transform it into the membership function of fuzzy subsets or, fuzzy sets. That it will be understandable by the inference system (^{Sain et al., 2020}). Here, triangular type membership function converts the crisp data into fuzzy sets and subsets. Figure 6 shows a triangular membership function, and its mathematical description is given by Eq. 18.

Figure 6 A triangular membership functions. 

Here μAx is the value of membership function. The inputs are in range of -l,l, where m is a point having a magnitude of ‘1’ and m lies in range of -l≤m≤l (^{Das Sharma, 2012}). The range is limited by the designer and depending upon the requirement the number of membership functions can be increased or decreased.

In this work the fuzzy controller employs two inputs: the error signal e(t) (i.e., result of comparison between reference signal r(t) and process output signal y(t)) and change in error signal de(t)dt, as shown in Figure 7.

Figure 7 Closed loop AMB system with PD-fuzzy logic controller. 

These two inputs, error signal e(t) and change in error (i.e., de(t)dt) are ranged from [-1,1] and output voltage signal ∆V(t) is ranged from [-2,2]. Each input and output are fuzzified using seven symmetrical triangular type membership functions as depicted in Figure 8 (a) and (b). Here, μex= membership function of error signal e(t), μe˙x= membership function of change in error signal de(t)dt and μVx= membership function of voltage ΔV(t).

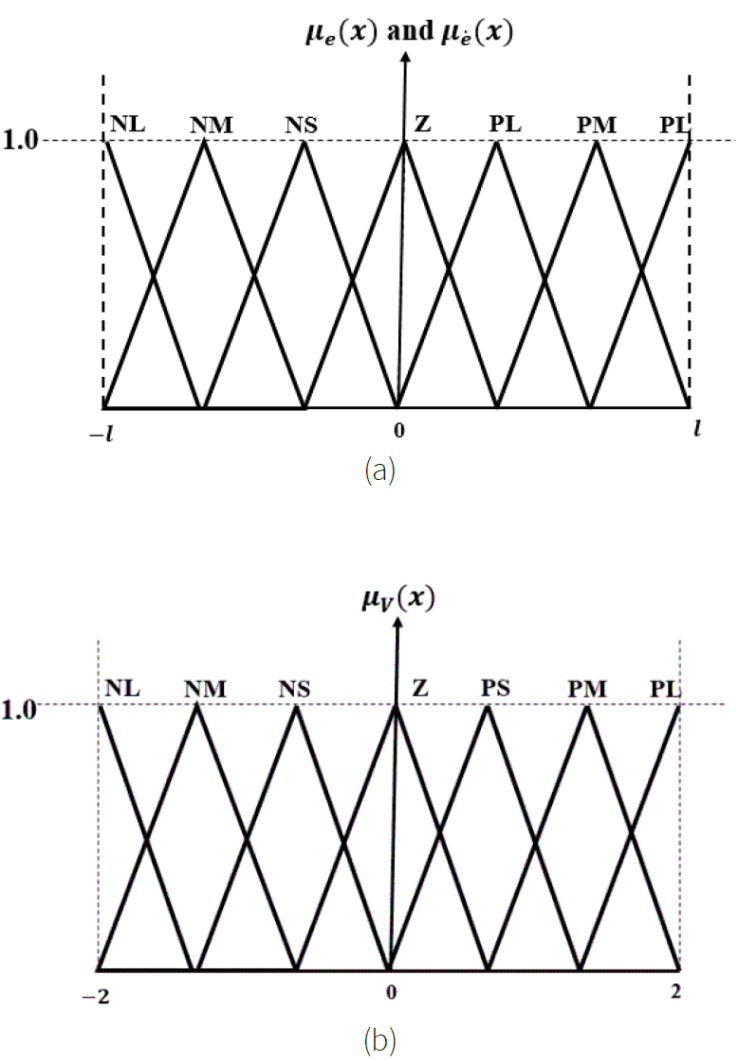
Figure 8 (a) Fuzzified inputs with seven triangular type membership function, (b) Fuzzified output with seven triangular type membership function. 

Mathematically, μe(x), μe˙x and μVx comprises of seven membership functions in their specific range (^{Agarwal & Chand, 2011}). The terms NL, NM, NS, Z, PS, PM, and PL represent negative large, negative medium, negative small, zero, positive small, positive medium, and positive large respectively. The list of fuzzified input membership functions with their range is in Table 2 and output membership functions is listed in Table 3.

Later, depending upon the rule base, operation is performed on fuzzified inputs and output in the inference engine.

B. Inference and rule base

Fuzzy inference is the process of creating a map utilizing fuzzy logic from a given input to an output. Mapping then provides a basis for judgement and trend detection. Rule base describes the mapped relation between fuzzified inputs and output. In this work, if-and-then rule is designed using two different inputs and one output, with seven membership function each, i.e., 72=49 rules relating to the inputs and output. Table 4. shows a rule base for designing FLC.

Table 4 Rule base. 

	PL	PM	PS	Z	NS	NM	NL
NL	Z	NS	NM	NL	NL	NL	NL
NM	PS	Z	NS	NM	NL	NL	NL
NS	PM	PS	Z	NS	NM	NL	NL
Z	PL	PM	PS	Z	NS	NM	NL
PS	PL	PL	PM	PS	Z	NS	NM
PM	PL	PL	PL	PM	PS	Z	NS
PL	PL	PL	PL	PL	PM	PS	Z

With reference to Table 4, all the rules can be stated in form of- “IF error is PL (positive large) AND change in error is NM (negative medium) THEN voltage is PS (positive small)”. In terms of membership functions, it can be rewritten as- “IF error is μePLx   AND change in error μe˙NMx THEN voltage is μVPS(x)”.

Similarly, all the 49 rules are created in rule base editor of fuzzy tool of MATLAB. Depending upon these rules the inference engine executes the process and generates output accordingly (^{Li & Gatland, 1996}). The output is further defuzzified (i.e., conversion of fuzzified data into raw data or crisp data) to make the output data understandable.

C. Defuzzification

There are more than seven methods are available for defuzzification purpose. All have their significances and advantages. But among them the most useful method is centroid method or, center of area method (^{Mohan & Sinha, 2008}). Based on the center of gravity of the fuzzy set, this technique delivers an exact value. It can be defined by the algebraic expression, (Eq. 19). Pictorial representation of centroid method of defuzzification is shown in Figure 9.

where, x ^*= defuzzified value of x

Figure 9 Centroid method of defuzzification. 

3.2.1. Designing of proportional integral derivative-fuzzy logic controller (PID-FLC)

The designed FLC, shown in Figure 7 is a PD-FLC which can be modified to perform as a PID -FLC (^{Arun & Mohan 2018}; ^{Lai & Lin, 2003}). Implementing an integrator to the output of PD-FLC and taking a summation of output of the integrator with output of PD-FLC becomes a PID-FLC (^{Li, 1997}) as shown in Figure 10.

Figure 10 A simplified PID-Fuzzy logic controller (PID-FLC). 

The designed PID-FLC is used as a position controller for the proposed AMB system, its performance is observed and compared with PD-FLC and PID controller. In the next section, different controllers will be simulated with the proposed AMB system, and their effect and performance are observed.

4.1. Simulation of proposed active magnetic bearing (AMB) system with PID controller

For different parts of PID controller resistor and capacitor values are calculated as:

For proportional part of PID controller when K _p =4.3,

let, Rin=1KΩ

for integral part of PID controller when K _i =184.2,

let, C _i = 1 x 10^-6 F

for derivative part of PID controller when K _d =0.052,

let, C _i1 = 1 x 10^-6 F

using these values of Rp, Rin, Ri, Ci,Ri1 and Ci1 a PID controller is simulated as shown in Figure 11. and a pulse of unit step is applied to it to observe output of each part of PID controller.

Figure 11 PID controller using analog electronics components is designed in Simulink MATLAB. 

Figure 12 shows the input, which is a pulse of unit step signal for three cycles and output of each part of PID controller. (i.e., proportional, integral, and derivative respectively).

Figure 12 Output of different parts of PID controller for a pulse of unit step input signal. 

In this study, transfer function (Eq. 9) is used for all observation and computation. With reference to Figure 4, when the inner closed loop is set to unity, the proposed AMB system is simulated with a PID controller, as illustrated in Figure 13.

Figure 13 Proposed AMB system (when inner closed loop is unity) with PID controller. 

A unit step signal is provided as input to the system, allowing observers to examine how the closed loop performs in transient state.

Observed transient state parameters are listed in Table 8, where percentage overshoot is 18.452% which is in a stable region at the peak time is 0.066 sec, rise time is 0.02468 sec and settling time is 0.14287 sec. Calculated damping ratio (ξ)= 0.47268, which is in between control design limit that is 0< ξ <1.

Next, the complete proposed AMB system, as depicted in Figure 2, is simulated. Here, the current controller is a Proportional-Integral (PI) (^{He et al., 2020}), and a single switch power amplifier (^{Debnath et al., 2020}) is intimated for the inner closed loop. The designed PID controller is implemented as a position controller. The simulation layout of the complete AMB system is shown in Figure 14, and for a unit step signal, step response has been plotted and transient state parameters have been observed which are listed in Table 8.

Figure 14 Complete AMB system with PID controller. 

Transient response of complete proposed AMB system is studied which has a peak overshoot of 22.84% at a peak time of 0.070 sec, rise time is 0.02637 sec, settling time is 0.14164 sec and calculated damping ratio (ξ) = 0.4253.

To compare the transient state performances of both forms of the closed loop with the designed PID controller, step responses are plotted on an X-Y axis as shown in Figure 15. It is evident from the step plots of Figure 15 that the designed PID controller when implemented with the complete proposed AMB system shows a rise in overshoot, rise time and peak time. This change in transient state parameters (which is listed in Table 5) is due to the presence of an inner closed loop. Although, the designed PID controller is still able to maintain the system in underdamped region (0 < ξ < 1).

Figure 15 Step responses with PID controller. 

Using the designed PID controller with complete proposed AMB system the percentage overshot increased by 23.78% and damping ratio reduced by 10%. There is a little decrement in the settling time which means that the complete proposed AMB system with PID controller settles fast as compared to proposed AMB system with PID controller (when inner closed loop is unity).

4.2. Simulation of proposed active magnetic bearing (AMB) system with PD-FLC

Fuzzy logic controller (FLC) is designed for the proposed system using fuzzy toolbox application of MATLAB (^{The MathWorks, 1998}). For creating a fuzzy rule base, the first crisp data input and output has been defined in a form of membership function as shown in Figure 16 (a) and (b). Later this fuzzified data is processed to an inference engine and depending upon the designed rules output is generated which is defuzzified into crisp data form.

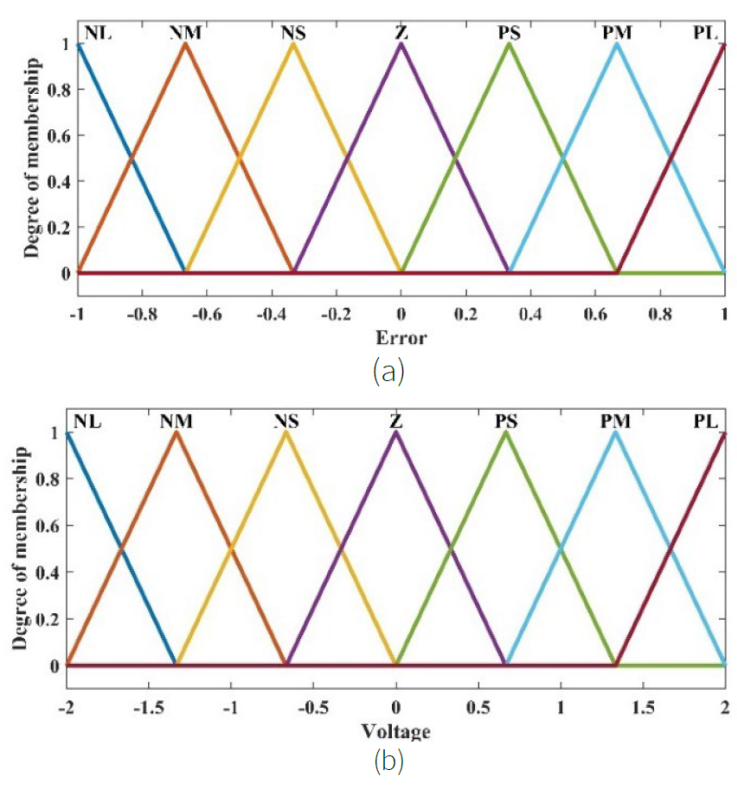
Figure 16 (a) Fuzzified inputs and (b) Fuzzified output with seven triangular type membership function. 

In this paper, fuzzy inference system (FIS) is of Mamdani type (^{Aceves-López & Aguilar-Martin, 2006}) and rule base editor creates all of the 49 rules which has been described in subsection 3.2. A three-dimensional plot of rule base is shown in Figure 17 where on X-axis error signal is labelled, change in error signal is labelled on Y-axis and output is laid out on Z-axis, to their respective range.

Figure 17 Three-dimensional plot of fuzzy rules. 

As illustrated in Figure 18, the created fuzzy logic controller is also employed as a position controller with the proposed AMB system.

Figure 18 Proposed AMB system (when inner closed loop is unity) with PD-FLC. 

When PD-FLC is a position controller for the proposed AMB system (when inner closed loop is unity) shows a peak overshoot of 8.152% which is 10.3 unit less than PID controlled. With the implementation of PD-FLC as a position controller, rise time, peak time and settling time of the closed loop reduce to 19.327%, 30.30% and 34.457% respectively (compared to PID controller).

Referring to Figure 2, the complete proposed AMB system is simulated in MATLAB with PD-FLC as a position controller as shown in Figure 19.

Figure 19 Complete proposed AMB system with PD-Fuzzy logic controller (PD-FLC). 

Comparing the data obtained for PD-FLC with complete proposed AMB system, with PID controller, shows a reduction of 58.96% in peak overshoot with a value of 14.368%, other than this peak time, rise time and settling time also get reduced by 42.85%, 36.67% and 27.32% respectively.

Due to the inner closed loop, the peak overshoot value for complete proposed AMB system with PD-FLC has increased but it is still 37.09% less than PID controller with complete proposed AMB system. The increment and decrement of various transient state parameters values of proposed AMB system (when inner closed loop is unity) and complete proposed AMB system with PD-FLC is listed in Table 6. Step responses for both forms of closed loop proposed AMB system is shown in Figure 20.

Figure 20 Step response with PD-FLC. 

Reduction in rise time and peak time lead to a faster response but increased settling time make the complete system sluggish in steady state region but compared to PID controller with complete proposed AMB system, the performance is improved. Further improvement in transient state parameters can be observed with the implementation of PID-FLC as a position controller for the proposed system.

4.3. Simulation of proposed active magnetic bearing (AMB) system with PID-fuzzy logic controller (PID-FLC)

PID-FLC as a position controller for the proposed AMB system (when inner closed loop is unity) is simulated in MATLAB as illustrated in Figure 21 and unit step signal is input to observe the step response of the closed loop.

Figure 21 Proposed AMB system (when inner closed loop is unity) with PID-FLC. 

Transient state parameters obtained by the step response of PID-FLC with proposed AMB system (when inner closed loop is unity) shows a decrement in peak overshoot. As compared to PID controller and PD-FLC, the peak overshot reduced by 62.12% and 14.266% respectively. Remaining other parameters like rise time, peak time and settling time also get reduced and their values are listed in Table 8, which makes the closed loop faster with less oscillations. The same PID-FLC is simulated with the complete proposed AMB system by applying a unit step signal as a reference signal which is shown in Figure 22.

Figure 22 Complete proposed AMB system with PD-Fuzzy logic controller (PD-FLC). 

The step response of complete proposed AMB system and proposed AMB system (when inner closed loop is unity) with PID-FLC is plotted in Figure 23 and changed data is shown in Table 7.

Figure 23 Step response with PID-FLC. 

The information in Table 8 makes it clear that the proposed AMB system with PID-peak FLC has an overshoot value of 11.798%. It is still the minimum obtained overshot as compared by PID controller and PD-FLC with complete proposed AMB system.

It is noticeable from Table 8 that implementing the PID-FLC on the complete proposed AMB system improves the overall response of the system.

Next section will show comparison among performance of PID, PD-FLC and PID-FLC, as a position controller. First, with the proposed AMB system (when inner closed loop is unity) and then with the complete proposed AMB system.

4.4. Performance comparison among PID controller, PD-FLC and PID-FLC

For the proposed AMB system when inner closed loop is unity, the step responses with different controllers are shown in Figure 24 and data of the transient state parameters are listed in Table 8. Comparing the transient parameters values of PID controller with PID-FLC clears that the peak overshoot, rise time, peak time and settling time are improved by 62.12%, 32.21%, 40.90% and 58.88% respectively. This improvement makes the closed loop faster and more robust to sudden changes.

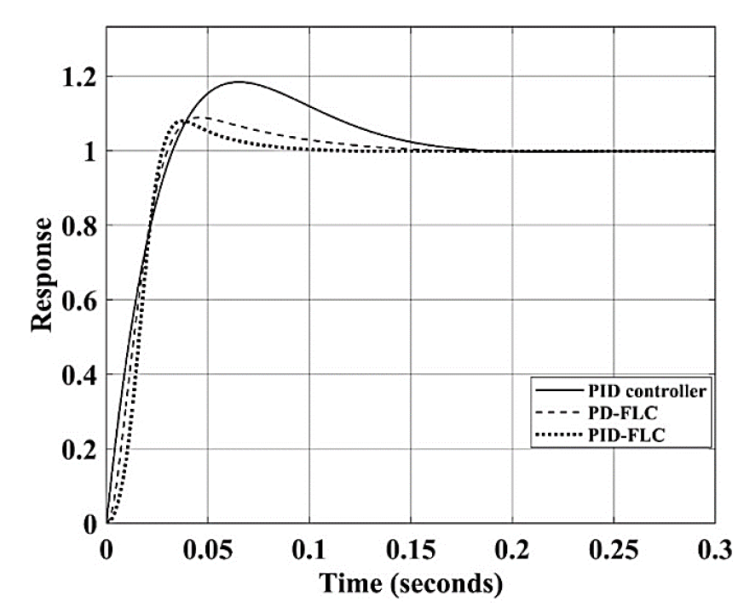
Figure 24 Step responses of proposed AMB system (when inner closed loop is unity) with PID controller, PD-FLC and PID-FLC. 

For second-order systems, the closed-loop damping ratio is (^{Nise, 2011}),

Therefore, when inner closed loop is unity the Phase margin with PID controller ≅ 100 × 0.47268 = 47.26°, with PD-FLC ≅ 100 × 0.62372 = 62.372° and with PID-FLC ≅ 100 × 0.64630 = 64.630°.

Phase margin of a system shows allowable open loop phase change to a system to make its closed loop unstable. This margin should be so appropriate and precise as higher value of phase margin leads to a sluggish performance and lower value will show a little stability margin. With PID-FLC the phase margin of the system increased by 36.73% over PID which results in an increased stability region.

From Figure 24 it is noticeable that the PID-FLC gives a smooth and better transient performance as compared to PID and PD-FLC.

The step responses of different controllers with the complete proposed AMB system are depicted in Figure 25 and the related transient state parameters are shown in Table 8. Here, again the PID-FLC shows an improvement in performance over PID and PD-FLC and comparison between PID and PID-FLC explains that peak overshoot, rise time, peak time and settling time reduced by 48.345%, 41.52%, 50% and 49.18% respectively.

Figure 25 Step responses of complete proposed AMB system with PID controller, PD-FLC and PID-FLC. 

The phase margin of the complete proposed system with PID controller is 42.53°, with PD-FLC is 52.54° and with PID-FLC is 56.24°. The increased phase margin with PID-FLC (13.71° as compared to PID, almost 32.23% increment) represents that the complete proposed AMB system with PID-FLC is more stable as compared to PID and PD-FLC. Range of the dynamic parameters obtained from the analysis are listed in Table 9 below.

From Figure 24 it is noticeable that the PID-FLC gives a smooth and better transient performance as compared to PID and PD-FLC

The step responses of different controllers with the complete proposed AMB system are depicted in Figure 25 and the related transient state parameters are shown in Table 8. Here, again the PID-FLC shows an improvement in performance over PID and PD-FLC and comparison between PID and PID-FLC explains that peak overshoot, rise time, peak time and settling time reduced by 48.345%, 41.52%, 50% and 49.18% respectively.

The phase margin of the complete proposed system with PID controller is 42.53°, with PD-FLC is 52.54° and with PID-FLC is 56.24°. The increased phase margin with PID-FLC (13.71° as compared to PID, almost 32.23% increment) represents that the complete proposed AMB system with PID-FLC is more stable as compared to PID and PD-FLC. Range of the dynamic parameters obtained from the analysis are listed in Table 9 below.

Here, from the Table 9, it is easily observable that the phase margin for the overall system varies from 40⁰ to 65⁰. This range is most desirable as the system shows better stability and a speedy performance in between this range.

4.5. Comparative analysis

Peak overshoot is shown in the Table 10 above as %MP. Different academics have suggested a variety of controlling approaches for distinct structures and models of AMB system. It can be seen from Table 10, that there is a larger overshoot when using traditional controls like lead and PID. As modern or intelligent controllers like fuzzy, optimization techniques and FO-PID are implemented, the overall system performance gets improved. The minimum overshoot recorded with traditional controllers is 14% (nearly), while the minimum overshoot observed with fractional order-PID is 11%.

This overshoot is further enhanced with its related time domain parameters using fuzzy-PID controller. For the case when inner current controlling loop is unity, the fuzzy-PID controller shows a peak overshot of 6.989%. Considering the completely proposed loop of AMB system the obtained peak overshoot further reduces to 11.798%.