1. Introduction
The use of solar energy is becoming more and more popular as an efficient substitute for conventional energy sources. Solar photovoltaic (PV) technologies are widely recognized worldwide for their environmental and sustainable nature and their diverse potential uses in industrial and residential applications (Iysaouy, Idrissi, et al., 2019). The PV energy systems extend well from small-scale power generation in autonomous systems to larger-scale energy generation like photovoltaic energy farms (Lahcen et al., 2018; Pareek & Dahiya, 2015; Rani et al., 2013). Therefore, partial shading is considered key behind the depreciation of the PV system performance in terms of efficiency, lifespan, and outlet power (Balato et al., 2011; Sundareswaran et al., 2015). There are two categories of partial shading sources: predictable and unpredictable. The first is caused by the adjacent buildings, trees, and shadows of the modules, which can be carefully managed during installing the PV systems. The second one is attributed to clouds, snow, temperature, aging effect, dust, bird spots, etc. (Higuchi & Babasaki, 2018; Jha & Triar, 2019; Karatepe et al., 2007; Lahcen et al., 2018; Manganiello et al., 2015; Pareek & Dahiya, 2016; dos Santos Vicente et al., 2020). Several approaches to decrease partial shading effects: system structures, maximum power point tracking MPPTs techniques, converters, inverter, and micro-inverter topologies and PV array configurations (Huynh et al., 2013; Marhraoui et al., 2018; Sundareswaran et al., 2015). The PV array is considered among the most suitable approaches to reduce power losses.
The partial shading produces power losses that depend on the shading patterns, the position of the shaded module in the array, and the configuration of the matrix.
Various array configurations in the literature such as series-parallel (SP), bridge linked (BL) and honeycomb (HC), total cross tied (TCT), are compared for their losses, shunt resistance effect, maximum power, diode derivation, and for different array sizes under partial shading (Lahcen et al., 2018; Pachauri et al., 2018; Pendem & Mikkili, 2018; Rani et al., 2013). According to (Gautam & Kaushika, 2002), the use of TCT can improve the life of a PV array. The analysis discussed by Kaushika and Gautam (2003) shows that the TCT configuration is the most appropriate solution to decrease the problem of mismatches under partial shade. However, () this conclusion was pinned by the results presented by the Sudoku rearrangement scheme introduced by Rani et al. (2013).
The introduced topology displays an improvement of power production by 3.6% compared to the TCT configuration. This Sudoku configuration is based on the modification of the physical location of the PV array. Further, a matrix of PV modules size (9×9) is associated in an array arranged based on the Soduku puzzle to spread the effect of shadow over the whole PV array. As an extension of the Sudoku method, the authors in Potnuru et al. (2015) elaborated an optimal Sudoku configuration to overcome the effect of shadow and to use such an interconnection that is worked for a larger PV array dimension of (36×36) seen as a (4×4) or a (9×9) sub-blocks.
The unsubstantiated aspect and unique characteristics of the Sudoku pattern for a specific array size complicate its choice because each pattern results in a different shade distribution as well as a different energy yield(field). Also, the wiring gets trickier as the size of the array increases, as the panels are not consistently relocated. These limitations have led to the development of other reconfiguration schemes based on puzzle models such as the magic square (MS), new zig-zag technique, cross diagonal view (CDV), competence square (CS), magic square view (MSV) (Dhanalakshmi & Rajasekar, 2018; Iysaouy, Lahbabi, et al., 2019; John Bosco & Carolin Mabel, 2017; Vijayalekshmy et al., 2016a).
Yadav et al. (2016) are widely reported the performances (power loss, fill factor, and shading dispersion effect on maximum power point (MPP) of the following PV array configuration: series-parallel (SP), total-cross-tied (TCT), bridge-linked (BL), honey-comb (HC) and proposed hybrid SP-TCT, BL-TCT and non-symmetrical puzzle patterns based configurations such as NS-1 (non-symmetrical-1) and NS-2 (non-symmetrical-2)
(Vijayalekshmy et al., 2016a, 2016a) are investigating a new zig-zag technique for altering and changing the interconnections of photovoltaic panels in the TCT configuration. The power loss, mismatch loss, power enhancement, fill factor, performance ratio, and irradiation mismatch index of this new zig-zag technique has been compared for classical TCT, OTCT, and NTCT schemes. It is found that this topology presented an equal improved performance with optimal total cross tied configuration.
In another work, Yadav et al. (2017) are comprehensively reported the performance (current and power at global maximum power point GMPP, power losses, and FF) of 4 × 4 PV array configurations, for instance, TCT, hybrid SP-TCT, BL-TCT, BL-HC, and rearranged configurations framing a novel configuration RTCT, RSP-TCT, RBL-TCT, RBL-HC based on MS puzzle using MATLAB/Simulink. It is found that MS-based reconfigurations arrangements such as RTCT, RSP-TCT, RBL-TCT, and RBL-HC with puzzle shade dispersion improve the performance as compared to the TCT, SP-TCT, BL-TCT, and BL-HC PV array configurations for most scenarios of partial shading.
John Bosco and Carolin Mabel (2017) are introduced a novel configuration called a cross diagonal view (CDV) arrangement to alter the location of PV modules and to improve the PV power generation under partial shading conditions (PSC). It is found that CDV configuration exhibits a high performance under different shading patterns compared to SP, TCT, and SDK.
Dhanalakshmi and Rajasekar (2018), proposed a new technique named competence square (CS) for the PV generating systems. This competence square is devised a onetime relocation technique that follows a unique number pattern to readjust the placement of the PV modules. The investigation result of the performance (the output power, fill factor, power losses) of this technique under different shading scenarios elucidate the effectiveness of this method in spreading the partial shading over the entire PV array compared to the TCT.
In all the works cited above, the configuration of PV giving the best performances under partial shading conditions is strongly desired and arouses great interest among the research community. Our previous work (Iysaouy, Lahbabi, et al., 2019) proposed a new MSV based method of dispersion of the shading on the photovoltaic array. The results we obtained for long-wide shading are better compared to those of TCT and SuDoKu configurations. Here, in this work, we propose to extend this new MSV method to other types of shading patterns in order to generalize this method. Indeed, we are going to study four typical shade cases, which are short and wide (SW), long and wide (LW), long and narrow (LN), and short and narrow (SN). However, we limit performances in comparison to the TCT and recently proven methods from literature such as competence square (CS) method (Dhanalakshmi & Rajasekar, 2018).
The improvement in the performances (performance) of the output power of MSV compared to the TCT is shown by the simulation of their (P-V) characteristics which are performed under MATLAB / Simulink for different PSCs by using a matrix of PV modules of size (9× 9). The performances of these configurations are analyzed in terms of maximum power delivered, will then be compared with some results from the literature. This will be one of the main ways to confirm that the MSV configuration offers good performance under PSCs. This is because the MSV configuration increases the dispersion of the shading effect over the entire PV system.
2. Materials and methods
In this paper, a two-diode model (Ishaque et al., 2011; Lahcen et al., 2018) is used to model the PV cell, considering recombination phenomena and providing more precision for the electrical characteristics I-V and P-V. Compared to the single diode model, this model is more complex and more accurate. The two-diode model circuit of a solar photovoltaic cell is modeled as a shunted current source with a two-diode considering two resistors: the parallel resistance and the series resistance. A photovoltaic module consists of several solar photovoltaic cells associated in series to provide the required voltage and represented by the equivalent circuit (Iysaouy, Lahbabi, et al., 2019; Lahcen et al., 2018) exposed in Figure 1. The current generated is related to the voltage of a PV module to an irradiation G by the following Equation (Ishaque et al., 2011; Lahcen et al., 2018):
Where:
q: |
The charge of the electron in coulom, |
K: |
Boltzmann’s constant in Joule per Kelvin, |
T: |
The temperature in kelvin, |
Tref: |
The temperature in kelvin, |
V: |
The voltage of the PV cell, |
I: |
The current delivered by the photocell in amperes, |
Iph: |
The photo-current in amperes, |
Is1: |
The saturation current of D1 in amperes, |
Is2: |
The saturation current of D2 in amperes, |
α 1: |
The non-ideality factor of D1 the junction, |
α 2: |
The nonideality factor of D2 the junction, |
Rs: |
The series resistance, in Ω, |
Rsh: |
The shunt resistance, in Ω. |
Ns: |
The number of cells in series. |
Np: |
The number of cells in parallel. |
3. Modelling of PV configurations under partial shading conditions
For the simulation of the TCT and MSV configurations, we used a matrix of (9×9) PV array configurations. 81 PV modules are employed. An antiparallel bypass diode shields all PV modules and strings. These PV panels are operated at a steady temperature of 25°C and at different irradiation levels. The characteristics of the PV module are given in Table 1.
4. Modelling of conventional solar PV interconnection schemes
The interconnection scheme refers to the configuration of the interconnecting photovoltaic panels in an array to produce greater output power. The researcher has investigated several techniques of multiple configurations to interconnect the photovoltaic panels. The most common conventional approaches are the SP, BL, TCT (Lahcen et al., 2018; Pendem & Mikkili, 2018; Rani et al., 2013). These configurations generally require shorter wiring than shade distribution techniques; hence, their cable losses and costs are much lower. Besides, these schemes can be applied to all array dimensions. Nevertheless, they cannot spread the shade over the array; therefore, PSCs can significantly decrease their performance. Moreover, they have a greater number of maximum power points (MPPs), making the maximum power point tracking process (MPPT) more complicated tasks resulting in a reduction in performance.
4.1. Total cross tied (TCT) configuration
Figure 2 illustrates a TCT configuration that connects all the columns of a PV array in series and rows in parallel. Therefore, it is considered as the scheme that demands the highest number of wires. In this scheme, the effects of PSCs are low because the interconnection between the PV strings balances the impact of the non-uniform illustration level on each of the links in TCT (Iysaouy, Lahbabi, et al., 2019; Kumar et al., 2016; Lahcen et al., 2018; Rani et al., 2013). Besides, in most configurations with more interconnects, they rarely could activate the bypass diode. As a result, they minimize mismatches losses, those caused by hot spots and multi-peak impacts.
The voltage and output current relationships of a TCT configuration are like those of the SP interconnect scheme, calculated in Rani et al. (2013). In this configuration, the sum of the module currents is along any row is the array current, and the sum of the module voltages along any column is the same as across the array (Iysaouy, Lahbabi, et al., 2019; Kumar et al., 2016; Lahcen et al., 2018).
5. Shade distributing techniques
The main objective of shade distribution techniques would be to reach a higher efficiency than conventional approaches under PSCs (Iysaouy, Lahbabi, et al., 2019; Vijayalekshmy et al., 2016b). Moreover, due to their ability and power to disperse the shades over the entire network, the ability to turn on the bypass diode is somewhat limited, which results in energy can be enhanced by utilizing a shade distribution technique while reducing the number of local peaks (LPs).
With a significant reduction in the number of local peaks in the electrical characteristics P-V of the system, the MPPT became a more straightforward task and led to a more efficient and less complex system. Figure 3 highlights the concept behind shade distribution techniques and the benefits of their implementation. The used techniques are Sudoku, MS. However, we focused just on MSV configuration.
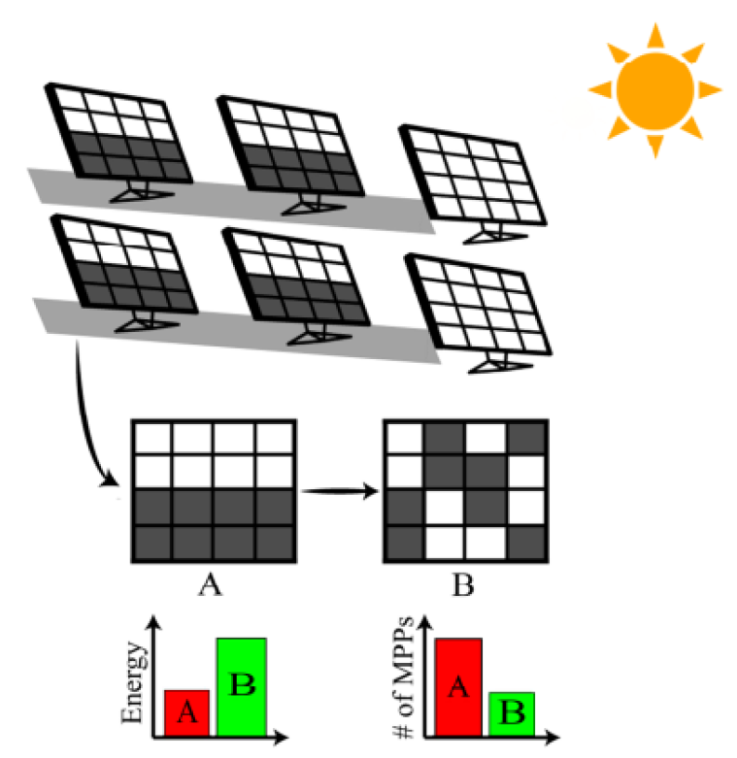
Figure 3 Partial shading effect on several panels in an array resulting in a lower power generation.
5.1. Magic square view (MSV) configuration
In our previous work (Iysaouy, Lahbabi, et al., 2019), a new method of shade distribution called the magic square view is proposed. In this method, we consider a (j ×j) PV module matrix, where j represents the number of rows and columns and must be odd j = (2i + 1) with i is an integer between 1 and n2 in a linked array (j × j) TCT. This method consists of a rearrangement of the PV panels of the array in such a way that the total of the entries of any row, column, or diagonal remains equal. An example of this arrangement of PV panels in MSV configuration for a (9 × 9) network is illustrated in Figure 4 (b). In this example, we place the integer 1 in the middle of the 9th column, then place the number of the next panel 2 in the lower right part of the present module. If this position is already occupied by another panel, the next panel must be placed immediately to the left of this module. It can be noted that this approach is based on a " wraparound " array. Thus, if a PV panel is displaced off on one side of the PV panel, it re-enters the opposite (Iysaouy, Lahbabi, et al., 2019). By increasing the incoming current to a specific node, thereby minimizing the bypass of the panels.
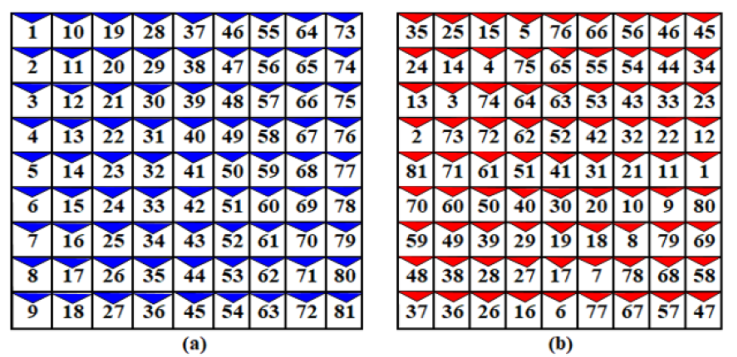
Figure 4 Magic square view shade distribution method for a 9 × 9 PV array, (a) TCT non-reconfigured array, and (b) TCT reconfigured array.
For the PV modules, their physical locations are moved without altering their electrical connections of the PV module, as in the case of the Sudoku configuration (Rani et al., 2013). Thus, this approach decreases the shading between modules in the same row and extends the impact of the shading disperses it over the entire array. In this way, the MSV configuration enhances the current flowing through a node during partially shading conditions and therefore reduces power dissipation.
6. Description of partial shading conditions on PV array configurations
The effect of shading on a PV array depends on the number of shaded modules per column and per row. In general, four types of partial shading are studied: SW, SN, LW, and LN. These four types are presented and exposed to constant irradiation levels on each PV module. The description of this partial shading condition and each level of solar irradiation on PV arrays (9 x 9) is given as follows.
6.1. Short and wide shading condition
When shading covers five of nine strings in the PV configuration, and the number of shaded panels per string is four, this pattern is attributed to a SW shading case. This case of shading in the TCT configuration is shown in Figure 5 (a). Further, Figure 5 (b) presents the conventional arrangement in which the magic square method is applied. It is apparent from these figures how the shaded modules are dispersed throughout the system.
To evaluate the performance of the PV array under partial shading conditions, the PV array is exposed to four distinct levels of irradiation:
The first group of PV array receives a level of 900W/m2. The second group was subjected to an irradiation level of 600W/m2. The third and fourth groups were exposed to an irradiation of 400W/m2 and 200W/m2, respectively. This shading pattern is shown in Figure 5. The row currents should be intended to find out the position of the Global Peak GP. The maximum output current from (Lahcen et al., 2018; Rani et al., 2013) a row for each module is equal to the total of the current limits of each module. For the first row, the current limit is determined as follows:
Where k ij = G ij = G0, G ij is the actual irradiance of the PV module, G 0 is the standard PV module at 1000 W/m2 and the coefficients, and i and j represent the row and string index, respectively. To facilitate calculations, we can assume that all PV modules are in the same state; therefore, we can write:
For the SW pattern presented in Figure 5, the PV modules in rows 1 to 5 were exposed to the same irradiation (900W/m2). Therefore, the maximum current generated for the first five rows is determined as:
Where Im is the current of the PV module at standard conditions.
In row 6, the six PV modules are exposed to radiance level 600W/m2 and the four next modules are exposed to 900W/m2. The maximum current produced is calculated in the same way and is as given by Eq. (6). The same calculation principle of the courant is used for the following rows.
The same calculation principle of the courant is used for the following rows.
The maximum current generated by rows varies following the received irradiation.
The maximum current generated by rows varies following the received irradiation.
Since the voltage variations of each row are very small, the PV arrays voltage is expressed as
Va = 9Vm,
- where Vm is the voltage produced by the module at standard conditions.
- if no modules are bypassed. Moreover,
Va = 8Vm + Vd, if a single row is bypassed,
Vd corresponds to the voltage through the diode.
Since Vd ≺≺ Va; Va can be ignored.
The power generated by the array is:
Where Im is the current generated by the module at standard irradiance 1000 W/m2.
6.2. Long and wide shading condition
This case of shading in the TCT configuration is shown in Figure 6 (a). Further, Figure 6 (b) presents the conventional arrangement in which the magic square method is applied.
According to this shading pattern, a photovoltaic array is divided into five distinct clusters by irradiation levels. Group 1 is exposed to 900 W/m2 irradiation, whereas the rest of the group receives 600 W/m2, 500 W/m2, 400 W/m2, and 200 W/m2, respectively. This shadow pattern is depicted in Figure 6. Since all columns and many rows are shaded, this corresponds to the case of LW shading (Lahcen et al., 2018; Rani et al., 2013). We have studied this case only to compare it with the literature.
6.3. Long and narrow shading condition
This is so-called as only some columns are partially shaded and could appear as a group anywhere in the array. This case of shading in the TCT configuration is shown in Figure 7 (a). Further, Figure 7 (b) presents the conventional arrangement in which the magic square method is applied. According to this shading pattern, a photovoltaic array is divided into four distinct clusters by irradiation levels. In this case, the array is exposed to four irradiation levels which are 900 W/m2, 700 W/m2, 400 W/m2, and 300 W/m2, respectively.
6.4. Short and narrow shading condition
The irradiation levels used in this case are 900 W/m2, 600 W/m2, and 400 W/m2, as shown in Figure 8 (a). Moreover, Figure 8 (b) presents the conventional arrangement in which the magic square method is applied. In contrast to the previous cases, because a very small group of panels is subject to partial shading, there is a very small range of output power maximization.
7. Results and discussions
A matrix size of 9X9 Solar PV modules is linked in a TCT configuration and exposed successively to four shading patterns SW, LW, SN, and LN to assess the effectiveness of the proposed approach. The simulations are carried out for TCT and our proposed MSV using MATLAB/Simulink. The results achieved are compared to TCT for the same shading pattern. Also, P-V curves are used for the analysis of TCT and MSV configurations.
7.1. Long and wide shading pattern
The global maximum power point (GMPP) of TCT and MSV configurations under LW shading pattern is presented in Table 2. Under this pattern, the MSV configuration produces the maximum GMPP at 4146 W. In this shaded condition, it was observed that the MSV configuration increased the GMPP by 33.78% compared to the TCT PV generator configuration by avoiding inadequate power losses.
Table 2 GMPP achieved and percentage of improvement in power with MSV compared to TCT.
| Maximum Power (W) | Power Increase using MSV (%) | ||
|---|---|---|---|
| TCT | MSV | TCT | |
| LW | 3099 | 4146 | 33.78 |
In Figure 9, we plot the calculated P-V characteristics for the TCT and MSV configurations in the case of an LW shading pattern. It can be observed that the electrical P-V features are more linear in MSV, and the global peak is more clearly defined compared with the TCT, which has two local peaks. Also, it is clearly shown in Figure 9 that the output power of the MSV configuration is higher than that of the TCT. Therefore, the PV modules arrangement based on the MSV model will increase the output power produced by the PV array.
7.2. Short and wide shadow
Table 3 presents the global maximum power point (GMPP) of TCT and MSV configurations under a short and wide shading pattern. In this case of partial shading, the MSV configuration reached a maximum power of 4508.08W against 3472.34W for the TCT. So, with the MSV configuration, we obtain an increase in output power of 1036.08 W compared to that of the TCT. This represents a percentage increase of 29.83%, which is rather significant.
Table 3 GMPP achieved and of % increase in output power for MSV compared to TCT.
| GMPP Power (W) | Power increase using MSV (%) | ||
|---|---|---|---|
| TCT | MSV | TCT | |
| SW | 3472.34 | 4508.22 | 29.83 |
In Figure 10, we reported the calculated P-V characteristics for the TCT and MSV configurations in this case of the SW shading pattern. It is clearly shown that the P-V characteristics of the MSV are more linear than the TCT topology, and then the global peak is more clearly defined compared to the TCT, which has multiple local peaks. Therefore, the arrangement of the PV modules according to the MSV configuration improves the power produced by the array. It can, therefore, be concluded that in this case of SW shading, the generated power of the MSV configuration proposed is greater than that of the TCT.
7.3. Long and narrow shadow
Table 4 presents the global maximum power point (GMPP) of TCT and MSV configurations under a LN pattern. In the case of this partial shading, the MSV configuration reached a maximum power of 5152.13 W against 4811.52W for the TCT. So, based on MSV configuration, we can increase the output power by 7.07%, which is rather significant.
Table 4 GMPP achieved and power increase of MSV compared to TCT.
| GMPP Power (W) | Power increase using MSV (%) | ||
|---|---|---|---|
| TCT | MSV | TCT | |
| LN | 4811.52 | 5152.13 | 7.07 |
In Figure 11, we reported the calculated P-V characteristics for the TCT and MSV configurations in the case of a LN shading pattern. It is clearly shown that the P-V characteristics of the MSV are more linear than the remaining topology TCT, and then the Global Peak is more clearly defined compared to the TCT, which has multiple local peaks. Therefore, the arrangement of the PV modules according to the MSV configuration improves the power produced by the array. It can then be concluded that in this case of LN shading, the output power of the MSV configuration is greater than that of the TCT.
7.4. Short and narrow shadow
Table 5 presents the global maximum power point (GMPP) of TCT and MSV configurations under a SN shading pattern. The MSV configuration grasped a maximum power of 5339.00W against 4996.00W for the TCT. So, with the MSV configuration, we obtain an increase in output power of 6.86% compared to that of the TCT. This increase in power is not very large compared to the previous ones.
Table 5 GMPP achieved and percentage of increase in output power for MSV compared to TCT.
| GMPP Power (W) | Power increase using MSV (%) | ||
|---|---|---|---|
| TCT | MSV | TCT | |
| SN | 4996.00 | 5339.00 | 6.86 |
In Figure 12, we reported the calculated P-V characteristics for the TCT and MSV configurations in the SN shading pattern. It is clearly shown that the P-V characteristics of the MSV are more linear than the TCT and then the global peak is more clearly defined compared to the TCT, which has multiple local peaks. Therefore, the arrangement of the PV modules according to the MSV configuration enhances the output power by the array. It can, therefore, be concluded that in this case of SN shading, the generated power of the MSV configuration proposed is also slightly higher than that of the TCT.
8. Comparative analysis
This section will compare our proposed method MSV with some recent literature of PV array reconfiguration under partial shading conditions. We will be particularly interested in comparing the existing magic square method. It is well known that partial shading reduces the output power of the PV array. This power loss due to partial shading is not proportional only to the shaded area but depends on the shading pattern, array configuration, and the location of the shaded modules in the matrix. This is the reason why we will limit the comparison of our MSV method only with the works of the literature, which used the same size of (9x9) PV array, which used the same models of partial shade, and finally used the same irradiance levels. This brings us to the works of Rani et al. (2013) and those of Dhanalakshmi and Rajasekar (2018).
The first author Rani et al. (2013) used SuDoKu (SDK) method to configure the physical placement of the modules in a (9x9) PV array generator connected to the TCT to enhance the PV power generation under partial shading conditions SW, LW, SN, and LN.
The second author Dhanalakshmi and Rajasekar (2018), used the same four partial shadow conditions in a (9x9) photovoltaic generator reconfigured according to the competence square (CS) method. The results obtained by these authors compared them with TCT and dominance square (DS) techniques.
Our MSV arrangement outperformed other CS, DS, and SuDoKu approaches in terms of total performance, and all of them are compared to TCT in terms of the percentage power enhancement, which is the power difference between the conventional and proposed value at global power peak is termed as PE (%) power enhancement. The PV system's power enhancement, PE (%) is given in Equation (9).
Our results and those of the literature are grouped in Table 6. On Table 6 are reported the global maximum power point GMPP in Watt for all these configurations and for all the partial shading patterns studied. It is also reproduced in Table 6, the power enhancement percentages of the SuDoKu, MSV, DS, and CS configurations compared to the TCT technique calculated for all the partial shading patterns studied.
Table 6 Comparison of our results and those of the literature.
| Rani et al. (2013) | Our Results | Dhanalakshmi and Rajasekar (2018) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Maximum Power (W) | %PE | Maximum Power (W) | %PE | Maximum Power (W) | %PE | %PE | |||||
| Case | TCT | SDK | TCT | MSV | TCT | DS | CS | ||||
| SW | 3348 | 4532 | 26.1 | 3472 | 4508 | 22.97 | 3422 | 4372 | 21.72 | 4532 | 24.49 |
| LW | 3244 | 4083 | 20.5 | 3099 | 4146 | 25.15 | 3203 | 3916 | 18.2 | 4096 | 21.6 |
| SN | 4711 | 5045 | 6.6 | 4996 | 5339 | 6.42 | 5258 | 5502 | 4.43 | 5630 | 6.6 |
| LN | 4703 | 4879 | 3.6 | 4811 | 5152 | 6.61 | 4341 | 4647 | 6.58 | 5094 | 14.7 |
We note that our results are in good agreement with those of the literature. We also note that for all the shading patterns, the results show that the SuDoKu, MSV, DS, and CS configurations give good performance compared to the conventional TCT arrangement. This improvement in performance exceeds 20% for the shade case of SW and LW and is less important in the cases of SN and LN shading patterns.
Finally, we can clearly see that our MSV method gives the best performance compared to all other configurations for the LW type shading case. Indeed, with the MSV configuration, we obtain a power enhancement of 25.15% for the partial shading type LW against 20.5%, 18.2%, and 21.6% obtained with the SuDoKu, DS, and CS methods, respectively. We can, therefore, conclude that our MSV method is more efficient in the case of partial LW type shading. This would certainly be due to the vital capacity of the MSV technique to disperse the shadow of a large pattern on many photovoltaic modules.
We would like to point out that there are other techniques for spreading partial shadows in the literature that we did not study in this comparative analysis, although they have also proven to be efficient. This is justified by the fact that these techniques use PV arrays of different sizes and different shading patterns compared to those we used. Among the most recent of these techniques, there is the magic square puzzle (MSP) proposed.
By Yadav et al. (2017) its analysis has been carried out on a (4x4) PV array configuration for three different shading patterns (vertical, horizontal, and diagonal shading). From its results, it is found that the MSP configuration achieves a maximum power increase of 13.3% compared to the TCT method.
John Bosco and Carolin Mabel (2017) proposed a Cross Diagonal View (CVD) configuration used in a (9×9) PV array system for the dispersion of three shading patterns whose location is different from the conventional shading patterns we used in our calculation. The proposed CDV configuration has shown an average increase in power enhancement of 21.67%, compared to TCT for the three shadings considered.
Finally, Vijayalekshmy et al. (2016a) proposed a Novel Total Cross Tied configuration (Zig-Zag scheme) for performance improvement under partial shading conditions of a (4x3) PV array. In this work, five easy to forecast short-term sources of partial shading are analyzed. Since the GMPP under all cases of partial shading is equal, the power enhancement is the same for the studied configurations.
9. Conclusion
We can distribute the partial shade models throughout the full solar generator through the magic square view arrangement. A further advantage of the MSV configuration is that it may be used to enormous matrixes since it uses a reconnection mechanism. For large-scale solar plants, the MSV configuration technique may be used to build efficient systems. The complexity of MPPT (maximum power point tracker) may be simplified using the MSV, enabling us to have more uniform electrical characteristics (P-V) and a few local maximum values.
In this work, the performance of (9×9) PV array configurations MSV compared to TCT are studied and carried out with MATLAB/Simulink systems. Four different shading patterns such as SW, LW, SN, and LN are investigated, and the obtained results are compared with existing TCT and with some recent techniques from the literature.
From our results, it is observed that the PV array can reach a power increase of 33.78% under shading pattern LW, and 29.83% under pattern SW compared to TCT configuration if their interconnects are well connected according to the magic square view configuration. Further, we can achieve an increase in power of 7.07% and 6.86% under the shading patterns LN and SN, respectively.
The extensive analysis and the whole statistical results prove the proposed methods' efficiency compared to TCT to enhance the output power of large photovoltaic arrays for all the partial shading patterns studied.
According to the results of the comparative analysis, it is found that the SuDoKu, MSV, DS, and CS methods have shown their high efficiency for LW and SW shading patterns compared to LN and SN.
Also, from the comparative analysis results, we can see that the MSV technique gives better performances compared to the other techniques, particularly for LW partial shading pattern.
Indeed, the MSV technique achieves a maximum power enhancement of up to 25.15% for the shadow case of LW compared to the TCT against 20.5%, 18.2%, and 21.6% obtained for SuDoKu, DS, and CS methods, respectively. Thus, our proposed MSV technique proves its effectiveness compared to SuDoku, DS, and CS, especially in strong shading patterns. The MSV acts as a radiance balancing method of keeping as many shaded or unshaded modules on the same string as possible.
An excellent set of tools for distributing partial shade is supplied by the view magic square approach, and the goal is to increase PV system performance.











 nueva página del texto (beta)
nueva página del texto (beta)












