1. Introduction

Dopamine (DA) is a neurotransmitter produced in the human body in a natural way. This compound plays an important role in the regulation of hormonal secretion in the central nervous system and organs involved in the control of motor, cognition and neuroendocrine functions. Furthermore, this is present in regions of the brain that regulate movement and emotion. ^[1] An improper regulation of this neurotransmitter is associated with neurological diseases such as Parkinsonism, where dopamine levels are reduced, or schizophrenia, where a high activity of dopamine has been registered. ^[2-4] By its structure, DA can be a precursor in the synthesis of other catecholamines in the human body, like epinephrine and norepinephrine. ^[5] There is evidence that catecholamines neurotransmitters, like dopamine, show antioxidant activity and consequently reactive oxygen species (ROS) react with these compounds under oxidative stress conditions, ^[6-14] inducing neuroprotective effects. Structurally, DA is formed by a catechol fraction and one aliphatic chain with a terminal amino group (Fig. 1). The catechol moiety in this compound is considered as a powerful antioxidant. ^[15-16]

Fig. 1 Dopamine. 

By the side of theoretical studies, there is one report where a computational kinetic study is carried out on the reactivity of dopamine toward hydroxyl (•OH) and hydroperoxyl (•OOH) free radicals, in aqueous and lipidic simulated biological environments. The main interest of this study is the evaluation of its free radical scavenging capacity. In such a work, the authors propose a mechanism of the reaction as a sequential electron proton transfer and hydrogen atom transfer. For the first step, the electron detachment is carried out in the catechol moiety, hence the importance of this group in the properties of dopamine. Finally, they conclude that DA is a very good •OOH, and presumably •OOR, radical scavenger. ^[17] In addition of this work, Lu and Yu estimated theoretically the ionization potential, on different conformations, of the dopamine. The study deals with two molecular geometries. One, where an intramolecular hydrogen bond (IHB) is present on the -OH in catechol moiety, and the another one, where the -OH groups are in one opposite direction, and consequently the contact O-H···O is not present. Thus, the involved IHB lies in the definition by the IUPAC about a hydrogen bond, where donor and acceptor are two atoms with high electronegativity.^[18]

They conclude that the conformers with the IHB are more stable, nevertheless, the ionization potential of both conformers does not differ appreciably. ^[19] On this direction, several theoretical investigations have been reported about the formation of the IHB, and its role, on systems with catecholic rings. In particular, Ortega-Moo et al., have characterized this contact over some substituted catechols, by using three scalar fields, the non-covalent interaction index, the electron density through the atoms in molecules theory and the electron localization function. From their results, none of the scalar fields used ensures that an IHB is present in these kind of compounds, ^[20] giving important information about this possible contact. In addition, Ortega-Moo et al. show that this contact is totally irrelevant to describe several chemical reactivity indicators.

In our knowledge, one study related to chemical reactivity indicators for dopamine is still missing. It is well known that within the density functional theory (DFT) framework, there are several indicators that are useful to predict the most reactive sites in a molecule. ^[21,22] For this reason, in this short report, several chemical reactivity indicators defined within the DFT framework are used to study the dopamine. The aim of this study is to predict the sites where the dopamine donates electrons and how these sites are modified if an intramolecular hydrogen bond is present or not.

2. Theory

In DFT, two groups of reactivity indices allow the study of any chemical system; global and local. ^[21,22] On the side of global predictors, the chemical potential (μ) ^[23] and the hardness (η) ^[24] are defined as

, (1)

, (2)

where E and N represent the total energy and the number of electrons of the system, respectively. From these definitions, clearly the external potential, v(r), is fixed. For molecular systems, this restriction means that all nuclei keep their positions when the system accepts or gives electrons. By using a finite difference approximation, μ and η can be evaluated as

, (3)

, (4)

where I is the ionization potential and A the electronic affinity. Another global reactivity index, defined by Parr et. al. is the electrophilicity written as ^[25]

. (5)

This quantity determines the susceptibility in one molecule to accept electrons. For the evaluation of these quantities, the discontinuity in the derivatives has been recognized from initial stages of the DFT. For that reason, Gázquez, Cedillo and Vela, proposed the electroaccepting (ω⁺) and electrodonating (ω⁻) powers, ^[26,27] associated with the acceptance and donation of charge in a molecular system. These quantities are defined as

, (6)

, (7)

where μ⁺ and μ^- are defined by

, (8)

. (9)

Within the finite difference approximation, these quantities are obtained from

, (10)

. (11)

On the side of local reactivity, Parr and Yang proposed the Fukui function ^[28]

, (12)

as one quantity to identify regions of the system where the density responses when the number of electrons is modified. Thus, f ⁻ predicts sites where the system is susceptible of one electrophilic attack,

, (13)

while f ⁺ predicts sites where nucleophilic attacks are expected, through the expression

. (14)

In addition, it is quite useful the definition of regional values for these local quantities. Sometimes, regional or condensed Fukui functions are obtained from

, (15)

. (16)

In these equations, q_i represents an atomic charge, defined by qi ≡ Zi - Qi, where Zi is the atomic number and Qi the electronic charge on ith atom, which is estimated by using a population analysis like those obtained from Mulliken, ^[29] Merz-Singh-Kollman ^[30,31] or Hirshfeld, ^[32] at the ith atomic site. Connecting Fukui functions and electro-donor or -acceptor powers, the local electroaccepting [ω⁺(r)] and electrodonating [ω⁻(r)] powers are defined as

, (17)

. (18)

Naturally, their corresponding condensed quantities are obtained from eqs. 15 and 16.

3. Computational details

All calculations were done with the NWChem v6.3 suite code.^[33] For this study, three conformations of the dopamine were considered, two of them forming an intramolecular hydrogen bond (IHB) between OH groups in catechol moiety. Thus, from Fig. 1, one IHB (DA₁) is formed between O1 and H5 and a second IHB (DA₂) is formed between O2 and H4. An additional confomer (DA_wo) was considered, where no IHB is present. Geometry optimizations and frequency analysis were carried out by using the PBE0 exchange-correlation functional.^[34] In addition, the second-order many-body perturbation theory, MP2, ^[35] was considered just for the geometrical analysis. For all methods, 6-31+G(d), 6-311+G(d) and 6-311+ +G(d,p) basis sets were used to see basis set effects on geometrical parameters. ^[36] In order to test one hypothesis proposed in this work, eight additional compounds were considered, with and without IHB. These compounds are based on the catechol moiety, which correspond to those studied by Ortega et al.^[20], these structures are represented in Fig. 2. By the side of reactivity descriptors, the systems were analyzed by using the PBE0/6-311 ++G(d,p) method.

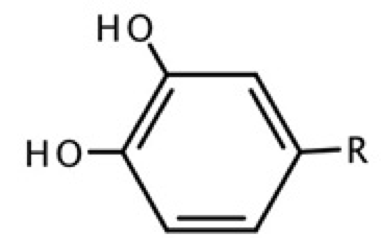
Fig. 2 Structures obtained from Ortega et al. ^[20] with R=H, CH₃, CH₂CH₃, (CH₂)₂CH₃, CH=CH₂, CH=CHCOOH, CO(CH₂)₄CH₃, COOH. 

The electron affinity was estimated from

, (19)

and the ionization potential from

. (20)

Global predictors as hardness (η), ^[24] chemical potential (μ), ^[23] electrodonating (ω⁻) and electroaccepting (ω⁺) powers ^[26,27] were evaluated by using I and A estimated from eqs. 19 and 20. In order to obtain information about the reactivity sites in dopamine, the Fukui functions and condensed values of local predictors were necessary. In this work, the partial atomic charges that fit the molecular electrostatic potential were used to calculate the condensed Fukui functions and from here local electrodonating and electroaccepting powers. ^[26,27]

4. Results and discussion

4.1 Geometry analysis

The dopamine conformers considered in this work are presented in Fig. 3. For this compound, the MP2/6-311++G(d,p) method predicts DA₁ and DA₂ more stable than DA_wo by 4.6 kcal/mol respect to DA₁ and 4.1 kcal/mol respect to DA₂, while the PBE0/6-311++G(d,p) shows a difference of 4.2 kcal/mol and 4.4 kcal/mol, respectively. For the catechol, this energy difference is of 4.1 kcal/mol ^[37] and for systems related with catechol also exhibit an energy difference of 4.1 kcal/mol. ^[20] Thus, estimations given in this work, deliver similar information to results reported in other studies. Some geometrical parameters obtained for DA₁, DA₂ and DA_wo are reported in Table 1.

Fig. 3 Conformers of dopamine optimized with MP2/6-311++G(d,p) method. 

Table 1 Some structural parameters for three conformers of dopamine, DA₁/DA₂/DA_wo 

By using the MP2/6-311++G(d,p) method as reference, it is clear that one additional diffuse function and one additional polarization function have important impact on MP2 calculations but not for PBE0, since for PBE0 the differences are almost zero between 6-311+G(d) and 6-311++G(d,p) basis sets. In fact, we can say that even the small basis set 6-31+G(d) gives similar results than those obtained by the biggest one. We must recognize that the difference found between PBE0 and MP2 with the largest basis set are rather small. Thus, we can conclude that for dopamine the PBE0 exchange-correlation functional works well to predict its geometrical structure. The same conclusion is reached when the D3 Grimme dispersion approximation ^[38] is applied over the same systems. For that reason, we use only the PBE0 exchange-correlation functional.

4.3 Local reactivity descriptors

In last section, it was shown that global chemical predictors for processes where dopamine gives charge, do not change appreciably when the IHB is considered or not. In this section, some local reactivity predictors are explored to see if the same conclusion is valid locally. For this goal, Fukui functions are the quantities to be explored. In this work, f ⁻ (r) and f ⁺(r) have been evaluated as a difference between electron densities, according to eqs. 13 and 14. For a process where the dopamine donates charge, the corresponding f ⁻ (r) is presented in Fig. 4 for DA₁, DA₂ and DA_wo. From a visual analysis, it is not possible distinguish differences among the conformers, since for all cases the biggest response of this quantity is found over the atoms O1, O2, C1, C3, C4, C6 and N1. Also for the three conformers, the f ⁻ has important contributions over the bonds defined by the atoms C4-C6 and C1-C3. This is an interesting result since OH groups have an important impact on the atoms where they are binded, however, the delocalization involved within the ring induces important changes on C1 and C3 atoms and over the C1-C3 bond.

Fig. 4 Fukui function (f ⁻) for (a) DA₁, (b) DA₂ and (c) DA_wo 

At this point, a visual analysis has been discussed around DA₁, DA₂ and DA_wo conformers, although a quantitative analysis is necessary to give conclusions. For this reason, a population analysis is needed, which is presented in Table 3, where the condensed local electro-donating and - accepting powers are reported for atoms that exhibit ω_c > 0.1. In principle, large values of this quantity indicate sites where the system prefers to donate or accept electrons, in our case we will focus the discussion on ω^- _c. For DA₁, it is evident that C1, N1, O2 and C3 are the four atoms with the biggest value of ω^- _c and for DA₂, the atoms with the biggest response are C₁, N_1, O₁ and C₃. This observation gives one important conclusion, oxygen atoms acting as acceptors (O_A) to form a hydrogen bond reduce their response to give electrons. This result has sense since these atoms provide electrons to form a hydrogen bond. In addition, we found that ω^- _OD ≈ 2ω^- _OA, where O_D represents an oxygen atom acting as donor in a hydrogen bond.

Table 3 Electrodonating and electroaccepting powers for DA₁, DA₂ and DA_wo by using PBE0/6-311++G(d,p). All values are in a.u. 

From Table 3 and Fig. 4, there is an interesting result. We mentioned above, from Fig. 4, that ω⁻(r) is localized between C1 and C3 (including both atoms). We will assume that the information of ω⁻(r) along the C1-C3 bond is contained in the condensed information of C1 and C3. Therefore, we propose that for bound regions where the ω⁻(r) is delocalized, the corresponding condensed information is obtained from the sum of the sites that bound such a region. Thus, ω^- _C1 + ω^- _C3 = 1.1 for DA₁ and 1.2 for DA₂, represent the biggest value of the condensed local electroaccepting power. We conclude that the detachment of one electron from the DA will be trough the region defined by the C1-C3 bond. By doing the same analysis on the DA_wo structure, it is impressive the response obtained for the oxygen atoms. Both atoms acquire almost same values for the condensed ω⁻, and the region defined by C1 and C3 keeps almost the same value (1.2 a.u.). These results are quite important since the IHB observed in the dopamine is not relevant for global quantities, like total energy, ionization potential or η. However, we are showing that this contact has an important impact on the local electrodonating power. To corroborate this conclusion, eight additional catechol derivatives were tested, such compounds correspond to those reported in Fig. 3 of reference ^[20] and Fig. 2 of this report, where the substituent is changed on the para position. For this case, the evaluation of f ^-C is enough to validate our conclusions, which is reported in Table 4. From here, there is no a doubt that the reactivity of the oxygen atoms in the catechol moiety is the same when the IHB is not present. Contrary to this behavior, if the IHB is present then these atoms respond in a different way. Additionally, C1 and C3 atoms show the biggest values for f ^{- C} among all atoms in the nine tested systems, and f ^{- C} ₁ + f ^- _{C 3} present the biggest value.

Table 4 Condensed f ⁻ for dopamine and eight derivatives of the catechol. For this case the substituents are: 1) H, 2) CH₃, 3) CH₂CH₃, 4) (CH₂)₂CH₃, 5) CH=CH₂, 6) CH=CHCOOH, 7) COOH, 8) CO(CH₂)₄COOH. All quantities are in a.u. 

5. Conclusions

In this work, three conformations of the dopamine were analyzed by using DFT descriptors, ω⁺(r) and ω⁻(r). The results suggest that dopamine is not good acceptor of charge. It was possible to observe that when an electrophilic attack occurs, the catechol moiety is the preferred site, especially the region defined by the atoms C1 and C3. The most important result found in this short report, is the influence of the intramolecular hydrogen bond over local reactivity descriptors and not over the global counterpart. Such a conclusion was obtained with nine analyzed system, all related with catechol derivatives.