1. Introduction

In the study of physical phenomena of a real system, models are commonly used. A model is a well-defined mathematical process associated with the real system which is the subject matter of study. These models represent a simplified version of the physical phenomenon. The selected model includes a set of variables that completely characterize the system, in which a small number of interactions are omitted or taken into account. An example of the above is the interaction between particles forming a physical system in the presence of a conservative force field; in this case the total work exerted over the system on a closed path vanishes and at any point of the path its mechanical energy is constant, that is, the system is conservative.

Every physical system is not isolated, it is found inmersed in a larger system called environment. The environment is not manipulable due to the great number of degrees of freedom. Information on the evolution of the system can only be obtained from the phenomenological equations of motion. The latter is established from experimental information even when the explicit interaction is not known ¹. The majority of physical phenomena are irreversible: diffusion and dissipation are examples, whereby the mechanical energy is transformed into heat. This dissipation can be observed through the interaction between the system of interest and its environment ². Accordingly, and due to its complexity, an important issue of scientific interest is to study more real physical systems where irreversible and dissipative properties are present, whether or not its environment is known.

Dissipative systems are non-Hamiltonian. Among these systems we can mention: Systems with macroscopic friction that can be well described by Newtonian mechanics, the damped harmonic oscillator (probably the standard example of a dissipative system) which can be described through an explicitly time-dependent Hamiltonian, and the loaded oscillator in an RLC linear circuit. The starting point for the understanding of dissipative systems can be established in 1931. Historically, Bateman was the first to propose the time dependent Hamiltonian in the classic context which describes the damped oscillations ³. Later on, P. Cardilora and E. Kanai, independently constructed from Bateman’s Hamiltonian, the Hamilton function of Caldirola-Kanai (H _CK ) using a time dependent canonical transformation ^4,5; with H _CK the equation of motion is provided. This equation describes the behavior of a constant frequency and time-varying mass oscillator. A comparative study of this model with the Lane-Emden damped harmonic oscillator model is carried out by Ozeren F. and Aguiar V. Works in the opposite direction have been proposed using purely geometric considerations, to find Bateman’s Hamiltonian from that of Caldirola-Kanai ^6,7,8.

Along with the birth of quantum mechanics birth, there has been a constant interest in the dissipative systems with the inherent difficulties to describe damping in the harmonic oscillator. In Schrödinger’s representation the H _CK Hamiltonian is used with the problem that quantization does not comply with the uncertainty relations. Brittin carried out an extensive study when addressing this type of quantum mechanical solutions that violate the uncertainty principle ⁹. A attempt to overcome this difficulty is shown in Dedene’s work ¹⁰, who within the geometric field quantization develops a sympletic formulation for the damped harmonic oscillator based on Dekker’s dynamic variables ¹¹. L. Pedrosa, solved the Schrödinger’s equation using an auxiliary function of Milney-Pinney’s equation, obtaining the wave function for H _CK with and without the presence of a singular potential ¹². A detailed research of two kinds of time dependent damped harmonic oscillators including oscillators with H _CK is presented by Bessa V. As a result quantum solutions through unitary transformations with Lewis-Reisenfeld invariant method are obtained ¹³.

In addition to the methods described in the preceding paragraph for studying dissipative systems in a quantum mechanical context, there is also the propagator evaluation. Cheng evaluates the propagator for H _CK , and obtains the time dependent wave function corresponding to the propagator; nevertheless, the exact wave function is not obtained ¹⁴. O. Roldan, presents the H _CK model for the damped harmonic oscillator using path integrals to calculate the propagator with which the evolution of a squeezed state is obtained, and variances of the position and momentum are calculated ¹⁵. Currently, there are formally established descriptions for studying dissipative systems such as Schrödinger-Langevin equation (derived from Heisenberg equations of motion) ¹⁶, Weyl’s generalized quantization ¹⁷, unitary transformations for damped and forced harmonic oscillator ¹⁸, Schrödinger variational principle by Razavy ¹⁹, and the stochastic method by Nelson ²⁰.

As described throughout this work, the study of dissipative systems and in particular that of Caldirola-Kanai oscillator, is a field under continuous research from classical as well as from the quantum point of view. In this present work we are interested in presenting the method for solving Hamilton-Jacobi equation for the oscillator damped with Caldirola-Kanai Hamiltonian. The work has been organized in the following manner: in Sec. 2 we present the fundamental concepts of Lagrange and Hamilton-Jacobi equations, in Sec. 3 we present the Caldirola-Kanai Hamiltonian, in Sec. 4 the solution of Hamilton-Jacobi equation and in Sec. 5 the obtained results and discussion. Finally, the conclusions and bibliography are given.

2. Lagrange and Hamilton-Jacobi equations

Historically, the main statements of Newtonian mechanics are the three axioms, with which the solution to the motion problem was proposed. Nevertheless, it is not the only conceptual scheme that allows to address that problem. The development of classical mechanics was marked by two paths: vector mechanics and analytic mechanics ²¹. Vector mechanics directly starts from the laws of motion. It is based on linear momentum and force vectors. Knowing the forces acting on a particle along with the initial conditions (position and velocity) allows to describe its time evolution.

The path followed by analytic mechanics traces back to the XVIII century. In 1774, the French mathematician Pierre Louis Moureau de Maupertuis, enunciated his famous principle of minimum action. Starting from Fermat’s principle, Moureau de Maupertuis used another quantity called action which is defined as the product of mass m, times the velocity v and times the distance s travelled by the particle ²². In that same year, Euler wrote the Maupertuis principle of minimum action as follows:

Despite the fact that Euler sketched this first dynamic interpretation of Maupertuis principle, the credit for the use of the principle of minimum action is attributed to Lagrange, who with the purpose of defining the configuration of a system of particles, introduced the concept of generalized coordinates (q _i , p _i ) and using variational calculus obtained the Euler Lagrange-Poisson Equation ²³

Where L = T - V is the so-called Lagrange function. At this point, we can establish that analytic mechanics is grounded on scalar magnitudes, kinetics energy and potential energy. Magnitudes associated with the body and its motion, in this formulation force has not been considered as a fundamental concept.

In 1835, William Hamilton observed that equation (2) referred to only conservative systems, wherein potential V is only a function of the coordinates q _i . Hamilton generalized the results by including non-conservative systems for which V=V(qi̇,qi,t) enunciating his principle known since then as Hamilton’s Principle ²⁴,

In addition, to a mechanical system whose dynamics is described by (2) in phase space it is associated with an H(q, p, t) function, named Hamiltonian function (Hamiltonian). In general, this function depends on the state variables (q _i , p _i ) and on time t. The Hamiltonian of the mechanical system is given by:

The above relation is a Legendre transformation which allows to turn the set of Lagrangian’s variables into the set of Hamiltonian variables, the generalized Hamilton equations are

Let us go on now with Hamilton-Jacobi theory, widely detailed in the classical mechanics texts, such as that of Goldstein ²⁵. The Hamilton-Jacobi formalism central idea is to search for a canonical transformation of coordinates and momentum (q, p) for a time t, into a new set of constant quantities, which can be the initial values of (Q, P) for t ₀; the points (q, p) and (Q, P) represent the state of the system at instants t and t ₀. By definition, the transformation is canonical if Hamilton equation (5) are satisfied. As variables (Q, P) represent the initial state of the system, these quantities do not change with time. For this to happen, the transformed Hamiltonian H´(Q, P, t), cannot depend on either Q or P, that is, H´ must be identically zero.

Then, every cyclic coordinate is related to a first integral (its conjugated momentum), so that a canonical transformation turning into a set of cyclic coordinates, would ensure the resolution of a mechanical problem. The generating function verifying the purpose that the new Hamiltonian was zero, is called the Hamilton main function and is a second class generating function S(q, P, t) such that ²⁶:

with,

Given that H´ = 0, all Q´s are cyclic and their conjugated momentum are constant. The equation

is called Hamilton-Jacobi Equation and can be interpreted as a partial differential equation for S. In this equation there are n + 1 variables, the nq´s and time. The general solution for S depends on n + 1 constants, one of them being additive. As (8) depends on the S derivatives, then S + constant is also a solution, since the additive constant is irrelevant in the canonical transformation.

3. Caldirola-Kanai Hamiltonian

Euler-Lagrange-Poisson equations (2) correspond to the equations of motion of a system characterized by a Lagrangean function. Unlike the simple harmonic oscillator where one can easily obtain the equation of motion ²⁷, in the case of the damped harmonic oscillator, obtaining the equation of motion is not direct. A first attempt was presented by Rayleigh, by introducing a dissipative function F in (2),

of the form of F=λq̇2/2 ²⁴. The well-known equation of motion for a damped harmonic oscillator is obtained

Although Eq. (10) represents the movement equation for dissipative systems, it is a phenomenological description of these systems as there is not any Lagrangean, nor any variational principle that has been involved. The first attempts to understand this difficulty were presented by Bateman, Caldirola and Kanai by presenting a Lagrangian which in the case of a one-dimension is given by:

with damping coefficient γ=λ/m and the oscillation frequency w. The corresponding Caldirola-Kanai Hamiltonian is obtained from (4),

apparently depending on t; however, it does not generally represent dissipative systems but it does represent physical systems with an exponentially increasing mass with time m(t)=meγt.

4. Solution of Hamilton-Jacobi equation for the oscillator with Caldirola-Kanai Hamiltonian

Replacing in the Euler-Lagrange-Poisson equations (2) with (11), the equation of a damped harmonic motion (10) is obtained. In the Herrera L.’s paper, it is proposed that in the motion of a damped system from a time t ₁ to t ₂, the action ²⁸

has a stationary value for the correct movement path, where L ₀ is the Lagrangean of a conservative system, T - V. When defining a canonical transformation

the new canonical variables Q and P satisfy the variational principle,

H´ is the new Hamiltonian. When considering the following canonical transformations,

the generating function is given by:

with,

The new Hamiltonian is

Which does not explicitly depend on time, the Hamilton-Jacobi equation for H´ is

In addition, we can separate the time variable with the ansatz S(Q,α,t)=W(Q,α)-αt, with W the Hamilton characteristic function, (20) is expressed in the form

Thus we obtain a quadratic equation in ∂W∂Q, its solution is

After integrating (22) we found the characteristic function, the result obtained was derived with respect to α.

From the above expression we solve for Q taking into account that ∂W/∂α=t+β, ²⁴

with Ω=w2-(γ2/4), the constants α and β are determined through the initial conditions. Finally the solution in terms of the original variable (16) is:

The above result represents the time variation of q with decreasing amplitude: a similar behavior for the case of a damped harmonic oscillator (sub-critically). Now we present the results obtained in Sec. 3 making use of the mathematical package Wolfram Mathematica 10.0.

5. Results and discussion

For the Caldirola-Kanai oscillator, the equation of motion is identical to Eq. (10). The variation of the position q(t) given by solution (25), is shown in Fig. 1 for the different values of the damping constant. It has been observed that q(t) oscillates with a decreasing amplitude as γ increases and reaches zero for asymptotic times. The behavior shown is similar to that of a harmonic oscillator with subcritical damping (γ<2w). Furthermore, in the limit γ≈0, the resulting motion is equal to that of a simple harmonic oscillator. The results obtained coincide with those reported in Ref. ⁷.

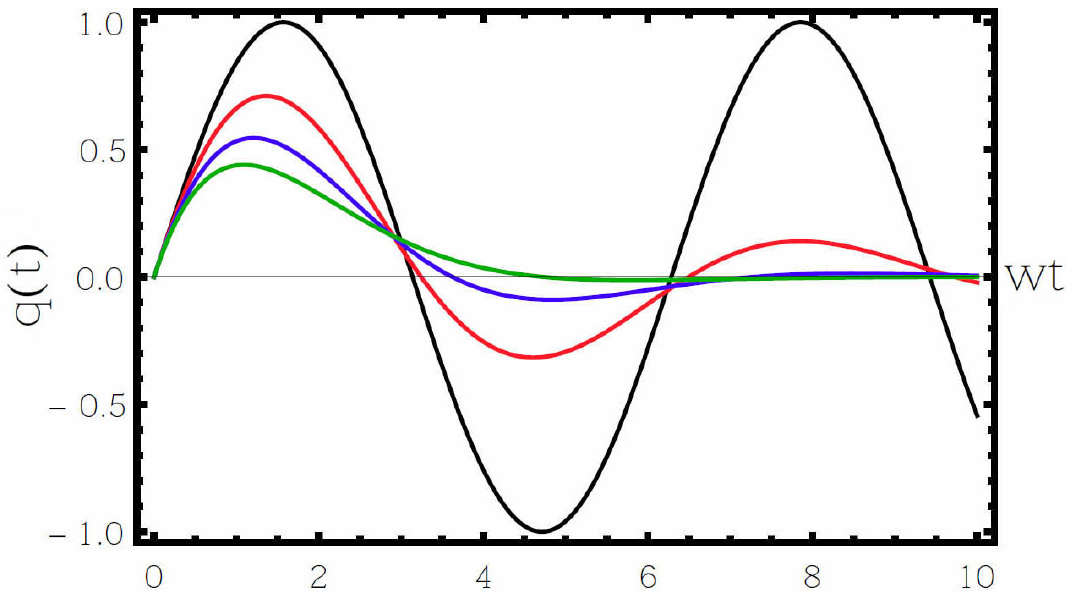
Figure 1. Variation of position q(t) for different values of γ. Color curves: black γ≈0.0, red γ<w/2, blue γ<w and green γ<2w. 

Figure 2 represents the canonical momentum p(t) for a value of the constant γ<0.4w. It is observed that the behavior is different from that expected one in a damped harmonic oscillator, where p(t) increases as time increases. This is due to the exponential increase of the Caldirola-Kanai oscillator mass. Only when damping is null, the behavior is identical to that of an oscillator with simple harmonic motion ²³, see Fig. 3.

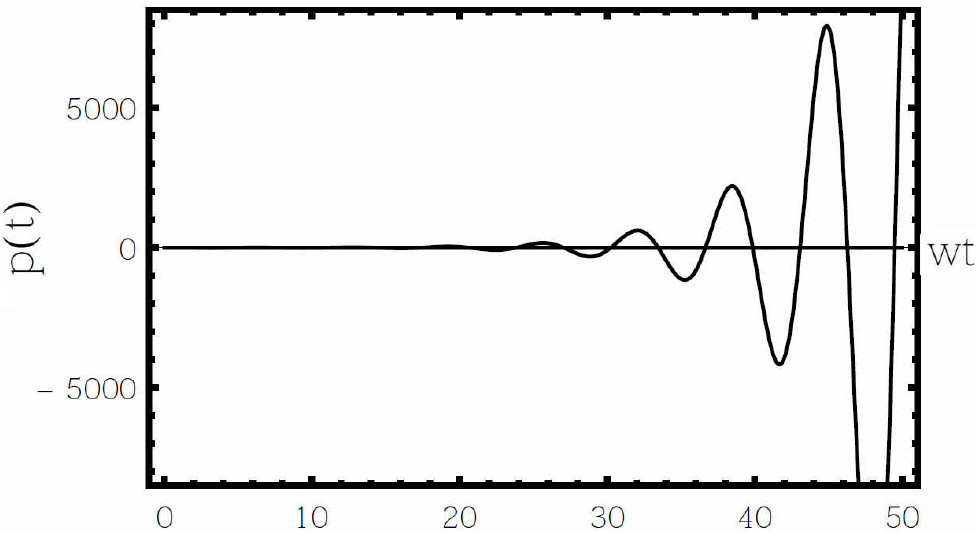
Figure 2. Variation of momentum p(t) for the oscillator with Caldirola-Kanai Hamiltonian with γ<0.4w. 

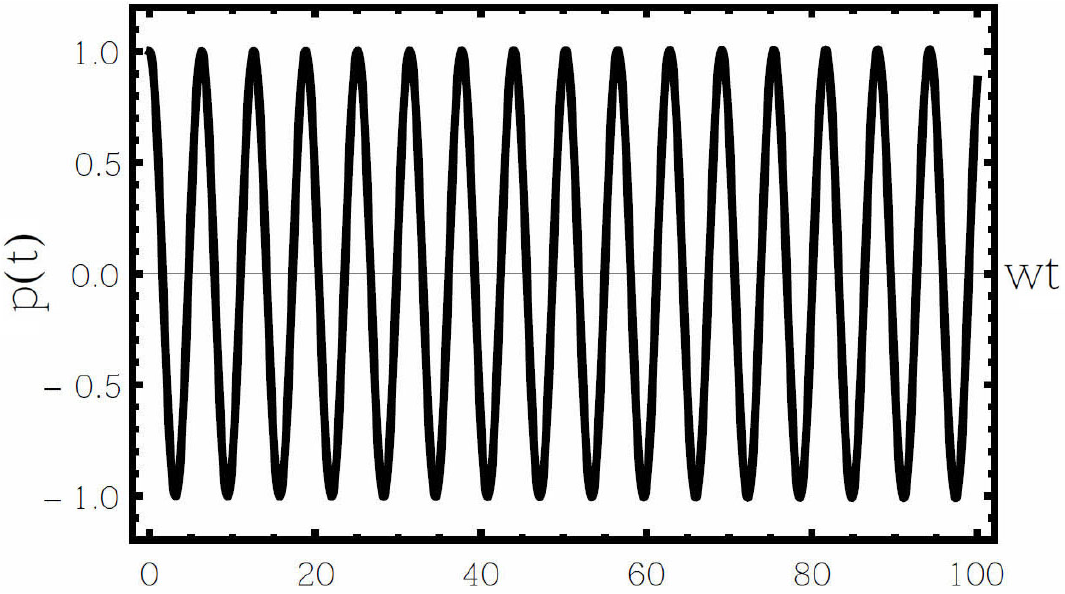
Figure 3. Variation of momentum p(t) for the oscillator with Caldirola-Kanai Hamiltonian with γ=0.0. 

Despite that from the Caldirola-Kanai Hamiltonian (12), the equation of motion of a damped harmonic oscillator is obtained, it could be inferred that the mechanical energy must exponentially decrease with t as it occurs with dissipative systems. However, this Hamiltonian does not represent dissipative systems since when replacing (25) in (12) it is demonstrated that

with t'=t+β. The time average value of (26) is

Thus, it is proven that H is a constant as it was demonstrated by J. Ray, ²⁹ in 1979. The Lagrangean (11) and therefore Hamiltonian (12) do not represent dissipative systems, but they do represent variable mass physical systems in the time.

6. Conclusions

Within the Hamilton-Jacobi theoretical framework through the separation method of variables S(Q,α,t)=W(Q,α)-αt, we solved the equation of motion for the oscillator with Caldirola-Kanai Hamiltonian. We found out that the exponential decrease with time of the position of the oscillator increases as the damping parameter increases; this behavior is identical to that of a sub-damped harmonic oscillator. The results coincide with those reported in V. Aguiar, and I. Guides, ⁷. However, this system does not represent a dissipative system as the momentum p(t) increases with time and it has been demonstrated that the time average value of the Hamiltonian is constant.