PACS: 24.10.Ht; 25.70.-z
1. Introduction
The choice of the nuclear potential is an important parameter to explain the nuclear interactions such as elastic, inelastic and fusion. To produce nuclear potential of any nuclear reaction, different potential forms can be used. With this goal, the phenomenological and double folding potentials 1,2,3,4 have been widely applied in theoretical analysis of nuclear interactions. However, investigation of different nuclear potentials is still a hot topic in the field of the nuclear physics. The nucleus-nucleus potential has not yet been unequivocally described 5, although the Coulomb potential due to the charge of the nuclei is well described at the present time. Therefore, the introduction of alternative potentials will be important in explaining different nuclear interactions such as elastic scattering, inelastic scattering, and coupled channels.
In the present study, we are trying to discover alternative potentials to explain scattering cross sections. With this goal, we explore behaviors of proximity potentials in defining the nuclear interaction of two colliding nuclei. These potentials are widely used in fusion calculations 6,7. However, as we know from the literature, there is not a comprehensive study about applicability of proximity potentials in determining scattering observables of nuclear reactions. In this context, for the first-time, we employ six different proximity potentials to define the elastic scattering angular distributions of 13C on 12C, 16O, 28Si and 208Pb target nuclei at various incident energies. Then, we compare theoretical results with each other as well as the experimental data.
In next section, a short presentation of nuclear potentials and theoretical calculation is provided. The results and discussion are given in Sec. 3. Section 4 is attributed to the summary and conclusions.
2. Theoretical Formalism
In this section, we give a brief description of optical model (OM) and proximity potentials used in fitting the elastic scattering data of 13C projectile by 12C, 16O, 28Si and 208Pb. We use the OM as the theoretical model. For proximity potentials, we examine six different potentials consisting of Broglia and Winther 1991 (BW 91) 8, Aage Winther (AW 91) 9, Christensen and Winther 1976 (CW 76) 10, Bass 1973 (Bass 73) 11,12, Bass 1977 (Bass 77) 13 and Bass 1980 (Bass 80) 8.
2.1. Proximity Potentials
2.1.1. Broglia and Winther 1991 (BW 91) potential
In this approach, the real part of the optical potential is assumed as 14
where
and
with surface energy constant
where
2.1.2. Aage Winther (AW 95) Potential
The second kind potential employed for the real part is the same as the BW 91 potential except for 14
and
2.1.3. Christensen and Winther 1976 (CW 76) Potential
Another form of the real potential analyzed with this work is written as 15
where
The universal function
2.1.4. Bass 1973 (Bass 73) Potential
The fourth potential for the real part is parameterized as 15
where
2.1.5. Bass 1977 (Bass 77) Potential
Another real potential is in the following form 14
where
The function
where A = 0.030 MeV-1 fm, B = 0.0061 MeV-1 fm, d1 = 3.30 fm and d2 = 0.65 fm.
2.1.6. Bass 1980 (Bass 80) Potential
This potential is the same as the Bass 77 potential form. Only the function
and
where i =1, 2 are mass numbers of projectile and target nuclei, respectively.
2.2. Optical Model
The OM which has two potentials as the real and imaginary is an efficient model for calculating the elastic scattering cross section. To obtain the real part of the optical potential in our study, proximity potentials have been evaluated. Each of these potentials has been described in the previous section. The imaginary part has been taken as the Woods-Saxon (WS) potential for all the theoretical calculations, which is given by
Thus, the total interaction potential between projectile and target nuclei can be written as
where VN is nuclear potential and VC is Coulomb potential shown by 16
where Rc , the Coulomb radius, is
3. Results and Discussion
We have examined six versions of proximity potentials to describe the elastic scattering data of 13C + 12C, 13C + 16O, 13C + 28Si and 13C + 208Pb reactions. The distance-dependent variations of the potentials have been shown in Fig. 1. In this context, we have listed the values of W
0, r
w
and a
w
parameters of the imaginary potential in Tables I, II, and III. In Table IV, we have presented the cross sections (
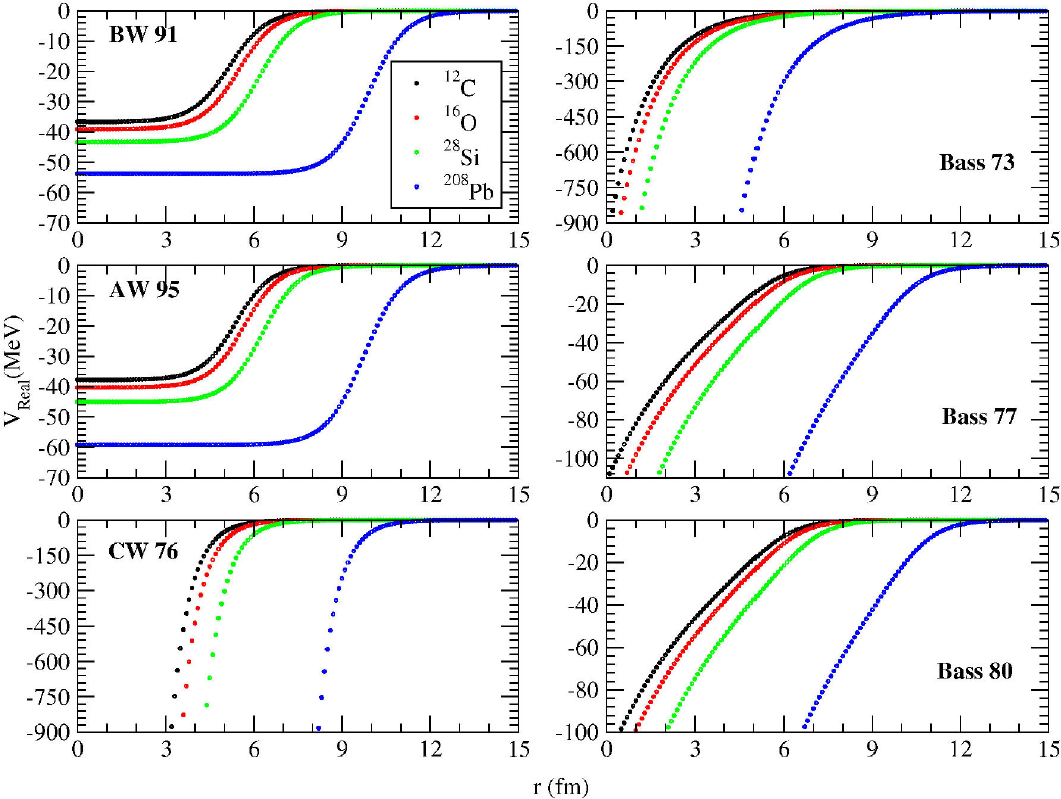
Figure 1. Distance-dependent changes of BW 91, AW 95, CW 76, Bass 73, Bass 77 and Bass 80 potentials.
Table I. The W0 values of the imaginary potential for the BW 91, AW 95, CW 76, Bass 73, Bass 77 and Bass 80 potentials used in the analysis of the 13C + 12C, 13C + 16O, 13C + 28Si and 13C + 208Pb systems.

The elastic scattering cross section of 13C + 12C reaction has been analyzed at incident energy of 250 MeV and the theoretical results have been showed in Fig. 2. It has been observed that there is amplitude difference between the results of the potentials with experimental data. It has been noticed that BW 91 and Bass 80 potentials have presented a similar behavior. However, it has been found that the results of CW 76 potential are slightly better than the results of the other potentials.
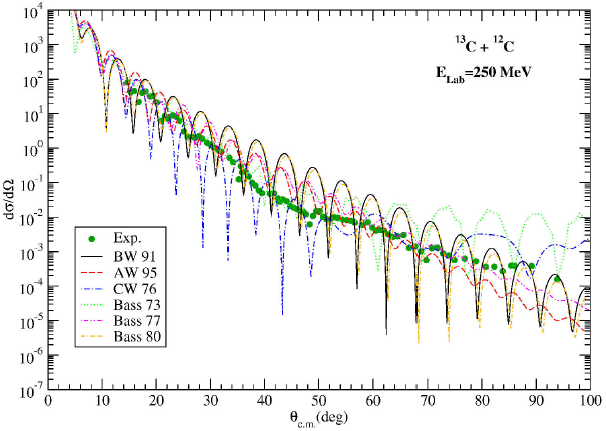
Figure 2. Comparison with the experimental data of the 13C + 12C elastic scattering cross sections for the BW 91, AW 95, CW 76, Bass 73, Bass 77 and Bass 80 potentials at Elab = 250 MeV. The experimental data have been taken from 18.
The angular distribution of 13C + 16O elastic scattering at 50 MeV has been calculated and plotted in Fig. 3. The results are very close together at backwards angles except for the Bass 73 potential. The worst results have been found for the Bass 73 potential. On the other hand, the best results have been obtained with the BW 91 potential.
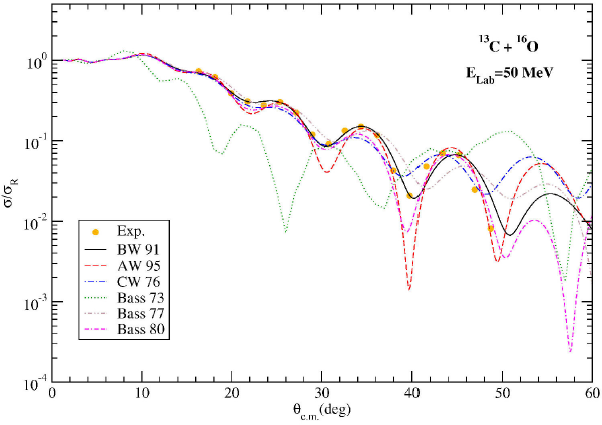
Figure 3. The same as Fig. 2, but for the 13C + 16O reaction at Elab = 50 MeV. The experimental data have been taken from 19.
Another reaction analyzed by using proximity potentials is 13C + 28Si at incident energy of 60 MeV. The elastic scattering results obtained under the OM have been presented in Fig. 4. When the results are compared to each other, the worst results have been found for the Bass 73 potential. However, the BW 91 potential has given slightly better results than the other potentials.
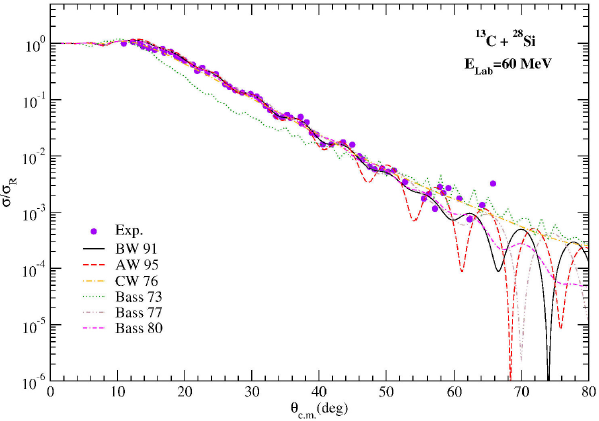
Figure 4. The same as Fig. 2, but for the 13C + 28Si reaction at Elab= 60 MeV. The experimental data have been taken from 20.
Finally, the elastic scattering data of 13C + 208Pb reaction have been examined via six different nuclear potentials at 390 MeV. The theoretical results have been plotted in Fig. 5. We have observed that the Bass 73 potential have given the worst results compared to the other potentials which are very similar to each other. Moreover, the Bass 77 potential has provided slightly better results than the other potentials.
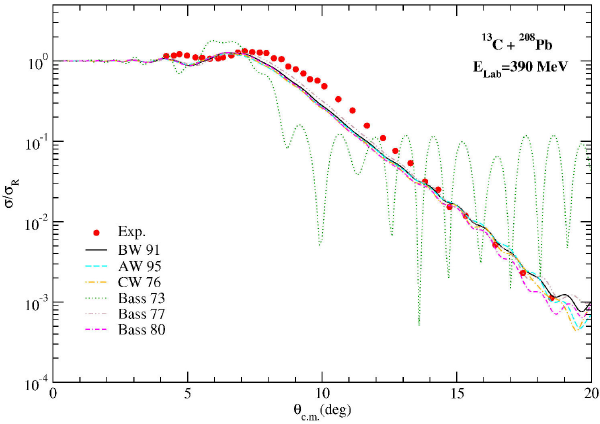
Figure 5. The same as Fig. 2, but for the 13C + 208Pb reaction at Elab= 390 MeV. The experimental data have been taken from 21.
When we examine the potentials that give the most consistent results with the experimental data for the four different reactions studied, the BW 91 type potential stands out significantly. This potential is basically the potential of the Woods-Saxon type, and the difference is only the method used to determine the potential parameters. It can be said that proximity potential similar to Woods-Saxon type within the scope of BW 91, AW 95, CW 76, Bass 73, Bass 77 and Bass 80 proximity potentials which are generally used to explain fusion reactions is more effective in describing the experimental data.
4. Summary
In this work, we have examined the applicability of proximity potentials to define the elastic scattering cross section. In this respect, we have studied six type proximity potentials to obtain the real part of the optical potential. We have used the WS potential for the imaginary part and have listed all the values of the potential in tables. Then, we have compared the theoretical results with each other as well as the experimental data. We have observed that the results of BW 91 potential are slightly better than the results of the other potentials in general sense. On the other hand, we have noticed that the Bass 73 potential has given the worst results compared to the other potentials. Thus, we have deduced that the theoretical results depend on the choice of the nuclear potentials used in the calculations. We can say that the potentials according to the shapes gives different results with each other and that the harmony with the experimental data increases or decreases.
Consequently, this work provides alternative potential ways to analyze the nuclear interactions. We think that it would be important and useful to investigate more different reactions by using this potentials.











 nueva página del texto (beta)
nueva página del texto (beta)





