Introducción

La precisión en el cálculo del volumen de madera en pie es indispensable para el aprovechamiento forestal sustentable, para lo cual se debe disponer de herramientas que permitan obtener tal información de un árbol o de la masa de forma rápida y confiable, mediante variables sencillas de medir como el diámetro normal (dn) o la altura total (h) (^{Barrio et al., 2004}).

La evolución de los rodales en sus características dasométricas resultantes del manejo silvícola, modifica de manera proporcional la forma de los árboles, la calidad de la madera y la distribución de sus productos (^{Uranga et al., 2015}), que están intrínsecamente relacionadas con las condiciones de los sitios, la densidad y la posición social de cada individuo (^{Harold y Hocker, 1984}). Por lo tanto, es importante la generación de nuevas tablas de volumen y factores de forma (ff) para evitar errores en la estimación de las existencias maderables, lo que altera los programas anuales de corta y, en general, la planeación y ejecución del manejo de los bosques (^{Carrillo et al., 2004}).

Un coeficiente mórfico o factor de forma se define como el cociente entre el volumen real del tronco y el volumen de un modelo que se toma como referencia y se distingue con la letra f; por su parte, un cociente de forma es la expresión entre dos diámetros medidos a alturas diferentes del tronco, un diámetro de referencia y otro a una altura superior, y se denotan con la letra k (^{Diéguez et al., 2003}; ^{Prodan et al., 1997}).

En la Comunidad Indígena de Nuevo San Juan Parangaricutiro, Michoacán, desde 1983 se ha aplicado el manejo silvícola al bosque, mismo que junto con otros factores han modificado las características de las masas arboladas a lo largo del tiempo, lo que a su vez ha impactado en la forma de los árboles y la distribución de sus productos, como en casos observados por ^{Van Laar y Akça (2007}), ^{Picard et al. (2012}) y ^{Uranga et al. (2015)}. Por lo citado, y debido a que autores como Santiago et al. (2013) señalan cambios en la producción y rendimiento de las masas forestales de acuerdo a la edad, se considera importante realizar nuevos estudios para calcular el volumen maderable con herramientas actualizadas. En virtud de la necesidad de contar con esta información, el objetivo del presente estudio fue evaluar la precisión de los coeficientes y cocientes de forma para la estimación del volumen del tronco de árboles en pie de Pinus montezumae Lamb., en bosques de la población referida.

Materiales y Métodos

Muestreo y toma de datos

Selección y tamaño de la muestra. Se eligieron árboles sanos, de fuste recto y limpio, que no estuvieran aislados ni a las orillas del rodal. Para conocer el intervalo de las categorías diamétricas existentes, se realizó un muestreo preliminar de la masa. En la literatura se sugiere utilizar de 23 a 229 árboles para obtener tablas locales y regionales o una ecuación de volumen, (^{Da Cunha y Guimarães, 2009}; ^{Honorato, 2011}). En este estudio se seleccionaron entre 8 y 16 árboles de cada categoría diamétrica, que se denominaron “árboles tipo”; se trabajó con un total de 245 ejemplares, de los cuales se consideraron 161 para generar una ecuación de volumen y 84 muestras para calcular los coeficientes y cocientes de forma.

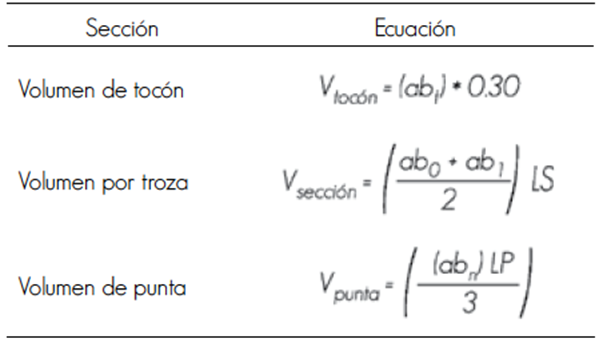
Medición de las variables. Los diámetros de la base, del tocón y a la altura de 1.3 m en el fuste se midieron con una forcípula (Haglöf Mantax Blue de 80 cm); la altura total y los diámetros a diferentes alturas, con el telerrelascopio de Bitterlich® (Pat. No. 172305). Los volúmenes por troza correspondientes a diferentes secciones del tronco se calcularon con la fórmula de Smalian, y la punta con la del cono (Cuadro 1). El volumen fustal (VFU), mediante la suma del volumen de todas las secciones del árbol.

Cuadro 1 Expresiones para el cálculo del volumen de las secciones del tronco. 

Donde:

ab _t = Área basal del tocón (m²)

ab ₀ = Área basal de la sección mayor (m²)

ab ₁ = Área basal de la sección menor (m²)

ab _n = Área de la base de la punta (m²)

LS = Longitud de troza o sección (m)

LP = Longitud de punta (m)

Cálculo de los coeficientes mórficos (f) y cocientes de forma (k)

Para facilitar la identificación de las partes de los árboles se denominó “tronco” al eje central del árbol y “fuste” a la longitud del eje hasta la punta delgada de 10 cm (^{Diéguez et al., 2003}). Con el volumen de cada individuo se determinaron los coeficientes mórficos y los cocientes de forma, con las ecuaciones indicadas en el Cuadro 2.

Cuadro 2 Ecuaciones y notación de los coeficientes y cocientes de forma evaluados para estimar el volumen de árboles en pie de Pinus montezumae Lamb. 

Análisis estadístico

Detección de datos atípicos. Con el paquete Statgraphics Centurion ^® y la opción “Mejorar-Análisis de regresión-Varios factores- Regresión múltiple” (^{Statpoint, 2005}), se detectaron los datos atípicos que influyeron negativamente en el ajuste de las ecuaciones. Se eliminaron las observaciones con residuos estudentizados > 2 en valor absoluto, con la expresión siguiente:

Si RStudent ≤ 2, evaluar si es mayor a 2 y en su caso eliminar la observación.

Cuadro 3 Modelos matemáticos empleados para estimar el volumen de Pinus montezumae Lamb. 

Análisis de correlación y regresión. Se ajustaron modelos matemáticos para predecir el volumen de los árboles en pie, con el paquete estadístico SAS v. 9 (^{SAS, 2009}). En el ajuste se emplearon los modelos de Schumacher-Hall, Thornber, Spurr con Variable Combinada Aritmética, Spurr con Variable Combinada Logarítmica y Korsun (Cuadro 3); se compararon los estadísticos: cuadrado medio del error (CME), Coeficiente de determinación ajustado (R2ajustado) y la significancia del modelo mediante F calculada y de los parámetros obtenidos. Además, se analizó de forma gráfica la dispersión de los residuales, la autocorrelación de los errores mediante la prueba de Durbin-Watson y la normalidad de los datos con la prueba de Shapiro-Wilk.

Los volúmenes calculados mediante la ecuación de mejor ajuste se contrastaron con los volúmenes obtenidos con cada uno de los coeficientes y/o cocientes de forma, y se evaluaron mediante las desviaciones expresadas en términos de la Diferencia Agregada (DA) en porcentaje. La regla de decisión planteada fue: el volumen determinado por los coeficientes y/o cocientes de forma con DA cercano a 1 % se pueden utilizar de modo confiable; asimismo, se consideró el intervalo y la desviación estándar de las observaciones. Con base en los trabajos de ^{Romahn et al. (1994}) y ^{Fonseca et al. (2009}), la expresión para la Desviación Agregada es:

Donde:

DA = Diferencia agregada en porcentaje

Σ Vc = Sumatoria de los volúmenes calculados

o estimados

Σ Vr = Sumatoria de los volúmenes reales

Resultados y Discusión

Tamaño de muestra. Para la ecuación de volumen, el tamaño final de la muestra después de eliminar los datos atípicos fue de 157 árboles y 84 para el cálculo de los coeficientes y cocientes de forma. Algunos autores emplean diferente número de muestras para la construcción de modelos de volumen, entre ellos ^{García et al. (2012)}, quienes para P. michoacana y P. michoacana var. cornuta Martínez emplearon 207 y 220 árboles, respectivamente; ^{Lores et al. (2010)} trabajaron con 23 muestras de Calophyllum brasilense Cambess, y ^{Montes de Oca et al. (2009)} con 124 árboles de Pinus duranguensis Martínez. La muestra utilizada para generar, tanto la ecuación de volumen como los factores de forma cumple para obtener resultados confiables.

Análisis de regresión y correlación. Los modelos de Schumacher- Hall y Thornber presentaron valores bajos en el CME. El valor de probabilidad es significativo (Pr ˂0001) para todos los modelos, además la explicación de la muestra, por ellos, es superior a 99 %. El análisis de regresión y los indicadores estadísticos de bondad de ajuste se muestran en el Cuadro 4.

Cuadro 4 Resumen de resultados de los estadísticos de cada modelo probado. 

GL = Grados de libertad; CME = Cuadrado medio del error.

Distribución gráfica de residuales. Se llevó a cabo el análisis de la distribución de los residuales de los mejores modelos, para determinar la no existencia de multicolinealidad; que los errores no estén correlacionados, que se distribuyan normalmente, y que el error tenga varianza uniforme (^{Alder, 1980}; ^{Velasco et al., 2007}; ^{Da Cunha y Guimarães, 2009}); además de examinar, visualmente, la forma de las relaciones y corroborar su homocedasticidad o heterocedasticidad (^{Prodan et al., 1997}). El análisis resultó sin tendencias (Figura 1).

Figura 1 Distribución de los residuales. 

Los modelos de Schumacher-Hall y de Thornber revelaron resultados estadísticos y gráficas de residuales similares; se prefirió el primero por la parsimonia del mismo, mayor facilidad de cálculo y por ser el más empleado en bosques de coníferas.

Validación del modelo Schumacher-Hall. En el Cuadro 5 se reúnen los estadísticos de Durbin-Watson y de Shapiro-Wilk, así como la significancia de los parámetros β₀, β₁ y β₂ del ajuste estadístico.

Cuadro 5 Estadísticos de validación del modelo de Schumacher-Hall 

El estadístico de Durbin-Watson (DW) señala que no existe autocorrelación de los errores, porque presenta un valor de 1.96, en el cual los residuos son independientes; el estadístico de Shapiro-Wilk, con 0.9951 indica que no se viola el supuesto de normalidad de los errores, ya que la probabilidad de rechazo es menor a 0.05 y es significativa (^{Martínez et al., 2006}; ^{Velasco et al., 2007}; ^{Da Cunha y Guimarães, 2009}); por lo que se asume que la muestra procede de una población que sigue una distribución normal; en el Cuadro 2 se observa que los coeficientes β₀, β₁ y β₂ son significativos (p>F = <0.0001). La ecuación generada con el modelo de Schumacher-Hall fue la siguiente:

V=0.0000584616 D^1.96205 H^0.93483

Evaluación de los coeficientes y cocientes de forma. Con el volumen de los 84 árboles destinados ex-professo para calcular los coeficientes y cocientes de interés, se obtuvo un promedio, cuyos resultados se listan en el Cuadro 6.

Cuadro 6 Valores promedio de los coeficientes y cocientes de forma. 

El valor del coeficiente mórfico del tronco varía entre 0 y 1, puesto que el volumen de cualquier tipo dendrométrico por si solo, o de una combinación de varios, es siempre menor o igual que el volumen del cilindro (^{Diéguez et al., 2003}). El valor obtenido en este estudio para Pinus montezumae fue de 0.525, sin embargo es superior al de ^{Uranga et al. (2015)}, cuya cifra se ubicó en el intervalo de 0.44 a 0.50 para P. patula Schiede ex Schltdl. & Cham. en tres regiones de México.

El coeficiente mórfico del fuste a la altura total es el más utilizado, cuando se pretende estimar el volumen fustal; el inconveniente es que su valor no tiene límite superior marcado; es decir, puede ser >1, porque se comparan los volúmenes de dos cuerpos de diferente altura, aunque en todo caso, siempre es < 1 para los tipos dendrométricos clásicos (^{Diéguez et al., 2003}); para P. montezumae el valor promedio fue de 0.557.

Para el coeficiente mórfico del fuste a la altura del fuste, se tiene la ventaja de que se contrastan los volúmenes de dos cuerpos de igual altura, por lo cual el valor límite superior = 1 (^{Diéguez et al., 2003}); el valor promedio en este estudio fue de 0.601.

El coeficiente mórfico referido a la sección basal apenas se utiliza, debido a las irregularidades propias de la base del tronco. Los correspondientes a las secciones fijas tienen el inconveniente de que para árboles de igual forma; esto es, para árboles que disminuyen en igual proporción a lo largo del eje longitudinal, pueden dar valores distintos y viceversa; para individuos con forma irregular es factible que tengan el mismo valor del coeficiente mórfico (^{Diéguez et al., 2003}). El promedio calculado para P. montezumae fue de 0.460.

Los factores de forma falsos no son cabalmente comparables, porque no permiten una representación directa de la forma geométrica del fuste debido a su referencia al d, y contienen un elemento distorsionante (^{Prodan et al., 1997}).

Dos árboles con la misma forma tienen igual coeficiente mórfico referido a una sección relativa (no fija); por lo tanto, son más descriptivos de su forma que los coeficientes mórficos artificiales. Los valores para los coeficientes de Hohendahl para los tipos dendrométricos clásicos fueron: cilindro (1), paraboloide (0.556), cono (0.41) y neiloide (0.343) (^{Diéguez et al., 2003}). Sobresale el método de Hohendahl porque conduce a un factor de forma natural, a través de la medición de dos diámetros del fuste siempre en términos relativos, o que permite ser comparable en cualquiera de las condiciones dimensionales del tronco. El resultado del promedio del coeficiente mórfico de Hohendahl para el tronco fue de 0.561, con el fuste a la altura total, 0.587 y el del fuste a la altura del mismo, 0.639; al contrastar estos tres valores con los sugeridos por el autor para los tipos dendrométricos mencionados anteriormente, la forma del tronco de P. montezumae se asemeja a un paraboloide.

Al aplicar la fórmula de Pressler para los tipos dendrométricos, los datos generados fueron los siguientes: paraboloide, 0.500; cono, 0.333 y neiloide, 0.247 (^{Diéguez et al., 2003}); el promedio en el presente trabajo es de 0.511, valor que confirma el tipo paraboloide del tronco de P. montezumae; en los primeros dos, se obtienen volúmenes exactos y en el caso del neiloide arroja valores ligeramente inferiores a los reales (98.6 %); sin embargo, se plantean dudas sobre su fiabilidad y aplicabilidad cuando se pasa del concepto de sólidos geométricos al de troncos reales de árboles (^{López, 2005}).

El inconveniente de los cocientes de Schiffel y Pollanchütz es que carecen de un valor límite superior, por lo que es posible rebasar la cifra = 1, ya que, si la altura del árbol es inferior a 2.06 m o de 4.33 m respectivamente, la parte en la que se mide el diámetro del numerador está por debajo de la altura normal, y por lo tanto, el cociente puede ser >1. La desventaja frente al factor de forma normal de Schiffel radica en que no aporta información sobre el volumen bajo el diámetro normal (^{Diéguez et al., 2003}). El promedio del cociente de forma de Schiffel obtenido para P. montezumae fue de 0.718. Los valores de los cocientes de forma de Pollanchütz para los tipos dendrométricos fueron: paraboloide, 0.882: cono, 0.788 y neiloide, 0.686; en el presente trabajo el promedio fue de 0.831, lo que confirma la forma del arbolado tipo paraboloide (^{Prodan et al., 1997}).

El cociente de forma de Johnson representa de manera más precisa la forma del tronco que el cociente de forma normal de Schiffel, el cual tiene un valor máximo de uno que se alcanza cuando la altura del árbol es de 1.30 m, y en la mayoría de las especies su valor varía entre 0.6 y 0.8. Los valores del cociente de forma de Johnson para los tipos dendrométricos son: paraboloide (0.707), neiloide (0.354), cono (0.500) (^{Diéguez et al., 2003}), el promedio obtenido fue de 0.736 para P. montezumae que está dentro del intervalo de dominio de este cociente. El promedio del cociente de forma de Gieruszinski es de 0.581 y resultó ser el de menor valor de todos los cocientes evaluados.

Con P. montezumae de la región, se pierde la sensibilidad de los cocientes de forma debido al paraboloidismo de los troncos, el cual es más acentuado en árboles jóvenes. Los cocientes de forma utilizados fueron los denominados “falsos”, que están referidos a una sección fija, los valores estimados fueron variados, ya que estos no están a un porcentaje de su altura total o maderable, con ello, se pierde la relación diámetro-altura.

Desviación agregada y Desviación estándar de los coeficientes mórficos

Desviación agregada (DA) y Desviación Estándar. El criterio de la DA establece que entre dos estimaciones no se debe exceder ± 1 % para mostrar una relación confiable (^{Romahn et al., 1994}; ^{Prodan, 1997}; ^{Fonseca et al., 2009}), en el presente caso es entre los valores volumétricos estimados y los obtenidos con los coeficientes y cocientes de forma. La desviación estándar es el promedio de las desviaciones de las observaciones, respecto a su media expresados en las mismas unidades de la medición (^{Caballero, 1972}); por lo que, el coeficiente o cociente de forma que registre el menor valor se ajustará más estrechamente al valor central y, por lo tanto, es más eficiente (cuadros 7 y 8).

Cuadro 7 Desviación Agregada (%) y Desviación Estándar de los coeficientes mórficos. 

Cuadro 8 Desviación Agregada y Desviación Estándar de los cocientes de forma. 

Con el coeficiente mórfico del tronco (0.52 %) y el coeficiente mórfico del fuste a la altura total (-0.85) se logró la premisa porcentual de ± 1%; el coeficiente obtenido con la fórmula de Pressler alcanzó un valor bastante aproximado a la unidad (1.18 %); y el resto de los coeficientes estuvieron entre 6.98 % (coeficiente mórfico para el fuste a la altura del fuste) y 15.18 % (coeficiente mórfico de Hohendahl para el fuste a la altura del fuste).

Los coeficientes con menor desviación estándar fueron el del fuste a la altura total (2.2013) y el de Pressler (2.2126); los más altos, el referido a la sección basal (3.0903) y el de Hohendahl del fuste a la altura del fuste (2.5631).

Desviación agregada (DA) y Desviación Estándar de los cocientes de forma

Los valores en DA obtenidos con los cocientes de forma fueron significativamente mayores que los mostrados con los coeficientes de forma ya que sus valores variaron de 28.22 % (Schiffel) a 43.42 % (Zimmerle).

La desviación estándar de los cocientes de forma que presentaron menor porcentaje fueron el de Johnson, Schiffel y Pollanschütz; los mayores fueron el Zimmerle y Gieruszinski. Aun cuando los coeficientes y cocientes de forma que utilizan el fuste en punta delgada tienen valores similares a los sugeridos por sus autores, es probable que su precisión aumente si el diámetro en punta delgada también lo hace de 10 a 20 cm o más, lo que puede variar con el tipo dendrométrico que mejor reprente al tronco de una especie en particular.

De todos los coeficientes y cocientes de forma, solamente tres lograron la precisión requerida para hacer estimaciones confiables del volumen de árboles en pie: el coeficiente mórfico del tronco y el coeficiente mórfico del fuste a la altura total, así como el coeficiente obtenido con la modificación en la fórmula de Pressler.

Comparación de los volúmenes calculados con la ecuación de volumen y los coeficientes de forma

En la Figura 2, se presentan las gráficas que ilustran la relación entre los volúmenes obtenidos con el modelo de Schumacher - Hall y los generados con los mejores coeficientes de forma.

Figura 2 Comparación entre los volúmenes de los coeficientes y cocientes de forma y los de la ecuación de volumen. A. Coeficiente mórfico del tronco, B. Coeficiente mórfico a la altura total, C. Coeficiente mórfico de Pressler, D. Coeficiente mórfico de Hohendahl para el tronco y E. Coeficiente mórfico de Hohendahl para el fuste a la altura total. 

En los tres primeros casos existe una amplia coincidencia entre los valores estimados con la ecuación de volumen y los obtenidos con los coeficientes indicados, lo que demuestra la factibilidad de usarlos con confianza para la estimación del volumen de árboles en pie de P. montezumae que crecen en los bosques de la Comunidad Indígena de Nuevo San Juan Parangaricutiro, Michoacán. Los valores de los coeficientes mórficos de Hohendahl para el tronco y para el fuste sobreestiman los volúmenes, a partir de la categoría diamétrica de 20 cm y de 50 cm, respectivamente.

Conclusiones

Los coeficientes mórficos y los cocientes de forma son una herramienta indispensable para una estimación rápida y precisa del volumen de árboles en pie y el empleo de alguno de ellos depende de la estructura de los troncos de las especies bajo evaluación. Los cocientes estiman mejor las conformaciones cónicas y neiloidicas y los coeficientes se asocian mejor a las paraboloides. Además, representan una alternativa para la construcción de tablas o tarifas de volumen comercial en los individuos de esta especie.

Los coeficientes de forma falsos presentaron la ventaja de estimar con mayor precisión el volumen debido al paraboloidismo de los troncos de Pinus montezumae, mientras que los verdaderos utilizan un diámetro de referencia en relación con la altura total del árbol que para ser más precisos necesitan un ahusamiento más agudo que el que tiene P. montezumae.

Los valores promedio que se obtuvieron con los coeficientes mórficos de Hohendahl para el tronco y para el fuste a la altura total, se ubican dentro de los intervalos sugeridos por el mismo autor para el tipo dentrométrico paraboloide (0.566); sin embargo, al compararlos con los volúmenes reales se reconoce una sobreestimación.

Los coeficientes mórficos del tronco, del fuste a la altura total y el coeficiente mórfico de Pressler, fueron los que presentaron menores desviaciones entre los volúmenes estimados y los calculados, por lo que su uso es confiable en la estimación volumétrica del tronco de árboles de Pinus montezumae.

A partir de los resultados obtenidos, se concluye que es posible la predicción de la forma y volumen del tronco de Pinus montezumae, mediante los coeficientes mórficos y cocientes de forma que resultó en una forma paraboloide.

Conflicto de intereses

Los autores declaran no tener conflicto de intereses.

Contribución por autor

Guadalupe Geraldine García Espinoza: diseño de la investigación, toma de datos de campo, redacción y estructura del documento; José Jesús García Magaña: planeación, diseño y supervisión del trabajo de campo, redacción y estructura del documento, Jonathan Hernández Ramos: captura y análisis de la información y redacción del documento; Hipólito Jesús Muñoz Flores: capacitación en el manejo del Telerrelascopio de Bitterlich y revisión del documento; Xavier García Cuevas: asesoría estadística y revisión del documento; Adrián Hernández Ramos: procesamiento de los datos de campo y revisión del documento.