Introduction
In arid and semiarid mountain regions, the cryosphere is the principal water supply and the most vulnerable to climate change as the ice is a source of natural storage during the summer and/or dry season (Karimi, Farajzadeh, Moridnejad, & Namdari, 2014; Milana & Maturano, 1999; Rabatel et al., 2008). In fact, rock glaciers are essential for hydrologic sources because they have more water than glaciers that retain frozen water between 29°S and 32°S (Azócar & Brenning, 2010). Moreover, the principal water provider to streamflow in mountainous regions is the snowmelt process (Favier, Falvey, Rabatel, Praderio, & López, 2009). However, during a drought, glaciers and permafrost can be the main source to summer streamflow and aquifer recharge (Favier et al., 2009; Milana & Güell, 2008).
In this context, several studies have shown glacier retreat in the previous decades (Bolch, 2007; Le Quesne, Acuña, Boninsegna, Rivera, & Barichivich, 2009; Rivera, Acuña, Casassa, & Bown, 2002). This phenomenon results in increasing runoff and a reduction of water infiltration. Hence, glacier melt studies are essential in water resources research (Rignot, Rivera, & Casassa, 2003; Rivera, Casassa, Acuna, & Lange, 2000). In fact, glacier and permafrost meltwater input to streamflow is little researched and often misunderstood (Pourrier, Jourde, Kinnard, Gascoin, & Monnier, 2014). Even more, Rabatel, Castebrunet, Favier, Nicholson and Kinnard (2011) mentioned that models and mass balance studies, which explain runoff patterns, do not exist for sub-tropical region.
On the other hand, runoff and snowpack are highly affected by precipitation changes (Yao, Liu, Huang, Liu, & Wu, 2014). Likewise, and in the presence of climate change, it would be expected that in the absence of changes in precipitation and with increasing temperature (Pizarro et al., 2013; Valdés-Pineda et al., 2014) runoff should have increased in the last several decades. Another factor that should affect the snowpack and glacier is the zero degree isotherm (ZDI). The ZDI is being modified by global warming (Valdes-Pineda et al., 2014), because the air is warmer. Moreover, the same study showed that the ZDI line has been rising since the 1980 ́s at a rate of almost 2.5 m every ten years, denoting a quick change in the environment. In the same context, Carrasco, Casassa and Quintana (2005), and Carrasco, Osorio and Casassa (2008) had studied the ZDI in Chile and they have concluded an increase in the ZDI in the wake of increasing temperature. Demaria, Maurer, Thrasher, Vicuña and Meza (2013) forecasted in the future with mathematical modelling that the precipitation in Chile may drop between 7-20%, i.e. less snow and less streamflow.
Some studies have related hydroclimatic factors such as runoff and/or precipitation to glacier-fed river flows (Baraer et al., 2012; Birsan, Molnar, Burlando, & Pfaundler, 2005; Kong & Pang, 2014; Liu, Wang, Gong, & Uygen, 2012; Pellicciotti, Bauder, & Parola, 2010; Sharif, Archer, Fowler, & Forsythe, 2013; Souvignet, Oyarzún, Verbist, Gaese, & Heinrich, 2012; Jiang, Zhou, & Cheng, 2007; Yao et al., 2014;). Moreover, these studies have a common factor in the methodology; all have used the Mann-Kendall trend test (MK). For example, Birsan et al. (2005) analyzed 48 watersheds in Switzerland and found a positive trend in annual streamflow. Yao et al. (2014) discovered an important glacial retreat in the Yangtze River in China and that just less than 20% of rainfall was transformed into runoff in the study basin. Despite the different objectives and data used in these studies, all of them concluded that mountainous basins are one of the most sensitive places to climate change and especially sensitive are basins with glaciers. Moreover and related with the glacier response to the meteorological data, Yamaguchi and Fujita (2013) found that in general the glaciers depend mostly on the precipitation pattern such as seasonality and amount.
Souvignet et al. (2012) studied the meteorological trend in northern Chile and they found a positive trend in summer temperature at high altitudes, a related with a decrease in rainfall in a long-term analysis the higher temperatures could explain glacial retreat within the study zone.
Other researchers have studied the contributions of glacier melt into the streamflow, for example, Hirose and Marshall (2013) in British Columbia, Howat, Tulaczyk, Rhodes, Isreal and Snyder (2006) in California, Singh and Kumar (1997) on the Himalayas, Ye et al. (2005) in China, among others.
A severe water availability gap affects northern Chile, but Chile is considered one of the Latin American countries with the highest water volume available (DGA, 1999). According to the Valdés-Pineda et al. (2014) study, the average water availability in Chile is 53 953 m3 hab-1 yr-1 and the worldwide water availability is 6 600 m3 hab-1 yr-1. However, from Santiago to the north of Chile, the availability is less than 800 m3 hab-1 yr-1, and the Coquimbo Region has 1 020 m3 hab-1 yr-1.
The goal of the present study is to analyze, statistically and mathematically, the temporal precipitation and runoff patterns to determine if glacier retreat is affecting streamflow in the Elqui River watershed, Coquimbo Region, in Northern Chile. This hypothesis is based on the following facts: (1) glacier retreat has generated increased runoff but with little data available to confirm, (2) runoff and snowpack are highly affected by precipitation changes and, with climate change, it would be expected that in the absence of changes in precipitation and with increasing temperatures, runoff should have increased or been maintained in the last several decades, and (3) the ZDI is being modified by global warming in response to increasing temperatures.
Methods
Study area
The Coquimbo Region has 7.02 km2 of covered glacier surface and the Tapado glacier, the high-light of the Region, is located in the Elqui river´s headwaters. It lies near 30° 08’ S and 69° 55’ W with an altitude of 5 200 masl (meters above sea level). It has an area of 3.6 km2, which represents an important part of the entire area covered by glaciers in the region (Oyarzun, 1987; Rivera et al., 2000).
The Elqui River watershed, located in the Coquimbo Region, lies near latitudes 29° 02’ S and 32° 34’ S and longitudes 71° 22’ W and 69° 52’ W (figure 1). It has an area of 9 656 Km2 and has a mixed hydrologic regimen (snow and precipitation). However, according to Young et al. (2010), the principal water sources to the Elqui river streamflow are snowmelt and glacier melt. Climatically, it is in the boundary between the desert climate of northern Chile and the semiarid climate of central Chile (Cabezas, Cepeda, & Bodini, 2007).
Data acquisition
This study is based on the monthly and annual precipitation data from four rain gauges and runoff records from 4 river gauging stations of the Elqui river watershed (figure 1 and table 1). The elevation of runoff gauging stations range between 860 masl (meters above sea level) and 3 130 masl, and the elevations of rain gauges range between 1 560 masl and 3 130 masl. The area of the sub-basin under study ranges between 222 km2 and 3 572 km2. The analysis was performed on the data recorded between 1970 and 2009. The required data was facilitated by the Chilean national water management institution (DGA, 1999), Coquimbo Region.
Table 1 Rain gauge and runoff station basic information.
| Rain Gauges | ||||||
| ID | Station |
Altitude (masl) |
Latitude | Longitude | Period | |
| 1 | La Laguna Embalse | 3 100 | 30° 12’ S | 70° 02’ W | 1970-2009 | |
| 2 | Juntas | 2 155 | 29° 58’ S | 70° 06’ W | 1970-2009 | |
| 3 | Los Nichos | 1 350 | 30° 09’ S | 70° 30’ W | 1970-2009 | |
| 4 | Rivadavia | 850 | 29° 58’ S | 70° 34’ W | 1970-2009 | |
| Runoff Stations | ||||||
| ID | Station |
Altitude (m.a.s.l.) |
Latitude | Longitude |
Sub-basin area (km2) |
Period |
| A | Rio la Laguna in Embalse La Laguna exit | 3 130 | 30° 12’ S | 70° 02’ W | 560 | 1970-2009 |
| B | Rio Toro before Junta Rio La Laguna | 2 150 | 29° 58’ S | 70° 06’ W | 468 | 1970-2009 |
| C | Rio Cochiguaz in El Peñon | 1 360 | 30° 07’ S | 70° 26’ W | 673 | 1970-2009 |
| D | Rio Turbio in Varillar | 860 | 29° 57’ S | 70° 32’ W | 4 148 | 1970-2009 |
Data analysis
First, the precipitation and flow data presented discontinuous information across the study period 1970-2009. In those cases, it was necessary to complete the missing data from each station using simple linear regressions, multiple regressions and historic averages (Pizarro-Tapia, Cabrera-Jofre, Morales-Calderón, & Flores-Villanelo, 2011; UNESCO, 1982). However, multiple regressions did not get better results than linear regressions.
Second, the area of influence of rainfall stations was estimated using the Thiessen Polygon method which representatively weights the rainfall depending on the surface (Pizarro-Tapia et al., 2011; Yao et al., 2014; Wada, Chikita, Kim, & Kudo, 2011). For this processing procedure, the digital topographic data of the study area was used.
Rainfall and flow data were grouped into four periods (1970-1980, 1970-1990, 1970-2000, and 1970-2009) to observe trends in the data over time by making an intercessional comparison and for the adjustment of the Probability Density Functions (PDFs) used. Then, 20, 50, and 75 year return periods were used to calculate the probability of exceedance for each PDF.
In this study Gumbel
To contrast these above results it was necessary to use a strong statistical test to probe the hypothesis that links precipitation and runoff patterns to possible glacier retreat. In this context, the idea to find a trend in the precipitation and discharge data is essential. Hence, one of the most widely used tools to detect trends in the data is the Mann-Kendall test (MK) (Hamed, 2008; Kendall, 1948; Mann, 1945; Song, Jiang, Lei, Wang, & Shu, 2015). This nonparametric test has been used by a larger number of researcher from multiple fields such as hydrology, geo-chemistry, human behavior, ecology, medicine among others. Thus, trend test assesses whether a time-ordered dataset exhibits an increasing or decreasing trend, within a predetermined level of significance. The null hypothesis of the MK trend test is H0 = t = 0 and the alternative hypothesis is H1= t≠ 0. According to this, the MK will be used over annual and monthly (seasonal) data (areal precipitation and specific discharge) to verify if the thawing of the permafrost is responsible for the increasing or maintaining summer flows and inferred disconnections of precipitation and flow.
Results and discussion
We have analyzed each sub-basin individually on a monthly and annual basis. However and because PDF fitting was not possible, an overall overview of the data at each basin on an annual basis was performed
Mean areal rainfall
Using Thiessen polygons method, the area of influence of each rainfall station was associated with the sub-basins defined by the gaging stations in Rio Turbio en Varillar henceforth Rio Turbio; Rio Cochiguaz en El Peñon, henceforth Rio Cochiguaz; Rio la Laguna on departure Embalse La Laguna, henceforth Rio La Laguna; Rio Toro, formerly Junta Rio; La Laguna, henceforth Rio Toro (table 2). The mean areal rainfall for the sub-basins in the study was determined by weighted averages of the surfaces.
Table 2 Surfaces defined by the method of Thiessen polygons for each sub-basin.
| Sub-basin | Rio Turbio | Rio Cochiguaz | Rio La Laguna | Rio Toro |
| Rain gauge station | Surface (km2) | |||
| Rivadavia | 1 290.6959 | - | - | - |
| Los Nichos | 37.7941 | 361.0911 | - | - |
| La Laguna Embalse | 631.3946 | 197.7601 | 221.8748 | - |
| Juntas | 1 611.7806 | - | - | 615.7333 |
| Total Basin surface | 3 671.6652 | 558.8512 | 221.8748 | 615.7333 |
PDF fitting for monthly/annual flows and rainfall
The Gumbel (EV1) function does not fit the four sub-periods of study and for this reason, Log-Normal, Pearson III, and Goodrich functions were used to fit the data. The following results do not consider Pearson III because it did not provide better results. For a return period of 50 years, Rio Turbio and Rio Cochiguaz for all the periods Log-Normal PDF was used; for Rio La and Rio Toro for the four period analyzed, a Goodrich PDF was used.
Rainfall fit
The variability of precipitation data did not permit adjustment periods as was the case for flow data fit; therefore, the adjustment was made monthly, with probability distribution functions of Gumbel, Log-Normal, and Goodrich. However, there were months where the PDF could not adjust. As a result the PDF that was used for a return period T = 50 years.
To interpret the behavior of rainfall and flows in the recent decades and because the PDF fit was not possible at this time, on figure 2 the temporal variation and susceptibility data is represented by a trend line with the corresponding equation from both variables on an annual basis for the whole period 1970-2009.

Figure 2 Annual amount (mm) for precipitation (grey squares) vs. flow (black triangles), on the four sub-basins analyzed were: a) Rio Turbio, b) Rio Cochihuaz, c) Rio La Laguna, and d) Rio Toro.
In the case of the Rio Turbio and Rio Toro sub-basin, there is more rainfall than flow, a logical situation if hypothesized that flows originate from precipitation. Furthermore, trends in both variables are presented as a relatively stable pattern. Also, there is greater variability in the precipitation than the streamflow in both sub-basins; this can be ratified by calculating the coefficient of variation (CV) of both variables. For precipitation at Rio Turbio sub-basin, the CV is 71.20% and 62.32% for streamflow and at Rio Toro sub-basin the precipitation’s CV is 75.53% and 37.25% for the flow.
For the Rio Cochiguaz sub-basin, there is no difference between the precipitation and the flow. It is clear that in this sub-basin the flow has a slightly decreasing trend; meanwhile the precipitation shows the contrary. At Rio La Laguna sub-basin, precipitation amount does not exceed the flow which also has a decreasing trend. This decrease could be due to low water reserves in the form of ice and snow in the basin. Also, there is greater variability in precipitation than inflow, which can be verified by calculating the coefficient of variation (CV) of both variables. The precipitation’s CV is 67.49% and the flow’s CV is 51.23%.
PP Q-1 coefficient: annual analysis
Figure 3 shows variability through the years of study where annual rainfall generally exceeds flows. However, there are moments in which this pattern is not true, PP Q-1 is less than 1 and flow exceeds precipitation. This result could be due to the lack of stations in the upper area of the basins, which would enable them to make a better estimate of the contributions of precipitation in liquid or solid form. The Rio La Laguna sub-basin in general has annual flows that exceed precipitation, but there are years where this does not occur. The year 2000-2001 in particular draws attention as it reaches a value of 2.6 on PP Q-1 coefficient, product of very low annual flow in that year. If this data is removed from the graph, the ratio would have a negative trend like the previous sub-basins. Despite this particular behavior for the 2000-2001 period, this sub-basin is one of the most important within the rest analyzed because the Tapado Glacier is located in the headwater.
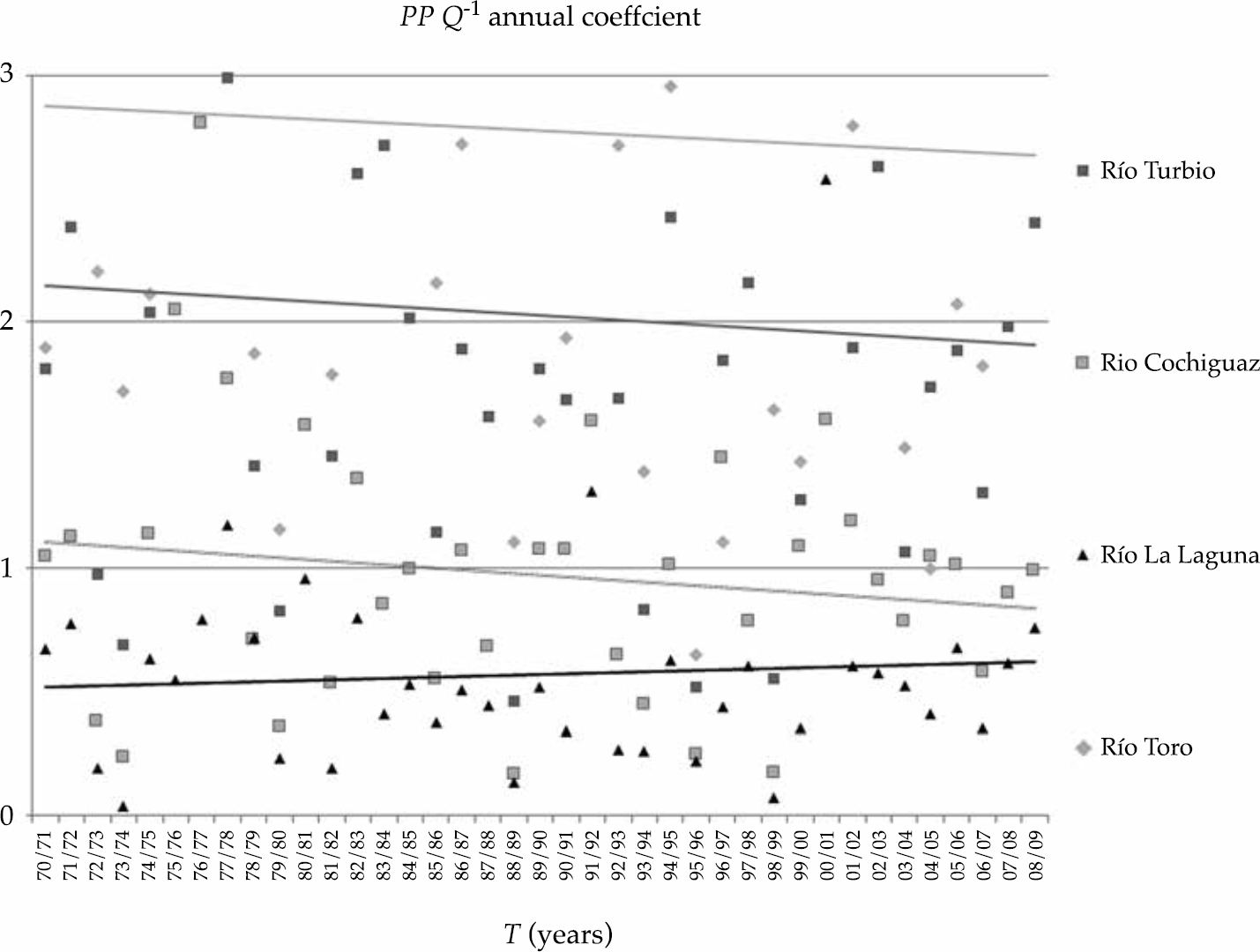
Figure 3 Graph of behavior of the PP Q-1 ratio yearly in the Rio Turbio, Rio Cochiguaz, Rio La Laguna, and Rio Toro sub-basins.
What is clear is that the PP Q-1 ratio tends to decrease which may be caused by two reasons. First, precipitation has decreased and flows have remained constant or on the other hand, precipitations have been steady and flows have increased. In both cases, there is speculation that there are contributions from glacier melt. Thus, on an annual basis it can be seen that the runoff is the same or it has increased despite decreasing precipitation.
In the 1995-1996 hydrological year, the PP Q-1 coefficient was less than 1 in the four sub-basins and flows are generally in proportion to the rainfall. This situation means that it is facing a year of drought where glaciers may be supplying significant water to the stream. This situation was repeated in the years 1973-1974, 1979-1980, 1988-1989, 1993-1994, 1995-1996, and 1998-1999 in Rio Turbio, Rio Cochiguaz, and Rio La Laguna River sub-basins. However and again, Rio La Laguna has special importance due to the presence of the Tapado Glacier.
PP Q-1 coefficient: summer versus winter
Mean areal precipitation and average flow for monthly-level data are presented (table 3) to summarize if rainfall exceeded the flow or not. The slopes represent the tendency of the precipitation or flow to decrease or increase over time. Thus, if the precipitation/flow slope is greater than zero that means that it has a positive trend in time. Otherwise, the trend is negative.
Table 3 Slope of the trend line for precipitation (m PP), flows (m Q), and PP Q-1 trend.
| Month | Sub-basin | |||||||||||
| Rio Turbio | Rio Cochiguaz | Rio La Laguna | Rio Toro | |||||||||
| m PP | m Q |
PP
Q-1 Trend |
m PP | m Q |
PP
Q-1 Trend |
m PP | m Q |
PP
Q-1 Trend |
m PP | m Q |
PP
Q-1 Trend |
|
| Apr | -0.061 | -0.006 | PP > Q | -0.057 | -0.056 | PP < Q | 0.010 | -0.064 | PP < Q | -0.139 | -0.004 | PP > Q |
| May | 0.216 | -0.004 | PP > Q | 0.342 | 0.005 | PP > Q | 0.213 | 0.041 | PP > Q | 0.231 | 0.003 | PP > Q |
| Jun | 0.279 | -0.002 | PP > Q | 0.266 | 0.049 | PP > Q | 0.015 | 0.068 | PP > Q | 0.411 | 0.005 | PP > Q |
| Jul | -0.298 | -0.007 | PP > Q | -0.718 | 0.051 | PP > Q | -0.635 | 0.060 | PP > Q | -0.050 | 0.004 | PP > Q |
| Aug | 0.171 | 0.002 | PP > Q | 0.309 | 0.055 | PP > Q | 0.437 | 0.109 | PP > Q | -0.039 | 0.005 | PP > Q |
| Sep | -0.030 | -0.002 | PP > Q | -0.007 | 0.066 | PP < Q | -0.011 | -0.284 | PP < Q | -0.030 | 0.006 | PP > Q |
| Oct | -0.114 | -0.031 | PP < Q | -0.113 | 0.012 | PP < Q | -0.187 | -0.453 | PP < Q | -0.126 | 0.009 | PP < Q |
| Nov | -0.026 | -0.026 | PP < Q | 0.010 | 0.027 | PP < Q | 0.056 | -0.233 | PP < Q | -0.066 | 0.009 | PP < Q |
| Dec | -0.027 | -0.020 | PP < Q | 0.007 | -0.053 | PP < Q | 0.022 | -0.192 | PP < Q | -0.070 | -0.021 | PP < Q |
| Jan | -0.046 | -0.023 | PP < Q | -0.018 | -0.225 | PP < Q | -0.030 | -0.187 | PP < Q | -0.088 | 0.019 | PP < Q |
| Feb | -0.026 | -0.054 | PP < Q | -0.016 | -0.303 | PP < Q | -0.040 | -0.166 | PP < Q | -0.029 | -0.037 | PP < Q |
| Mar | 0.002 | -0.006 | PP < Q | 0.011 | -0.277 | PP < Q | 0.021 | -0.378 | PP < Q | -0.023 | -0.034 | PP > Q |
| Total | 0.040 | -0.239 | PP > Q | 0.015 | -0.668 | PP < Q | -0.130 | -1.682 | PP < Q | -0.016 | -0.078 | PP > Q |
First, it can be seen that the flows are greater than the rainfall values in the spring/summer months, that is, between October and February flows were not produced from rainfall. On an annual basis, it is seen that the flow rates tend to decrease more strongly than the rainfall in all sub-basins. However, in the Rio Turbio and Rio Cochiguaz sub-basins, annual precipitations show a slight increasing trend. This trend in both Rio Turbio and Rio Cochiguaz, the highest sub-basin analyzed, might be due to the rise of the ZDI line where it has modified precipitation behavior (i.e. What was once snow is now rain).
Flows exceed precipitation values in summer months. Some proportion of this behavior could be explained by melt processes (late September and early October). However, from December to February, the snowmelt flows were still proportionally greater than the precipitation.
Furthermore, the precipitation data does not explain the flow pattern solely. It is shown that the precipitation in all sub-basins tend to decline whereas flow tends to increase or remain constant. It seemed to be that the water supply comes from snow or ice melt, since it is clear the precipitation is not feeding streamflow at least in summer time.
By the high variability of the PP Q-1 coefficient value, a trend analysis for two summer months and two winter months was performed. First, the summer months (figure 4) have very few occasions where the values of the PP Q-1 ratio exceed 1 which infers that rainfall rarely exceeded the value of flows. For summer drought months it is also important to highlight the trend in the months of low water for the PP Q-1 ratio, which is mostly negative over time, which would indicate that the flows have tended to grow more than precipitation and can be attributed to a change in temperatures and a higher incidence of glacier melt and snowmelt.
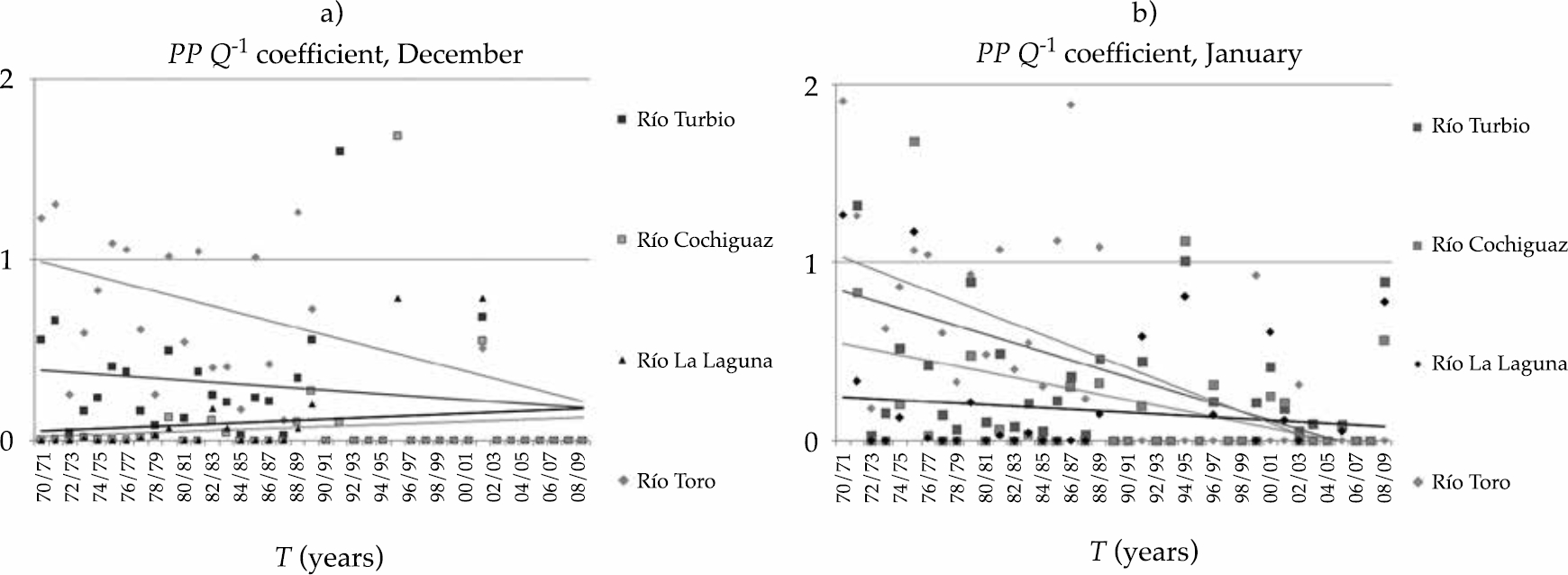
Figure 4 Graphic of the behavior of the PP Q-1 coefficient for December (a) and January (b) in the Rio Turbio, Rio Cochiguaz, Rio La Laguna and Rio Toro sub-basins.
Precipitation behavior does not match with the flow pattern. The PP Q-1 coefficient for the wet months generally exceeds 1 which means that precipitation was greater than flow. There are also values that did not surpass the value 1 which were associated with dry years. In general terms, there are differences between the behavior of the summer months and the winter months since the summer months seem to express themselves with less-than-normal rainfall, which would accelerate the snow and glacial melting processes that fill the water deficit in the sub-basins in the study.
MK trend test
The MK test did not find significant changes in the streamflow amount, but a negative trend was found in precipitation during the dry season (summer). These results were performed using the areal precipitations and average flow (specific) annually and monthly between 1970 and 2009 in the four sub-basins studied. On table 4, a negative sign in front of the bracket means a decreasing trend and a positive sign means an increasing trend in both discharge and precipitation.
Table 4 MK monthly trend test summary, 4 period, 4 sub-basins.
| 1970-2009 | 1970-2000 | 1970-1990 | 1970-1980 | ||
| Rio Turbio | Q Trend | No Trend | No Trend | No Trend | No Trend |
| PP Trend | -[Sep-Feb] | -[Oct-Feb] | -[Nov/Jan] | -[Jun] | |
| Rio Cochiguaz | Q Trend | +[Jun] | No Trend | No Trend | No Trend |
| PP Trend | -[Oct-Dec] | -[Oct-Nov] | -[Jun/Nov/Jan] | No Trend | |
| Rio La Laguna | Q Trend | No Trend | No Trend | +[Jun] | No Trend |
| PP Trend | No Trend | No Trend | No Trend | +[Jul/Oct] | |
| Rio Toro | Q Trend | No Trend | No Trend | No Trend | No Trend |
| PP Trend | -[Apr/Sep-Mar] | -[Apr/Sep-Feb] | -[Apr/Jun/Sep-Mar] | -[Jan] | |
In each of the four sub-basins, the 1970-1980 period does not present a trend in the flow data. This pattern could be possibly caused by the temperatures that were constant or rising in time or the effect of the rise of the ZDI is not evidenced yet.
On an annual basis, Rio La Laguna sub-basin in the 1970-1980 period (not showed) shown a positive precipitation trend. Nevertheless, this sub-basin does not have many changes in flow/precipitation.
For the Rio Turbio and Rio Cochiguaz sub-basins, the average flow does not present any trend in the four periods analyzed both annually and monthly. On the other side, precipitation shows a specific pattern, especially in the summertime where negatives trends in the precipitation pattern was found. Contrasting this and according by Favier et al. (2009), who have investigated precipitation and flow patterns within the Coquimbo region, they have found an increasing trend inflows and a nearly constant trend in mean precipitation.
Rio La Laguna sub-basin does not illustrate any decreasing tendency in either flow or precipitation. A contradictory situation occurs at this station because it shows a tendency for a decreasing PP Q-1 coefficient. According to Favier et al. (2009), over the 3 000 m line above sea level, the principal water supply is snow melt. In this sense, in Rio La Laguna sub-basin which is above 3 000 m, summer water came from snow/ice melt. This no trend could be explained because at this altitude no evidence exists about how water supply behaves between the gauge station and the Tapado Glacier (upstream). In fact, Monnier, Kinnard, Surazakov and Bossy (2014) have found an important retreat of the Tapado Glacier between 1956 and 2010 with a retreat distance closer to 400 meters. Also, at this elevation and in the winter months, the measured water in the rain gauge could be melted snow, and measurement error at this station could be an issue.
Similar relationships occur in the Rio Toro sub-basin (table 4) where no trend in flow was found. The longer periods (except in October) are the ones with the largest decreases in monthly flow. It is important to mention that this sub-basin comes from the Rio La Laguna sub-basin. Because the Rio La Laguna sub-basin does not present any trend, it is highly probable that the Rio La Laguna sub-basin directly influences the flow behavior of the Rio Toro sub-basin.
Another reason that supports the fact that the rivers are fed with water from melting snow and ice, is the Valdes-Pineda et al. (2014) study, who found strong evidence of the decline of the water table in the region of Coquimbo.
A simple tendency analysis over the average temperatures (1974-2009) in Rio La Laguna station show for the annual analysis and for the winter months especially on June, July and August that the temperatures are increasing. The same analysis was performed using a seasonal MK test which found the same behavior and these results match with the findings made it by Souvignet et al. (2012).
Comments and conclusions
The PP Q-1 ratio manifested high variability in all the sub-basins in this analysis, but it also manifests a clear declining trend in the months of dry season due to flows exceeding precipitation. The flows have been maintained even though precipitation decline shave been observed. These conditions indicate that contributions from a glacier retreat are the best explanation for observed streamflow. This result matches with the Souvignet et al. (2012) study which found similar results correlated with a negative trend in precipitation and a no trend in the discharge, which could be explained by a glacial retreat too. For instance, Vicuña, Garreaud and McPhee (2011) modeling future scenarios for the Limari watershed, the closest neighbor of Elqui watershed, showed increased temperatures and decreased precipitation, which will affect direct the hydrological behavior of the watershed and especially the permafrost and snow present at high altitudes.
For each winter month there is a clear increase of rainfall, exceeding the flows, while in the dry months is evidence of maintenance of the flows related to the decline in rainfall, which would only be attributed to a greater snow/ice melt. In this same track, Favier et al. (2009) found the same relation between flow and precipitation, concluding that snow/ice melting strongly influence the water supply.
It is clear through the MK tests that stream-flow in the 4 sub-basins have not undergone significant changes in their amounts. It is also clear that a negative trend in rainfall during dry periods (summer time) would explain where the water comes to maintain the flow in each of the sub-basins studied. In this context and for the known effect of climate change in Chile (Demaria et al., 2013; Pellicciotti, Ragettli, Carenzo, & McPhee, 2014), it is highly likely that the increase in temperature is causing the headwater glacier in the Elqui catchment to experience melting. This change also affects the snow cover due to the rise of the ZDI (e.g. Demaria et al., 2013). This directly affects surface runoff and aquifer recharge which depends heavily on snow reserves and the process of meltwater infiltration into the soil (and soil frost control).











 nueva página del texto (beta)
nueva página del texto (beta)



