Introduction
Aquaculture is a fast-growing sector with a worldwide fish production of 80 MT in 2016, which represents 88 % with regard to worldwide fisheries production, calculated to be 90.9 MT for the same year (FAO, 2018). Tilapia is a popular fish in the world freshwater aquaculture with 126 reported countries or regions, in which a production of 5.7 MT was recorded in 2015, according to data from FAO (2016). A relevant goal to keep this sector constantly growing involves developing new researches aiming to determine the benefits of using different feeding strategies, and how these strategies influence economic and productive parameters (Gutiérrez et al., 2015; Janssen et al., 2017). Tilapia are organisms with protein requirements from inferior food chains and feeding habits that tend to be herbivorous (Montoya-Camacho et al., 2018), nevertheless, intensive rearing models of tilapia in close systems require protein/ energy levels between 18 and 23 kg/MJ for maintaining an optimum growth at first stages, according to Kabir et al. (2018). Nitrogen-balance studies of reared tilapia in tanks suggested that the productivity of the food web is increased when reducing the P/E ratio in the diet below the optimum levels reported in literature. This situation has given rise to the study of the effect of P/E proportion in balanced feeds with high and low lipid levels on growth as well as on the use of nutrients. In that regard, research works realized by El-Sayed & Teshima (1992), Swelium et al. (2005) and Kaushik et al. (1995) where the published data indicated that the nitrogen maximum gain is 12 g/kg/ day, corresponding to a level of maintenance protein of 2 g/kg/day with a DP/DE ratio of 18 mg/kJ. Based on these background data, the specific objective of this study was to determine the effect of different dietary P/E levels on protein sparing for Oreochromis niloticus juveniles growth in controlled conditions.
In aquaculture, values of production economical profitability are available only for a few species of commercial interest, mainly for marine species. Econometric equations used for obtaining profitability studies in Nile tilapia are founded on indicators that do not contemplate the analysis of elevated levels in the discount rate and their effects on the net present value (NPV) by means of probabilistic models of sensitivity. For this, the second objective of this research focused on performing a profitability analysis of Nile tilapia rearing using different feeding strategies and different scenarios of evaluation of the cost/benefit ratio and the NPV. Integrating analytic criteria proposed by Janseen et al. (2017) to the model in the biological variables and criteria developed by Perea-Román et al. (2018) and also those developed by Phiri & Yuan (2018) in the indexes of economical profitability and in the sensibility coefficients determined in this modeling with tilapia.
The development of new policies in worldwide aquaculture has clear objectives for the economic development, employment and protection of the environment by applying new models of production focused on species of high commercial demand and low production costs. Tilapia is the second most cultivated fish worldwide, therefore, in order to increase production, innovative methods are required for integrating the rearing and minimizing the pollution caused by fish metabolism (Watanabe et al., 2002). Economic analyses coupled to productive models with environmental implications are used for identifying better strategies of productive handling that are technical, economic, and ecologically efficient in production systems in which issues like fixed price and the size of harvests have to be solved (Kaliba et al., 2006; Poot-Lopez et al., 2014). The production systems of Nilotic tilapia in greenhouse conditions have been addressed through economic modeling in the following researches: By Lutz & Kenneth (1998) for a production system in 4 monthsperiods with offsprings with a initial weight of 4.5 g; by Nasr-Allah et al. (2014) for the production of fingerlings; and by Poot-Lopez et al. (2014) in an analysis of ration size with regards to harvest size with inanition and satiety periods. However, this is the first study of our knowledge in which a model of production in greenhouse is being integrated for the production of only juvenile fish with an average harvest weight of 150 g, using different feeding strategies, which were validated in the research work with Nile tilapia performed by Bolivar et al. (2006), using as feeding model a regimen of alternating days versus a daily model, as well as in the work of Adewolu & Adoti (2010) who validated different feeding schemes with high, medium, and low levels of mixed protein on the growth and food utilization in African sharptooth catfish (Clarias gariepinus). The general objective of this research was to determine the profitability of Nile tilapia juveniles rearing in greenhouse by utilizing different production scenarios in the modeling.
Material and Methods
The graphic summary of the evaluation model used for defining the profitability analysis in the intensive production of tilapia juveniles is described in Figure 1.
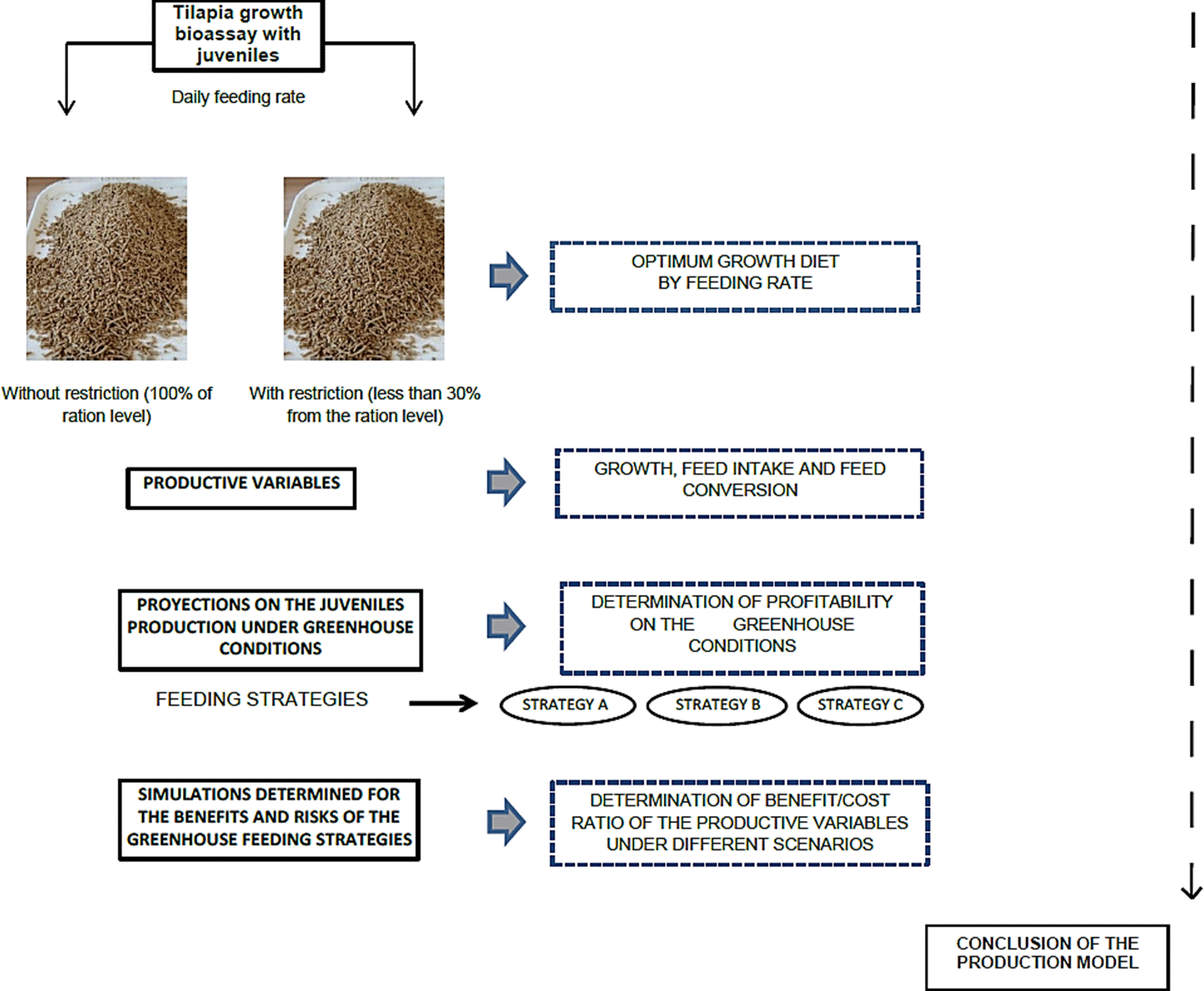
Figure 1 Conceptual model used to define the profitability analysis the intensive production of juvenile tilapia under greenhouse conditions (photograph from the feed pilot-plant of Academic Unit of Veterinary Medicine and Zootechnics, Autonomous University of Nayarit).
Development of diets and experimental organisms
The raw material used in this study was a batch of macro-ingredients that was formed by fish meals, soybean pasta meals, wheat meal and by dry moringa leaves pulverized in a Wiley mill model 4. For its proximal analysis the macro ingredients were sieved at 0.5 mm. In addition, as an energy source, fish oil and safflower oil were used, and as a supplement a commercial vitamin and mineral premixes. For the growth bioassay, four diets were formulated with P/E ratios of 18, 19, 20 and 21 kg/MJ by means of the software Nutrion-Pro, using lipid content as a main variation factor and maintaining a fixed protein level of 40 % (Table 1) based on the requirements for O. niloticus described by Diogenes et al. (2016). Diets were manufactured with the method described by Gutierrez et al. (2015), for which the resulting mass of the mixture of ingredients with 30 % water (weight/volume) was passed twice through a meat mill of 0.75 HP Harbor Beef Model G12 that had a two-millimeter die coupled at the end of the screw, later, the feed was dried in a stove with air flow for 24 h at 40 °C, once dried, the diets were sieved in order to remove fine particles and uniform pellets were stored at 18 °C until their use. A batch of commercial hormoned Nile tilapia fingerlings was obtained from the company Agro-Acuícola El Ventarron SPR de RL from Tlajomulco de Zúñiga, Jalisco, Mexico, which were acclimated in 12 m3-tanks for 30 days under experimental conditions of water quality and fed with a commercial diet of initiation from NutriPec brand with 40 % protein and 12 % lipids (Agribrands-Purina, Mexico) until achieving the adequate experimental weight.
Table 1 Chemical and energetic composition of the experimental diets used in the growth trial with juvenile Nile tilapia.
| Ingredients on wet basis (g/kg) | Experimental diets | |||
| D8 | D12 | D16 | D20 | |
| Wheat flour1 | 316.7 | 265.9 | 241.1 | 200.0 |
| Sardine fishmeal2 | 225.0 | 225.0 | 225.0 | 225.0 |
| Squid meal2 | 145.2 | 155.1 | 160.0 | 168.0 |
| Extracted soybean meal1 | 130.0 | 130.0 | 130.0 | 130.0 |
| Corn starch flour3 | 50.0 | 50.0 | 29.2 | 21.5 |
| Moringa leaves flour4 | 50.0 | 50.0 | 50.0 | 50.0 |
| Salmon oil2 | 30.0 | 50.0 | 70.0 | 90.0 |
| Carrageenan5 (binder) | 20.0 | 20.0 | 20.0 | 20.0 |
| Premix of vitamins and minerals6 | 20.0 | 20.0 | 20.0 | 20.0 |
| Safflower oil7 | 13.0 | 33.9 | 54.6 | 75.4 |
| Tocopherol 400 UI8 (lipid preserver) | 0.10 | 0.10 | 0.10 | 0.10 |
| Total sum of ingredients (g) | 1000 | 1000 | 1000 | 1000 |
| Chemical composition and energy content (dry basis; mean+± ED). | ||||
| Crude protein (g/kg)9 | 400.2±8.1 | 401.9±0.1 | 402.3±2.2 | 399.9±1.8 |
| Dry matter (g/kg)10 | 938.5±1.8 | 943.6±0.7 | 984.4±0.3 | 983.2±0.1 |
| Crude fiber (g/kg)* | 27.5 | 27.5 | 27.5 | 27.6 |
| Ash (g/kg)11 | 60.5±2.1 | 67.9±0.1 | 68.6±0.4 | 79.8±17.5 |
| Nitrogen-free extract (g/kg) | 359.3 | 319.7 | 313.6 | 260.8 |
| Ethereal extract (g/kg)12 | 91.1±2.3 | 126.7±2.1 | 172.4±4.6 | 215.1±0.5 |
| Gross energy MJ/kg13 | 19.29±0.08 | 20.25±0.02 | 21.14±0.08 | 22.16±0.02 |
| Protein/energy ratio (kg/MJ) | 21 | 20 | 19 | 18 |
*Theoretical value of Nutrion formulations.
Suppliers of Mexico and equipment used in laboratory analysis:
1Semillas Socorrito Tepic, Nayarit, México.
2Proteínas Marinas y Agropecuarias S.A. de C.V. Guadalajara, Jalisco, México.
3Maizena UNILEVER México, Tultitlán, Estado de México, México.
4Academic Unit of Veterinary Medicine and Zootechnics, Compostela, Nayarit, México.
5DGari Procesa Alimentos S.A. de C.V. Querétaro, México.
6VITAFORTE-A® PARFARM, S.A. México, D.F.
7Aceites Grasas y Derivados S.A. de C.V. Zapopan, Jalisco, México.
8Bayer de México S.A. de C.V.
9Gerhardt-DUMATHERM DT N40 analyzer (Gerhardt GmbH Co. Konigswinter, Germany).
10TerLab Mod. MA12D stove (TerLab S.A. de C.V., Jalisco, México).
11"NOVATE CH Mod. EI35-EA muffle (DICLAB A.C. Tlaquepaque, Jalisco, México).
12 Fat extraction equipment LABCONCO (LABCONCO Co. Kansas City, MO, USA).
13IKA C6000 isoperibolic calorimeter (IKA Inc. Wilmington, NC, USA).
Proximal and energy analyses of the diets
Samples of meals as ingredients, and diets were finely ground and analyzed in its proximal chemical composition of raw protein (Nitrogen x 6.25), ethereal extract (lipids), moisture, ash and crude fiber with standardized methods by AOAC (2006) in the laboratory of bromatological analyses of the Academic Unit of Veterinary Medicine and Zootechnics of the Autonomous University of Nayarit. Next, raw energy content was determined by means of an isopeliboric calorimeter. Nitrogen-free extract was calculated from the proximal composition as % NFE = 100 - (% protein + % ethereal extract + % ash + % moisture + % crude fiber).
Growth bioassay
The experimental system consisted in 24 tanks of 1200-L connected to a closed water recirculation system coupled to a bio-filter previously conditioned with nitrogen-fixing bacteria BioPro® Nitrobacter (Hobby Pet, Monterrey, Nuevo León, México) for treating the residual water from the tanks with a water renewal rate of approximately 360 % for 24 h. In the bioassay, juveniles (initial weight 9.6 ± 0.2 g) were assessed during 45 days in controlled conditions of temperature (27 ± 2 °C), dissolved oxygen (>6 mg/L) and photoperiod (12 h light: 12 h darkness), at a rearing density of 10 tilapia/tank. Three diets were supplied in a design with apparent satiety feeding (control diets), and three diets with a feeding strategy with a restriction of 30 % compared to the consumption of the control treatment in an experimental design randomized in triplicate. During the bioassay, biometrics were performed on days 0, 15, 30, and 45 after a 24 h period without feeding in order to standardize the weight of the animals. Water quality parameters as dissolved oxygen and temperature were measured once a day at 8.00 am using an oximeter model AZ8403. Ammonium, nitrites and nitrates contents were determined ever three days by means of a commercial colorimetric kit API-SALTWATER for freshwater, and pH was measured with a manual potentiometer. The rearing system was installed in the Academic Unit of Veterinary Medicine and Zootechnics of the Autonomous University of Nayarit, tilapia were conditioned in a tank of 2 m3 capacity at a temperature of 27 ± 0.5 °C and dissolved oxygen of 5.0 ± 0.7 mg/mL under clear water conditions.
Productive parameters and economic analysis of the bioassay
At the end of the bioassay, productive zootechnical parameters were determined with standard formulas for fish and using criteria determined by Jauralde et al. (2011) to define the thermal growth coefficient by using the formula
The parameters of economic gains by effect of each experimental diet were determined by using the following equations used by Lozano et al. (2007): 1) Economic conversion ratio (USD $/kg of tilapia); ECR = feed conversion (kg of diet/kg of tilapia) x feed cost (USD $/kg of diet). 2) Economic profit index (USD $/ tilapia); EPI = [final weight (kg/tilapia) x tilapia sale price (USD $/kg)] - [ECR (USD $/kg of tilapia) x weight increase (kg)].
Profitability analysis
With the purpose of analyzing the profitability in terms of costs reduction of an intensive productive system of tilapia juveniles in greenhouse conditions, criteria described by Perea-Román et al. (2018) and Phiri & Yuan (2018) were utilized in order to establish the benefit/cost ratio (B/C) of three feeding strategies with feeds of different protein compositions when using the productive parameters of O. niloticus as theoretical basis, which were determined by means of the experimental bioassay with a diets with different protein/energy ratios. This process was designated as a baseline analysis and was realized by using the results of the growth bioassay with regards to the optimum growth rate of O. niloticus for the productive conditions from Compostela, Nayarit, Mexico.
Sensibility analysis
In order to determine the effect of the average annual total cost defined in the productive system with the higher profitability (baseline), a sensibility analysis was applied to the marginal incomes, assuming the following scenarios of production with accumulated increases in both analyzed variables: (Case 1) 10 % increase in feeding and 5 % in sale price of the product; (Case 2) 20 % increase in feeding and 5 % in sale price of the product; (Case 3) 30 % increase in feeding and 5 % in sale price of the product; (Case 4) 10 % increase in feeding and 10 % in sale price of the product; (Case 5) 20 % increase in feeding and 10 % in sale price of the product; (Case 6) 30 % increase in feeding and 10 % in sale price of the product. Additionally, B/C ratio of each scenario of production was determined to establish conclusions about the final profitability of this study in a five-years period.
Statistical analysis
The productive and economic parameters of the growth bioassay were analyzed for their normality and homogeneity of variances with Shapiro-Wilk’s and Barttley’s tests, respectively (Sokal & Rohlf, 1995). A one-way ANOVA was performed on the determined variables and a Tukey’s multiple comparison test in order to separate differences among groups with a significance level α = 0.05. The calculations were processed with the STATISTICA kit Version 6.0 (StatSoft, Inc. Tulsa OK, USA). An analysis with 5000 repetitions was applied for the net present value (NPV) in a five-years financial run, with α = 0.01, applying a variation of ± 1 % in the standard deviation of the studied variables, by means of a risk simulator software @RISK 7.5 (Palisade Corporation, Ithaca, NY, USA), from which the average profits were obtained considering three discount rates of the project (5 %, 10 % and 15 %).
Results and Discussion
Water quality and diet composition
Parameters of water quality, such as ammonium, nitrites, and nitrates presented values of 0.12 ± 0.22 mg/L, 2.48 ± 1.78 mg/L and 86.67 ± 36.67 mg/L respectively, which indicated a high variability in water nutrients throughout the experiment with presence of null or very low values due to the conversion process of the nitrogenized residues in the form of ammonia by nitrifying bacteria present in the biological filter, related to this, a survival rate of 100 % was recorded in all of the treatments. These values were found within the range of standards reported in literature as adequate for the tilapia rearing (Ridha & Cruz, 2001). The composition of ingredients of the experimental growth diets are presented in Table 1, which had a P/E ratio from 18 to 21 kg/MJ, which was due to the inclusion of 8 %, 12 %, 16 % and 20 % of lipids, in other words, feeds were isoproteic (400 g/kg) but not isoenergetic in order to evaluate the hypothesis of the energy on the growth in a design with or without feed restriction.
Effect of the diet on productive variables of O. niloticus
Zootechnical parameters of growth and feed use were shown in Table 2. Feed energy content was considered as the major criterion to control fish feed intake (Lupastch et al., 2001). In this study the level of the P/E ratio of the feed did not have affect the growth of O. niloticus among the different treatments (p>0.05) under the evaluated conditions, which is probably because the diets covered the requirement of maintenance and growth regardless of the dietary condition. Results indicated that the lower food intake was present with D8R diet (feeding protocol with 30 % restriction), consequently the consumed protein allowed for optimizing parameters of feed conversion and protein efficiency (p<0.05), hence this treatment was considered as the optimum to be evaluated in the next stage by means of a profitability analysis in tilapia juveniles rearing in response to the biological indicators recorded for growth rate, thermal growth coefficient, total feed and protein intake and feed efficiency. Likewise, results obtained for zootechnical parameters in this treatment were reflected in significant increases of economic conversion indexes of the feed and there was no negative effect in economic profitability indexes in the different treatments (p<0.05).
Table 2 Zootechnical and economic parameters of the growth trial determined for 45 days in juvenile Nile tilapia in two feeding conditions (mean ± ED, n=3).
| Apparent satiety feeding (diets D8-D20) | Feeding with 30% of restriction (diets D8R-D20R) | |||||||
|---|---|---|---|---|---|---|---|---|
| D8 | D12 | D16 | D20 | D8R | D12R | D16R | D20R | |
| Live final weight (g) | 150.4 ± 3.36a | 145.96 ± 12.70a | 146.6 ± 5.03a | 137.70 ± 10.69a | 134.78 ± 4.14a | 137.53 ± 4.50a | 133.75 ± 5.96a | 139.15 ± 12.60a |
| Growth rate (%/day) | 6.25 ± 0.05a | 6.18 ± 0.18a | 6.20 ± 0.07a | 6.07 ± 0.17a | 6.04 ± 0.05a | 6.07 ± 0.08a | 6.01 ± 0.08a | 6.10 ± 0.20a |
| Thermal growth coefficient x 1000 | 12.15 ± 0.03a | 11.62 ± 0.65a | 11.68 ± 0.48a | 11.30 ± 0.69a | 11.33 ± 0.62a | 11.25 ± 0.17a | 11.07 ± 0.77a | 11.12 ± 0.59a |
| Accumulated thermal degrees (°C) | 272 ± 14a | 280 ± 10a | 279 ± 7a | 280 ± 11a | 277 ± 10a | 281 ± 8a | 282 ± 13a | 286 ± 9a |
| Feed intake (g/tilapia/day) | 5.38 ± 0.14b | 5.74 ± 0.22a | 5.84 ± 0.13a | 5.69 ± 0.07a | 3.61 ± 0.02d | 3.84 ± 0.02cd | 3.98 ± 0.01c | 3.79 ± 0.07cd |
| Protein intake (g/tilapia/day) | 2.15 ± 0.06b | 2.31 ± 0.09a | 2.35 ± 0.05a | 2.28 ± 0.03a | 1.44 ± 0.01d | 1.54 ± 0.01cd | 1.60 ± 0.004c | 1.52 ± 0.03cd |
| Protein efficiency ratio (g/g) | 1.55 ± 0.07a | 1.40 ± 0.07a | 1.39 ± 0.07a | 1.35 ± 0.11a | 2.09 ± 0.05b | 1.98 ± 0.07b | 1.86 ± 0.08b | 2.05 ± 0.21b |
| Feed conversión (kg/kg) | 1.61 ± 0.07a | 1.78 ± 0.08a | 1.80 ± 0.09a | 1.86 ± 0.15a | 1.19 ± 0.03b | 1.25 ± 0.05b | 1.34 ± 0.06b | 1.23 ± 0.13b |
| Economic conversión ratio1 (USD $/kg of tilapia) | 3.62 ± 0.17bc | 4.25 ± 0.20ab | 4.39 ± 0.23a | 4.83 ± 0.38a | 2.68 ± 0.07d | 3.00 ± 0.11cd | 3.27 ± 0.14cd | 3.18 ± 0.34cd |
| Economic profit index2 (USD $/tilapia) | 3.03 ± 0.09a | 2.85 ± 0.26a | 2.84 ± 0.12a | 2.63 ± 0.17a | 2.89 ± 0.07a | 2.89 ± 0.11a | 2.78 ± 0.12a | 2.90 ± 0.30a |
Different letters in the superscripts of each row indicate significant differences when comparing both conditions independently (Tukey, p<0.05). 1Considering in the calculation the feed prices of $ 2.24, $ 2.39, $ 2.44 and $ 2.59 for diets D8, D12, D16 and D20 respectively, values expressed in US dollars with prices of the raw material of November 2018. 2Tilapia sale price was calculated at 2.24 USD $/kg (≈ 6.5 fishes/kg).
In the literature it was reported that optimal levels of the digestible protein and digestible energy (DP/DE), determined according to the size of the tilapia, present a high variability (Haidar et al., 2018). These researches comprise a wide range of DP/DE with levels of 16.7 to 27 g/MJ, demonstrating that decreasing DP/DE values increases the efficiency of protein utilization at levels up to 53 %. One of the factors that probably affect this ratio is the use of lipids, which tends to decrease with regards to the increase of protein and fish size. In this research, the growth of the fish with respect to the P/E ratio in the diet did not show significant differences among the different diets with and without feed restriction, evidencing that there was no positive effect in proteinsparing mechanism for growth with regards to the increase of feed energy level. The phenomenon of protein sparing has been extensively studied during the last three years in different species of freshwater and marine fish (Jian et al., 2016; Wu et al., 2016; Cheng et al., 2017; Francis & Turchini, 2017; Rasool et al., 2018; Weihe et al., 2018). This process indicates that during growth stage, fish manifest protein sparing for the formation of muscular accretion by preferably using lipids and carbohydrates as sources of energy, as demonstrated in the researches of Azevedo et al. (2002) in diets for the Atlantic salmon (Salmo salar) with different levels of DP/DE (20, 18 and 20 g/MJ) supplied in two feeding levels (100 % or 85 % of the requirements) and also as documented in research performed by Jantrarotai et al. (1998) realized on hybrid freshwater catfish (Clarias macrocephalus x C. gariepinus) fingerlings which were fed with diets having different protein levels (20 %, 30 % and 40 %) and energy (275, 300 and 325 kcal of digestible energy/100 g). In this study, unlike previous works, diets were not used in a design with different protein levels, since it was required to design a model of growth where the maximum growth rate would be found according to nutritional and energetic quality of the diet, and that this process would allow for the maximum value of the thermal growth coefficient (TGC), suggesting that this type of design affected in the non-detection of the phenomenon of protein sparing in reference to the results found in the works mentioned. The average TGC determined in this study was 11.44 and is comparable to that reported for Salmo salar (12.6 ± 0.08) by Janssen et al. (2017); however, this value is far more superior than the one reported for gilthead bream (Sparus aurata) by Jauralde et al. (2011) who registered accumulated thermal units (ATUs) in ranges of 704‒41079 and values of TGC of 0.066‒1.58 for different experiments in an experimental period between 64 and 90 days, and in turn with conversion rates from 1.3 to 2.75. What is valued from these comparisons is that there is a direct relation between TGC and feeding rate, an aspect defined by Janssen et al. (2017) as “thermal feed intake coefficient” which is directly dependent of TGC, whereby the validity of the proposed growth model is centered on feed rate utilization for O. niloticus depending on ATUs in a 45 days-period, and later the application of this principle in the proposed design in the annual model and during the evaluated five yearsperiod (Tables 2, 3 and 4), respectively.
Table 3 Profitability analysis of tilapia production with average weight of 150 g in an annual cycle under intensive conditions in tanks with different feeding strategies.
| Strategy A | Strategy B | Strategy C | ||||
|---|---|---|---|---|---|---|
| 1H:1Lx | 2H:1Ly | 3H:2Lz | ||||
| Productive parameters under greenhouse conditions with 14 tanks of 12 m3 | ||||||
| Total volume of the system (m3/tank/year)1 | 432 | 432 | 432 | |||
| Initial culture density (tilapia/m3/tank)2 | 218 | 218 | 218 | |||
| Initial biomass of fingerlings (kg/period/year) 2 | 42 | 42 | 42 | |||
| Accumulated thermal units (0C/period/year)3,4 | 310.6 | 310.6 | 310.6 | |||
| Accumulated thermal units (°C/year) 3,4 | 1,800 | 1,800 | 1,800 | |||
| Periods of culture (period/year)5 | 6 | 6 | 6 | |||
| Periods time culture (days/period/year) 5 | 53.5 | 53.5 | 53.5 | |||
| High value consumed protein (kg/period/year)6 | 1622 | 3245 | 3245 | |||
| Low value consumed protein (kg/period/year)7 | 1014 | 676 | 507 | |||
| Protein intake (g/tilapia/day) | 1.17 | 1.74 | 1.67 | |||
| Feed conversion (period/year) 5 | 1.2 | 1.1 | 1.0 | |||
| Biomass tank performance (kg/period/year)8 | 5,660 | 6,226 | 7,358 | |||
| Total biomass yield (kg/year) 8 | 33,285 | 36,614 | 43,271 | |||
| Variable costs ($ thousands of dollars USD)* | ||||||
| O. niloticus fingerlings ($/year) | $ | 6.28 | $ | 6.28 | $ | 6.28 |
| High protein feed ($/year) 6 | $ | 26.70 | $ | 35.60 | $ | 40.05 |
| Low protein feed ($/year) 7 | $ | 19.42 | $ | 12.95 | $ | 8.21 |
| Medicines ($/year) | $ | 0.10 | $ | 0.10 | $ | 0.10 |
| Electricity ($/year) | $ | 2.82 | $ | 2.92 | $ | 3.01 |
| Workforce $/year) | $ | 2.00 | $ | 2.00 | $ | 2.00 |
| Well water supply ($/year) | $ | 0.78 | $ | 0.78 | $ | 0.78 |
| Installed geomembranes of 16 m3 ($/year) | $ | 14.57 | $ | 14.57 | $ | 14.57 |
| Electrical and equipment installations ($/year) | $ | 2.73 | $ | 2.73 | $ | 2.73 |
| Equipment maintenance ($/year) | $ | 0.99 | $ | 0.99 | $ | 0.99 |
| Fixed costs ($ thousands of dollars USD) * | ||||||
| Equipment ($/year) | $ | 17.38 | $ | 17.38 | $ | 17.38 |
| Land rent ($/year) | $ | 0.12 | $ | 0.12 | $ | 0.12 |
| Administrative expenses and marketing ($/year) | $ | 0.72 | $ | 0.72 | $ | 0.72 |
| Economic analysis of annual profitability ($ thousands of dollars USD) * | ||||||
| Total costs (TC) | $ | 94.61 | $ | 97.14 | $ | 96.95 |
| Fixed costs (FC) | $ | 76.39 | $ | 78.92 | $ | 78.73 |
| Total variable costs (TVC) | $ | 18.21 | $ | 18.21 | $ | 18.21 |
| Average variable costs (AVC) | $ | 0.55 | $ | 0.50 | $ | 0.42 |
| Yield per year in thousands of kg (Q) 8 | 33.29 | 36.61 | 43.27 | |||
| Sale price in dollars per kg of tilapia (P) | $ | 2.49 | $ | 2.49 | $ | 2.49 |
| Gross income (R) | $ | 83.01 | $ | 91.31 | $ | 107.91 |
| Total gain (TG) | $ | 64.79 | $ | 73.09 | $ | 89.69 |
| Marginal gain (MG) | $ | 0.03 | $ | 0.04 | $ | 0.05 |
| Benefic/cost ratio (BCR) | 0.88 | 0.94 | 1.11 | |||
| Balance price in dollars (BP) | $ | 2.84 | $ | 2.64 | $ | 2.24 |
| Production of equilibrium in thousands of kg (PE) | 39.25 | 39.53 | 37.99 | |||
| Gross profit per kg of tilapia in dollars (GPK) | $ | 1.95 | $ | 2.00 | $ | 2.07 |
xStrategy A: Feeding (1:1) 24 h with high protein and 24 h with low protein as accumulated time.
yStrategy B: Feeding (2:1) 48 h with high protein and 24 h with low protein as accumulated time.
zStrategy C: Feeding (3:2) 36 h with high protein and 48 h with low protein as accumulated time.
1Production system modeled in 12 tanks of 36 m3 with top cover of reinforced plastic.
2Modeling with 291 tilapias/m3 with an initial weight of 1 g and a price of $ 0.02 USD by fingerling.
3Considering a thermal growth coefficient of 11.33 from Table 2.
4Statistical variation from Compostela, Nayarit (28.9‒24.7 ºC) for a time series of 10 years.
5Calculations with growth rate of the O. niloticus and the protein consumption rate of Table 2.
6Calculated with a commercial feed price of $ 1.003 USD/kg with 35 % of protein.
7Calculated with a commercial feed price of $ 1.253 USD/kg with 25 % of protein.
8Estimated value with a total cumulative mortality in the culture of 2 %.
Equations: R = P x Q; TC = TVC + FC; AVC = TVC/Q; TG = Q x (P ‒ AVC) ‒ FC; MG = TG/TC; BCR = R/TC; PE = AVC + (FC/Q); PE = FC/ (P ‒ TVC/Q) according to the Phiri and Yuan approaches described in 2018. The criterion of GP was determined with the equation GP = TG/Q as reported by Besson et al. (2016).
*The conversion of dollar to Mexican peso used was: 1 USD $ = 20.05 pesos (November, 2018).
Table 4 Simulation of benefits and risks in different tilapia production scenarios regarding changes in the mean values of the feed cost and in the fish sale price over a period of 5 years based on the projections determined in Table 3.
| Limiting factors in the calculations: initial weight of 10 g, final weight of harvest of 150 g and an average annual production of 43,271 kg | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameters or simulations | BPC | GPT | TGI | CFM | TFC | TVC | BCR | NPV (5%) | NPV (10%) | NPV (15%) |
| Baseline performance | $2.13 | $0.94 | $539.54 | $241.33 | $393.67 | $21.55 | 1.3 | $ 85.27 ± 4.10 | $ 71.71 ± 3.38 | $ 60.83 ± 2.81 |
| Feed cost >10% (A)* | $2.23 | $0.84 | $539.54 | $260.64 | $412.98 | $21.55 | 1.2 | $ 68.97 ± 4.21 | $ 57.80 ± 3.47 | $ 48.85 ± 2.89 |
| Feed cost >20% (B) * | $2.33 | $0.74 | $539.54 | $279.95 | $432.28 | $21.55 | 1.2 | $ 52.67 ± 4.29 | $ 43.89 ± 3.54 | $ 36.86 ± 2.94 |
| Feed cost >30% (C) * | $2.43 | $0.64 | $539.54 | $299.25 | $451.59 | $21.55 | 1.1 | $ 36.37 ± 4.13 | $ 71.71 ± 3.40 | $ 60.83 ± 2.83 |
| Fish sale price <5% (D) * | $2.13 | $0.78 | $512.56 | $208.48 | $393.67 | $21.55 | 1.2 | $ 85.27 ± 82.8 | $ 1,437.7 ± 68.2 | $ 1,219.6 ± 56.8 |
| Fish sale price <10% (E) * | $2.13 | $0.62 | $485.59 | $208.48 | $393.67 | $21.55 | 1.2 | $ 85.27 ± 4.14 | $ 71.71 ± 3.41 | $ 60.83 ± 2.84 |
| Fish sale price <15% (F) * | $2.13 | $0.46 | $458.61 | $208.48 | $393.67 | $21.55 | 1.1 | $ 85.27 ± 4.09 | $ 71.71 ± 3.37 | $ 60.83 ± 2.80 |
| Fish sale price >5% (G) * | $2.13 | $1.10 | $566.51 | $208.48 | $393.67 | $21.55 | 1.4 | $ 98.35 ± 4.18 | $ 82.35 ± 3.45 | $ 69.53 ± 2.87 |
| Fish sale price >10% (H) * | $2.13 | $1.26 | $593.49 | $208.48 | $393.67 | $21.55 | 1.4 | $ 111.44 ± 4.41 | $ 92.99 ± 3.63 | $ 78.23 ± 3.02 |
| Simulation-1 A + G* | $2.23 | $1.00 | $566.51 | $260.64 | $412.98 | $21.55 | 1.3 | $ 100.27 ± 4.48 | $ 83.99 ± 3.69 | $ 70.94 ± 3.07 |
| Simulation-2 B + G* | $2.33 | $0.90 | $566.51 | $279.95 | $432.28 | $21.55 | 1.3 | $ 65.76 ± 4.47 | $ 54.53 ± 3.69 | $ 45.57 ± 3.07 |
| Simulation-3 C + G* | $2.43 | $0.80 | $566.51 | $299.25 | $451.59 | $21.55 | 1.2 | $ 65.76 ± 4.36 | $ 54.53 ± 3.60 | $ 45.57 ± 2.99 |
| Simulation-4 A + H* | $2.23 | $1.16 | $593.49 | $260.64 | $412.98 | $21.55 | 1.4 | $ 95.14 ± 4.40 | $ 79.08 ± 3.63 | $ 66.25 ± 3.02 |
| Simulation-5 B + H* | $2.33 | $1.06 | $593.49 | $279.95 | $432.28 | $21.55 | 1.3 | $ 78.84 ± 4.54 | $ 65.18 ± 3.74 | $ 54.27 ± 3.11 |
| Simulation-6 C + H* | $2.43 | $0.96 | $593.49 | $299.25 | $451.59 | $21.55 | 1.3 | $ 62.54 ± 4.62 | $ 51.27 ± 3.81 | $ 42.29 ± 3.17 |
*Calculations made on the data of the optimal conditions determined in the performance of the baseline (+ or ‒). Values expressed in thousands of USD dollars except the B/C ratio. Nomenclature: BPC = biomass production cost per ton; GPT = Gross profit per ton of tilapia; TGI = total gross income; CFM = average cost of the proposed feeding model (3H:2L); TFC = total fixed costs; TVC = total variable costs; BCR = benefic/cost ratio; NPV = net present value. The conversion of dollar to Mexican peso used was: $ 1 USD = 20.05 pesos (November, 2018).
Growth models by means of logarithmic equations depending on optimum growth temperature have been evaluated in tilapia by Baras et al. (2002), also by means of equations of daily growth with standardized exponents according to Trong et al. (2013), and more recently by Omasaki et al. (2017) with TGC records of 1.30 in tilapia during the growth phase of 5 g to 250 g in farms from Kenia at a density of 3 fish/m2. Nevertheless, too few data are currently available on these elements, in conditions of intensive rearing for the region of Latin America, being necessary going deeper into these determinations. Some researchers have determined that the importance of TGC in the biological model lies on its simplicity since it is a limiting condition that affects production (Janssen et al., 2017).
The compensatory growth is defined as an unusually fast growth stage in which animals are subjected to a partial or total nutritional restriction, and the exploitation of this phenomenon can result in benefits on growth rate and feeding efficiency (Gabriel et al., 2018). In fish like barramundi (Lates calcarifer) there are evidences for compensatory growth when they were fed at 0 %, 25 %, 50 % and 75 % of the apparent satiety level during two weeks before a period of five weeks with feeding by satiety in which there were negative significant statistical differences in the quantity of consumed food with regards to the control treatment (Tian & Quin, 2003). This phenomenon has been demonstrated in rainbow trout (Salmo gairdneri) (Dobson & Holmes, 1984), in channel catfish (Ictalurus punctatus) (Gaylord & Gatlin, 2001) and in European bass (Dicentrarchus labrax) (Adakli & Tasbozan, 2015), among others. The compensatory growth of tilapia has been evidenced in the works of Wang et al. (2000) in Oreochromis mossambicus x O. niloticus hybrids with an initial weight of 4.34 ± 0.03 g in an experiment with a duration of 8 weeks, evidencing that one fasting week allowed for growth rate similar to those observed in the control. A similar response was also found in fish with an initial weight of 8.9 ± 0.2 g fasten for one week and for a 12-week refeeding period (Abdel-Tawwab et al., 2006). More recently, the investigation of Liu et al. (2018) evaluated a feeding system with a low-protein diet (25 %) supplied for 10 days in comparison with a high-protein diet (35 %) for 20 days with O. niloticus with an initial weight of 11.02 ± 0.05 g and found similar results to that of the control. Works on other species of tilapia juveniles like O. mossambicus developed by Gabriel et al. (2017; 2018) suggested that hyperphagia could be the main contributor to the high growth rates during the compensatory period, and in fasting periods, results suggested that fish adjust their metabolic rate. In summary, it is known from these investigations that the compensatory growth rate of tilapia can be maintained in a manner similar to fish fed at satiety when a constant feeding rate is used with intervals providing diets with high-level and low-level of protein
Profitability analysis
The study of the baseline represented on Table 2 was defined as the starting point from the biologic model to the economic model, in which it was determined that feed economic conversion increased in diets with feeding to apparent satiety and finding the best results in terms of feed use in D8R diet since it presented the lowest value (p<0.05).
Profitability analyses by means of simulation models in aquatic organisms have been taken into account in the decision-making process for organisms like: the Peruvian scallop (Argopecten purpuratus) in order to define the fattening model based on the harvest size (Molina et al., 2012); the lambari tetra mojarra (Hyphessobrycon balbus) in order to analyze the economic viability of the investment by means of the internal rate of return of the project with an five-years economic viability analysis (Sabbag et al., 2011); the Atlantic salmon (Salmo salar) for its rearing in marine ranches with other species like Arctic char (Salvelinus alpinus) and European lobster (Homarus gammarus) and examining both biological and economic bases, by using the NPV approach on the annual operation costs (Moksness et al., 1998); the threadfin (Polydactylus sexfilis) in order to evaluate the feasibility of its production in cages by means of a sensibility analysis with an increase of production density, survival rate and growth rate (Kam et al., 2003), to mention a few examples. In O. niloticus, the research performed by Ponzoni et al. (2007) stands out, in which an economic modeling of annual gains of low and high genetic traits of inheritability of tilapia was applied on parameters of harvest weight, survival, and consumed food, with a discount rate from 5 % to 15 % to the model, finding positive benefits up to 75 % of the cost/benefit ratio with regards to the basal condition even at the superior level. The work realized by Perea-Román et al. (2018) stands out as well, in which the use of the chemical silage of viscera of trouts was economically evaluated at levels of 10 %, 20 % and 30 % in diets for red tilapia, emphasizing that when increasing the inclusion of silage, the cost of the food was significantly reduced up to a 22.97 %.
The sensitivity analysis showed that for each rearing scenario the effects on productivity were determined with regards to the reduction of the production costs (Table 4). Nonetheless, the most significant reduction of profitability was observed when the production scenarios sales price of 5-10 % and cost feeding cost of 10-30 % were combined, where the benefit/cost ratio fluctuated between 1.2 and 1.4, showing a trend to reduce profitability when the price of the feed increases to the highest estimated level (30 %) upon production costs. Profitability analysis by annual cycle (Table 3) indicated that there were variations in percentages of the obtained biomass, total marginal profit, benefit/cost ratio, production of equilibrium and gross profits in favor of feeding strategy C (3H:2L). This trend has been well documented in literature, regarding this; the revision realized by Ali et al. (2003) stands out, where a deep revision was done about why animals grow at rates below their physiological capacity. These elements are fundamental for the selection process of the studied variables in the growth bioassay and in the profitability evaluations of O. niloticus rearing, developed in the models from Tables 2, 3 and 4 respectively.
Traditional NPV analysis models are centered on the profitability of a determined business unit, while a benefit/cost analysis has a far wider reach. The benefit/ cost ratio is a common indicator that is used for the elaboration of budgets of capital to determine the profitability of a proposed investment, therefore, an investment if profitable if the benefit/cost ratio is greater than 1 (Phiri & Xuan, 2018). In this sense, results of the profitability analysis (Table 4) presented positive values, which allowed for establishing a production cost per ton of $ 2.13 thousand dollars, in addition to a gross profit per ton of biomass of $ 0.94 thousand dollars, establishing as determined in the baseline of the calculation with a price of $ 2.24 dollars/kg of produced tilapia. This profit margin is negative and positively modified in the projections of scenarios 1 to 6 (box in Table 4), despite this, theoretical profits were determined for the gross profit per ton between $ 0.80 and $ 1.16 thousand dollars, considering that there were increases of $ 2.23 to $ 2.43 thousand of dollars in production costs of the biomass. These results could be positive from a biological point of view based on benefit/cost ratio analysis, since increasing profits could be obtained between 20 % and 40 % for each invested dollar. To our knowledge, this is the first study focusing on determining benefit/cost ratio of the intensive production of tilapia juveniles in greenhouse from a biological point of view. However, a deeper analysis is required involving aspects like environmental costs, aggregated value, feeding strategies, types of bio-flocs and aquaponics systems as sustainable models.
Conclusions
Nile tilapia juveniles did not present a phenomenon of protein sparing for growth depending on protein/energy levels from 18 to 21 kg/MJ, however, a thermal growth coefficient of 11.33 allowed to establish an adequate projection of the daily weight gain of tilapia based on a feeding rate of 3.61 g/tilapia/day, without affecting economic profit index of the feed. The production of O. niloticus determined by the benefit/cost ratio of the project showed positive figures with an increase of 26 % in the economic return rate when using a threeday feeding strategy with high-protein diets and a two days-feeding with a low-protein diet with regards to the one-day alternate feeding strategy with the high-protein diet and one day with the low-protein diet. The different production scenarios calculated with the current net value and the benefit/cost ratio contributed with positive figures at the end of a five-year period, therefore, the utility of this model is feasible for the intensive production of juveniles up to an average weight of 150 g with 6 rearing cycles per year of production.











 texto en
texto en 



