Introduction
Continuous and extensive monitoring of vegetation is necessary for the understanding of essential ecosystem processes such as carbon storage that has implications for natural resource availability and climate regulation (George & Schillebeeckx, 2018; Mclaughlin et al., 2017). Understanding the aboveground biomass carbon (ABCS) storage is fundamental, not only because it represents about 30 % of the total carbon in terrestrial ecosystems, but also because the ability of communities to exchange and storage this element depends on this reservoir (Kumar & Mutanga, 2017). Tree species, possess the greatest capacity for carbon storage within communities, attributed to amount of biomass contained in their structures (Bradley et al., 2006; Montaño et al., 2016). Thus, studying aboveground carbon biomass (ABCS) in tree species is key to improving our understanding of the carbon storage process in ecosystems.
Several carbon storage studies have been conducted in ecosystems of temperate zones and tropics; however, research in arid and semi-arid areas is limited (Biederman et al., 2018; Briones et al., 2018; Issa et al., 2020; Montaño et al., 2016). This highlights a lack of crucial information, as arid and semi-arid areas cover a significant portion of the Earth's surface (>40 %) and influence interannual variation in the global carbon cycle, a dynamic affected by the continuous and extensive pressure of human activities (Ahlström et al., 2015; Biederman et al., 2018; Poulter et al., 2014). Given these factors, the absence of carbon-related studies in arid areas represent a significant knowledge gap that should be addressed, to achieve a responsible management of ecosystems and the conservation of their processes.
In recent years, the use of remote sensors (e.g., RGB, multispectral, and thermal) mounted on Unmanned Aerial Vehicles (UAVs) and photogrammetric techniques for vegetation monitoring have been incorporated (Iglhaut et al., 2019; Kim & Chung, 2021; Sun et al., 2021), increased the capacity to collect information at high spatial and temporal resolution. Studies using sensors mounted on UAVs have helpend in the vegetation classification, census, and characterization (Cornejo-Denman et al., 2018; Gallardo-Salazar & Pompa-García et al., 2020; Vivar-Vivar et al., 2021), and more recently, the estimation of aboveground biomass (Holiaka et al., 2021; Navarro et al., 2020). Among the advantages of the continuous use of UAVs in vegetation studies are the accessibility and availability of specialized equipment and software to carry out geospatial routines with high precision (Creasy et al., 2021; Holiaka et al., 2021; Kim & Chung, 2021; Navarro et al., 2020). This facilitates the continuous monitoring of areas of interest, which is challenging with techniques involving higher costs (Briones et al., 2018; Gallardo-Salazar & Pompa-García, 2020; Pordel et al., 2018). As a result, technologies including the use of UAVs for capturing aerial images are increasingly being utilized (Sun et al., 2021). However, to understand the value of these approaches, their systematic evaluation is necessary.
The objective of this study was to develop predictive models using high-resolution aerial images, for the estimation of ABCS in tree species of representative communities of subtropical scrub, in the central Sonora. Specifically, morphological metrics obtained with photogrammetric techniques and RGB images were used as explanatory variables in the ABCS models at the individual scale. Specifically, morphological metrics obtained using photogrammetric techniques and RGB images were used as explanatory variables in individual-scale ABCS models.
Materials and Methods
The aboveground carbon biomass of tree species was estimated using morphological metrics collected in the field (direct sampling) and allometric equations. Subsequently, vegetation metrics were obtained through aerial images (remote sampling), according to two methods: manual (digitization) and automatic (algorithm). Finally, using these metrics, predictive models of individual-level ABCS were generated.
Study Area
The study site is located at rancho El Churi, between latitudes 28° 40’ and 28° 45’ N, and meridians 110° 30’ and 110° 35’ W, municipality of La Colorada, Sonora (Figure 1). Climatic conditions are semi-arid according to the De Martonne aridity index (Acuña-Acosta et al., 2021). Average annual temperature is 22.8 °C, with maximums around 40 °C and minimums of 5 °C. Mean annual precipitation (476 mm) occurs in summer (July-September) and winter (December-February), with summer events contributing the majority (65 % to 85 %) of the total annual precipitation (Castellanos et al., 2022; Hinojo-Hinojo et al., 2019). The site shows high interannual variability in precipitation events, primarily influenced by the El Niño/Southern Oscillation (ENSO; interannual scale) and Pacific Decadal Oscillation (PDO; decadal scale) phenomena (Arriaga-Ramírez et al., 2010; Choza-Farías et al., 2021).
The dominant vegetation community is subtropical shrubland, and the land use is primarily for livestock grazing. As a result, the forage capacity of the native ecosystem has increased through selective clearing of tree species for the establishment of the exotic buffel grassland (Cenchrus ciliaris L). In the area, conspicuous stretches of modified subtropical shrubland converted into buffel grassland can be found (Hinojo-Hinojo et al., 2019).
Estimation of vegetation metrics in an open field
The census of individuals taller than 2 m was conducted during the summer (August, September, and October of 2019 and 2020), when vegetation is active and species identification is possible. The experimental design comprehended the selection of five sites in subtropical shrubland and five in buffel grassland, where 30 x 30 m quadrants (900 m2) were established, and trees taller than 2 m were measured. The following metrics were recorded for these individuals: a) maximum crown height using a clinometer (Suunto, Vantaa, Finland), b) two crown radii, measured orthogonally to each other with a measuring tape (r1 and r2), c) diameter at breast height (DBH), and d) location/coordinates of individuals using GPS (GPSMAP 62sc, Garmin Ltd, Kansas, United States). Height and radii metrics were used to estimate crown area (Ac = r1 * r2 * π) and crown volume (V = Ac * height) (Búrquez et al., 2010).
Aerial image processing
Aerial images were obtained using an RGB camera (FC350_3.6_4000x2250 camera, 12 MP, and 96° angle of view), mounted on a UAV (Phantom 3 Advanced, SZ DJI Technology Co, Shenzhen, Guangdong, China). The UAV-RGB system completed 10 missions (automated flights programmed in the Altizure Beta application [Intern at Shenzhen Zhuke Innovation Technology]) to collect image series corresponding to each ground-surveyed site, covering approximately 10 hectares. The missions adhered to the following parameters: a) 90 % frontal and side overlap, b) average altitude of 35 m, c) coverage of approximately 1 hectare of land, and d) initiation around 11:00 AM to avoid shadow effects. Additionally, flight days were selected to ensure minimal cloud cover and winds of no more than 10 km∙h-1.
The images were processed using the photogrammetry software Pix4Dmapper (v 3.1.23, Pix4D SA, Lausanne, Switzerland). This software employs the Structure from Motion and Multi-View Stereo (SfM-MVS) process, which follows the principles of stereoscopic photogrammetry. SfM-MVS automates the extraction of camera parameters from each image in the well-organized array with a high percentage of overlap to obtain the three-dimensional reconstruction of the captured scene (Escalante et al., 2016). It also refines spatial coordinates through an iterative process using non-linear least squares (Westoby et al., 2012). Based on the information from the SfM-MVS process, a point cloud (average density > 4 000 points∙m-2), a digital surface model (DSM), and an orthomosaic image were generated (Navarro et al., 2020; Özyeşil et al., 2017). Additionally, a digital terrain model (DTM) was created by interpolating visible ground points using a k-nearest neighbors’ algorithm with inverse distance weighting (Navarro et al., 2020).
Subsequently, using the raster calculator in ArcMap version 10.1 program (Environmental Systems Research Institute [ESRI], 2011), crown height models (CHM = DSM - DTM) and crown volume models (CVM = CHM * X * Y) were obtained, where X and Y are width and length of the digital model cell, respectively. In conclusion, height and volume data for each individual were extracted from these models.
Estimating vegetation metrics with digital models
From the CHM and CVM, the location and remote metrics of visible individuals from the direct sampling plots were obtained in each orthomosaic. After localization, two approaches were established to obtain the crown area for each individual: manual and automated. The manual approach involved manual digitization; that is, the contour of tree individuals present in the direct sampling plots was delineated using the orthomosaics and the ArcMap program. The second approach, automated, involved using algorithms from the ForestTools package of R program version 0.41.1 (Bartheme et al., 2018), which identifies individuals and segments the crown area using digital height models. Prior to using this tool, it required determining a mathematical function that represented the relationship between crown diameter (twice the radius 1) and height (Navarro et al., 2021), where field data were used to develop the model between these variables. Specifically, ForestTools uses a Variable Window Filter (VWF) for locating individuals based on CHM and the aforementioned mathematical function (Popescu & Wynne, 2013). It also employs a marker-controlled segmentation (MCS) algorithm that takes the output of VWF and the CHM for crown area segmentation, thereby creating an automated digital crown area model.
Having the digital layers of crown area from both manual and automated approaches, vegetation metrics at the individual level were obtained using statistical zone tools such as ArcMap tables. The crown area layers were used to select cells from the digital height and volume models corresponding to each of the trees and shrubs identified in the aerial images. Based on the information separated by individual, the maximum crown height was calculated by identifying the cell with the maximum height value. For crown volume, it was estimated by adding all the volume cells. This process was carried out using the digital crown area layers from each approach.
Estimating aboveground biomass carbon using field-measured vegetation metrics
Based on the vegetation metrics collected in the field, the biomass of trees and shrubs taller than 2 m was estimated using allometric equations at the species and community levels, as described in Table 1. For the dominant species Ipomoea arborescens Sweet and Prosopis velutina Wooton, biomass was calculated using a model constructed from data of individuals of the same species (McClaran et al., 2013; Rojas-García et al., 2015). For Olneya tesota A. Gray, given the similarity between the morphology of this species and P. velutina, the equation of the latter was adjusted using a correction factor of 1.25, representing the proportion of the wood density of Olneya, 0.99 g∙cm-3, relative to Prosopis, 0.79 g∙cm-3 (Silva, 2008). For other species, the non-linear model proposed by Búrquez et al. (2010) was used, which establishes the correlation between crown volume and aboveground biomass of open shrub vegetation. Following the estimation of aboveground biomass, the carbon storage in this reservoir was calculated by applying a conversion factor of 0.47, developed for arid and semiarid vegetation of Mexico, which indicates that 47 % of biomass is carbon (Briones et al., 2018).
Table 1 Allometric equations for estimating aboveground biomass in subtropical shrub communities from field-collected metrics.
| Community or species | Equation | Independent variable | Source |
|---|---|---|---|
| Scrubland | y = 896.501x1.166 | Crown volume (m3) | Búrquez et al. (2010) |
| Ipomoea arborescens Sweet | ln(y) = -4.005 + 2.653(ln x) | Diameter at breast height (cm) | Rojas-García et al. (2015) |
| Prosopis velutina Wooton | ln(y) = [0.67 + 1.55(ln x)] *1.06 | Crown area (m2) | McClaran et al. (2013) |
| Olneya tesota A. Gray | ln(y) = [0.67 + 1.55(ln x) * 1.06] * 1.25 | Crown area (m2) | McClaran et al. (2013) |
Statistical Analysis
The statistical analysis was performed using the Rstudio software version 4.1.1 (R Foundation, 2021) in two stages. The first consisted of the evaluation of the vegetation metrics obtained from the aerial image products, and the second consisted of the construction and evaluation of the ABCS predictive models with these metrics.
Evaluation of vegetation metrics derived from digital models
Crown area, height and volume derived from direct sampling and those estimated from remote sampling (manual digitizing and ForestTools) were analyzed with Shapiro-Wilk tests to determine the normality of the metrics. Because the data did not meet the assumption of normality, non-parametric tests (Wilcoxon Rank-Sum) were performed to determine differences between field estimates and remote approximations. Secondly, the relationship between metrics obtained in the field and with aerial images was analyzed by linear regression, to understand whether those obtained via remote sensing can be used as a proxy for those obtained in situ (Montgomery et al., 2021; Shapiro & Wilk, 1965; Wilcoxon, 1992).
Construction of carbon storage predictive models in aerial biomass
To determine if there is multicollinearity among vegetation metrics obtained from aerial images, a Pearson correlation coefficient (r) analysis and variance inflation factors (VIF) were generated (Lindner et al., 2020). After establishing the presence or absence of collinearity, regression analyses (simple/multiple) were conducted to understand the contribution of variables to explain the variation of carbon storage in aboveground biomass of tree and shrub individuals (Montgomery et al., 2021).
Results and Discussion
Vegetation metrics estimated from field data
In the quadrats established for sampling, 117 trees and shrubs greater than 2 m in height were found, belonging to 13 species (Table 2). In the sites denominated as buffel grasslands, 20 individuals corresponding to four species were recorded, of which O. tesota (eight individuals) and P. velutina (nine individuals) dominated, while for the subtropical scrub, 97 individuals belonging to 10 species were recorded, with I. arborescens (23 individuals) and O. tesota (34 individuals) being the dominant ones. It should be noted that, combining the information from the two communities of interest, the species I. arborescens and O. tesota represent >50 % of the individuals sampled. The trees and shrubs surveyed had crown area ranging from 2.41 m2 to 67.73 m2, maximum crown height between 2.04 m and 6.55 m, and crown volume from 4.93 m3 to 389.15 m3. This natural variation is due to the demographic structure of the populations, the intrinsic differences between the species sampled and the differences in the field (Búrquez et al., 2010; Lai et al., 2022).
Table 2 In Situ vegetation census compared with vegetation censuses obtained with digital layers of crown area by manual digitization (DM) and automated with the ForestTools (FT) algorithm.
| Species | Field data | DM data | FT data |
|---|---|---|---|
| Bursera laxiflora S. Watson | 4 | 2 | 1 |
| Eysenhardtia orthocarpa (A. Gray) S. Watson | 8 | 7 | 6 |
| Fouquieria macdougalii Nash | 7 | 7 | 4 |
| Guaiacum coulteri A. Gray | 1 | 1 | - |
| Ipomoea arborescens Sweet | 23 | 21 | 13 |
| Jatropha cardiophylla (Torr.) Muell. -Arg. | 4 | 2 | 2 |
| Jatropha cordata Müll. Arg. | 12 | 9 | 4 |
| Mimosa laxiflora Benth. | 3 | 1 | 0 |
| Olneya tesota A. Gray | 42 | 36 | 28 |
| Parkinsonia florida (Benth. ex A. Gray) S. Watson | 2 | 2 | 2 |
| Phaulothamnus spinescens A. Gray | 1 | 1 | 1 |
| Prosopis velutina Wooton | 9 | 9 | 9 |
| Vachellia farnesiana (L.) Wight & Arn. | 1 | 1 | 1 |
| Total | 117 | 99 | 71 |
Vegetation metrics estimated with digital models
As a result of the image processing, 10 orthomosaics of 900 m2 were obtained, equally distributed between subtropical scrubland and buffel grassland (five for each vegetation type). Together with each orthomosaic, a DSM and a DTM were also obtained, which correspond to the area of the composite image (orthomosaic). All the digital products mentioned above have a spatial resolution of less than 10 cm. Once the DSM and DTM were obtained, digital models of crown height and volume were generated, which have a similar spatial resolution to the models from which they are derived (<10 cm).
A total of 20 digital crown area layers were generated: 10 corresponding to the manual approximation and 10 derived from the automated approximation. Prior to the generation of the layers with the latter approximation, the relationship between height and crown area diameter was established: Y = X * 1.1066-0.3142 (R2 = 0.64 and P < 0.001), a process necessary to use the VWF algorithm; where Y is crown diameter (m) and X is height (m).
The results with the manual approach suggest that it is possible to locate more than 80 % of the individuals sampled in the field, while with the automated processes it was possible to locate more than 60 % of the individuals (Table 2). Height, crown area and crown volume values were estimated for the 99 individuals obtained with the manual digitization approach and for 71 individuals obtained with the automated approach using ForestTools. The results suggest that the clustering of trees makes their segregation by automated methods difficult (Figure 2) (Navarro et al., 2020; Vivar-Vivar et al., 2022). On the other hand, even though the separation of individuals does not match field surveys, manual digitization suggests that it is possible to recognize and separate a large percentage of them.
Evaluation of vegetation metrics estimated with digital models
To standardize the number of individuals when comparing the efficiency between remote approaches (manual and automated), tree and shrub elements detected commonly in the digital layers were selected. Thus, the analysis includes the use of 45 tree and shrub individuals. As a result of this exercise, the estimated averages for each of the metrics with field data and remote approaches were obtained (Table 3).
Table 3 Vegetation metrics of tree and shrub individuals taller than 2 m in height, obtained in the open field and with remote approaches (manual digitization [DM] and automated with the ForestTools [FT] algorithm) in tropical shrubland communities and induced buffel grassland.
| Attribute | Field data | DM data | FT data |
|---|---|---|---|
| Crown area (m2) | 17.50 ± 14.50 | 19.32 ± 13.12 | 13.93 ± 10.92 |
| Crown height (m2) | 4.51 ± 2.00 | 3.79 ± 1.01 | 3.83 ± 1.04 |
| Volume (m3) | 73.88 ± 99.19 | 82.33 ± 71.35 | 45.36 ± 43.16 |
± standard deviation of the mean.
The metrics analyzed suggest a non-normal distribution, thus the Wilcoxon test was used. For the maximum crown height, the statistical evidence suggests that there is no significant difference between field estimates and both approaches (manual: W = 1 145, P = 0.28; automated: W = 1 127, P = 0.35). Some studies have found that height estimated from aerial imagery shows high and statistically significantly correlation with field data (Gonzalez Musso et al., 2020; Holiaka et al., 2021; Kachamba et al., 2016; Vivar-Vivar et al., 2022). This metric has been used for estimating carbon storage in other plant communities (Holiaka et al., 2021; Kachamba et al., 2016; Navarro et al., 2020).
Estimation of crown area in the field is not significantly different from the manual digitizing approach (W = 1 007, P = 0.96), but it is significantly different from the ForestTools approach (W = 1 278, P = 0.03). Taking into account that crown area measurement is fundamental for the correct estimation of volume and crown height of individuals, results in other studies also suggest that the manual digitizing approach presents data closer to those obtained in the field (Creasy et al., 2021; Holiaka et al., 2021; Gallardo-Salazar & Pompa-García, 2020; Navarro et al., 2020; Vivar-Vivar et al., 2022). However, this difference derives from the approach used, since the automated processes take into account the variability of the crown structure (irregular shapes), while the manual digitization approach and the field approach consider a regular geometric structure. On the other hand, the nature of the aerial images, with both methods, avoids the detection of individuals below the highest canopy layer.
Regarding volume estimations, it was found that field measurements show no significant difference with manual digitization approximations (W = 1 058, P = 0.71), but do differ from the automated approximation (W = 1 393, P = 0.001). Similar to the crown area analysis, these results are attributed to the difference between approximations, as ForestTools estimates volume in irregular crowns (structures built by pixels with spatial resolution <10 cm representing variation in crown strata), while manual digitization estimated figures closer to a regular cylinder (irregular crown area, but only multiplying by maximum crown height, assuming a more orderly construction in crown strata) (Gallardo-Salazar & Pompa-García, 2020).
To evaluate the relationships between remotely sensed vegetation metrics and field measurements, simple linear regression analyses were performed (Figure 3). All metrics showed significant correlation (P < 0.01) and R2 > 0.7 when using the manual approach. On the other hand, the automated approach also showed significant correlation (P < 0.01) for all estimations with R2 > 0.55. This suggests that remote sensing methods can predict morphological attributes measured on the ground with varying degrees of accuracy. Specifically, the results of the present study suggest that estimations via manual digitization represent a tool with potential for the estimation of morphological attributes of individuals in vegetation types where trees and shrubs crowns is visible via aerial images.
Estimation of carbon in aerial biomass with remote vegetation metrics
Predictive models for the estimation of carbon storage in aboveground biomass were generated from remote estimates of vegetation metrics obtained with the manual and automated approaches. Using Pearson's test, it was found that, with the automated approach, crown volume is closely related to crown area (r = 0.95) and crown height (r = 0.81) and, therefore, it is not necessary to include volume in the multiple correlation analysis. It is worth mentioning that this step was omitted for the manual digitization approach, since volume is estimated from the multiplication of crown area and height. The relationship between height and crown area is significantly correlated in the manual (r = 0.63) and automated (r = 0.69) approaches; however, complementing the analysis with VIF (VIF = 1.68 [manual] and VIF = 1.95 [automated]), it was found that the influence of the correlation between these variables represents no high effect in the multiple regression analysis.
Multiple regression analysis (Tables 4) shows that both manual and automated digitization models are statistically significant (P < 0.001). The explanation of the dependent variable (ABCS) in both cases is about 42 % (adjusted R2). According to the degree of significance of the metrics, crown height is the variable that contributes the most in the model. This suggests that, if height is used as an independent variable, the use of simple linear regression models for ABCS prediction would have similar results.
Table 4 Multiple regression analysis for the evaluation of predictive models of aboveground biomass carbon storage. Crown area and height, estimated with the manual (DM) and automated (FT) digitization approaches, were the independent variables.
| Variables | Coefficients | Standard error | T value | Pr(>|t|) |
|---|---|---|---|---|
| DM data | ||||
| Intercept | - 83.53 | 29.97 | -2.78 | <0.001 |
| Crown area | 1.79 | 0.90 | 1.97 | <0.05 |
| Crown height | 27.97 | 9.06 | 3.08 | <0.001 |
| FT data | ||||
| Intercept | - 77.00 | 31.55 | -2.44 | <0.01 |
| Crown area | 1.903 | 1.17 | 1.61 | >0.05 |
| Crown height | 28.05 | 9.74 | 2.87 | <0.001 |
I. arborescens trees were not fitted to the trend line (blue dots, Figure 4). Because of this, the analysis was done with and without this data set. The models generated without taking I. arborescens into account had better fits, explaining the variation in ABCS (Figure 5). The crown area and volume obtained from the manual approach had the best estimation results of ABCS (R2 > 0.7; P < 0.001) for most tree species (Figure 5; Table 5). It may be necessary to conduct exclusive sampling and determine the morphological attributes contributing to the estimation of ABCS for the dominant species I. arborescens.
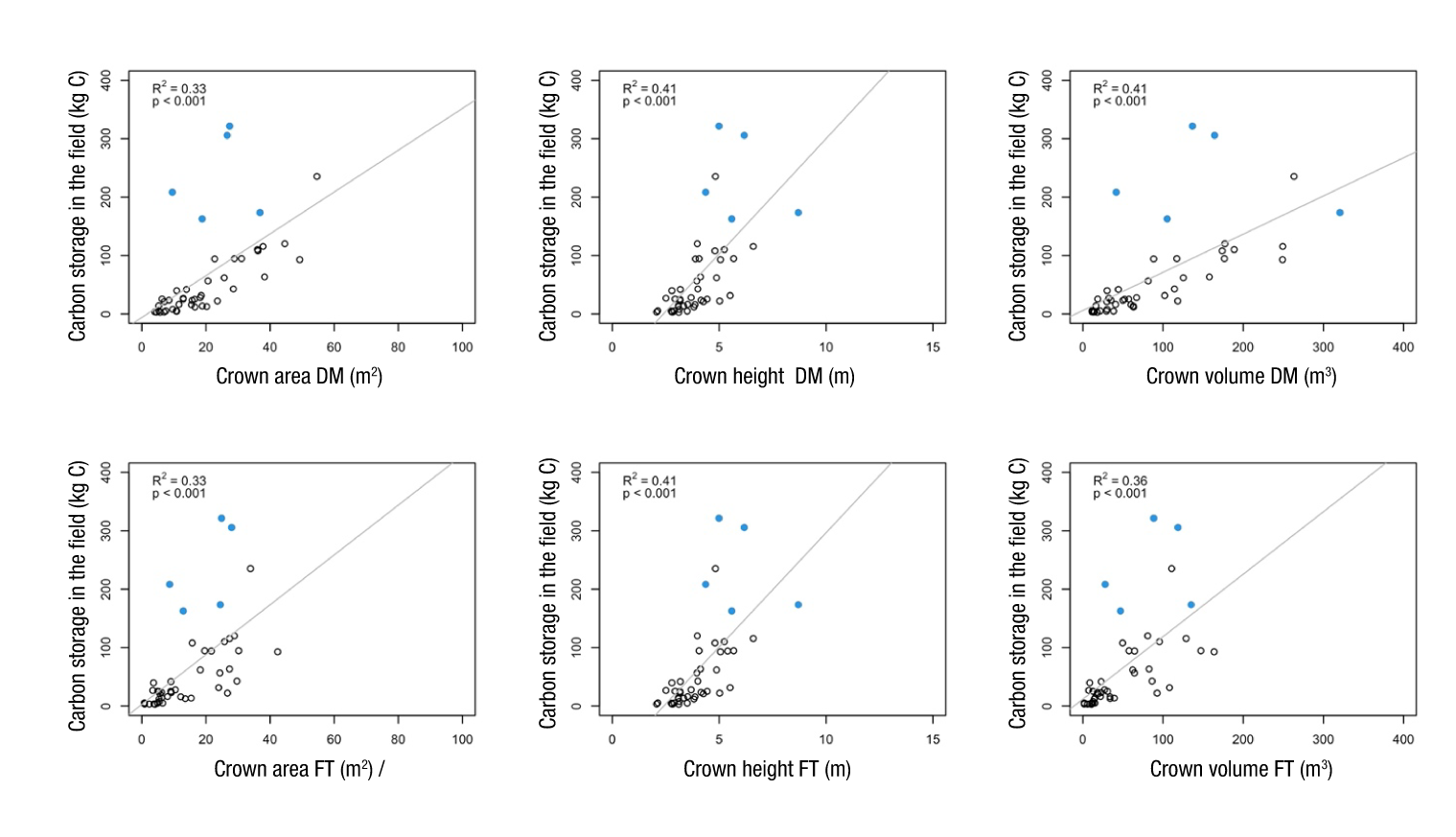
Figure 4 Regression diagrams. The dependent variable is the aboveground biomass carbon storage (individual level) of subtropical shrub communities, and the independent variables are vegetation metrics estimated from aerial images using manual digitization (DM) and automated (FT) approaches. Blue points represent individuals belonging to the species Ipomoea arborescens.
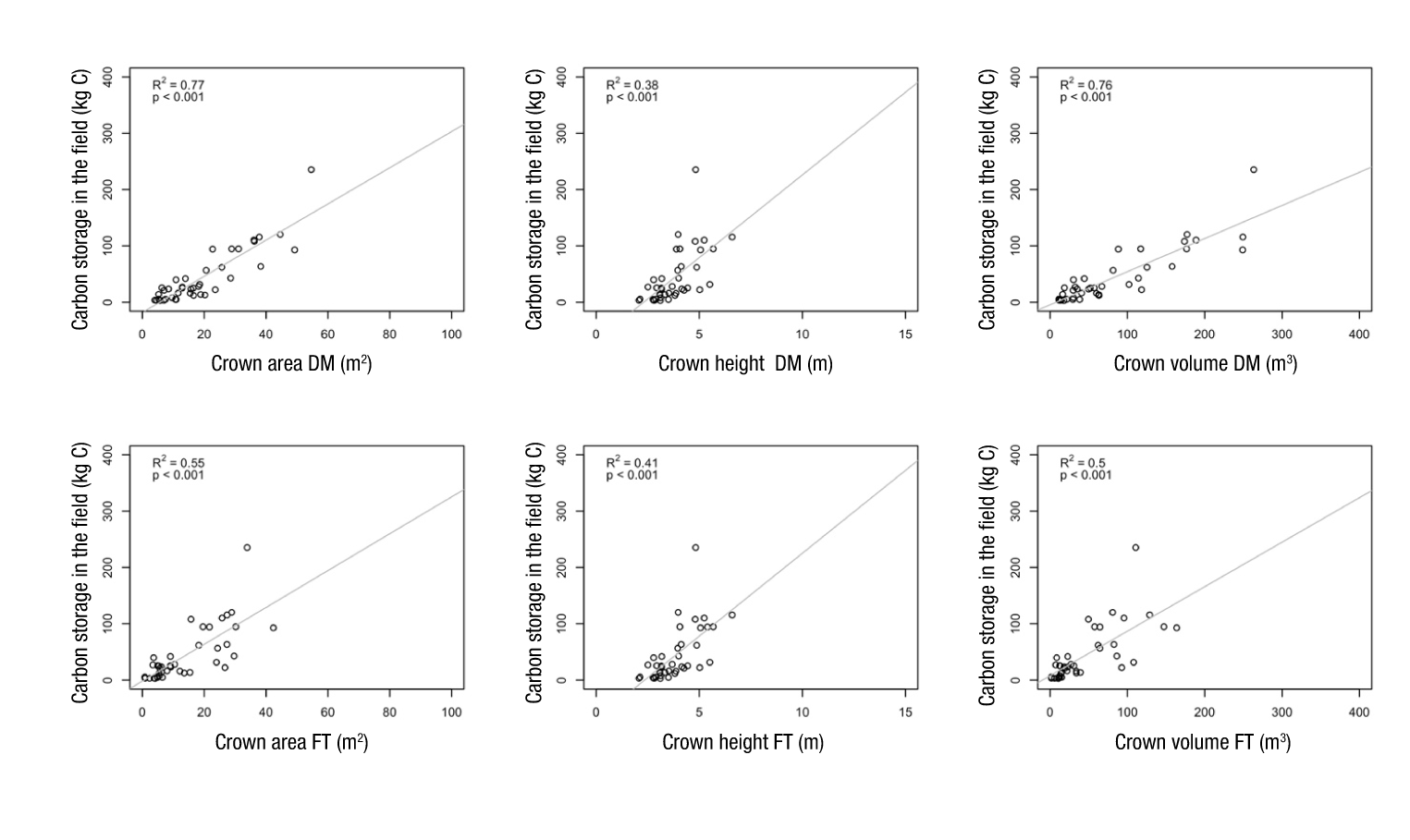
Figure 5 Regression diagrams. The dependent variable is the aboveground biomass carbon storage (individual level) of subtropical shrub communities, excluding the species Ipomoea arborescens. The independent variables are vegetation metrics estimated from aerial images using manual digitization (DM) and automated (FT) approaches.
Table 5 Predictive models of aboveground biomass excluding the species Ipomoea arborescens, where the independent variables were vegetation metrics estimated using manual digitization (DM) and automated approaches (ForestTools algorithms: FT).
| Approach | Metrics | Equation | Standard error | P value | R2 |
|---|---|---|---|---|---|
| DM | Crown area | y = -18.40 + 3.21x | 0.28 | <0.0001 | 0.77 |
| FT | Crown area | y = -1.90 + 3.27x | 0.47 | <0.0001 | 0.55 |
| DM | Height | y = - 67.75 + 29.37x | 6.01 | <0.0001 | 0.38 |
| FT | Height | y = - 69.11 + 29.44x | 5.71 | <0.0001 | 0.41 |
| DM | Volume | y = -4.74 + 0.58x | 0.05 | <0.0001 | 0.76 |
| FT | Volume | y = 7.86 + 0.79x | 0.12 | <0.0001 | 0.50 |
According to field data, on average, the surveyed tree species contain ABCS = 64.88 kg of carbon (Table 6). The multiple regression model with manual digitization data (ABCS = -83.53 + AC*1.79 + AMC*27.93) has an average ABCS of 64.81 kg, while with automated data using ForestTools, the average is ABCS = 64.83 kg (ACBS = -77 + AC*1.90 + AMC*28.05). The ABCS estimates in this study fall within the reported limits in other studies conducted in arid areas (Búrquez et al., 2010; McClaran et al., 2013). When contrasting the ABCS estimation excluding the species I. arborescens, the linear model (crown area as independent variable) indicated that the average ABCS per individual with field data is 43.70 kg, and with manual and automated digitization data, it was 43.63 kg and 43.66 kg, respectively.
Table 6 Values of aboveground biomass carbon storage (ABCS), at the individual tree scale, obtained using manual digitization (DM) and automated (FT) approaches tree in representative subtropical shrub communities in central Sonora.
| Measurements | Data site ABCS (kg) | DM data ABCS (kg) | FT data ABCS (kg) |
|---|---|---|---|
| Mean ± SD | 64.88 ± 78.88 | 64.81 ± 53.50 | 64.83 ± 52.74 |
| Maximum | 321.55 | 225.79 | 213.54 |
| Minimum | 2.82 | 0* | 0* |
*The model yields negative values due to construction. SD: standard deviation.
Because of the use of specific allometric equations for I. arborescens, generalist models may present poor fits (R2 < 0.40 for some models). This derives from the fact that aerial images captured by UAV-mounted cameras do not allow the measurement of the required parameters (e.g. trunk diameter at breast height) for this equation (Creasy et al., 2021; Kachamba et al., 2016; Sun et al., 2021). On the other hand, tree species, whose ABCS estimation depends on metrics measurable via aerial photography (crown area and estimated volume), show good fit between field estimates and measurements via remote sensing. The results suggest that it is possible to generate models that predict the ABCS in arid zones per tree. This is consistent with other works, which show models to calculate ABCS from crown area obtained with RGB-VANT images (Ding et al., 2022; Guo et al., 2021). It should be noted that studies using high-resolution area images for the analysis of carbon storage in arid areas are very limited (Issa et al., 2020), even though these have shown good estimates when contrasted with direct field measurements (Holiaka et al., 2021; Navarro et al., 2020). However, it is necessary to better understand the performance and limitations of these approaches that will be key to integrate them in the study of vegetation structure and ecosystem processes (Sun et al., 2020).
Conclusions
The use of aerial images is a viable and functional source of information for the detection of trees in arid and semi-arid communities to estimate morphological metrics. Based on measurements obtained from an unmanned aerial vehicle (UAV), it was possible to estimate the carbon storage in aerial biomass of trees in subtropical shrubland communities in the arid zones of northwestern Mexico. The development of methodological approaches, such as those proposed in this manuscript, contribute to increase the knowledge of carbon pools in plant communities, which are key in the ecosystem processes of arid zones. New allometric equations are proposed that use morphological metrics obtained with UAV, reducing the intensity/cost of field surveys. This is fundamental in the construction of knowledge for decision making on natural resource management and the establishment of adaptation strategies in the face of climate change.











 texto en
texto en 






