Laelia speciosa (H.B.K.) Schlechter is an endemic Mexican epiphytic orchid in the widespread Neotropical subtribe Laeliinae (van den Berg et al. 2000) widely distributed across the main mountain ranges of the country (Halbinger & Soto-Arenas 1997), with its highest level of abundance in the transversal volcanic belt (Hernández 1992). It grows on individuals of Quercus deserticola Trel. (Halbinger & Soto-Arenas 1997) between 1,200 and 2,400 meters above sea level (McVaugh 1985). While L. speciosa has a relatively large range, it has been extensively extracted from its native habitat by plant sellers and collectors (Ávila-Díaz & Oyama 2002) as well as by local communities that use the flowers in religious ceremonies (Bechtel 1990), and the vegetative structures for the making of traditional crafts (McVaugh 1985, Wiard 1987). In addition to its direct extraction, deforestation has contributed to a reduction in population numbers and recruitment (Hágsater & Soto-Arenas 1998, Hernández 1992, Pérez-Pérez 2003). As a result, most natural populations are very small, consisting of a few scattered individuals. Due to these threats, L. speciosa is listed in the Norma Oficial Mexicana NOM-059-SEMARNAT-2010 under special protection (SEMARNAT 2010) and several programs have been implemented to encourage its protection, ex situ propagation, and sustainable use (Ávila-Díaz & Oyama 2002).
To facilitate conservation efforts in L. speciosa, genetic studies at a variety of scales have been undertaken. At the range-wide scale, isozyme studies have shown high levels of genetic diversity (polymorphic loci = 76 %, Ho = 0.302) (Cole 2003), accompanied with low levels of genetic differentiation among populations (θ p = 0.040), and the presence of private alleles in specific isolated populations using isozymes (Ávila-Díaz & Oyama 2007). At the regional scale within its central area of distribution, analysis with microsatellites also indicates that L. speciosa maintains high levels of genetic diversity (Ho = 0.534 - 0.715) (Rojas-Méndez et al. 2017). While it is known that genetic diversity determined by microsatellite analysis are highly influenced by the type of repeat present in the markers (Merritt et al. 2015) and that cross-species comparisons are more difficult, we can see that L. speciosa maintains population genetic diversity values similar to those found in a variety of other Orchidaceae ranging from the insular epiphytic Vanilla humblotii Rchb. f (Ho = 0.450) (Gigant et al. 2016), to the rare Cymbidium tortisepalum Fukuy. (Ho = 0.619) (Zhao et al. 2017) and the recently reduced in range grassland species Platanthera praeclara Sheviak & M. L. Bowles (Ho = 0.566 - 0.664) (Ross et al. 2013). This high diversity is apparently maintained despite being subjected to high rates of direct exploitation and fragmentation of its habitat (Rojas-Méndez et al. 2017). The presence of inbreeding and evidence indicating recent bottlenecks in selected populations does suggest that habitat fragmentation is having a negative effect on population genetic diversity and structure and that more extensive conservation measures should be implemented.
Conservation strategies need to focus on both maintaining levels of genetic diversity and preserving private alleles of potentially adaptive or evolutionary significance. To meet this goal, extraction must be kept to a minimum and reintroductions should take place from individuals within close proximity (Ávila-Díaz & Oyama 2007, Rojas-Méndez et al. 2017).
While these studies have provided important information regarding patterns of genetic diversity, they have not specifically addressed L. speciosa’s epiphytic habit. The spatially complex epiphytic habit and the spatial correlation of individuals within it are likely important for persistence and conservation of genetic diversity in individual populations due to the potential for closer interaction among individuals for both pollination and seed dispersal than what is seen in terrestrial species (Diniz-Filho & Telles 2002, Escudero et al. 2003, Trapnell et al. 2004, Chung et al. 2005b).
Even though about 10 % of all vascular plants show an epiphytic habit, there are few genetic studies available on these species which could give insight into how the epiphytic habit controls genetic diversity and structure (González-Astorga et al. 2004). For orchids which are often epiphytic, only a handful of species have been studied genetically in light of their epiphytic habit, including Brassavola nodosa Lindl. (Trapnell et al. 2013), Broughtonia cubensis Cogn. (Raventós et al. 2011), Catasetum viridiflavum Hook. (Murren 2003), Cattleya labiata Lindl. (Pinheiro et al. 2012), Laelia rubescens Lindl. (Trapnell et al. 2004) and Vanilla humblotii. (Gigant et al. 2016). Of these studies, only Trapnell et al. (2004) examined fine-scale structure with high detail (i.e., sampling of all individuals within a tree host) showing significant patterns of relatedness at distances of less than 45 cm, likely due to a combination of vegetative reproduction and sexually derived offspring resulting from localized seed dispersal.
Within any plant population, two main factors, restricted movement of pollen and seed dispersal, could lead to the presence of a fine-scale genetic structure where genetic variation among individuals is nonrandom (Loveless & Hamrick 1984, McCauley 1997, Chung et al. 2005a, Dick 2008). Other factors including selection, historical events, genetic drift, isolation in small patches, clonal reproduction, and mating systems may also play a less important role in favoring specific genetic structure (Hamrick & Nason 1996, Hardy & Vekemans 1999, Kalisz et al. 2001, Vekemans & Hardy 2004, Chung et al. 2005a).
In the Orchidaceae, wind mediated seed dispersal allows for long-distance dispersal (Arditti & Ghani 2000). Theoretically, this could limit the contribution of localized seed dispersal to the fine-scale genetic structure, suggesting that pollen movement will be the main factor contributing to localized genetic structure in orchids. However, several studies have shown that limited seed dispersal is in fact common in orchids and contributes largely to the fine-scale genetic structure of populations (Peakall & Beattie 1996, Machon et al. 2003, Trapnell et al. 2004, Jacquemyn et al. 2006). It has also been observed that non-rewarding species, such as L. speciosa, show less genetic differentiation among populations (due to increased movement of pollinators among patches) than rewarding species (since pollinators will stay in the same patch visiting flowers) and therefore will not show a strong fine-scale genetic structure (Cozzolino & Widmer 2005, Tremblay et al. 2005).
Since epiphytic species have a three-dimensional arrangement within a tree canopy, the fine-scale genetic structure of these species will also have a three-dimensional component. A horizontal structure will be present if there is a higher level of genetic relatedness among individuals in the same vertical strata of the tree, while a vertical structure will be present if there is a higher level of genetic relatedness among individuals on different branches in different strata (Trapnell et al. 2004).
In addition to considering genetic structure in terms of spatial arrangement, examining individuals occurring in different cohorts and/or life stages could allow for detection of changes in genetic structure from class to class, potentially allowing for the inference of ecological and life history causes of this structure, which could then be applied to conservation programs (Kalisz et al. 2001, Chung et al. 2003a, Octavio-Aguilar et al. 2017). Several studies have noted either a decrease (Hamrick et al. 1993, Epperson & Alvarez-Buylla 1997, Parker et al. 2001, Chung et al. 2003a) or an increase (Eguiarte et al. 1992, Tonsor et al. 1993, Cabin 1996, Kalisz et al. 2001, Kittelson & Maron 2001, Chung et al. 2005a, Jacquemyn et al. 2006) in genetic structure as life-stages progress. A decrease in fine-scale genetic structure from seedlings to adults is generally explained by high mortality rates at early stages, while increases in genetic structure is explained by historical factors such as founder events and local selection, while isolation by distance processes (i.e. limited pollen or seed dispersal) help maintain genetic structure across age classes (Chung et al. 2003a, Tero et al. 2005, Jacquemyn et al. 2006). Despite the obvious implications of age class or cohort differences to overall genetic structure, few studies have examined genetic structure in this way (Eguiarte et al. 1992, Hamrick et al. 1993, Tonsor et al. 1993, Cabin 1996, Epperson & Alvarez-Buylla 1997, Chung et al. 2000, Kalisz et al. 2001, Kittelson & Maron 2001, Parker et al. 2001, Chung et al. 2003a, Tero et al. 2005, Jacquemyn et al. 2006), and of those that have, none have specifically focused on epiphytic species.
To investigate this pattern of genetic partitioning we used microsatellite markers to evaluate the fine-scale genetic structure among all individuals in two populations, with populations being defined as individual trees, containing L. speciosa to address the following questions:
(i) How is genetic diversity maintained within individual trees and are these trees representative of the full population? (ii) Does the epiphytic habitat affect the fine-scale genetic structure of individual tree-level populations and is that pattern consistent across different age classes? (iii) What are the implications for conservation and restoration of L. speciosa given the observed patterns of diversity and fine-scale genetic structure?
Materials and methods
Study site. Field work was conducted in the spring of 2006 on Cerro el Agostadero in the municipality of Caurio de Guadalupe in Michoacán, Mexico at 2,327m above sea level. This area is a large undisturbed fragment of Quercus deserticola forest and L. speciosa is the dominant epiphytic orchid (Pérez-Pérez 2003). We chose this location as previous studies (Medina 2004, Pérez-Pérez 2003) and field observations (Ávila-Díaz pers. comm.) concluded that this forest patch supports the largest and most well-preserved population of L. speciosa across its range. The forest is relatively hard to access and therefore locals do not use this area for orchid extraction; the only human use of the land is the occasional occurrence of cattle which enter the forest from cleared grazing lands on the mountain’s lower slopes.
We selected two trees separated by approximately 100 m that did not include any other epiphytic orchids either within their canopies or within the canopies of adjacent trees for sampling with each tree considered an individual population.
Data collection. Within the two selected trees, we mapped all individuals of L. speciosa in X, Y, Z coordinate space, where X and Y represent canopy width and depth, while Z represents height by measuring plant height above the ground, angle of the branch in which they were growing and the distance from the center of the tree and their relative position around the center of the trunk (Figure 1).

Figure 1 A. Single individual tree of Quercus deserticola supporting one of the two sampled populations of Laelia speciosa with the second author sampling plants. B. Branch supporting multiple individuals of Laelia speciosa showing the pattern of pseudobulb development. C. Large flowering individual of Laelia speciosa.
Laelia speciosa grows by the production of globular-ovoid pseudobulbs with only one pseudobulb produced each year (Hernández 1992, Pérez-Pérez 2003) (Figure 1). Since the number of pseudobulbs is a good estimator of plant age, previous demographic studies have used pseudobulb number to identify distinct life history stages (Hernández 1992). Following this system of classification, individuals were grouped into one of four age classes: Seedlings (individuals with 1 pseudobulb), Juveniles (2-10 pseudobulbs), Adults I (11-20 pseudobulbs) and Adults II (21 or more pseudobulbs).
From all individuals, a portion of a single leaf was collected for genetic analysis. In rare occasions, one cluster of pseduobulbs will appear to have more than one front of growth, suggesting the presence of multiple individuals or to alterations in the meristematic region. In these cases, all leaves were collected to later determine if the cluster of pseudobulbs represented one or more individuals.
Microsatellite analysis. Samples were collected on ice and frozen within a few hours of collecting at -80 °C. DNA was extracted using the DNeasy® Plant Mini Kit (QIAGEN, Hilden, Germany).
Six microsatellite primers (Lspe-1, Lspe-2, Lspe-3, Lspe-5, Lspe-9 and Lspe-10) previously described for L. speciosa (Cortés-Palomec et al. 2008) were used to genotype all individuals in the populations. Multiplex PCR and resultant fragment analysis was performed as described in Cortés-Palomec et al. (2008).
Descriptive statistics. We tested for the presence of null alleles, upper-allele dropout, and errors due to stuttering using MICRO-CHECKER ver. 2.2.3 (Van Oosterhout et al. 2004) with 102 bootstrap simulations and a 95 % confidence interval. The proportion of polymorphic loci (P), total number of alleles (A), mean number of alleles per locus (Ā), number of private alleles (Np), observed (Ho) and expected (He) heterozygosity, and the fixation index (F) were estimated using the program GENETIC DATA ANALYSIS (GDA) ver. 1.0 (Lewis & Zaykin 2001). These parameters were estimated singly for each age class in each tree and for all pooled individuals. 95 % confidence intervals of F values were calculated using 1,000 permutations. An Analysis of Molecular Variance (AMOVA) was performed to test for genetic differences between the two trees and among the four age classes within each tree using the program ARLEQUIN ver. 3.1 (Excoffier et al. 2005).
Since microsatellite markers have high rates of mutation and are more likely to follow a stepwise mutation model than an infinite alleles model, it has been suggested that RST values would be more appropriate to analyze microsatellite data than FST (Lowe et al. 2004). However, RST has been shown to be less accurate when population samples are large, or when less than 10 loci are used (Lowe et al. 2004). For these reasons, we decided to use a more traditional approach and analyze our data using Wright’s (1965)F-statistics (FIS, FIT and FST), where FIS measures deviations from H-W equilibrium within individuals in each size class, FST measures deviations from H-W equilibrium among age classes, and FIT measures deviations within the entire population, and were calculated following Weir & Cockerman’s (1984) multilocus estimators in a global fashion using the program FSTAT ver. 2.9.3. (Goudet 2001). The significance of the F-statistics was tested based on 1,000 permutations of alleles. Means and standard errors were obtained by jackknifing over polymorphic loci, bootstrap confidence intervals (CI = 95 %) were constructed around jackknifed means of the F-statistics and means were considered significant when confidence intervals did not overlap zero.
To evaluate the potential impact of selfing on population structure, selfing rates were estimated using the method implemented in REMS (Robust Multilocus Estimate of Selfing, David et al. 2007) based on maximizing the likelihood of the observed distribution of multilocus heterozygosity. This method has been shown to be very robust for determining selfing rates in light of issues with microsatellite data, including potential null alleles or partial dominance. Using a precision of 0.0001, we calculated selfing rates (s) along with the 95 % CI for each size class in each tree. To account for differences in sample size that could affect the selfing rate estimate, we calculated s for the full population and for equal-sized subsets randomly chosen from the full population (9 individuals for Tree 1 and 17 individuals for Tree 2).
Spatial correlation analyses. Several methods are available to calculate spatial correlation (Escudero et al. 2003, Heywood 1991) including Moran’s I (Sokal & Oden 1978), and the “sp-statistics” (Hardy & Vekemans 2002). A measure of coancestry can be calculated by estimating the probability that genes in different individuals within subpopulations are identical by descent (Loiselle et al. 1995). A kinship coefficient or coefficient of coancestry (fij) was calculated using the program fij ANAL3D designed by J. D. Nason (Iowa State University). This program uses an algorithm with a multilocus approach to calculate the correlation of the frequencies of homologous alleles at a locus in pairs of mapped individuals over a range of distance intervals and it was designed to support three-dimensional data (Loiselle et al. 1995, Kalisz et al. 2001, Franks et al. 2004, Trapnell et al. 2004). Distance intervals of 5 cm were assigned since field observations revealed high densities of L. speciosa in most branches with multiple individuals occurring within this distance interval. Additionally, this conservative distance interval was assigned on the basis that the larger the distance interval the smaller the confidence around the estimated fij value increasing the odds of missing the fine-scale genetic structure (Chung et al. 2003b). A randomization procedure was used to test the null hypothesis of no spatial genetic structuring (fij = 0) of the sample population based on N-1 = 399 simulation trials and α = 0.05, constructing a 95 % confidence interval. Negative values of fij indicate that the individuals are less related than expected by chance while positive values indicate relatedness at a level more than expected by chance (Chung et al. 2003b). Under the assumption of no inbreeding and no spatial genetic structure, fij values of 0.25 represent full-sib progeny and 0.125 half-sib progeny (Kalisz et al. 2001, Trapnell et al. 2004).
Results
Tests for scoring errors due to stuttering or large allele dropout were negative across all combinations of sample and locus. Excess homozygosity suggesting the presence of null alleles was seen in loci Lspe-5 and Lspe-9 in particular size classes and trees. However, these patterns were inconsistent, and for this reason no loci or populations were removed from the analysis.
A total of 178 and 276 different individuals of L. speciosa were found on Tree 1 and Tree 2 respectively, and all individuals represented distinct genets (Table 1). All the sampled individuals were evenly distributed throughout the branches in the canopy (Figure 2). In both trees, the age class with the largest number of individuals was Juveniles (2-10 years old), representing 49 % of all individuals in Tree 1 and 43 % in Tree 2, followed by Adults I (11-20 years old) representing 40 % of all individuals in Tree 1 and 34 % in Tree 2, Seedlings (less than two years old), representing 6 % of all individuals in Tree 1 and 17 % in Tree 2, and lastly Adults II (over 20 years old) representing 5 % of all individuals in Tree 1 and 6 % in Tree 2 (Table 1). The oldest individual sampled was 33 years old. Of the total number of clusters sampled that showed more than one front of growth, the majority corresponded to the occurrence of multiple individuals growing together and not a division of the meristem. In Tree 1, of the 19 clusters of pseudobulbs with more than one front of growth, 15 corresponded to more than one genotype. In Tree 2 a similar pattern was found and of the 38 clusters 28 had more than one genotype (Table 2). The number of genetically different individuals in those clusters was variable, with the largest cluster (5 fronts of growth) corresponding to 2 different individuals (Table 2). All individuals that were identified as such in the field were included in the analysis. For those clusters in which it was hard to tell whether there was more than one individual involved, we used the genetic determination and included only genetically different individuals in the final genetic analysis using the same geographic coordinate for the multiple individuals sampled from the same cluster.
Table 1 Summary of microsatellite variation and mean F-values observed in two populations of Laelia speciosa and four age classes. Sample size (N), Proportion of polymorphic loci (P), Total number of alleles (A), Mean number of alleles per locus (Ā), Number of private alleles (Np), Expected Heterozygosity (He), Observed Heterozygosity (Ho), and Fixation index (F). Seedlings correspond to individuals less than 2 years old, Juveniles: 3-10 years old, Adults I: 11-20 years, and Adults II individuals older than 20 years. * Significant deficit of heterozygosity across polymorphic loci.
| N | P | A | Ā | Np | He | Ho | F (95 % CI) | |
|---|---|---|---|---|---|---|---|---|
| Tree 1 All individuals | 178 | 1 | 57 | 9.5 | 2 | 0.607 | 0.490 | 0.188 (-0.035, 0.475) |
| Seedlings | 10 | 1 | 27 | 4.5 | 0 | 0.592 | 0.487 | 0.184 (-0.076, 0.447) |
| Juveniles | 87 | 1 | 50 | 8.3 | 1 | 0.611 | 0.506 | 0.173 (-0.066, 0.466) |
| Adults I | 72 | 1 | 52 | 8.6 | 1 | 0.602 | 0.490 | 0.186 (-0.042, 0.475) |
| Adults II | 9 | 1 | 28 | 4.6 | 0 | 0.612 | 0.398 | 0.360 (0.071, 0.095)* |
| Tree 2 All individuals | 276 | 1 | 64 | 10.7 | 6 | 0.577 | 0.480 | 0.169 (-0.042, 0.443) |
| Seedlings | 46 | 1 | 44 | 7.3 | 3 | 0.590 | 0.474 | 0.197 (-0.012, 0.528) |
| Juveniles | 119 | 1 | 52 | 8.6 | 2 | 0.577 | 0.501 | 0.131 (-0.080,0.386) |
| Adults I | 94 | 1 | 51 | 8.5 | 1 | 0.564 | 0.469 | 0.168 (-0.03, 0.436) |
| Adults II | 17 | 1 | 27 | 4.5 | 0 | 0.551 | 0.402 | 0.275 (0.008, 0.538)* |
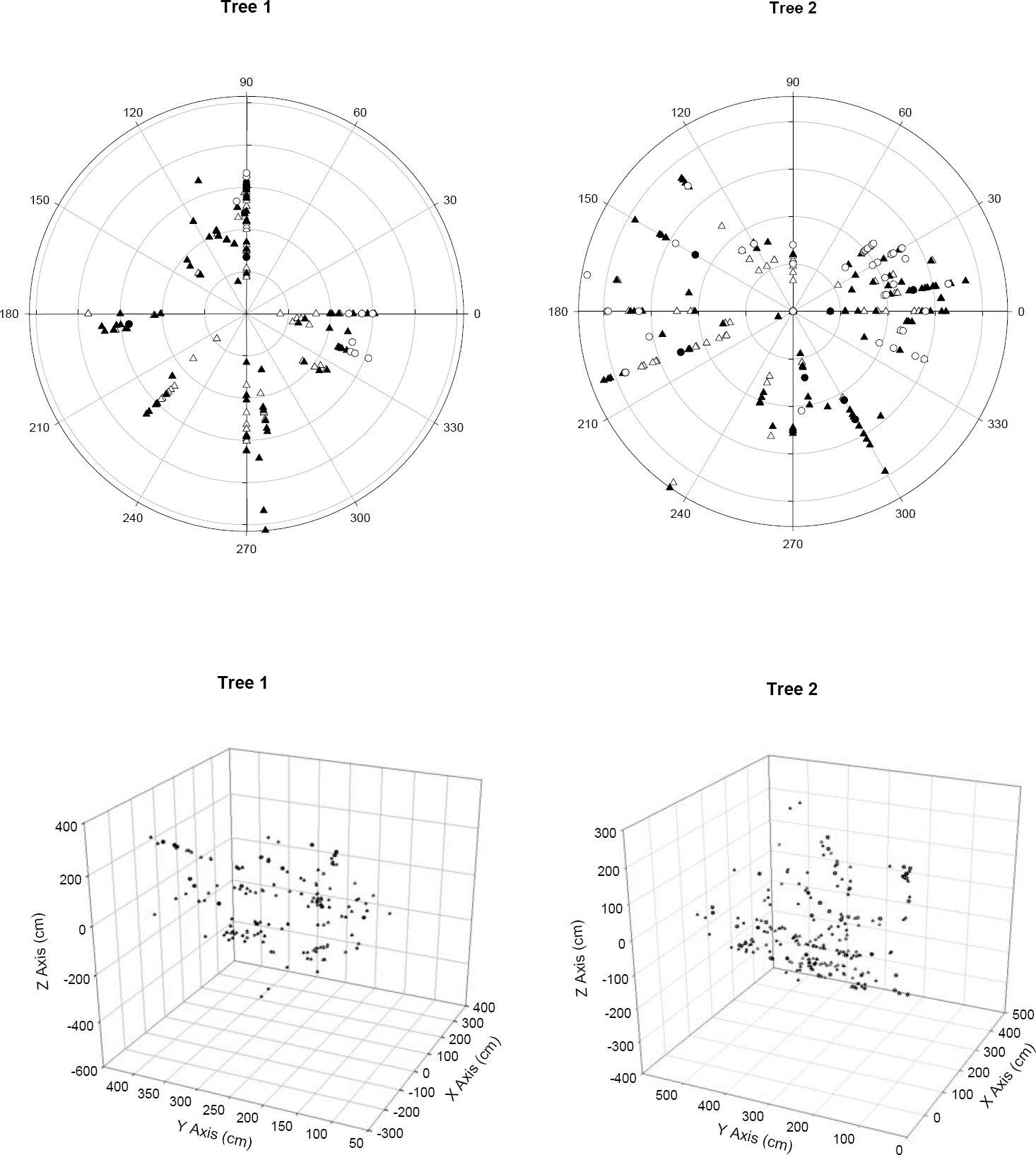
Figure 2 Spatial distribution of Laelia speciosa individuals within the canopy of Quercus deserticola in two populations (trees). Seedlings (○), Juveniles (▲), Adults I (∆), Adults II (●). Top: Polar view. Bottom: Three dimensional views.
Table 2 Frequency of individuals of Laelia speciosa with more than one front of growth in the populations. The number of fronts (N), number of patches with this pattern (n) and the number of times that this corresponded to one genotype (G = 1), two genotypes (G = 2), three genotypes (G = 3) is included.
| Tree 1 | Tree 2 | ||||||||
| Number of fronts, N | 5 | 4 | 3 | 2 | Number of fronts, N | 5 | 4 | 3 | 2 |
| Number of Patches, n | 0 | 1 | 2 | 16 | Number Patches, n | 1 | 2 | 10 | 25 |
| G = 1 | 0 | 0 | 0 | 4 | G = 1 | 0 | 0 | 1 | 9 |
| G = 2 | 0 | 0 | 2 | 12 | G = 2 | 1 | 1 | 5 | 16 |
| G = 3 | 0 | 1 | 0 | 0 | G = 3 | 0 | 1 | 4 | 0 |
Genetic diversity and structure. High levels of genetic variation and polymorphism were observed in the two single-tree populations studied (Table 1). A total of 71 alleles were found across the six loci (27 in Lspe-1, 10 in Lspe-2, 12 in Lspe-3, 6 in Lspe-5, 9 in Lspe-9, and 7 in Lspe-10) with all loci polymorphic across the two trees. Private alleles were found in both trees at a low percentage (3.5 % of total in Tree 1 and 9.3 % of total in Tree 2) (Table 1) and were generally found in size classes having a larger number of individuals. A significant deficit of heterozygotes was found at Lspe-2, Lspe-5, and Lspe- 9 in Tree 1 with Lspe-1 additionally showing a similar pattern in Tree 2, both for FIS (within age classes) and FIT (over all samples) values. The other loci did not deviate from H-W expectations.
Non-significant differences in allelic frequencies were found among age classes (FST) in Tree 1, in contrast in Tree 2 we found significant differences in 4 loci (Lspe-1, Lspe-2, Lspe-3 and Lspe- 9), and the confidence intervals (95 % CI) indicated that the mean differentiation among classes was significantly different than zero (Table 3). The bootstrap confidence limits (CI = 95 %) around the fixation index (F) showed a significant deficit of heterozygosity in Adults II for both trees (Table 1), while in the other age classes and when all individuals were pooled together it was not significant. The multilocus test did not reveal significant levels of deficit of heterozygosity at either level (Table 3). The estimated mean inbreeding coefficient (FIS) across loci was similar for both trees (0.185 for Tree 1 and 0.164 for Tree 2). The analysis of selfing, determined through examining the likelihood of the observed distribution of multilocus heterozygosity, indicated some selfing in both trees. The highest levels of selfing (30.3 %) was found in the oldest size class in Tree 1 (Table 4).
Table 3 F-statistics following the method of Weir & Cockerham (1984) and P-values (test at Ho = 0) for six polymorphic loci from all age classes of Laelia speciosa in two trees. N = Number of alleles.
| Locus | N | FIS | P | FIT | P | FST | P | |
|---|---|---|---|---|---|---|---|---|
| Tree 1 | Lspe-1 | 24 | 0.013 | 0.340 | 0.009 | 0.352 | -0.004 | 0.180 |
| Lspe-10 | 4 | -0.298 | 0.999 | -0.297 | 0.999 | 0.000 | 0.536 | |
| Lspe-2 | 8 | 0.093 | 0.025 | 0.095 | 0.024 | 0.003 | 0.906 | |
| Lspe-3 | 11 | 0.018 | 0.308 | 0.016 | 0.327 | -0.002 | 0.721 | |
| Lspe-5 | 4 | 0.889 | 0.001 | 0.885 | 0.001 | -0.032 | 0.910 | |
| Lspe-9 | 6 | 0.642 | 0.001 | 0.646 | 0.001 | 0.013 | 0.240 | |
| Mean (SE) | 0.185 (0.148) | 0.186 (0.150) | -0.000 (0.004) | |||||
| 95 % CI | -0.034, 0.473 | -0.036, 0.470 | -0.009, 0.007 | |||||
| Tree 2 | Lspe-1 | 26 | 0.084 | 0.001 | 0.087 | 0.001 | 0.003 | 0.013 |
| Lspe-10 | 5 | -0.278 | 0.999 | -0.280 | 0.999 | -0.002 | 0.252 | |
| Lspe-2 | 8 | 0.160 | 0.001 | 0.174 | 0.001 | 0.017 | 0.019 | |
| Lspe-3 | 12 | -0.022 | 0.826 | -0.013 | 0.681 | 0.009 | 0.001 | |
| Lspe-5 | 5 | 0.796 | 0.001 | 0.795 | 0.001 | -0.007 | 0.242 | |
| Lspe-9 | 8 | 0.613 | 0.001 | 0.620 | 0.001 | 0.018 | 0.007 | |
| Mean (SE) | 0.164 (0.137) | 0.172 (0.138) | 0.009 (0.003) | |||||
| 95 % CI | -0.048, 0.427 | -0.039, 0.435 | 0.003, 0.015 |
Table 4 Estimation of selfing rate s by age class in two single-tree populations of Laelia speciosa. Selfing rate was estimated using a maximum likelihood method implemented in the software package REMS (Robust Multilocus Estimate of Selfing). The potential influence of sample size on selfing rate was evaluated by computing s for both the full population size and for a randomly selected subset of individuals matching the sample size of the least abundant size class.
| N | s | 95 % CI | |
|---|---|---|---|
| Tree 1 | |||
| Seedlings | 10 | 0.200 | (0.023, 0.497) |
| 9 | 0.241 | (0.027, 0.547) | |
| Juveniles | 87 | 0.060 | (0, 0.163) |
| 9 | 0 | (0, 0.516) | |
| Adults I | 72 | 0.039 | (0, 0.142) |
| 9 | 0.210 | (0.016, 0.448) | |
| Adults II | 9 | 0.304 | (0, 0.566) |
| 9 | 0.310 | (0, 0.566) | |
| Tree 2 | |||
| Seedlings | 46 | 0.121 | (0, 0.235) |
| 17 | 0.119 | (0, 0.316) | |
| Juveniles | 119 | 0.016 | (0, 0.116) |
| 17 | 0 | (0, 0175) | |
| Adults I | 94 | 0 | (0, 0.104) |
| 17 | 0 | (0, 0.216) | |
| Adults II | 17 | 0 | (0, 0.183) |
| 17 | 0 | (0, 0.183) |
Differentiation between the two trees using AMOVA indicated that only 1 % of the genetic variance can be attributed to differences between trees and that there were no genetically significant differences among age classes (data not shown).
Three-dimensional spatial correlation analyses. Our analyses indicated a significant genetic structure in both populations (trees) studied. The maximum values of the coefficient of coancestry (fij) were 0.184 for Tree 1 (Table 5) and 0.212 and Tree 2 (Table 6) when all individuals in the tree were analyzed together. When the analysis was performed among different age classes, the fij values for Juveniles were 0.244 and 0.122 for Tree 1 and 2 respectively, and 0.129 and 0.230 for Adults I (Table 5 and 6). For Adults II, only individuals in Tree 2 showed a significant genetic structure with a fij value of 0.429 (Table 6). The values of fij observed in Tree 1 for all individuals and Adults I were close to the fij values expected for half-sibs (0.125), while in the Juveniles the fij was closer to those found in full-sibs (0.25) (Table 5). In Tree 2, on the other hand, the values of fij observed for all individuals, Adults I and Adults II were closer to those of full-sibs, while Juveniles behaved like half-sibs (Table 6).
Table 5 Kinship coefficient values (fij) for the shortest distance intervals in Tree 1 in four age class categories. (*significant values at α = 0.05)
| Distance interval (cm) | Tree 1 All individuals | Seedlings | Juveniles | Adults I | Adults II |
|---|---|---|---|---|---|
| 5 | 0.184* | - | 0.244* | 0.129* | 0.015 |
| 10 | 0.086* | - | 0.111* | 0.028 | - |
| 15 | 0.035* | -0.026 | 0.091* | -0.001 | - |
| 20 | 0.068* | - | 0.036 | 0.042 | 0.023 |
| 25 | 0.041* | 0.05 | 0.023 | -0.012 | - |
| 30 | 0.0002 | - | 0.045 | -0.048 | - |
| 35 | -0.004 | - | 0.012 | 0.017 | - |
Table 6 Kinship coefficient values (fij) for the shortest distance intervals in Tree 2 in four age class categories. (*significant values at α = 0.05)
| Distance interval (cm) | Tree 2 All individuals | Seedlings | Juveniles | Adults I | Adults II |
|---|---|---|---|---|---|
| 5 | 0.212* | 0.016 | 0.122* | 0.230* | 0.429* |
| 10 | 0.097* | -0.024 | 0.075* | 0.151* | - |
| 15 | 0.058* | 0.033 | 0.012 | 0.096* | - |
| 20 | 0.043* | 0.063 | 0.124 | 0.031 | - |
| 25 | 0.017 | 0.059 | 0.042 | 0.007 | - |
| 30 | -0.008 | -0.002 | -0.037 | 0.040 | -0.235 |
| 35 | 0.004 | 0.066 | -0.002 | 0.006 | - |
When considering all individuals in Tree 1 in the analysis, a significant genetic structure (α = 0.05) was found among individuals located up to 25 cm (Table 5), while in Tree 2 there was a significant structure among individuals located up to 20 cm (Table 6). When the analysis was performed in the four different age class categories, we did not find any structure among the seedlings in any tree. However, as we moved up in the age classes, we found a significant structure among Juveniles up to 15 cm in Tree 1 and 10 cm in Tree 2; while in Adults I there was a significant structure among individuals located up to 5 cm in Tree 1 and up to 15 cm in Tree 2 (Table 5 and 6; Figure 3). Only in Tree 2 was there a significant structure in Adults II in the first distance class (5 cm). The occasional presence of significant coancestry values, either positive or negative, in a few of the correlograms at much larger distance intervals (Figure 3), with no trend in the estimates at neighboring distance classes wasprobably due to chance and were not considered of biological importance, but rather an artifact of the analysis (Loiselle et al. 1995, Kalisz et al. 2001).
Discussion
Genetic Diversity. Previous work with L. speciosa had shown the species to maintain relatively high levels of genetic diversity across its range (Ávila-Díaz & Oyama 2007, Rojas-Méndez et al. 2017), and our study reinforces this finding and shows that even at the single tree level, a large proportion of the diversity seen in populations is maintained in individual trees.
High levels of genetic variation (Ho = 0.490 (Tree 1) and 0.480 (Tree 2)) were found in the two single-tree populations of L. speciosa analyzed, a reduction by a factor of 1.46 from a population-wide assessment of diversity (Ho = 0.714) using the same microsatellite methods (Rojas-Méndez et al. 2017) (Table 1). The similarity of total diversity and the lack of differentiation between the trees as shown through AMOVA, shows that these are representative of the diversity found within the orchid meta-population within the continuous forest of Q. deserticola. Within this highly conserved population of L. speciosa, we see genetic patterns congruent with a dynamic process of widespread pollination and seed dispersal across the meta-population with consistent gene flow and colonization from a variety of individuals.
Private alleles were found in individual trees and size classes, but tended to correlate with sample size. While private alleles have been identified at the range level in L. speciosa associated with specific geographic regions (Ávila-Díaz & Oyama 2007), the variation seen here is probably related to the high genetic diversity exhibited by the SSR markers and is not likely to be adaptive.
Tree-level age-class distribution and fine-scale genetic structure. We found an uneven distribution of individuals among different age classes in L. speciosa, with the Juvenile and Adults I classes accounting for most individuals in both trees. This indicates that most plants in the population were not reproductive, in accordance with Hernández (1992) who noted that up to 85 % of all plants sampled in her demographic study were non-reproductive individuals, younger than 12 years old. While there were large differences in numbers of individuals among different age classes, there was no significant genetic differentiation among these classes as determined through AMOVA. In contrast, F statistics, particularly FST, did indicate some variation and low but significant differentiation among age classes (FST = 0.009), particularly in Tree 2 (Table 3). The contrasting conclusions of the two analyses are likely due to the differences in population numbers between the two single-tree populations. We therefore believe that recruitment of new individuals in each tree appears to be following similar patterns throughout time.
Laelia speciosa showed a significant positive genetic structure when all individuals were pooled together, and in the Juvenile and Adults I age classes in both trees despite differences in the total number of individuals (276 individuals in tree 2 vs. 178 individuals in tree 1). Additionally, a significant genetic structure was found in Adults II for Tree 2. No fine-scale genetic structure was found in the Seedling category in any tree. The distance interval at which we found fine-scale genetic diversity (up to 25 cm) was small compared to that found in terrestrial orchids. For instance, Chung et al. (1998) found a significant genetic structure in the terrestrial orchid Cymbidium goeringii (Rchb.f.) Rchb.f. at distances of 3 m., while in Orchis cyclochila Maxim. there was structure in individuals separated less than 1 m (Chung et al. 2005a). However, our values are more similar to those found in the epiphytic orchid Laelia rubescens, in which there was fine-scale genetic structure in individuals separated up to 45 cm (Trapnell et al. 2004).
While the overall pooled genetic structure was similar between the two trees, there were some differences in the pattern and select size classes. The largest fij value was closer to those of half sibs in Tree 1 (0.184) and full sibs (0.212) in Tree 2. This pattern was inconsistent between the two trees, with the Juvenile size class in Tree 1 indicating full sibs (0.244) and Tree 2 half-sibs (0.122), while in Adults I the fij values suggested half sibs (0.129) in Tree 1 and full-sibs (0.230) in Tree 2. Tree 2 additionally showed a positive genetic structure in Adults II with a coancestry value of 0.42, which was considerably higher than those values expected for full sibs (0.25). These differences may be the result of temporal variation in the mating, dispersal patterns of the species through time, or a result of changes in plant density within the tree through time. As a perennial, L. speciosa exists as multiple generations within a population at any particular time. In fact, the oldest individual sampled was 33 years old, and the youngest was 1-year-old, and some individuals can live up to 45 years (Hernández 1992).
An absence of a fine-scale genetic structure in seedlings for both trees, and its presence as we move up in age classes was evident. Other studies have also noted an increase in genetic structure between earlier stages and later ones. Kittelson & Maron (2001) found an increase in genetic structure in Lupinus arboreus Sims between seeds and juveniles attributed to selection associated with adaptation to differing fine-scale environmental pressures between seed set and stand establishment. Cabin (1996) compared genetic diversity between the seed bank and juveniles in Lesquerella fendleri (A.Gray) S.Watson and found that the lack of structure in the seed bank was likely the result of the contribution from many overlapping generations. The stronger genetic structure in adults than in seedlings in the terrestrial orchid Orchis purpurea Huds. was mainly attributable to recurrent population crashes and recovery (Jacquemyn et al. 2006).
The absence of a fine-scale genetic structure in seedlings, and its presence as we move up in age classes in L. speciosa could be explained by localized selective pressures that would favor the differential survival of selected seedling genotypes to the juvenile class or the result of the establishment of several generations of siblings sharing the same maternal plant through time. Since L. speciosa is a perennial species, we have several generations in each class category, except for the Seedlings class, in which all individuals are the same age. This observation indicates that the lack of structure is probably due to the fact that the seeds are derived from different maternal plants. The number of reproductive individuals in a particular year is relatively low, as Hernández (1992) reported that only about 6 % of the total number of individuals were actually reproducing during the years of that study (1987 and 1989). We found a higher proportion of individuals from Adult I and Adult II categories that showed evidence of reproduction in the current and past year. This information was obtained from direct observations of flowers from the current year or capsules from the previous year, suggesting that over those two years around 21 % of individuals in these age classes had reproduced. It is likely however that the effective number of individuals contributing seeds to the population is probably even lower than 21 % of older plants, due to the fact that fruit set is low with usually less than 15 % of flowers actually going on to produce seeds (Medina 2004). It appears that the few individuals reproducing in a particular year serve as the maternal plants for seedlings scattered randomly around the canopy of Q. deserticola.
Seedlings do not show high mortality rates and there is a 71 % probability of the seedlings to survive to the juvenile stage probably due to the fact that seedlings are protected from desiccation due to the high density of lichens on the branches (Hernández 1992). Since we have low mortality rates as a population grows and more cohorts are present in the same age class, a fine-scale genetic structure would be found due to an increase in the overlap of seed shadows (of the same maternal plants over many generations), although the possibility of selective survival of some genotypes cannot be totally excluded.
Process affecting genetic structure. The fine-scale variability and differentiation of age classes above the seedling stage in these single-tree populations of L. speciosa suggests relatively small, clumped genetic groups. The fact that the fine-scale structure is only significant at distances up to 25 cm, which is generally less than the distance separating branches in the trees, suggests that the structure is wholly found in the horizontal plane. This could be explained by various mechanisms, including clonal growth, selfing, selection, and localized seed dispersal.
Clonal growth could contribute to this pattern and the indication of a full-sib relationship within the Adults II size class in Tree 2 suggests a pattern of clonal propagation (Cruse-Sanders & Hamrick 2004). However, our observations refute this possibility. Due to the production of one pseudobulb per year, an increase in size of those pseudobulbs as a plant ages, and the persistent connection among pseudobulbs in the field, we could identify and separate different individuals in about 90 % of the cases (Table 2). In cases when a cluster of pseudobulbs presented more than one front of growth, there was an overall 75 % possibility (79 % in Tree 1 and 74 % in Tree 2) that in fact each front corresponded to a genetically distinct individual. This finding suggests that multiple fronts are mostly, but not uniquely, the result of multiple establishment events instead of distortions of the apical meristem resulting in clonal growth.
Selfing is another potential process that could be affecting the fine-scale genetic structure. When all individuals in the population were considered in the analysis, the fixation values were not significant for any tree (F = 0.188 and F = 0.169), indicating an over-all lack of inbreeding. When examined by age class, F varied and indicated that individuals in the oldest age class category (Adults II) were not randomly mating (F = 0.36 and F = 0.275 for Tree 1 and 2 respectively). Our direct inference of selfing rate (Table 4) further confirmed selfing in the in the oldest size class (at 30 %) in Tree 1 but did not indicate selfing in the same size class in Tree 2. It also suggested that selfing was occurring at low rates in other size classes as well.
Pollinator visitation is required for pollen movement in the species, as observed by the absence of fruit set in pollinator exclusion experiments (Ávila-Díaz 2007). Manual pollinations indicate that there is much larger production of fruits as a result of cross-pollination than self-pollination, which is supported by low levels of self-compatibility found in the species (SCI = 0.18) (Ávila-Díaz 2007). These experimental results indicate that selfing is not common, however our results show that selfing is possible and likely to be occurring at a low level in these single-tree populations of L. speciosa.
Chung et al. (2003a) noted that variation in F values among age classes could be due to temporal variation in selfing versus outcrossing rates, since selfing contributes to modify the fixation index. In L. speciosa it appears that occasional selfing may partially contribute to the fine scale genetic structure. Its contribution is limited and the factors influencing that selfing cannot be inferred from this study.
Localized seed dispersal patterns could be contributing to the fine-scale genetic structure and this spatial pattern with establishment close to maternal plants as observed in other species (Kalisz et al. 2001, Trapnell et al. 2004). Seed production in orchids is generally very high, and in L. speciosa is estimated at ca. 600,000 seeds per fruit (Medina 2004). Dispersal of the small anemophilous seeds can simultaneously show patterns of both long-range dispersal (Arditti & Ghani 2000, Tremblay et al. 2005) and the development of fine-scale genetic structure, due to the establishment of seeds close to the parental plant (Peakall & Beattie 1996, Chung et al. 1998, 2004, Machon et al. 2003, Trapnell et al. 2004, Jacquemyn et al. 2006, Chung & Chung 2007).
It has been suggested that orchid seeds would benefit from establishing in preexisting clusters of plants, since they provide increased humidity, nutrients that would favor their germination and establishment, as well as ensure the presence of the mycorrhizal fungi necessary for their growth (Dressler 1981, Arditti et al. 1990, Trapnell et a1. 2004). Ávila-Díaz (2007) and Ávila-Díaz et al. (2013) found that many fungal species are carried within the tissue of L. speciosa, and that some mycorrhizal fungi are likely inherited from the parental plant through the placental tissue; therefore, seeds carry the symbiotic fungi with them. This finding suggests that there is no limitation on the establishment of seeds to locations with pre-existing fungi (i.e. L. speciosa plants). However, seeds would still benefit from establishment on pre-existing clusters due to increased nutrients and humidity, since of all the individuals sampled, about 10 % were part of a cluster.
The pattern of fine-scale genetic structure in our two single-tree populations suggests a combination of localized seed dispersal and establishment, coupled with limited selfing, with the structuring becoming apparent in juveniles maybe because selection of adaptive traits in surviving individuals. However, this clustered dispersal is found is relatively limited with the fine-scale genetic structure to only 25 cm, suggesting that some long-range seed dispersal is occurring across the metapopulation (Chung et al. 2003b).
Gene flow via pollination may also be contributing to this pattern. Non-rewarding species such as L. speciosa generally favor pollinator movement among populations, therefore reducing fine-scale genetic structure (Peakall & Beattie 1996, Tremblay et al. 2005, Jacquemyn et al. 2006, Pfeifer & Jetschke 2006). Bumble bees, principally Bombus pensylvanicus sonorous and B. ephippiatus are the primary pollinators of L. speciosa (Ávila-Díaz & Oyama 2007) and the lack of reward offered by the plant would suggest an increased movement of these pollinators and their carried pollen among populations, serving to reduce the fine-scale genetic structure.
Conservation implications. Fine-scale genetic studies can be of great importance for establishing conservation strategies, since they do not only detect the presence of genetic variation within a population, but also show how this variation is distributed among individuals (Escudero et al. 2003). Such information has been important for developing sampling strategies for ex situ conservation, by determining specific minimum distances for collection of individuals for the maintenance of genetic diversity. Jin et al. (2003) has shown that collection of Glycine soja Sieb. et Zucc should be performed at 10 m intervals to replicate patterns of population diversity, while Tero et al. (2005) showed that collection of Silene tatarica (L.) Pers. less than 7.8 m apart should be avoided to prevent low levels of genetic diversity in collected explants.
Our work supports the findings of earlier studies of L. speciosa which have indicated high levels of genetic diversity at range-wide as well as regional scales (Ávila-Díaz & Oyama 2007, Rojas-Méndez et al. 2017); however, our study extends this pattern to the individual single-tree population level and shows that individual trees maintain very high levels of diversity as well. The presence of this level of genetic diversity and fine-scale structure indicates that even in light of the recent reduction of population sizes through direct plant removal and habitat loss, L. speciosa has the potential to regenerate genetically diverse populations from few remaining intact trees. The long-lived nature of the species ensures that single-tree populations include past genetic diversity of now reduced metapopulations, a fact possibly contributing to the future reestablishment of exploited populations from few remaining trees if further reductions of habitat take place.
Due to the complete elimination of some populations from the range of distribution of the species there is current interest in using newly-developed methods of tissue culture (Sarabia-Ochoa et al. 2010) together with wild-collected samples to reestablish populations. Our work with L. speciosa shows that intact single-tree populations serve to maintain a large subset of the diversity found across the larger metapopulation. Sampling for potential ex situ conservation or for in vitro propagation for later restoration could acquire a large level of diversity from remaining intact single trees. The genetic diversity of the remaining individuals could be propagated and reintroduced to the environment at a level of genetic diversity closely resembling levels of the pre-disturbed population. Due to the known regional genetic variation and presence of rare alleles which could have an adaptive or evolutionary significance, reintroduction using in vitro propagated plants should utilize tissue collected from geographically close populations (Ávila-Díaz & Oyama 2007, Diniz-Filho et al. 2012).
Future studies. While our work has served to illustrate the pattern of genetic diversity and fine-scale genetic structuring in single-tree populations occurring within a well-preserved metapopulation, more work is needed to fully understand the genetic structure and drivers of that genetic structure in L. speciosa to further its conservation. Specific outstanding questions are, i) how is single-tree genetic diversity maintained within a perturbed forest and how long does an individual host tree maintain a significant level of diversity; ii) what is the level and influence of selfing on the population genetic structure of L. speciosa; and iii) what is the pattern of geographical substructuring across the full range of L. speciosa and how can we better understand the limits of regional variation to establish conservation units defined by genetic structure.











 nueva página del texto (beta)
nueva página del texto (beta)



