1. INTRODUCTION
Concrete electrical resistivity was measured comparatively early with respect to the application of other electrochemical techniques in concrete because studies are reported from the 40-50’s (Hammond and Robson, 1955; Monfore, 1968) related to the characterization of concrete as an electrical insulator to be used in train sleepers and because it was applied to non-destructive measurement of cement setting (Calleja, 1953). It is in the decade of the 60’s when reinforcement corrosion was started to appear as an important potential distress and electrochemical techniques started to be applied, in particular polarization curves (Gjorv et. al 1986; Gouda and Monfore 1965).
However, its role in these electrochemical experiments was not appraised until Polarization Resistance technique, Rp, was used to measure the instantaneous corrosion rate (Andrade and Gónzalez 1978; González et.al 1980), because their values could be very much affected by the ohmic drop if not removing resistive component from the recorded value. The systematic measurement of the ohmic drop affecting Rp measurements enabled the evidence that the concrete resistivity is a direct function of concrete porosity and its degree of water saturation (Andrade et. al 2000a; McCarter and Garvin 1989) and then, the corrosion rate results a direct function of resistivity with the consequence that ohmic control is the key rate controlling mechanism of reinforcement corrosion.
It is in the decade of the 90’s when the interest on resistivity arises again when the relation between chloride diffusion and concrete resistivity is demonstrated (Andrade et al, 2000b). To explore this relation was not appreciated and instead, most of the researchers focused to develop models and tests on chloride migration (Andrade, 1993; Tang, 1996). However, the author of this communication has been attracted by the potential numerous applications of concrete resistivity and in particular has identified that it is the key parameter linking microstructure with transport ability of concrete and has studied in depth the fundamentals of resistivity in particular the possibility to predict the reinforcement service life from its characterization (Andrade et al, 1993; Andrade, 2004). In present work some of the microstructural bases of the resistivity as universal parameter controlling transport processes in concrete as porous medium are described as well as the relation between reinforcement corrosion and degree of saturation which makes to vary concrete resistivity.
2. CONCRETE RESISTIVITY FUNDAMENTALS
Concrete electrical resistance, R, is the relation between the voltage drop, V, applied to a conductive body and the current, I, induced by it.
This Resistance, if standardized to a regular geometry, enables to know the resistivity through Ohm’s law which is given in equation 1 (d= the distance between electrodes and A is the cross-section area in figure 1).
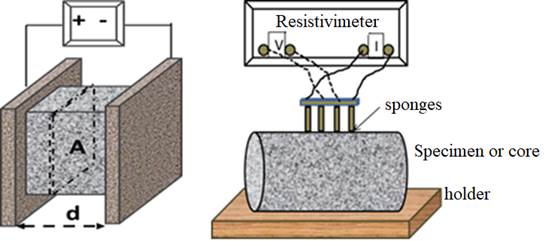
Figure 1 Left: direct, method to measure resistivity (the pore network is made evident for the sake of the representation). Right: four points or Wenner method. Concrete resistivity is an indication of the concrete porosity and degree of water saturation.
The most common method of measurement of resistivity is the “direct” or “bulk” method (figure 1-left). Two electrodes as placed in two parallel faces of a concrete specimen or disc and voltage is applied. The other common method is that known as “four points or Wenner method” shown right in the same figure.
2.1 Evolution of resistivity during setting and hardening
When water is mixed with the cement powder the paste formed is very fluid and then the resistivity is very low (figure 2), however as soon as the paste is setting, the resistivity increases following cement hydration (Calleja, 1953). The increase continues during hardening as porosity evolves with cement hydration. This increase with time serves to monitor the “aging factor of hydration” which will be addressed later.
2.2 Relation resistivity and mechanical strength
The increase of resistivity with time is parallel to that of mechanical strength due both parameters depend on concrete porosity. In figure 3 is shown their relation for numerous concretes which indicates that the resistivity may be used to predict mechanical strength when the specimens are of the same cement type and cured in standardized conditions.
2.3 Relation of Resistivity with pore microstructure and water saturation
Concrete is a porous body in which the solid phases are non-conductive being the pores filled with a solution which is the conductive phase. Then the resistivity/conductivity of the concrete will depend on the total pore volume and on its pore size distribution. As higher is the porosity, lower is the resistivity providing the concrete is water saturated. If the concrete is not saturated then, the resistivity is an indication of concrete degree of saturation (McCarter and Garvin, 1989; Andrade et. al, 2000b). This relation can be expressed through a modification of Archie’s law (Archie, 1942), where (0= the resistivity of the pore solution (average value from 10 to 50 (.cm), W is the volumetric fraction of water and ( is the tortuosity factor, (:
Regarding the influence of the chemical composition of pore solution, (0, its impact in the total resistivity following equation 2 is small providing the concrete remains alkaline. If concrete is carbonated then, the value of (0 is much higher.
An illustration of this empirical relation is given in figure 4 (Andrade, Bolzoni, Fullea, 2011) where four concrete mixes have been conditioned to several relative humidities in which the resistivity was measured together with the weight. It indicates that below a RH of 65% the resistivity rises exponentially while it is above 85-90% RH when it reaches the minimum values due to the capillary pores that are starting to be filled with evaporable water.
Figure 4 Relation between volumetric fractions of porosity saturated with water and resistivity of four different mixes. The value of ( of equation 2 is 2.52 in the figure (Andrade, Bolzoni, Fullea, 2011)
2.4 Influence of temperature in the Resistivity
With respect to the influence of temperature, it has an important effect on resistivity: resistivity increases when temperature decreases. This effect only can be generalized if the ( values are standardized to a reference temperature that it is proposed to be 25ºC. Other possibility is the use of Arrhenius law; however, it has been detected that the Activation energy depends on the degree of saturation and a single value seems not exiting (Andrade, Zuloaga, et. al, 2011). For practical applications, however the effect can be neglected if the temperature is varying from 18 to 22ºC. Larger variations may need standardization.
On the other hand, an increase in temperature usually means evaporation of pore water, which in turn means increase of resistivity. That is, the final effect of temperature in the corrosion is counter-influencing as an increase in temperature may produce a slowing of the Diffusion coefficient and the corrosion rate due to the drying. Therefore, the incorporation of temperature effects on models is very premature and more results are needed.
3. RELATION BETWEEN RESISTIVITY, DIFFUSIVITY AND CORROSION RATE
3.1 Resistivity-Diffusivity
Being concrete a porous material, Resistivity is related to its ionic transport ability by applying Einstein law on conductivity-diffusivity which relates the movement of electrical charges to the conductivity of the medium (Andrade, 1993) as represented in figure 5 in a log-log graph:
Where:
De |
= effective diffusion coefficient |
F |
= a factor, which depends on the external ionic concentration |
(ef |
= “effective” resistivity (in this case of concrete saturated with water) |
( |
= conductivity (inverse of resistivity) |
A value of kCl of 20x10-5 can be used for external chloride concentrations of 0.5 to 1 M.
3.2 Resistivity- Corrosion Rate
It is the dependence with moisture of the resistivity which explains the relation between it and the reinforcement corrosion rate which is illustrated with the graph Icorr-resistivity (Andrade et. al. 2000a; Lambert et. al., 1991) of figure 6, in which it is illustrated the average relation and some values of a particular test. The inclined line in the figure 6 represents the expression:
If the Icorr is given as Vvorr in mm/year this expression 3 results in expression 4:
Where Vcorr = (mm/year), 0.0116 = conversion factor between Vcorr and Icorr and ( = concrete resistivity (ohm(cm).
This relation has opened the door to derive the corrosion rate from resistivity providing the corrosion is in active state, because when the steel is passive the resistivity cannot be used to forecast corrosion rates.
3.3 Diffusion Coefficient-Corrosion Rate
It is apparent that equation 3 and equation 4 are very similar in spite that one (that of the diffusivity) is based in the well based theory of movement of electrical charges and the other (that of the Icorr) is empirical and developed for concrete (perhaps it could be applied to some porous materials as corrosion of metals in soils). What is the physical meaning of that similarity?. The explanation found with respect to the equation of the Icorr-( was the well-known “resistance control” of the corrosion activity of the micro- and macro-galvanic cells. That is, the resistivity of the electrolyte controls the maximum rate of corrosion (either the movement of the produced iron ions and that of the hydroxides produced in the cathode) while in solution the corrosion activity rate is more controlled by the energy of activation (activation control) or the concentration of the ions oxidized in the anodic areas or reduced in the cathodic ones (concentration control). This resistance control is what expresses the equation 4 of the diffusivity: the ions cannot move faster that the resistivity of the solution allows. Being the movement of electrical charges (ions) involved in the corrosion and in the diffusion, both are controlled by the resistivity of the electrolyte.
Apart from the physical meaning, it has also to be considered the mathematical similarity. This is very interesting from a practical point of view because, in addition to make possible the calculation of the diffusion coefficient and the corrosion rate from the resistivity of the concrete, it also enables the calculation of the maximum corrosion rate to be produced in a concrete if the coefficient of diffusion is known and vice versa, the deduction of the coefficient of diffusion from a measurement of maximum corrosion rate.
Operating mathematically by equalizing both expression 3 and 4 and assuming that for the sake of simplification in equation 4 the value of k= 2.6∙10-5 instead of k= 2.3∙10-5, it can be deduced that:
which aims into:
And
Table 1 gives some calculations for different values of Icorr and Def.
Table 1 Equivalence between Def and Icorr for the value of k=2.6E-5
| Def (cm2/s) | 0.1E-8 | 1E-8 | 10E-8 |
| Icorr ((m/year) | 0.1 | 1 | 10 |
It must be stressed that such relations are based in the so called “effective diffusion coefficient”, De which is a steady-state value and not in the Apparent Dap that averages the evolution of the coefficient along the testing time and it is the result of a non-steady-state regime.
3.4 Relation between resistivity and water saturation
Following with analogies, it is possible to calculate the corrosion rate from the water saturation, as this one depends on the resistivity. Substituting equation 2 and 3 in 4 results in equation 6:
Being: W= Sw∙(, Sw = concrete water saturation degree, % and (= porosity in volume, % This equation enables to deduce the maximum velocity of corrosion in a concrete in function of its volumetric fraction of pores saturated with water. Thus, as an example, for a W = 0.05 (50% of saturation degree in a concrete with 10% of porosity in volume), the maximum corrosion rate would be of 15 (m/year.
Then, in figure 7, all the concordances and analogies are summarized.
4. SERVICE LIFE MODEL BASED IN THE RESISTIVITY MEASUREMENTS
Two main aspects must be taken into account when trying to calculate the service life from the resistivity (Andrade, 2004).
It is necessary to introduce the relation of ( with time
The ( is proportional to the effective diffusion coefficient, that is the reaction of chlorides with the hydrated cement phases has to be incorporated.
4.1 Relation with time
The resistivity can be introduced in a “square root law” enabling the relation between time and the resistivity. Thus, if using the standard square root law:
Where x= depth of carbonation or chloride threshold penetration and t= time life. The model based in the resistivity was proposed (Calleja, 1953) by substituting the value of D by expression 7 which gives:
Based in this relation, a complete model has been developed (Calleja, 1953). For the sake of summarizing it is presented in equation 12 and equation 13:
Where:
ti |
= initiation period |
tp |
= propagation period |
(ef |
= effective resistivity (at 28 days of wet curing) |
kCO2, Cl |
= environmental factor depending on exposure class |
Knowing the value of the resistivity in the same specimen than that used for mechanical strength at 28 days, this model enables the calculation of the time to corrosion and the corrosion propagation period, if some information on the reaction ability of the cement phases and the aging factor are known.
4.2 Consideration of chloride reaction and other factors
As has been mentioned, the ability of resistivity to quantify diffusivity is based in one of the Einstein laws which relates the movement of electrical charges to the conductivity of the medium (Andrade, 1993; Andrade et al, 1993; Andrade, 2004; Garboczi, 1990) (see equation 3). This expression only accounts for the transport of the chloride ions through the pore network which is insufficient to characterize the transport through concrete where reaction of chlorides takes place and this reaction and the hydration make to evolve the porosity. Then some factors have to be applied to equation 3 to account for these effects together with the value of the k factor which takes into account the concentration of the chloride or aggressive substance.
The factors introduced in the equation 3 have been:
k has been named “environmental factor”. It depends on chloride concentration and in the case of carbonation, on the concrete moisture content (Andrade, 1993; Andrade, 2004)
r b “retarder or reaction factor” (Andrade et al, 2014) which multiplies the resistivity to account for the “retarder” effect of chloride binding during penetration of chlorides. It can also be applied to the case of carbonation. This is due to carbonation progresses when the concrete is partially saturated. That is, as higher is the porosity or the empty pores due to dry conditions, higher the carbonation depth will be but a certain moisture level is necessary for the carbonation reaction to proceed.
Finally, the “aging factor” q (Andrade, Castellote, D’Andrea, 2011) which accounts for the evolution with time of the porous microstructure.
These factors have been quantified to introduce them in an expression linking resistivity with time that will be described later.
Environmental factor F
The environmental factors FCl and FCO2 depend on the exposure conditions (Andrade, 1993; Andrade, 2004). Table 2 presents values that were calculated by inverse analysis of test results obtained on real structures.
Table 2 Values of environmental factors, kCl and kCO2, following the exposure classification of EN206
| Exposure class | F (cm3Ω/year) |
|---|---|
| X0,XC1,XC2 | 200 |
| XC3 moderate humidity | 1000 |
| XC4 cycles wet and dry | 3000 |
| XS1 (d > 500 m distance to the coast line) | 5000 |
| XS1 (d < 500 m distance to the coast line) | 10000 |
| XS2 submerged | 17000 |
| XS3 tidal | 25000 |
Reaction factor r b
The reaction factors rCl and rCO2 (Andrade et al, 2014) depend on the type and amount of cement and therefore on the reaction of the penetrating substance with the cement phases. Equation 3 can be expressed as:
The values can be calculated either by direct measurement, or indirectly by measuring the relation between the effective and apparent diffusion coefficients, or by calculation based on the cement composition. Table 3 presents examples of rCl values that were calculated based on test results obtained by comparing steady and non-steady diffusion coefficients.
Aging Factor q
It accounts for the refinement of the concrete pore system results in an increase of resistivity with time (Andrade, Castellote, D’Andrea, 2011). The resistivity evolves with time due to the progression of hydration, the combination of the cement phases with the chlorides or carbon dioxide which usually decreases the porosity and by the concrete drying out (depending on the environment. It can be calculated through the expression 15.
Where:
Values of q found for different cement types are given in table 4.
Table 4 Values of the ageing factor
| Cement | q | Standard Deviation |
|---|---|---|
| I | 0.22 | 0.01 |
| II/A -P | 0.37 | 0.06 |
| II/A-V | 0.57 | 0.08 |
The relation between q and the aging factor n of the diffusion coefficient gives the expression 23:
4.3 Propagation period
In the case of considering the propagation of corrosion (tp), considering the loss in rebar diameter, or pit depth, (Pcorr) as the limit corrosion attack, the service life of structure can be written by the expression 9:
The relation for the service life prediction can be then formulated as follows (16):
Where:
Pcorr |
= steel cross section reached at the time tp |
(ef |
= resistivity at 28 days in saturated conditions |
q |
= aging factor of the resistivity (table 4) |
( |
= environmental factor of the corrosion rate (it can be of 10(2 for carbonation and 30(5 for chlorides) |
Kcorr |
= constant with a value of 26 µA/cm2·k(·cm= to 26 mV/cm relating the resistivity and the corrosion rate Icorr |
Complete expression of the service life model based in the resistivity.
Then, the final expression of the service life model based on resistivity is:
Example of application
For the initiation period the application of the above theory can be shown by way of example, assuming a concrete with a cover depth of 4 cm made with cement type I with silica fume (reaction factor = 1.5 and aging factor = 0,22) to be placed in exposure class XS3 (tidal and splash conditions). Considering a service life of 100 years, the values of the reaction, as well as the environmental and aging factors are presented in Table 5. The calculations indicate that the resistivity needed at 28 days of age, measured in saturated conditions, is 215 (-m.
Table 5 Input data for a calculation of the concrete resistivity
| Cement type I with silica fume | rCl = 1,85 |
| Exposure class (XS3) | F (cm3Ω/year) = 25000 |
| Service life | t (years) = 100 |
| Cover depth | XCl (cm) = 4 |
| Ageing factor during 10 years | q = 0.22 |
With this resistivity the length of the propagation period following Table 6 is:
Table 6 Input data for the propagation period
| Limit Diameter loss, Pcorr | 100 (m = 0.01 cm |
| pef at 28 days | 21.5 Kohm.cm |
| q applied during 100 years | 0.22 |
| Ws in saturated conditions | 1 |
This propagation period may be included in the 100 years or considered apart as an additional safe time until cracking is produced.
5. PRODUCTION OF CONCRETE FOR A SPECIFIED APPARENT RESISTIVITY
Once known the resistivity which is needed to reach a nominal service life, it remains to describe how the concrete producer can design a mix to fulfil the service life specification. This can be done (Andrade and D’Andrade, 2010) by considering a modification of Archie’s law linking resistivity and porosity:
where (28d is the resistivity of concrete under saturated condition at 28 days, ( is the tortuosity coefficient which is estimated by fit to the experimental data, and ( is the total porosity.
The coefficient ( depends on the concrete composition which is identified to the tortuosity, and could be determined from type or family of cement type by means of measuring the porosity and the resistivity. The values found in present research are. For type I cement (= 1.9, for type II-AV (= 2.3 and for type II AP (= 1.6.
From the specified resistivity the paste porosity can be obtained and through Power’s relation on porosity and w/c ratio
To use (p in the model based on Archie's law, it must convert the porosity of the paste ((p) to porosity of the concrete ((). For this, it is applied a simple method based on multiplying the percentage of capillary porosity of the paste by the volume of paste (() in the concrete.
It is feasible to prepare a mix with the needed effective resistivity at 28 days, providing the consideration of the type of cement and its retarder factor. The concrete producer should verify by testing the reaching of the specified resistivity while the cement producer should give the retarder factor of his cements.
So, the following concrete design methodology based on Archie’s law model is proposed to achieve the prescribed value (28d:
Select a type of cement. It fixes the values of reaction factor (r) and tortuosity (() are defined.
Select a w/c ratio and calculate porosity of the paste following Powers’ model
Then calculate the expected resistivity through
6. FINAL COMMENTS
Concrete is a very complex material but which is placed on site in many manners by relatively simple practices. It needs to be modelled by sophisticated models, but also by simple ones which could help to improve the quality and spread the tools for it. The electrical resistivity, being a non-destructive method simplifies very much the control of the durability. On the other hand, it enables multiple applications in concrete technology and the quantification of the expected life. It has been summarized some of the possible applications of the concrete electrical resistivity values. Its main advantage is that the measurement is non-destructive and the concrete can be monitored. Concrete resistivity is able to inform on:
- Porosity
- Degree of water saturation
- Degree of curing
- Cement setting time
- Concrete mechanical strength
- Reinforcement corrosion rate
- Gas and water permeability
In present paper is shown the fundamental relations of resistivity with diffusivity and with the reinforcement corrosion rate. Resistivity is the parameter enabling to link microstructure with the macro-performance Also has been summarized the model for service life prediction based in Einstein law relating electrical resistance or conductance with the diffusion coefficient. Making certain assumptions this basic law can be applied to the advance of carbonation front or chloride threshold, and to the representation of steel corrosion propagation. This model can be used for calculating cover thicknesses from actual resistivity values or the minimum resistivity for a certain cover thickness.











 nueva página del texto (beta)
nueva página del texto (beta)








