INTRODUCTION
We have witnessed considerable advances in the estimation of regional and interregional extensions of input-output models since the pioneering incursions of Isard (1951) and Leontief et al. (1953). Despite those efforts, the scarcity of information associated with the high cost of obtaining interregional trade flows based on survey data remains as one of the main obstacles to the estimation of interregional input-output systems. This has made the so-called non-survey estimation methods of interregional systems gain popularity among academic researchers and practitioners (Round, 1983).
Round (1983) recalls that the use of the terms survey and non-survey methods suggests the existence of two exclusive and well-defined research techniques. However, interregional input-output systems are often constructed under hybrid approaches, combining various techniques according to the quantity and quality of primary data available. This paper describes the process of estimation of the interregional input-output systems for Mexico, for the year 2013, using the method known as Interregional Input-Output Adjustment System (IIOAS), based on Haddad et al. (2016a). The system is estimated under the very same methodological procedure and consider the 32 regions in Mexico whose economies are disaggregated in 37 sectors. There are recent efforts to estimate regional and interregional input-output systems for Mexico (e.g. Dávila, 2015; Assuad and Sánchez, 2016; Chiquiar et al., 2017).3 However, to the best of our knowledge, this is the first interregional system that takes into account explicitly the economies of the 32 Mexican states.
The IIOAS is a hybrid method that combines data made available by official agencies, such as the Instituto Nacional de Estadística y Geografía (INEGI), with non-survey techniques for the estimation of unavailable information. The main advantages of the IIOAS are its consistency with information from the National Accounts Statistics and the flexibility of its regionalization process, which can be applied to any country that: (i) publishes standard make and use tables; and (ii) provides a regional information system at the sectorial level. Such flexibility can be attested by recent applications for distinct interregional systems: interisland model for the Azores (Haddad et al., 2015), interregional models for Colombia (Haddad et al., 2016a), Egypt (Haddad et al., 2016b), Greece (Haddad et al., 2018), Lebanon (Haddad, 2014), Morocco (Haddad et al., 2017a), and Brazil (Haddad et al., 2017b).
The estimated systems are expected to be able to capture the existing specificities in the productive structure of each Mexican region and, in addition, contribute to the methodological debate on the estimation of interregional input- output systems under conditions of limited information (Hulu and Hewings, 1993; Riddington, Gibson and Anderson, 2006; Zhang, Shi and Zhao, 2015; Tobben and Kronenberg, 2015; Flegg et al., 2016). It also adds to a broader literature that deals with a large range of methods, extending from the earlier work of Jan Oosterhaven (1981), to Roy and Thill (2004) and the contributions of the entropy modelers starting with Alan Wilson (1970) and continuing with the cross entropy approaches of Esteban Fernandez-Vazquez et al. (2015).4
The paper is organized as follows: section 1 describes in detail the methodological procedure used in the construction of the interregional system for Mexico based on the IIOAS method. Section 2 presents the regionalization procedure. Section 3 presents an illustrative analysis using different indicators from the estimated databases, revealing some main structural features of the economy of Mexico. Final remarks follow.
I. INTERREGIONAL INPUT-OUTPUT MATRIX FOR MEXICO
Initial Data Treatment
The estimation of the Interregional Input-Output Matrix for Mexico (IIOM-MX) is based on the Interregional Input-Output Adjustment System (IIOAS) method. The IIOAS method was developed to estimate interregional input-output systems under conditions of limited information. In the case of Mexico, we have used data from national and regional accounts provided by the Instituto Nacional de Estadística y Geografía (INEGI) for the years 2013 and 2014. The data consist mainly of the Supply and Use Tables (SUT) at the national level, and regional data on sectoral GRP and macro regional aggregates.
The first step in data treatment was to build the national input-output matrix for Mexico from the SUT. We have organized the information available at INEGI,5 according to figures 1 and 2. The structure of the Make Table (o_pc_2) was then used to transform the new Use Table from a commodity by sector into a sector by sector system of information. The auxiliary matrix generated by the structure of the Make Table is often called the market share matrix. Finally, the national structure of 80 sectors was aggregated into 37 sectors to match the auxiliary data available at the regional level.
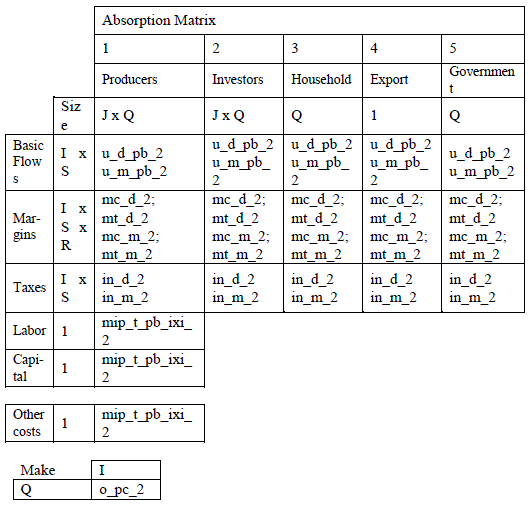
Note: J sectors; Q regions; I roducts; S sources (domestic and imort); R margins.
Source: Instituto Nacional de Estadística y Geografía (INEGI) Cuadros de Oferta y Utilización: u_d_b_2: Utilización de bienes y servicios a recios básicos | Economía total / Origen doméstico | Subsector SCIAN u_m_b_2: Utilización de bienes y servicios a recios básicos | Economía total / Origen imortado | Subsector SCIAN mc_d_2: Márgenes de comercio | Economía total / Origen doméstico | Subsector SCIAN mt_d_2: Márgenes de transorte | Economía total / Origen doméstico | Subsector SCIAN mc_m_2: Márgenes de comercio | Economía total / Origen imortado | Subsector SCIAN mt_m_2: Márgenes de transorte | Economía total / Origen imortado | Subsector SCIAN in_d_2: Imuestos netos de subsidios | Economía total / Origen doméstico | Subsector SCIAN in_m_2: Imuestos netos de subsidios | Economía total / Origen imortado | Subsector SCIAN o_c_2: Oferta de bienes y servicios a recios básicos | Economía total | Subsector SCIAN Matriz de Insumo Producto: mi_t_b_ixi_2: Matriz simétrica de insumo roducto. Industria or industria | Economía total / Origen doméstico e imortado | Subsector SCIAN
Figure 1 Schematic Structure of the IIOM-MX
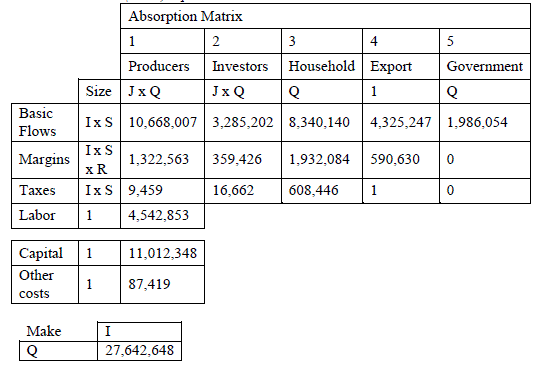
Note: J sectors; Q regions; I roducts; S sources (domestic and imort); R margins.
Figure 2 Schematic Structure of the IIOM-MX
The next step was to disaggregate the national data into the 32 regions of Mexico. The details of such procedure are described in the next two subsections.
Estimation of the Interregional Trade Matrices
In order to estimate the interregional system, it has been necessary to estimate the trade matrices among the 32 regions of Mexico. This procedure has been made by calculating three components: (i) the regional demand for domestic products; (ii) the regional demand for imported products; and (iii) the total supply of each region to the domestic and foreign markets, by sector.
We have assumed that regional demands for domestic and import products follow the national pattern for all users. In other words, economic agents share the same technology and preferences everywhere. However, it is important to note that we have estimated different trade matrices for each sector, which has allowed us to have different regional sourcing for intermediate inputs and final products.
The regional demand for domestic products is calculated, for each user, using the information provided in the matrix of demand-generating coefficients (DOMGEN). These coefficients are defined as the ratio of each element of the national use matrix to its respective column total.
For intermediate consumption, the ratio is defined as follows:
Were
Regarding the domestic absorption components (investment, household consumption, and government expenditure), we have used the ratio of each i-element to its respective column sum:
Where
Thus, from equation (2) to (4), we may have vectors of size 37 x 1, cinvdom , and chou dom , and cgov dom, with all the investment demand, household consumtion and government exenditure ratios, respectively.
The gross regional demand for domestic products is obtained by multiplying these coefficients - equations (1) to (4) - by (i) a matrix with the total sectoral output of each region in the main diagonal and zero elsewhere, Xr ; (ii) the total investment demand of each region, invtr; (iii) the total household consumption of each region, houtr ; and (iv) the total government expenditure of each region, govtr :
where IC r, dom is a matrix of intermediate consumption of domestic products; inv r,dom is the consumption vector of capital goods produced domestically; hou r,dom is the household consumption vector of domestic products; and gov r,dom is the vector of government expenditure on domestic products; all for each region r
Therefore, the (gross) total demand for domestic products in each region is given by
Where demdom r is the total demand vector for domestic products of size 37 x 1 for each region r.
The procedure to estimate the demand for imported products is similar. Analogously, we have created a matrix of demand-generating coefficients for imported products (IMPGEN) defined to be the ratio of each element of the national matrix of imports over the respective column sum in the use matrix.
For intermediate consumption, the coefficient represents the share of imports in terms of national production as follows:
Where
Analogously to domestic ratios, from equation (10) we can have a matrix of size 37 x 37 (sector x sector), CIC imp , with all the intermediate consumption ratios related to imported inputs.
Further, the coefficients for the final demand elements are given by
Where
Therefore, the demands for imported products, by region, are defined as
where IC r, imp is a matrix with imports of intermediate inputs; inv r, imp is the imports vector of capital goods; hou r, imp is the vector of imports by household; and gov r, imp is the vector of government expenditure on imports; all for each region r.
The total demand for imported products by region is given by
In order to generate a matrix of regional demands for domestic products, we have placed all demand vectors for domestic products ( demdom r , ∀ r = 1,..., 32) side by side, which has allowed us to have a matrix of size 37 x 32 (sector x region) - DEMDOM , where each row represents the domestic demand for sector i by each region r. Similarly, we have made the same procedure with the demand vectors for imported products ( demimp r , ∀ r = 1,..., 32), which has also allowed us to have a matrix of size 37 x 32 (sector x region) - DEMIMP , where each row represents the sectoral imports by each region r.
The next step was to estimate the sectoral domestic supply ( supdom r ) in each region, which has been done by taking the difference between the sectoral total output ( xr ) and the sectoral exports ( exp r ) in each region.
supdomr = xr - expr , ∀ r = 1, ... , 32 (19)
Similarly, placing all regional vectors side by side, we have created a matrix of size 37 x 32 (sector x region) - SUPDOM , where each row represents the total regional domestic supply of sector i.
Thus, having the sectoral domestic demand and supply by region ( DEMDOM and SUPDOM ), we have to ensure the equilibrium between them, in aggregate terms. We have thus adjusted the aggregate value of (gross) total domestic demand for each sector in order to have total domestic demand equivalent to total domestic supply.
The next step has been to construct, for each sector, matrices with regional trade shares ( SHIN i ). In other words, we have created matrices for each sector that represent the regional share on the total domestic trade. Considering s origin regions and d destination regions, we have estimated 37 matrices (one for each sector) of size 32 x 32 (origin x destination).
These shares have been estimated using equations, (20) and (21), based on previous work by Dixon and Rimmer (2004). Equation (20) has been used to calculate the initial ratio of the intra-regional trade (main diagonal of the trade matrix) while equation (21) has been used to estimate the interregional trade flows.
Thus, the intra-regional trade share is given by
Where
The intra-regional trade flow is defined to be the ratio of supply to demand of sector i within the region. If supply is greater than demand, we have assumed that all demand is met internally. However, based on Haddad et al. (2016a), we have multiplied the result by a factor ( f ) which gives us the extent of tradability of a given commodity. For non-tradable sectors, usually services, we have assumed that they are typically provided by the local economy. Thus, we have used initial f values close to unity 0.9 for non-tradable and 0.5 for tradable sectors.
Otherwise, the interregional trade is given by
Where
From equations (20) and (21), we generate matrices of size 32 x 32 (region x region) for each sector - SHIN i , where the intra-regional trade shares are placed on the main diagonal and the interregional trade shares off-diagonal. Note that the column values add to one.
Using the SHIN i matrices, we have estimated initial values for the trade matrices by multilying each SHIN i by its resective reference value in DEMDOM:
TRADEi= SHINi*DEMDOM*I, Ɐ i=1, … , 37 and s, d=1, …, 32 (22)
Where
This procedure ensures that the column sums of each
After the RAS procedure, we have included in each
II. REGIONALIZATION PROCEDURE
The 37 trade matrices estimated are consistent with the national supply and demand in each sector. The trade matrices, after the inclusion of the import row,
In order to deal with this issue, we have used a hypothesis proposed originally by Chenery (1956) and Moses (1955). We have applied the same regional proportion in the acquisition of inputs for all sectors and final products by all final users within a given region. In other words, we have used the same trade coefficient for all sectors or final users in the destination.
The regionalization procedure may be described by the following steps. The first step is given by the calculation of a new matrix for each sector with the trade shares, SHIN_N i. This matrix is estimated based on the ECUACION matrices as follows :
Where TRADE
*I is a matrix diagonal whose
Subsequently, we have used elements from the national use matrix to estimate the national coefficients (domestic plus imports) of intermediate consumption, investment demand, household consumption, and government expenditure.
For intermediate consumption, the matrix of coefficients is given by
CICN=ZDOM+IMP*(ICT*N)-1 (24)
Where ZDOM+IMP is the intermediate consumption matrix (domestic +imported); and ICT*N is a diagonal matrix with the values from the vector of total intermediate consumption for each sector of destination j ( ictN ) in the main diagonal. This vector, ictN , is defined as
ictN=xN-vaN (25)
Where xN is the vector with all national total sectoral output; and vaN is the vector with all national sectoral value-added.
For the final demand elements, we have taken each element of each vector over its respective total (including also indirect taxes). Thus, the investment demand, household consumption, and government expenditure coefficients are defined as follows:
Where
From equations (26) to (28), we can generate vectors with coefficients ofinvestment demand ( cinv N ), household consumption ( chou N ), and government expenditure ( cgov N ).
The next step has been to estimate the regional coefficients. In order to obtain the intermediate consumption shares, RICC , we have transformed the 37 SHIN_N matrices into 33 SHIN_S matrices of size 37 x 32, which represent, for each origin, foreign region inclusive, the consumption share of each sector in each destination region. Thus, each SHIN_S matrix represents one origin trade region, where rows show the sectors and columns the destination regions.
Therefore, using Aguascalientes (the first region) as an example, the SHIN_S for this region is composed of all the first rows of each of the 37 SHIN_N . For the second region, Baja California, the SHIN_S includes all the second rows of each of the 37 SHIN_N , and so on. Further, in order to estimate RICC, each column of each SHIN_S matrix is diagonalized and multiplied by CIC N:
Where SHIN_S* is a diagonal matrix whose non-zero elements come from the SHIN_S ; s represents the 33 origin regions, and d represents the 32 destination regions.
From equation (29), we estimated, for each origin region, 32 destination matrices of size 37 x 37 (sector x sector). These matrices contain the shares of each sector in the intermediate consumption in each destination region.
Similarly, for each of the final demand components, we estimated, for each origin region, 33 vectors of size 37 x 1, shin_s , which represents the shares of each destination region d in the acquisition of the output from each of the 37 sectors.
The final demand for capital goods (investment demand) for each region is given by
Where SHIN_S** is a diagonal matrix of the vector shin_s . For household consumption:
and for government expenditure:
In order to obtain the regional share for the indirect tax paid by each user, we have calculated some coefficients from the national tax matrix. These coefficients are calculated for intermediate consumption, investment, household consumption, and government expenditure as follows.
The matrix with the national indirect tax coefficients related to intermediate consumption ( TCIC N ) is given by
Where TICN is a matrix of size 37 x 37 (sector x sector) with the indirect taxes related to intermediate consumption in the national tax matrix; and ICTN is a diagonal matrix with the sectorial total intermediate consumption.
The vector with national indirect tax coefficients related to investment (tcinv N ) is
Where tinv N is the vector with tax related to investment, and invt N is the total demand for investment from the national use matrix.
The vector with national tax coefficients related to household consumption ( tchou N ) is given by
tchouN = thouN *(hout N )- 1 (35)
Where thou N is the vector with tax related to household consumption, and houtN is the total demand for household from the national use matrix.
Finally, the vector with national tax related to government expenditure ( tcgov N ) is
tcgovN = tgovN *(govt N )- 1 (36)
Where tgov N is the vector with tax related to government consumption, and govt N is the total demand for government from the national use matrix.
The regional coefficients are obtained by multiplying each column of SHIN_S by the national tax coefficient. Thus, the regional coefficient for indirect tax related to intermediate consumption is given by
RTCICsd = SHIN_S* * TCICN , ∀ s = 1, ... , 33; and d = 1, ... , 32 (37)
Which generates 1056 matrices of size 37 x 37 (sector x sector). These matrices represent the regional indirect tax coefficients for each pair of regions s x d (origin x destination).
For investment demand:
rtcinvsd = SHIN_S* * tcinvN , ∀ s = 1, ... , 33; and d = 1, ... , 32 (38)
which gives us 1056 vectors of size 37 x 1 that represents the proportion paid in tax related to the acquisition of products for investment in each pair of regions s x d.
Similarly, we have the regional coefficient for household consumption:
rtchousd = SHIN_S* * tchouN , ∀ s = 1, ... , 33; and d = 1, ... , 32 (39)
And for government expenditure:
rtcgovsd = SHIN_S* * tcgovN , ∀ s = 1, ... , 33; and d = 1, ... , 32 (40)
In order to have all regional coefficients in monetary flows, we have multiplied the coefficients defined above by the regional values.
Intermediate consumption:
RICsd = RICCsd * RICTd , ∀ s = 1, ... , 33; and d = 1, ... , 32 (41)
Where RIC sd is the regional intermediate consumption matrix for each pair of region (s x d), and RICT d is a matrix with the total regional intermediate consumption in the main diagonal and zero elsewhere.
Investment demand:
rinvsd = rcinvsd * rinvtd , ∀ s = 1, ... , 33; and d = 1, ... , 32 (42)
Where rinv sd is the vector of demand for regional investment for each pair of region (s x d), and rinvt d is the total regional for investment.
Household consumption:
rhousd = rchousd * rhout d , ∀ s = 1, ... , 33; and d = 1, ... , 32 (43)
Where rhou sd is the vector of regional household consumption for each pair of region (s x d), and rhoutd is the total regional household consumption.
Government expenditure:
rgovsd = rcgovsd * rgovt d , ∀ s = 1, ... , 33; and d = 1, ... , 32 (44)
Where rgov sd is the vector of regional government expenditures for each pair of regions (s x d), and rgovt d is the total regional government expenditures.
Given the estimates of sectoral foreign exports by region, ( exp r), the values are allocated directly in the relevant column of the inter-regional system. We had access to foreign exports of manufacturing sectors by region.7 For those sectors for which regionally disaggregated foreign exports were not available, we have assumed the same ratio of sectoral foreign exports to sectoral gross output to allocate foreign exports across regions.
Similar procedure has been used to transform indirect tax coefficients in monetary flows as follows:
For tax related to intermediate consumption:
RTICsd = RTCICsd * RICTd , ∀ s = 1, ... , 33; and d = 1, ... , 32 (45)
Investment:
rtinvsd = rtcinvsd * rinvt d , ∀ s = 1, ... , 33; and d = 1, ... , 32 (46)
Household consumption:
rthousd = rtchousd * rhout d , ∀ s = 1, ... , 33; and d = 1, ... , 32 (47)
And government expenditure:
rtgovsd = rtcgovsd * rgovt d , ∀ s = 1, ... , 33; and d = 1, ... , 32 (48)
In order to have the completed inter-regional system, we need the regional value-added components (VA R ). In the interregional input-output system, the total regional output (x R ) should be equivalent to the total demand of each region (DT R ). This balance checking can be done using the following identities.
Total regional output:
where X R is the vector of sectorial regional total output; RIC sd is the regional intermediate consumption matrix; RTIC sd is the indirect tax matrix related to intermediate consumption, and rva sd is the vector of regional value-added.
Total demand:
Where dt R is the total demand vector; rinv sd is the demand for investment; rhou sd is the household consumption; expr sd is the export vector; and rgov sd is the government expenditure.
Finally, an adjustment in Stocks ( stock R ) must be done to complete the interregional system:
stockR = xR - dtR (51)
III. STRUCTURAL ANALYSIS
Interregional Linkages
In this section, a brief comparative analysis of regional economic structures is carried out to illustrate some features of the system. Production linkages between sectors are considered through the analysis of the intermediate inputs portion of the interregional input-output database. Both the direct and indirect production linkage effects of the economy are captured by the adoption of different methods based on the evaluation of the Leontief inverse matrix.
The conventional input-output model is given by
𝐱 = 𝐀𝐱 + 𝐟 (52)
And
𝐱 = (𝐈 − 𝐀)−1𝐟 = Bf (53)
Where x and f are respectively the vectors of gross output and final demand; A is a matrix with the input-output coefficients a ij defined as the amount of product i required per unit of product j (in monetary terms) - i, j = 1, …, n; and B is known as the Leontief inverse.
Let us consider systems equations (52) and (53) in an interregional context, with r different regions, so that:
And
Furthermore, we may consider different components of f, which includes demands originating in the specific regions, V, and abroad, e. We obtain information of final demand from origin s in the IIOM-MX, allowing us to treat V as a matrix which provides the monetary values of final demand expenditures from the domestic regions in Mexico and from the foreign region.
Thus, we can re-write equation (55) as:
From equation (57), we can then compute the contribution of final demand from different origins on regional output. It is clear from (57) that regional output depends, among others, on demand originating in the region and on the degree of interregional integration, also on demand from outside the region.
In what follows, interdependence among sectors in different regions is considered through the analysis of the complete intermediate input portion of the interregional input-output table. The Leontief inverse matrix, based on the system (55), will be considered, and some summary interpretations of the structure of the economy derived from it will be provided. To illustrate the nature of interregional linkages in Mexico, we provide analysis of the structure of the Mexican economy derived from the Leontief inverse (multipliers) matrix, focusing on the database for 2013.
Multiplier Analysis
The column multipliers derived from B were computed (Miller and Blair, 2009). An output multiplier is defined for each sector j, in each region r, as the total value of production in all sectors and in all regions of the economy that is necessary to satisfy a euro’s worth of final demand for sector j’s output.
Further, the multiplier effect can be decomposed into intraregional (internal multiplier) and interregional (external multiplier) effects,8 the former representing the impacts on the outputs of sectors within the region where the final demand change was generated, and the latter showing the impacts on the other regions of the system (interregional spillover effects).
Table 1 shows the intraregional and interregional shares for the average total output multipliers of the 32 regions of Mexico as well as the equivalent shares for the direct and indirect effects of a unit change in final demand in each sector in each region net of the initial injection (the total output multiplier effect net of the initial change). The entries are shown in percentage terms, providing insights into the degree of dependence of each region on the other regions.
Table 1 Regional Percentage Distribution of the Average Total and Net Output Multipliers: Mexico, 2013
| Total multiper | output | Net out put | multiplier | ||
|---|---|---|---|---|---|
| Intra-regional share | Interregional share | Intraregional share | Interregional share | ||
| R1 | Aguascalientes | 0.756 | 0.244 | 0.260 | 0.740 |
| R2 | Baja California | 0.784 | 0.216 | 0.355 | 0.645 |
| R3 | Baja California Sur | 0.774 | 0.226 | 0.358 | 0.642 |
| R4 | Campeche | 0.708 | 0.292 | 0.164 | 0.836 |
| R5 | Coahuila de Zaragoza | 0.767 | 0.233 | 0.336 | 0.694 |
| R6 | Colima | 0.764 | 0.236 | 0.328 | 0.672 |
| R7 | Chiapas | 0.810 | 0.190 | 0.426 | 0.574 |
| R8 | Chihuahua | 0.766 | 0.234 | 0.302 | 0.698 |
| R9 | Ciudad de México | 0.780 | 0.220 | 0.357 | 0.643 |
| R10 | Durango | 0.775 | 0.225 | 0.353 | 0.647 |
| R11 | Guanajuato | 0.801 | 0.199 | 0.400 | 0.600 |
| R12 | Guerrero | 0.766 | 0.234 | 0.328 | 0.672 |
| R13 | Hidalgo | 0.795 | 0.205 | 0.370 | 0.630 |
| R14 | Jalisco | 0.812 | 0.188 | 0.437 | 0.563 |
| R15 | Estado de México | 0.798 | 0.202 | 0.387 | 0.613 |
| R16 | Michoacán de Ocampo | 0.784 | 0.216 | 0.377 | 0.623 |
| R17 | Morelos | 0.786 | 0.214 | 0.342 | 0.658 |
| R18 | Nayarit | 0.771 | 0.229 | 0.349 | 0.651 |
| R19 | Nuevo León | 0.813 | 0.187 | 0.446 | 0.554 |
| R20 | Oaxaca | 0.811 | 0.189 | 0.425 | 0.575 |
| R21 | Puebla | 0.784 | 0.216 | 0.359 | 0.641 |
| R22 | Querétaro | 0.793 | 0.207 | 0.376 | 0.624 |
| R23 | Quintana Roo | 0.767 | 0.233 | 0.346 | 0.654 |
| R24 | San Luis Potosí | 0.784 | 0.216 | 0.358 | 0.642 |
| R25 | Sinaloa | 0.784 | 0.216 | 0.386 | 0.614 |
| R26 | Sonora | 0.791 | 0.209 | 0.377 | 0.623 |
| R27 | Tabasco | 0.758 | 0.242 | 0.276 | 0.724 |
| R28 | Tamaulipas | 0.785 | 0.215 | 0.340 | 0.660 |
| R29 | Tlaxcala | 0.777 | 0.223 | 0.317 | 0.683 |
| R30 | Veracruz de Ignacio de la Llave | 0.799 | 0.201 | 0.406 | 0.594 |
| R31 | Yucatán | 0.790 | 0.210 | 0.402 | 0.598 |
| R32 | Zacatecas | 0.740 | 0.260 | 0.252 | 0.748 |
Source: Calculations by the authors.
Nuevo León, Jalisco, Chiapas, Oaxaca, Veracruz de Ignacio de la Llave, Yucatán and Guanajuato are the most self-sufficient regions; the average flow-on effects from a unit change in sectoral final demand are among the highest. The average net effect exceeds 40% for those regions. For some regions, such as Campeche, Zacatecas, Aguascalientes and Tabasco, the degree of regional self-sufficiency is lower, and the net intraregional flow-on effects, on the average, are below 25% of the total interregional effects.
Output Decomposition
In order to complement the multiplier analysis, the regional output decomposition is carried out in this section. We considered not only the multiplier structure but also the structure of final demand in the 32 domestic and the foreign regions.
Following equation (57), regional output (for each region) was decomposed, and the contributions of the components of final demand from different areas were calculated. The results are presented in table 2. As expected, the main contributions to the final demand of a region are given by itself, so the highest values in table are on the diagonal. In addition, the importance of Ciudad de México (R9), Nuevo León (R19) and México (R15) for the Mexican economy is verified, with the final demand originating in these regions generating the greatest contribution to the output of the other regions. The final demand for Ciudad de México (R9) contributes to 18.55% of the Mexican output, and, at the regional level, it contributes mainly to the regions México (R15), Hidalgo (R13), and Guerrero (R12). Final demand originating in Nuevo León (R19), contributes to 5.50% of total national output, and final demand originating in México (R15) contributes to 4.91% of final output. It is worth noting the importance of the rest of the world’s demand for the Mexican production, with a contribution of 27.55%.
A more systematic approach to visualize the influence of final demand from different regions is to map the column original estimates that generated table 2. The results, illustrated in figure 3, provide an attempt to reveal the spatial patterns of income dependence upon specific sources of final demand. The 32 regions are grouped in five different categories in each map, so that darker colors represent higher values.
Table 2 Components of Decomposition of Regional Output Based on the Sources of Final Demand: México, 2013 (in %)
| ORIGINAL OF DEMAND | ||||||||||||||||||||||||||||||||||
| R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | R10 | R11 | R12 | R13 | R14 | R15 | R16 | R17 | R18 | R19 | R20 | R21 | R22 | R23 | R24 | R25 | R26 | R27 | R28 | R29 | R39 | R31 | R32 | ROW | ||
| REGIONAL OUTPUT | R1 | 34.43 | 0.65 | 0.09 | 1.86 | 0.94 | 0.14 | 0.45 | 0.97 | 6.43 | 0.22 | 1.31 | 0.12 | 0.17 | 1.18 | 0.34 | 0.15 | 0.13 | 1.98 | 0.17 | 0.45 | 0.53 | 0.17 | 0.70 | 0.22 | 0.40 | 1.18 | 0.80 | 0.06 | 1.09 | 0.16 | 1.06 | 1.06 | 39.75 |
| R2 | 0.17 | 39.09 | 0.22 | 3.57 | 0.96 | 0.06 | 0.67 | 1.12 | 3.43 | 0.12 | 0.31 | 0.06 | 0.07 | 0.48 | 0.58 | 0.12 | 0.08 | 0.06 | 1.26 | 0.09 | 0.32 | 0.17 | 0.14 | 0.18 | 0.21 | 1.12 | 1.65 | 0.42 | 0.03 | 0.93 | 0.13 | 0.33 | 41.84 | |
| R3 | 0.46 | 4.78 | 39.70 | 7.88 | 2.70 | 0.08 | 1.38 | 2.39 | 9.69 | 0.38 | 0.92 | 0.10 | 0.22 | 1.04 | 1.63 | 0.22 | 0.17 | 0.09 | 3.96 | 0.16 | 0.83 | 0.50 | 0.17 | 0.50 | 0.31 | 1.81 | 3.72 | 1.23 | 0.09 | 2.13 | 0.24 | 0.65 | 9.87 | |
| R4 | 0.45 | 1.04 | 0.18 | 18.52 | 1.25 | 0.18 | 0.84 | 1.11 | 8.28 | 0.26 | 1.01 | 1.24 | 1.25 | 1.46 | 1.93 | 0.43 | 0.30 | 0.16 | 2.42 | 0.26 | 0.84 | 0.58 | 0.40 | 0.53 | 0.45 | 0.87 | 2.47 | 0.70 | 0.12 | 1.74 | 0.48 | 0.43 | 49.83 | |
| R5 | 0.23 | 0.75 | 0.11 | 1.75 | 23.40 | 0.08 | 0.40 | 1.29 | 3.54 | 0.23 | 0.45 | 0.09 | 0.09 | 0.66 | 0.71 | 0.17 | 0.11 | 0.09 | 4.26 | 0.13 | 0.30 | 0.23 | 0.17 | 0.26 | 0.27 | 0.48 | 1.01 | 0.85 | 0.04 | 0.80 | 0.15 | 0.30 | 56.59 | |
| R6 | 0.77 | 1.46 | 0.10 | 4.30 | 1.70 | 44.73 | 0.85 | 1.82 | 10.76 | 0.24 | 1.32 | 0.14 | 0.24 | 3.29 | 1.96 | 0.45 | 0.24 | 0.19 | 2.93 | 0.19 | 0.79 | 0.67 | 0.20 | 0.65 | 0.30 | 1.07 | 2.49 | 1.06 | 1.10 | 1.73 | 0.26 | 0.73 | 12.29 | |
| R7 | 0.45 | 1.80 | 0.25 | 4.03 | 1.52 | 0.16 | 40.04 | 1.69 | 11.79 | 0.32 | 1.03 | 0.30 | 0.33 | 1.40 | 2.00 | 0.41 | 0.30 | 0.16 | 3.11 | 0.37 | 1.02 | 0.67 | 0.71 | 0.49 | 0.47 | 1.13 | 4.04 | 1.08 | 0.14 | 2.17 | 0.79 | 1.28 | 15.54 | |
| R8 | 0.23 | 1.10 | 0.10 | 1.97 | 1.33 | 0.07 | 0.43 | 31.77 | 3.68 | 0.22 | 0.45 | 0.08 | 0.09 | 0.65 | 0.70 | 0.16 | 0.10 | 0.08 | 2.18 | 0.12 | 0.31 | 0.23 | 0.15 | 0.24 | 0.25 | 0.80 | 1.09 | 0.60 | 0.04 | 0.82 | 0.15 | 0.33 | 49.45 | |
| R9 | 0.56 | 1.28 | 0.14 | 1.75 | 1.34 | 0.14 | 0.56 | 1.50 | 58.06 | 0.29 | 1.54 | 0.33 | 0.84 | 1.53 | 4.97 | 0.51 | 0.58 | 0.16 | 2.06 | 0.44 | 1.48 | 1.07 | 0.22 | 0.73 | 0.33 | 0.88 | 1.58 | 1.21 | 0.26 | 2.17 | 0.29 | 0.33 | 10.86 | |
| R10 | 0.71 | 1.86 | 0.23 | 3.44 | 3.10 | 0.15 | 0.76 | 3.33 | 9.65 | 34.10 | 1.28 | 0.18 | 0.26 | 1.85 | 1.91 | 0.38 | 0.26 | 0.21 | 5.54 | 0.24 | 0.79 | 0.64 | 0.31 | 0.73 | 0.68 | 1.27 | 2.06 | 1.59 | 0.10 | 1.70 | 0.30 | 0.99 | 19.40 | |
| R11 | 0.80 | 1.04 | 0.15 | 2.12 | 1.19 | 0.18 | 0.52 | 1.32 | 10.96 | 0.27 | 35.69 | 0.20 | 0.29 | 2.11 | 1.99 | 0.60 | 0.24 | 0.17 | 2.42 | 0.22 | 0.76 | 1.10 | 0.24 | 0.82 | 0.36 | 0.71 | 1.42 | 1.08 | 0.10 | 1.41 | 0.24 | 0.58 | 28.79 | |
| R12 | 0.56 | 1.49 | 0.09 | 4.22 | 1.78 | 0.09 | 0.83 | 1.85 | 20.99 | 0.21 | 1.17 | 35.14 | 0.40 | 1.46 | 2.97 | 0.30 | 0.69 | 0.10 | 3.19 | 0.26 | 1.34 | 0.84 | 0.21 | 0.57 | 0.20 | 0.96 | 2.89 | 1.15 | 0.16 | 2.26 | 0.33 | 0.42 | 10.90 | |
| R13 | 0.45 | 1.98 | 0.14 | 2.56 | 1.03 | 0.15 | 0.67 | 1.13 | 26.85 | 0.23 | 1.17 | 0.29 | 29.01 | 1.44 | 3.34 | 0.45 | 0.41 | 0.13 | 2.03 | 0.31 | 1.66 | 0.90 | 0.28 | 0.53 | 0.33 | 0.68 | 1.84 | 0.82 | 0.25 | 2.26 | 0.31 | 0.37 | 17.01 | |
| R14 | 0.87 | 1.32 | 0.17 | 2.45 | 1.45 | 0.28 | 0.56 | 1.62 | 10.38 | 0.31 | 1.81 | 0.18 | 0.29 | 35.19 | 2.06 | 0.80 | 0.25 | 0.29 | 2.92 | 0.23 | 0.77 | 0.84 | 0.26 | 0.78 | 0.44 | 0.89 | 1.60 | 1.32 | 0.10 | 1.50 | 0.26 | 0.59 | 27.21 | |
| R15 | 0.36 | 0.80 | 0.11 | 1.53 | 0.89 | 0.12 | 0.41 | 0.94 | 28.16 | 0.18 | 1.02 | 0.26 | 0.43 | 1.20 | 32.08 | 0.41 | 0.44 | 0.11 | 1.85 | 0.26 | 0.98 | 0.85 | 0.22 | 0.44 | 0.25 | 0.54 | 1.20 | 0.79 | 0.15 | 1.46 | 0.23 | 0.23 | 21.13 | |
| R16 | 0.83 | 1.42 | 0.14 | 2.69 | 1.71 | 0.19 | 0.55 | 1.78 | 14.69 | 0.26 | 2.02 | 0.20 | 0.37 | 3.53 | 2.75 | 33.48 | 0.32 | 0.21 | 3.36 | 0.25 | 0.92 | 1.16 | 0.25 | 0.72 | 0.33 | 0.95 | 1.85 | 1.32 | 0.13 | 1.70 | 0.29 | 0.47 | 19.13 | |
| R17 | 0.30 | 0.70 | 0.09 | 2.13 | 0.80 | 0.09 | 0.52 | 0.79 | 16.84 | 0.15 | 0.71 | 0.34 | 0.29 | 0.88 | 2.44 | 0.26 | 35.79 | 0.08 | 1.49 | 0.21 | 1.11 | 0.53 | 0.17 | 0.34 | 0.20 | 0.48 | 1.47 | 0.58 | 0.13 | 1.53 | 0.19 | 0.26 | 28.10 | |
| R18 | 0.78 | 1.66 | 0.13 | 3.74 | 2.41 | 0.17 | 0.75 | 2.28 | 12.43 | 0.49 | 1.61 | 0.14 | 0.30 | 3.10 | 2.13 | 0.47 | 0.22 | 42.66 | 4.18 | 0.18 | 0.84 | 0.87 | 0.19 | 0.70 | 0.44 | 1.31 | 2.17 | 1.42 | 0.10 | 1.72 | 0.22 | 0.61 | 9.54 | |
| R19 | 0.38 | 1.15 | 0.15 | 2.59 | 3.33 | 0.12 | 0.59 | 1.84 | 5.30 | 0.32 | 0.70 | 0.14 | 0.13 | 1.00 | 0.99 | 0.26 | 0.15 | 0.11 | 38.21 | 0.18 | 0.46 | 0.35 | 0.22 | 0.45 | 0.36 | 0.75 | 1.51 | 1.93 | 0.05 | 1.22 | 0.23 | 0.54 | 34.28 | |
| R20 | 0.49 | 1.50 | 0.18 | 5.49 | 1.66 | 0.14 | 1.30 | 1.58 | 15.94 | 0.27 | 1.11 | 0.28 | 0.38 | 1.35 | 2.39 | 0.39 | 0.36 | 0.13 | 3.09 | 34.82 | 1.76 | 0.77 | 0.38 | 0.52 | 0.38 | 0.97 | 3.56 | 1.06 | 0.19 | 3.07 | 0.44 | 0.44 | 13.59 | |
| R21 | 0.32 | 0.74 | 0.12 | 2.70 | 0.78 | 0.12 | 0.78 | 0.85 | 16.40 | 0.16 | 0.90 | 0.27 | 0.48 | 1.10 | 2.41 | 0.36 | 0.46 | 0.12 | 1.70 | 0.46 | 30.69 | 0.63 | 0.29 | 0.38 | 0.24 | 0.48 | 2.13 | 0.68 | 0.39 | 3.20 | 0.30 | 0.27 | 29.06 | |
| R22 | 0.53 | 0.77 | 0.12 | 2.25 | 1.00 | 0.14 | 0.58 | 1.01 | 13.30 | 0.21 | 1.77 | 0.20 | 0.33 | 1.51 | 2.44 | 0.49 | 0.27 | 0.13 | 1.95 | 0.24 | 0.82 | 31.28 | 0.22 | 0.72 | 0.28 | 0.54 | 1.54 | 0.89 | 0.11 | 1.59 | 0.24 | 0.44 | 31.10 | |
| R23 | 0.51 | 1.87 | 0.018 | 11.15 | 2.37 | 0.07 | 0.77 | 2.60 | 12.97 | 0.41 | 1.31 | 0.12 | 0.40 | 1.00 | 2.07 | 0.24 | 0.19 | 0.07 | 4.91 | 0.24 | 0.98 | 0.80 | 35.59 | 0.61 | 0.21 | 1.34 | 3.88 | 1.85 | 0.14 | 2.16 | 1.11 | 0.23 | 7.73 | |
| R24 | 0.83 | 0.84 | 0.13 | 2.36 | 1.36 | 0.16 | 0.58 | 1.21 | 9.17 | 0.27 | 1.59 | 0.17 | 0.23 | 1.74 | 1.71 | 0.41 | 0.22 | 0.15 | 3.14 | 0.22 | 0.64 | 0.88 | 0.23 | 31.63 | 0.30 | 0.54 | 1.52 | 1.34 | 0.08 | 1.44 | 0.22 | 0.84 | 33.83 | |
| R25 | 0.58 | 3.07 | 0.27 | 4.29 | 3.08 | 0.15 | 0.81 | 3.10 | 9.90 | 0.54 | 1.12 | 0.16 | 0.25 | 2.02 | 1.75 | 0.36 | 0.23 | 0.23 | 4.91 | 0.22 | 0.77 | 0.64 | 0.30 | 0.58 | 38.54 | 2.52 | 2.43 | 1.50 | 0.10 | 1.72 | 0.32 | 0.62 | 13.10 | |
| R26 | 0.26 | 2.48 | 0.27 | 3.66 | 1.09 | 0.14 | 0.79 | 1.69 | 5.20 | 0.23 | 0.60 | 0.14 | 0.13 | 1.06 | 1.07 | 0.28 | 0.16 | 0.16 | 1.98 | 0.20 | 0.48 | 0.30 | 0.30 | 0.28 | 0.66 | 29.26 | 1.93 | 0.63 | 0.06 | 1.43 | 0.27 | 0.38 | 42.45 | |
| R27 | 0.48 | 1.64 | 0.27 | 4.85 | 1.38 | 0.21 | 1.19 | 1.53 | 10.06 | 0.37 | 1.07 | 0.35 | 0.31 | 1.58 | 2.09 | 0.51 | 0.32 | 0.18 | 2.57 | 0.33 | 1.10 | 0.63 | 0.70 | 0.56 | 0.62 | 1.18 | 26.21 | 0.83 | 0.15 | 2.21 | 0.99 | 0.40 | 33.15 | |
| R28 | 0.44 | 1.25 | 0.16 | 2.78 | 2.08 | 0.14 | 0.59 | 1.59 | 6.83 | 0.31 | 0.82 | 0.17 | 0.16 | 1.18 | 1.23 | 0.32 | 0.16 | 0.13 | 5.06 | 0.16 | 0.57 | 0.44 | 0.23 | 0.51 | 0.40 | 0.82 | 1.55 | 29.12 | 0.07 | 1.28 | 0.26 | 0.56 | 38.52 | |
| R29 | 0.37 | 0.88 | 0.12 | 2.38 | 0.90 | 0.12 | 0.68 | 1.03 | 18.46 | 0.18 | 0.98 | 0.26 | 0.59 | 1.21 | 2.63 | 0.36 | 0.41 | 0.12 | 1.95 | 0.42 | 3.18 | 0.74 | 0.29 | 0.42 | 0.25 | 0.59 | 1.95 | 0.78 | 30.69 | 2.78 | 0.33 | 0.28 | 23.65 | |
| R30 | 0.44 | 1.35 | 0.19 | 2.80 | 1.20 | 0.15 | 0.78 | 1.40 | 13.97 | 0.27 | 1.07 | 0.32 | 0.43 | 1.45 | 2.39 | 0.43 | 0.37 | 0.15 | 2.48 | 0.40 | 1.65 | 0.71 | 0.43 | 0.51 | 0.41 | 0.88 | 2.36 | 1.00 | 0.22 | 39.29 | 0.48 | 0.32 | 19.73 | |
| R31 | 0.30 | 1.31 | 0.16 | 12.47 | 1.22 | 0.09 | 1.13 | 1.30 | 7.73 | 0.19 | 0.74 | 0.17 | 0.23 | 0.98 | 1.38 | 0.25 | 0.21 | 0.10 | 2.45 | 0.29 | 0.71 | 0.45 | 1.46 | 0.36 | 0.26 | 0.73 | 5.17 | 0.99 | 0.10 | 1.83 | 44.08 | 0.24 | 10.93 | |
| R32 | 1.32 | 1.00 | 0.12 | 2.54 | 1.74 | 0.14 | 0.60 | 1.62 | 8.78 | 0.38 | 1.45 | 0.16 | 0.23 | 1.79 | 1.72 | 0.38 | 0.24 | 0.14 | 3.86 | 0.19 | 0.73 | 0.72 | 0.22 | 1.03 | 0.29 | 0.66 | 1.55 | 1.16 | 0.09 | 1.52 | 0.23 | 36.23 | 27.17 | |
| TOTAL | 0.92 | 2.49 | 0.40 | 3.35 | 2.53 | 0.37 | 0.30 | 2.54 | 18.55 | 0.65 | 2.54 | 0.62 | 0.80 | 3.63 | 4.91 | 1.08 | 0.74 | 0.38 | 5.50 | 0.78 | 2.00 | 1.41 | 0.70 | 1.23 | 1.04 | 1.88 | 2.58 | 2.06 | 0.32 | 3.58 | 0.85 | 0.71 | 27.55 | |
Source: Calculations by the authors
FINAL REMARKS
The main aim of this paper was to describe the process of estimation of an interregional input-output system for México, for the year 2013. Further understanding of the structure of the Mexican regional economies, within an integrated system, is one of the main goals of a broader collaborative project underway at the University of São Paulo Regional and Urban Economics Lab (NEREUS) the Institute for Environmental Research Xabier Gorostiaga SJ (Universidad Iberoamericana Puebla) and the Instituto Tecnológico Autónomo de México (ITAM). With this paper, we make available not only the details of the methodological procedures adopted to generate the interregional system, but also the database itself to be used by other researchers and practitioners.9
One important caveat for this work is that there are no data available for a statistical validation of the results. Results can only be validated heuristically, which is the norm in this literature. The conclusions of the paper should be taken very cautiously when attempted to be generalized to other contexts. There is only methodological support for an internal validation of the conclusions for the case of the imposed structure on the database, i.e. the chosen gravity-equation parameters’ values, the choice of the impedance function, etc. Unfortunately, given the lack of official statistics on interstate sectoral trade flows in México, there is no room for the statistical validation of the proposed method.











 nueva página del texto (beta)
nueva página del texto (beta)



