INTRODUCTION
The conventional framework of risk-taking channel of monetary policy (RTCMP) addresses the transmission mechanisms by which monetary policy may act on increasing the risk levels of financial institutions. To address risk-taking behavior, the empirical literature uses variables that represent the evolution of the risks of financial firms, and from this, it relates to the monetary policy variable. Through the relationship found, if the downward variations of the second “cause” statistically the first to vary upward, it is that the existence of a causality called “risk-taking” is established.
Nonetheless, as pointed out by the fallacy of composition, the evolution of risks of financial institutions is not enough to address financial stability (Baker, 2014; Kabundi & De Simone, 2020; Kemp, 2017; Osiński et al., 2013). The fallacy of composition arises because systemic risk has many characteristics that cause it to behave differently to the individual financial risks, the relation between two phenomena is non-linear, self-reinforcing and adaptative to the environment. These characteristics, in turn, indicate that systemic risk is a complex system.
Does this complexity, especially nonlinearity, condition how monetary policy affects systemic risk- taking? My hypothesis is that it does, the sign of impact of monetary on systemic risk can change through the time. The leverage mechanism developed by Adrian and Shin (2010) suggests that positive asset price shocks induce an increase in financial sector leverage, which in turn, generates market-wide risk pressures. Notwithstanding, what happens with negative shocks? This mechanism indicates that in this situation there is a decrease in the leverage of the system through a systematic sale of assets, which, as Danielsson et al. (2014) indicate, in times of crisis, increases systemic risk. The important thing to recognize in the mechanics of financial sector leverage is that shocks can come from changes in the stance of monetary policy.
Although more recently much empirical research has addressed the systemic risk-taking channel of monetary policy (S-RTCMP), this approach does not have considered the complexity of systemic risk. In this paper, my objective is to provide evidence about the S-RTCMP following this consideration. For this purpose, I use the TVP-VAR model with structural factor augmented (SFA-TVP-VAR), which allows me to capture the complex relationship between monetary policy and systemic risk-taking. Additionally, this model has the advantages of addressing many problems in the estimation of this monetary channel: 1) the endogeneity presented between monetary policy and systemic risk, 2) the complex behavior of systemic risk when a shock has impacted it; 3) the difficulty of measuring systemic risk.
The SFA-TVP-VAR model considers the system variables as latent and maintains monetary policy as an observable variable. For this reason, in this paper I do not try to consider one specific pressure of systemic risk and its relation with monetary policy, instead I employ financial stress and conditions indexes and I assume a latent variable called “systemic risk” drives the behavior of these metrics. Through the impulse response functions of this latent variable to shocks in monetary policy stance, I infer the systemic risk-taking channel of monetary policy.
In order to give robust evidence, I estimate the model with two different variables of monetary policy stance, the Taylor rule residual and the Wu-Xia Shadow Federal Funds Rate, changing in both cases the parameters and the priors of the model.
Considering the state of the art discussed in Section I and II of this paper, the novel contribution of this paper is to provide evidence of the existence of complexity, specifically, nonlinearity in the S-TRCMP. The posterior estimation of the model gives evidence that in longer periods the S-RTCMP behaves as usually is postulated by the current literature: in longer periods, expansive monetary policy increases systemic risk- taking. Nevertheless, in short term, before and during a financial crisis, the relationship is complex: a restrictive shock of one standard deviation in the monetary policy stance, instead of decreasing the systemic-risk taking, increases it. This evidence is consistent with what I have termed the leverage mechanism.
The outline of this paper is the following. In the first section, I lay out the micro risk-taking channel of monetary policy (M-RTCMP) framework, where I answer the question about how monetary policy shapes the risks of financial institutions from an individual perspective. Then, in section II, I explain the nature of systemic risk, and from this, why the M-RTCMP and the conventional framework of S-RTCMP are limited for addressing the impact of monetary policy on systemic risk-taking. The conclusion of this section is that it is necessary to evaluate the S-RTCMP from a perspective of complex system. In section III, I present the econometric methodology for evaluating this channel from this sight, furthermore, I show the variables of the model, the case study, and the data. In section IV, I present and explain the empirical results. Finally, the conclusions are presented.
I. THE MICRO RISK-TAKING CHANNEL OF MONETARY POLICY
Monetary policy has the capacity to change asset prices, such as the present values of loans and the prices of securities. In the first case, the rationale for this impact derives from the basic present value formula: monetary policy through the different channels established by macroeconomic theory, can influence the interest rate on loans of different maturities, therefore when a loose monetary policy condition prevails, the interest rate falls, moving up the price of loans. The prevalence of this condition for longer periods, as some economists point out (see for example Taylor (2011)), could promote the growth of bubbles in credit markets, such as real estate. Although the full responsibility of monetary policy of promoting the overall increase in housing and other loan prices is controversial in academic and political circles, we cannot ignore the impact that low rates have on loan prices. In the second case, as established by overreaction framework, Tobin’s q theory, as well as the wealth effect, downward movements in policy rates lead to increases in stock prices (Alves & Carvalho, 2020; Bernanke & Kuttner, 2005; Mishkin, 2014).
Based on this rationale, the RTCMP framework has exposes many mechanisms by which monetary policy manages to affect the risk-taking behavior of financial institutions. One of the reasons why there is more than one mechanism is that each of them assesses the reaction of different types of financial risks.
A first mechanism has to do with the paper of Borio and Zhu (2012). The idea is clear: a fall in interest rates triggers a process that increases asset prices, collateral values and profits, which in turn creates a condition in which financial intermediaries reduce their risk perception due to lower risk levels of risk metrics and increased wealth. As these authors point out, the change in risk perception then is manifested in a strategy of increased risk-taking.
A second mechanism has to do with the one postulated by Rajan (2005), he emphasizes several ways in which monetary policy could affect risk-taking, nevertheless, the general idea is the same: because of rigidity of rate of returns of asset managers, the low interest rates promoted by the central bank provoke a “search- for-yields” strategy to compensate for the situation. This behavior would then cause these agents to begin to have a greater risk appetite and, therefore, begin to grant riskier loans or invest in more volatile assets with the expectation of obtaining precisely the rates of return commensurate with the target. Although there is no explicit profitability target of banks, this asset substitution mechanism establishes that lower interest rates conditions promote a search-for-yield behavior when risk-neutral and generally risk-averse banks reduce the weight of safe assets in the portfolio composition and increase the weight of riskier assets (De Nicolò et al., 2010).
These mechanisms account for how monetary policy affects the individual or micro risks-taking. Following to Kabundi & De Simone (2020), I denominate this as the micro risk-taking channel of monetary policy (M-RTCMP). Based on these mechanisms, many researchers have produced empirical studies focusing on specific cases of national economies or covering regions as in the cases of European studies. A list of notable empirical studies, but incomplete, is presented in Table 1.
Table 1 Empirical studies of the (micro) risk-taking channel of monetary policy
| Case study | Author(s) | Financial institutions under study | Main risk type(s) measuring1/ | Risk-taking approximation variable |
|---|---|---|---|---|
| US | Segev (2020) | Commercial banks | Credit risk | Sensitivity of bank loans to loan risk |
| Alzuabi et al. (2020) | Commercial banks | Credit risk | Ratio delinquent loans to total loans; Z-score | |
| Paligorova & Santos (2017) | Commercial banks | Credit risk | Corporate loan pricing policy | |
| Eurozone and US | Altunbas et al. (2010) | Not focused on specific institutions | Credit risk, market risk | Expected default frequency; Idiosyncratic component of the CAPM model; Idiosyncratic component of the model of Campbell et al. (2000) |
| Eurozone | Neuenkirch & Nöckel (2018) | Commercial banks | Credit risk | Margins and loans standards |
| Spain | Jiménez et al. (2014) | Commercial banks | Credit risk | Delivery of loans to risky companies’ ex ante to the change in the interest rate, and capital requirements |
| France | Eid (2011) | Commercial banks | Credit risk, market risk | Forecast ratio for insolvency to total loans; standard deviations from average asset returns; z-score; change in the expected frequency of default |
| Austria | Kerbl & Steiner (2020) | Commercial banks | Credit risk | Proportion of risky clients receiving additional funds |
| China | Huang et al. (2021) | Non-bank financial institutions | Credit risk | Credit scores and credit application results of credit applicants |
| Peru | Pozo & Rojas (2020) | Commercial banks and non-banking institutions | Credit risk | Delinquency rate |
| Mexico | Morais et al. (2019) | Commercial banks | Credit risk | Volume, maturity, collateral, rate, and default of loans |
1/ Some works explicitly mention the type of risk they are measuring, and they are expressed in this table as their authors mention it; for those who do not mention it, it is inferred from their variable of approximation to risk-taking, for this, the risk classification of Heffernan (2005) was used.
These studies, albeit with some nuances, provide empirical evidence of the negative relationship between monetary policy and the micro risk-taking.
This theoretical body and its empirical support claim a clear impact of monetary policy on risk-taking, nonetheless, other economists have argued that this relation is in fact convoluted in some cases.
Dell’Ariccia et al. (2014) in their model of financial intermediation, in which main risk-taking mechanism of banks is the reduction in their efforts to monitor lenders, argue that the impact could in fact be ambiguous. When interest rate fall, there are three effects that condition the banks’ balance sheet behavior. The first has to do with the “interest pass-through effect”, which refers to the weak incentives to monitor lenders after a fall in gross returns caused by the lowering of the reference rate. The second has to do with the tendency of banks with higher levels of leverage to make less risky investments as the value of their liabilities falls, and to maximize their profits they will tend to spend more on monitoring their lenders, an effect the authors call “risk shifting”. Both effects occur in cases where there is a fixed capital structure, and it is worth noting the sign of the impact of monetary policy on risk-taking is ambiguous. However, in the case of an adjustable capital structure the sign of impact is already clear, since, in addition to the two previous effects, we must add the “leverage effect”, which refers to the tendency of banks to be leveraged without needing to hold capital when interest rates fall.
Source: own elaboration.
At the empirical level, many studies have found that, in fact, the sign of impact of monetary policy on risk-taking is positive. For example, Ngambou Djatche (2019) finds that large deviations of monetary policy from the Taylor rule can trigger an increase in the risks of banks; nonetheless, when the deviation is sufficiently low, the effect is the opposite. Similarly, Dang and Dang (2020) conclude that decreases in interest rates promote bank stability. In addition, Sarkar and Sensarma (2019) provide evidence that expansionary monetary policy decreases liquidity and market risks. This risk-taking behavior in the face of lower interest rates is in fact consistent with the effect of monetary policy on bubbles, as I explain in the following section.
Another mechanism that has indirectly pointed out the ambiguity of the relationship between monetary policy and risk-taking has to do with the leverage effect in the spirit of Adrian and Shin (2010). Unlike the previous mechanisms, this effect can account for the direct relationship between systemic risk and monetary policy. Also, I will elaborate this one in the next section.
II. SYSTEMIC RISK-TAKING AND MONETARY POLICY
Systemic and individual risks: some principles
There is no consensus about what systemic risk is, indeed, its identification and measurement subsequently face several challenges (Lars Peter, 2015). One definition that could compressively capture systemic risk is that of the European Parliament and of the Council of European Union (2010), as the risk of disruption of the financial system, with potential consequences for financial markets and the real economy (see Kemp, 2017 for discussion on the definition of systemic risk, and in particular of this one).
The individual risks differ from systemic risk in different ways. The former refers to the risks faced by individual entities in isolation, while the latter refers to the risk borne by the financial system.1 Nonetheless, this distinction does not tell us much; rather, the dynamics of both types of risk over time may account for why the two are not the same.
Increasing the risks of an institution, some of them or an entire sector can translate into an increase in systemic risk due to the interrelationships among all market participants, the failure of one firm can quickly spread to several institutions, and the larger the relative size of the distressed entity, the greater the repercussion may be at the systemic level (X. Huang et al., 2012; Kemp, 2017; Omarova, 2019). The channels of contagion, that is, the paths by which individual risks can spread through the financial system are contractual, informational, and psychological networks (Borio, 2003).
However, the same cannot be said when the risk of some institutions or of an entire industry decrease. For example, an investment bank may find that its market risk exposure is considerably high, so it may decide to sell its risky securities to meet the target of economic capital. When this occurs, this bank is effectively managing its market risk, nevertheless, systemic risk is increasing because by selling its assets, it is bidding down prices, which causes other institutions (which, may be healthy or not) to start with liquidations, this deleveraging process induces an increase in systemic risk (Mishkin, 2014).2 To what extent this process triggers a systemic event depends, firstly, on whether systemically important banks enter a distressed phase; and secondly, on whether the different systemic “pressures” are in an incubation or burst period, while in the first scenario market participants can absorb it quickly and the effect can evaporate quickly as well, in times of crisis market participants amplify the effects (Adrian & Shin, 2010; Danielsson et al., 2014), and will stop until the confidence is restored, this process is illustrated in Figure 1.
Additionally, from a cross-sectional point of view, the two types of risks differ from each other. As Beale et al. (2011) point out, following the principle of investment diversification, the individual risks faced by financial firms may decrease, however, if many institutions follow the same diversification pattern, systemic risk increases.
This shows that systemic risk and individual risks do not necessarily share the same dynamics in time and space, the former is not the simple sum of the latter.3 The relation between the two evolves over time and is nonlinear (Renn et al., 2020). This feature will be important for explaining the empirical results of this paper.
A second characteristic of the relation between individual risks and systemic risk has to do with the direction of the causal relationship. As I indicated above, a singular event can trigger a systemic event depending on the state of systemic pressures, but this does not happen overnight, but occurs through a feedback process that amplifies the singular event (Danielsson et al., 2014). This shows that the causal line not only runs from individual risk to systemic risk, but also in the opposite direction. For this reason, it is not surprising that a differentiator among all systemic risk metrics is the casual line.4
All these properties derive from the network structure of the subunits, i.e., from the individual risks that make up the system. These characteristics explain the domino effect that leads to increases in systemic risk. Nonetheless, the accumulation of systemic risk is not only endogenous in nature, but is also caused by exogenous factors. The financial system faces common risks that have the capacity to damage all financial institutions at the same time, or at least a large part of them, and these exposures can be external pressures, changes in interest rate, economic activity, and so on. The shocks from these macroeconomic risks factors to systemic risk have been referred in the literature as the “tsunami effect” leading to systemic financial distress (Borio, 2003; Kemp, 2017).
Roughly speaking, systemic risk as the system with the risks of financial institutions as fundamental subunits, is characterized as an emergent phenomenon since the interaction of the different subunits results in a system that goes beyond the sum of each component. Moreover, the relation between the system and the subunits is characterized by being nonlinear and self-reinforcing, where the subunits are interdependent and, as I will elaborate later, the system is able to respond (although not in the most rational way) to the environment. All these qualities allow us to see that systemic risk is a complex system.
Current framework: some critics
Based on the distinction between individual risks and systemic risk, the M-RTCMP approach falls into the fallacy of composition when addressing the relationship between monetary policy and financial stability. We cannot extrapolate at the financial system level what happens to individual financial institutions in the face of low interest rates, as we are neglecting many of the inherent characteristics of systemic risk.
More recently, an important amount of empirical research has addressed the problem from a systemic perspective. This approach evaluates the issue considering the impact of monetary policy on systemic risk “pressures”. The findings are in line with what is stated in the RTCMP framework: expansive interest rate shocks increase systemic risk (Bubeck et al., 2020; Colletaz et al., 2018; Faia & Karau, 2021; Jin & Nadal De Simone, 2020; Kabundi & De Simone, 2020; Kapinos, 2021).
Nonetheless, this current S-RTCMP approach has a limitation: it does not consider the complex characteristics of systemic risk. The main question here is to what extent this consideration is important.
The M-RTCMP establishes the theoretical framework on how low interest rates promoted by central banks induce greater risk-taking by financial institutions, nevertheless, what happens when monetary policy shifts from an accommodative to a more restrictive stance? The M-RTCMP mechanisms explained in Section II do not explicitly state what happens in this situation. Moreover, what happens at the systemic level when interest rates rise sharply? This is when an additional mechanism becomes important, the leverage effect.
One of the principles underlying the “lean versus clean” debate is that increases in reference interest rates can burst a financial bubble. The transmission mechanisms of this impact are varied, for example, through the leverage of financial institutions. Adrian and Shin (2010) argue that when positive shocks in asset prices strengthen the asset side of financial intermediaries’ balance sheet, they adjust the resulting leverage level upwards by buying more assets and taking on more debt to finance these purchases. This in turn affects asset prices (due to higher demand), which in turn paves the way for the possibility of a self- reinforcing price cycle. In the opposite scenario, when a negative shock lowers asset prices, the leverage level of financial intermediaries increases, then they seek to return to target or, more actively, some seek to lower the target leverage level. Just as with positive shocks, the deleveraging process opens the way to a perverse self-reinforcing loop of falling prices.
The important feature to recognize in the leverage effect is that the shock to asset prices can potentially be fueled by monetary policy: the self-reinforcing process can be fueled by a loose monetary policy for a long period and an abrupt tightening in the interest rate stance.
As Adrian and Shin (2010) recognize, this procyclical behavior in leverage levels from balance sheet changes is unfamiliar to financial firms, because in terms of them, they drive leverage by risk management. Empirical evidence shows that the Value-at-Risk (VaR) is countercyclical, and since the capital banks held by banks is positively linked to this metric, then the leverage becomes cyclical.
When the interest rates fall, asset prices rise, so the overall VaR decreases. Since the economic capital of banks is positively related to the level of VaR, a lower level of VaR implies a lower level of capital. Due to the inverse relationship between leverage and capital, a decrease in the latter implies an increase in the former. Likewise, systematic increases in the level of leverage in the financial system imply a greater demand for assets, which for longer periods eventually triggers a bubble. This becomes a systemic risk-taking because financial institutions are increasing the likelihood of system-wide disruption, as they are inflating the value of assets beyond their fundamentals, which, when they return to their value, will cause everyone to start having balance- sheet problems.
Conversely, when interest rates rise, this transmission mechanism operates in the opposite direction. As pointed out by Danielsson et al. (2014), a negative shock in asset prices does not imply a major problem in normal times, nevertheless, in periods of crisis, it triggers a feedback process that amplifies the initial shock, prices fall dramatically affecting the health of financial system. In this context, the linearity in the relationship between monetary policy and micro-risk taking is maintained, interest rates hikes cause financial institutions to begin to dispose of their risky assets, increase their capital and lower their VaR levels, which implies a desire not to take on risk. Nevertheless, in the end they are taking risk, not of an individual nature, but of a systemic nature. By divesting their assets, they are driving down asset prices, which ends up affecting themselves, and the financial system in general.
Additionally, both environments, when the bubble develops and when it bursts, as shown by Brunnermeier et al. (2020) and Danielsson et al. (2014), imply an increase in systemic risk. I have summarized this mechanism in Equations 1 and 2.
where
These properties in the relationship between policy rates and systemic-risk raking are directly inherited from the characteristics of systemic risk. For this reason, it is important to approach the issue with nonlinearity in mind.
Having clarified that the systemic risk-taking channel of monetary policy behaves differently depending on the prevailing conditions of systemic risk (whether it is in the incubation or bust period), the next question is how to address it.
Since the Great Recession (GR) there has been a great effort in academic and political sectors for monitoring systemic risk, for example, through the expected capital shortfall of banks relative to the regulatory limit, in the face of a stock market crash (Brownlees & Engle, 2017), or given that the aggregate capital of the system has fallen below the regulatory fraction (Acharya et al., 2017); the change of the VaR of financial system (calculated from a market index) conditional on the distress of an individual institution relative to the median state of that entity (computed from the return performance of that entity in the stock market) (Adrian & Brunnermeier, 2016); metrics based on the multivariate density of default probabilities (inferred from CDS spreads or Out-of-the-Money option prices) of each institution comprising the system (Segoviano & Goodhart, 2009); the probability of moving to a high volatility regime (based on financial variables and CDS spreads data) (Abdymomunov, 2013); financial stress and conditions indexes, which attempt to summarize the evolution of key factors that characterize a financial crisis (S. Brave & Butters, 2012; Hakkio & Keeton, 2009; Kliesen & Smith, 2010; Oet et al., 2015), among others.
All these metrics address a different manifestation of systemic risk, such as undercapitalization, maximum loss, contagion capacity, probability of a financial crisis, and financial markets conditions, and I called them as “pressures” in this paper to differentiate them from the “tsunami effect” variables, since the former do not become independent or external variables of systemic risk but are “faces” of the latter. Another way to understand this variety of measures is to observe that the financial system is composed of many elements, it is not only constituted by economic agents (banks, shadow banking, central bank, regulators, payment systems, etc.), but rather by markets (transactions of instruments) and functions (Oet et al., 2015), any measure that shows the aggregate risk of these can be considered as an financial soundness indicator, because, although they may appear different in form, one latent variable is driving their behavior: systemic risk.
Currently, one of the main approaches of central banks to monitor financial stability and systemic risk is to observe the state of the financial markets. The main advantage of this methodology is that the state of all financial markets can be summarized in a single measure.
Risk-taking, as can be deduced from the literature review on transmission mechanisms, is a “latent” variable, i.e., it cannot be measured directly as it is a social behavior. Nonetheless, the RTCMP framework has addressed this problem by considering a variable that can reflect this behavior and then relates it to the monetary policy variable to infer a risk-taking channel.
III. THE ASSESSMENT
Based on the literature review and the elements that characterize systemic risk, I identify at least three challenges for assessing the S-RTCMP: 1) the endogeneity between systemic risk and monetary policy;
2) the self-reinforcing and nonlinearity of systemic risk once a shock has occurred, and their possible implications for the S-RTCMP; 3) the complexity in measuring systemic risk.
For this reason, a model that attempts to capture the S-RTCMP should consider these points. In this section, first, I show the model that have the ability to address these issues; second, I present the variables in the system of equations that I use to infer the S-RTCMP; finally, I present the data and their transformations prior to estimation.
The model
For the first challenge, VAR models have proven to be an excellent alternative to alleviate the endogeneity problem among all variables of a system. Furthermore, VAR models consider the feedback between a variable and its past values, which helps to identify the self-strengthening of the variable. Between VAR models is the Structural Factor Augmented VAR (SFAVAR) model in the spirit of Belviso and Milani (2006), which provides a technique for modeling a system in which the elements are latent variables. Nonetheless, the latter approach does not have the ability to identify the nonlinear relationship between the variables that compose the system. Because of this limitation, it is necessary to move towards the time-varying parameters (TVP) framework which, for estimation purposes, makes extensive use of Bayesian methodology.
Korobilis (2013) proposes a model that extends the FAVAR model in the spirit of Bernanke et al. (2005) by changing the parameters of the VAR equation by other time-varying variables. The methodology developed by Korobilis (2013) also allows him to estimate a Structural Factor Augmented TVP-VAR (SFA-TVP-VAR) model.
For the purposes of this section, the SFA-TVP-VAR model is formulated as follows,
where
This model follows the representation proposed by Korobilis (2013), nevertheless, the methodology proposed by this author faces a major challenge: as the system contains more variables, the covariance matrix for the states becomes near singular. This is an important issue in addressing the S-RTCMP, as systemic risk is caused by many factors.
There are many techniques in the literature to alleviate this problem; in this paper I address it using the approach of Chan et al. (2020), which consists of reducing the number of states driving the VAR varying coefficients.
Stacking all the parameters
where these parameters, at each time t, are constituted of a constant part and driven by factors,
and the factors evolve over time as random walks,
with
The state space dimension reduction occurs when the rank of
This model allows me to identify in the S-RTCMP the implications of the inherent characteristics of systemic risk once a monetary policy shock has occurred. And capturing this relationship, in turn, allows me to provide evidence on the nonlinearity in systemic risk and individual risks. I will elaborate on this in the results section.
Variables, ordering, prior and data
Monetary policy
I take the U.S. case to study the S-RTCMP, and the reference period I use as sample runs from January 1994 to February 2023. During this period, the main instrument for conducting monetary policy has been the federal funds rate. Nonetheless, this variable may be endogenous to macroeconomic variables, which biases the empirical results in approximating the impact of monetary policy on risk-taking behavior (Delis et al., 2017; Segev, 2020). Although in the VAR model endogeneity can be easily addressed, for more robust results I will use, as in other empirical research, many indicators that can reflect the “monetary stance”.
In order to find robust results, I estimate the SFA-TVP-VAR model with two different metrics of monetary policy stance. The first variable I use is the Taylor rule residual. Assuming the identification of Taylor (1993), the Taylor rule is defined as
where the
Finally, as monetary stance variable I employ the Shadow Rate of Wu and Xia (2016), which has the advantage of measuring the central bank rate beyond the lower bound and considering the other tools used by the Fed to affect the economy. One way to interpret this indicator is that when it is negative it indicates a loose monetary policy, and when it is positive and high, indicates a restrictive stance.
In the remainder of this paper, when I mention the variable "monetary policy stance", I am referring to both variables, the Taylor Rule Residual and Wu-Xia Shadow Federal Funds Rate. In Figure 2, I show the variables of monetary stance and the effective federal funds rate.
Systemic risk
Systemic risk is a “latent” variable; however, it can be inferred by monitoring the different systemic pressures that reflect the condition of the agents, markets, or functions that comprise the financial system. In this paper I will infer the state of systemic risk based on the financial market conditions. As I discussed earlier, one of main measures used today by central banks to monitor financial stability are the financial market conditions and stress indexes, which are calculated from publicly available data.
As discussed in the previous section, systemic risk is measured by pressures in the system. In financial markets, these pressures manifest in the form of a generalized widening of the gap between returns on risky assets and risk-free assets in the credit, funding and real estate markets; deviations of financial sector equity returns from the equity market; equity market crashes; divergence of covered interest rate parity in the foreign exchange market, indicating disruptions in international funding markets; reduced liquidity in the interbank funding market; changes in the yield curve spread; and the coordinated movement of all these indicators.
The idea behind the stress indexes is that systemic risk materializes in a change of state or equilibrium, from a positive to a crisis state (Hendricks et al., 2007; Kliesen & Smith, 2010; Oet et al., 2015), which is reflected in specific levels of the key variables mentioned previously (Hakkio & Keeton, 2009).
Furthermore, related to the stress indexes, there is the approach that seeks to assess the state of the financial system by monitoring the evolution and interconnectedness of financial variables regarding their long-term trend or how they evolve with respect to crisis conditions, this is the approach of financial conditions indexes.
Both types of indexes differ in their objectives, the financial stress indexes seek to assess the state of risk of the financial system, while the financial condition indexes seek to report on whether the state of financial markets is in a crisis or normalcy episode.
In this paper, I assume that financial conditions and financial markets stress are driven by an underlying variable called “systemic risk”. For this purpose, I use the Kansas City Financial Stress Index, St. Louis Fed Financial Stress Index, and Chicago Fed Adjusted National Financial Conditions Index. I show these indexes in Figure 3.
Other Variables
As I discussed in Section II, systemic risk can be generated internally through existing networks between subunits (Borio, 2003; Danielsson et al., 2014; Kemp, 2017). Empirically, this source has been approached from the network science, with methods such as cascades, graph and percolation models, which requires explicit consideration of the microstructure of the financial system (Abergel et al., 2013; Baruník & Křehlík, 2018; Hurd, 2016). Integrating these models with the macroeconometric model used in this paper involves studying how a shock propagates through time and among the elements that compose the financial system. Such an amalgamation is beyond the scope of this paper. Nevertheless, this disadvantage can be remedied since the SFA-TVP-VAR model considers lags of the systemic risk variable, this feature may be trivial in normal times, however in crisis episodes, the feedback loop between systemic risk is a manifestation of the interconnectedness factor.
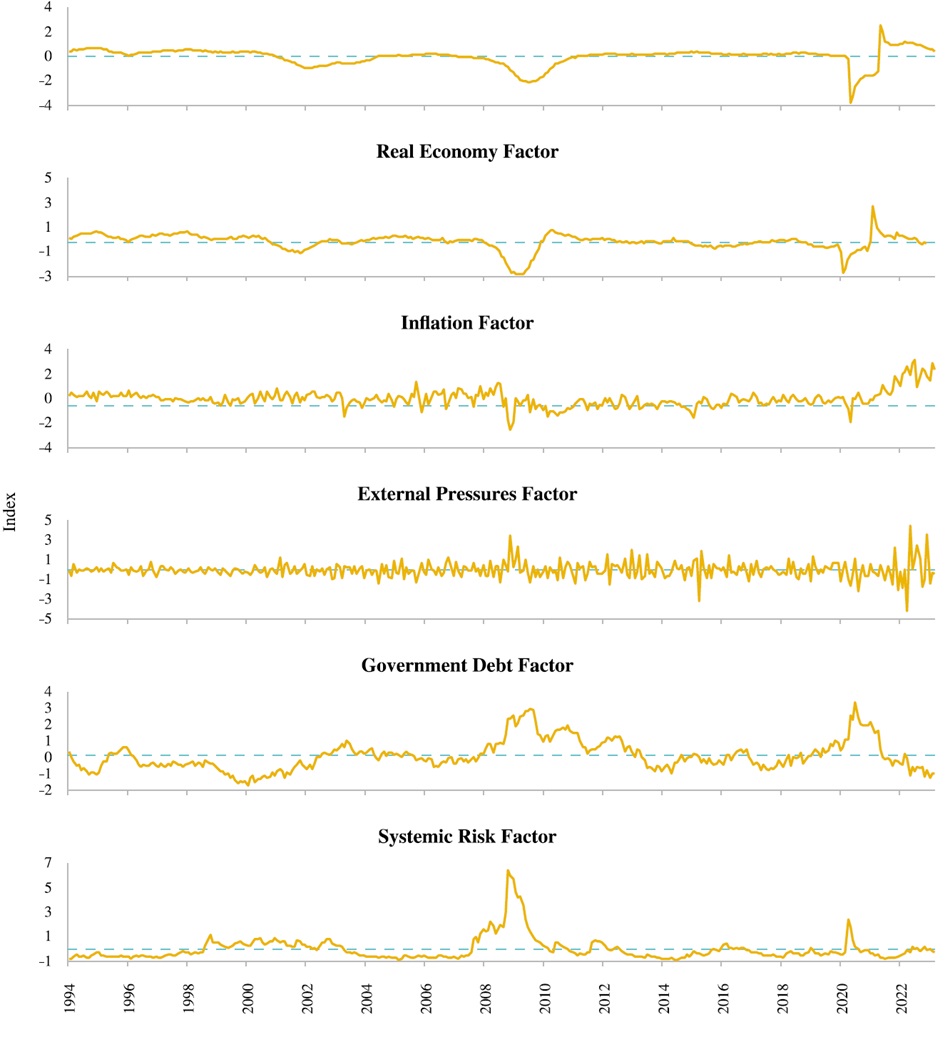
Additionally, it is important to consider that systemic risk has causes from outside the financial system. The impact of these sources has been referred to in the literature as the “tsunami effect” (Kemp, 2017), and the empirical evidence of the M-RTCMP (see Table 1) has pointed out that these factors should be considered in the estimation process. To consider the “tsunami effect” in the estimation of the S-RTCMP, I add to the system of equations the factors of real economy, inflation, external pressures and government debt, which in turn, are estimated through an extensive list of series.
Ordering, parameters and priors
In the empirical analysis with Structural VAR models, it is usual to assume an ordering of the system of variables. For the model with monetary policy stance as Taylor rule residual, I assume the following ordering of the factors: 1) labor market factor; 2) real economy factor; 3) inflation factor; 4) external pressures factor;
5) monetary policy stance; 6) government debt factor; 7) systemic risk factor. Additionally, I assume the following parameters:
For the prior, in this first model I use the SSVS specification as in Chan et al. (2020), but without the Minnesota prior,
where
In the second model, where the monetary policy stance is the Wu-Xia Shadow Rate, I use a more limited system of equations. I employ the following system in this order: 1) real economy factor; 2) inflation factor; 3) monetary policy stance; 4) systemic risk factor. And I set the following parameters:
In this second model, I employ the Minnesota prior with the following parameters:
For the estimation of both models, I follow the two-step process in the spirit of Korobilis (2013), I first approximate the factors through the PC method, then, I estimate the parameters of the VAR equation through the methodology of Chan et al. (2020), changing the VAR to a VEC form and restructuring it. Since the parameters
Data
The series that I use to model the factors and monetary policy are listed in Appendix A. All the data I employ are from FRED, except for the Wu-Xia Rate, which is from the webpage of Federal Reserve Bank of Atlanta. All labor market, real economy, inflation, external pressures and public debt series are on a monthly basis. Regarding the Taylor rule series, the only variable that does not have a monthly basis is the output gap, and in order to estimate the missing values, I employ the cubic spline method. The St. Louis Fed Financial Stress Index and the Chicago Fed Adjusted National Financial Conditions Index series are in a weekly frequency, to transform them to a monthly basis I take the simple monthly average. The Kansas City Financial Stress index is monthly.
I transform some of these series to induce stationarity. The details of the transformation of each series can be seen in the index of the last column of the table in Appendix A.
IV. RESULTS
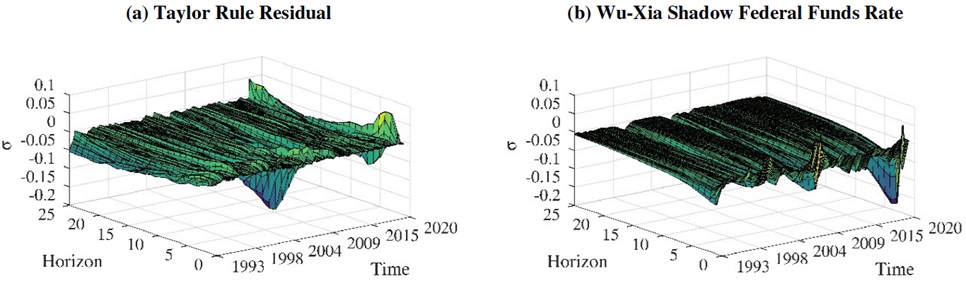
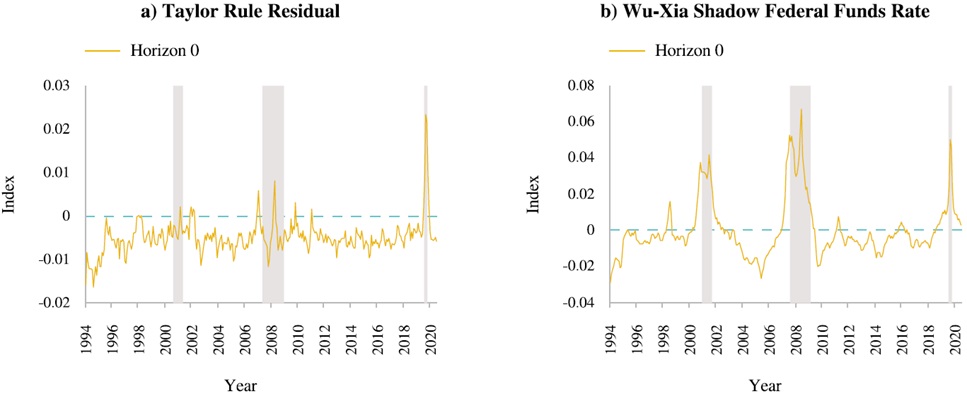
The systemic risk factor and the different metrics described in Section 4 are presented in Figure 4. To identify the S-RTCMP, I rely on the dynamic impulse-response functions obtained from the SFA-TVP-VAR model. Since all system variables were standardized prior to estimation, the results of these functions indicate a one positive standard deviation shock and a response in standard deviation points.6 The impulse-response functions of monetary policy stance variables to systemic risk for 25 horizons are presented in Figure 5; in more detail, I present these functions at different horizons, in Figure 6 I show the response at
Sources: author’s calculation based on FRED and Federal Reserve Ban of Atlanta data.
Figure 4 Factors
Source: author’s calculation based on FRED and Federal Reserve Bank of Atlanta data.
Figure 5 Impulse response functions of systemic risk factor to monetary policy shocks
Source: author’s calculation based on FRED and Federal Reserve Bank of Atlanta data.
Figure 6 Immediate response of systemic risk factor to monetary policy shock
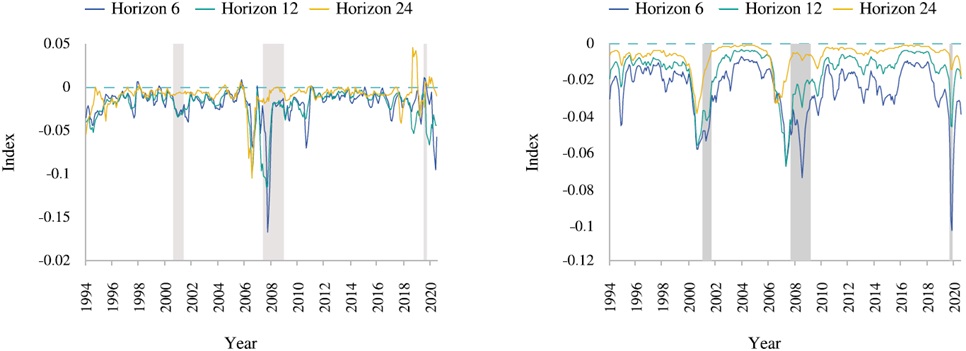
The results of the two models presented in Figure 7 show that in longer periods the impact of monetary policy is negative, which is in line with the current S-RTCMP framework (Bubeck et al., 2020; Colletaz et al., 2018; Faia & Karau, 2021; Jin & Nadal De Simone, 2020; Kabundi & De Simone, 2020; Kapinos, 2021), i.e., low interest rates promote risk-taking behavior of an entire system. Nonetheless, in short-term periods we see that the impact is different, in fact, it is positive in some periods.
Source: author’s calculation based on FRED and Federal Reserve Bank of Atlanta data.
Figure 7 Response of systemic risk to monetary policy shock at different horizons
First, in the period preceding the 2001 crisis, characterized by the development of the dot-com bubble, the Figure 6, mainly in the graph with the monetary policy stance as Wu-Xia rate, shows peaks indicating that a positive standard deviation of the monetary policy stance from the its mean, i.e., a tightening of interest rates, has a positive impact on the systemic-risk taking.
Something similar happens with the period prior to the 2008 financial crisis, in the two graphs in Figure 6, prior to the recession we see how the sign of the impact of one standard deviation of the monetary policy stance from its average, i.e., a restrictive stance on interest rates, to the systemic risk-taking changes from negative to positive, with peaks even before the crisis begins.
However, the systemic risk-taking channel of monetary policy does not behave in the same way in a crisis whose origins are outside the financial system as in a crisis whose factors are inside the system. In the period before the COVID-19 pandemic, the two pictures in Figure 6 do not indicate any peak; simply, when the recession begins, the positive impact of a tight monetary policy on systemic risk-taking starts to be very pronounced, and then drops abruptly.
The positive relationship between a restrictive monetary policy and systemic risk-taking in periods before and during a crisis whose origin is inside the financial system is consistent with the leverage mechanism summarized in Equation 1. This evidence has important implications for monetary policy, assuming that a central bank could identify an increase in systemic risk, how should respond to these episodes? The evidence presented previously indicates that if the central bank tightens interest rate levels to decrease the identified systemic risk, the result may be counter-prudent, since instead of decreasing this risk, it would be causing it to increase further.
Indeed, this relationship in periods of crises adds an additional cost to the lean position in the “lean versus clean” debate. Although the cost of cleaning up a financial crisis after it has occurred could be high in terms of damage to the real economy (Mishkin, 2011, 2014), especially if this crisis has its origin in credit bubbles, adopting a “lean against the wind” policy could also be detrimental, because it further amplifies systemic risk that ultimately harms the real economy.
Finally, it is worth noting that although the TVP-SFA-VAR model used in this paper cannot directly elucidate the feedback process between systemic risk and its subunits, we can indirectly infer this complex relationship through the impulse-response functions of systemic risk to self-induced shocks.
V. CONCLUSION
The nature of systemic risk is characterized by several elements, such as the interdependence of the subunits that comprise it, the non-linearity between the latter with the behavior of the whole, the self-reinforcement between the whole and the subunits and the response to the environment in which the system operates. The M-RTCMP framework analyzes the behavior of the subunits in a monetary policy environment with a loose stance and although it is very important to analyze this relationship, this view is limited when studying the risk behavior of the financial system as a whole, since it does not consider the features that characterize the latter.
Considering systemic risk as a complex system has important implications for the way we think about the relationship between monetary policy and financial instability, from this angle we can observe the impact of interest rates on systemic risk-taking.
My objective in this paper has been to provide evidence of a systemic risk-taking channel of monetary policy considering the complex nature of systemic risk with the hypothesis that this relationship is complex, specifically, nonlinear. Using the SFA-TVP-VAR model, which helps us to infer the relationship between latent variables, the results provide evidence in favor of the hypothesis: it exists a complexity in the way that S-RTCMP operates, the relationship between systemic risk-taking and monetary policy is nonlinear over time and adapts to the economic environment, while in normal times we can observe that restrictive shocks in the monetary policy stance led to a decrease in the systemic risk-taking, in uncertain periods, they imply greater risk-taking by the financial system.
This evidence is consistent with the mechanism of leverage: a positive shock, which may have its origin in an expansionary monetary policy, decreases the level of risk measured by the risk metrics of financial institutions. Specifically, if we consider the overall VaR of financial firms, we see that it decreases, which in turn reduces the economic capital held by institutions. Through the inverse relationship between capital and leverage, a decrease on the capital side implies an increase on the leverage side. This leverage cycle has the potential to create a bubble if the lower interest rate stance is maintained for extended periods, which in turn, can create further systemic risk pressures. In this environment or in a crisis period, however, a sharp increase in interest rates does not necessarily means a reduction in systemic risk levels, as a deleveraging cycle promotes greater instability in financial markets, which tends to increase the risk of a disruption of the financial system.
Derived from these results, we can see that the policy of “lean against the wind” has an additional cost: an increase in systemic risk. Additionally, it is important to highlight that there are still more questions to be addressed from these results, such as their implications for the relationship between macroprudential policy and monetary policy, the design of better instruments for the prevention of systemic crises, and even the way of doing macroeconomics, since the financial system has proven to be one of the triggers of economic fluctuations.











 nueva página del texto (beta)
nueva página del texto (beta)






