1. Introducción
Los Modelos Digitales de Elevaciones (MDE) del terreno son registros digitales de la superficie topográfica desnuda que pueden producirse por diversas técnicas (p.ej. LiDAR, fotogrametría aérea, teledetección, etc.). Los MDE son la base de otros modelos derivados, como los de pendientes, orientaciones, insolación, redes de drenaje, cuencas visuales y aportadoras, etc., que pueden derivarse fácilmente de ellos por medio de operaciones SIG. Por todo ello tienen aplicación en numerosas disciplinas como la agricultura, la biología, la geología, la climatología, telefonía, defensa nacional, etc., donde sirven para actividades de análisis, modelización y toma de decisiones.
Dada la importancia de los MDE su calidad posicional (altimétrica) debe ser conocida. Son numerosos los estándares y métodos para la estimación y control de la exactitud posicional (p.ej. ver la publicación 557 del IPGH). Algunos de estos estándares ofrecen alguna directriz particular para el caso de la altimetría; sin embargo, todos ellos se basan en la utilización de puntos bien definidos para realizar las evaluaciones. Este último aspecto no es adecuado al caso de MDE, especialmente cuando se registran como una teselación del espacio (grid). En Mesa-Mingorance y Ariza-López (2020) y en Polidori y El Hage (2020) se realizan amplias revisiones críticas de los métodos de evaluación de la exactitud aplicados al caso de los MDE y es de destacar que el enfoque mayoritario se basa en la utilización de puntos, con independencia del estándar o método que se aplique.
En el caso de datos geoespaciales de tipo lineal, como son las vías de comunicación, las líneas de costa o las redes hidrográficas, en los que no siempre es posible encontrar puntos bien definidos u homólogos entre dos representaciones de una misma realidad, se han propuesto métodos de evaluación específicos basados en técnicas de orlado, como son el método del orlado simple (MOS) (Figura 1a) y el método del orlado doble (MOD) (Figura 1b), el método VIM (Mozas-Calvache y Ariza-López 2011), etc. En Ariza-López y Mozas-Calvache (2012) se puede encontrar un análisis esclarecedor basado en dados sintéticos.
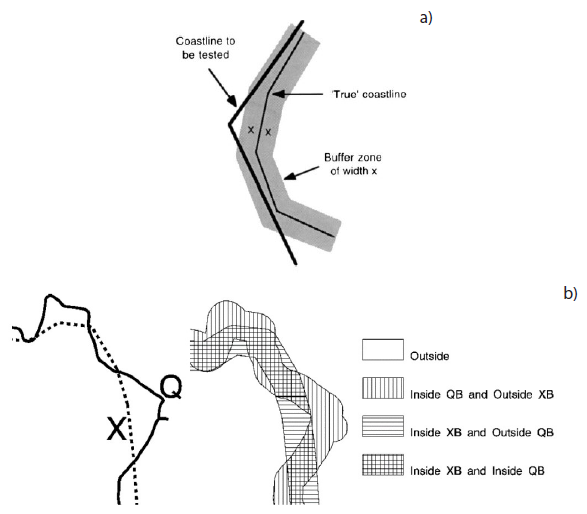
Figura 1 a) Método del orlado simple (MOS) (Fuente: Goodchild y Hunter, 1997); b) Método del orlado doble (MOD) (Fuente: Teveite, 1999).
En este trabajo se propone aplicar la idea del orlado, simple y doble, sobre superficies con vistas a comparar el comportamiento altimétrico de dos conjuntos de datos MDE. Con esta nueva perspectiva se soslaya el inconveniente de no disponer de puntos bien definidos en el caso de MDE de tipo grid y, además, permite ser aplicada en el contexto natural de la realidad que se analiza, que es el de una superficie. Los métodos basados en el orlado de superficies MDE podrán ser utilizados para comparar dos conjuntos de datos MDE, o un producto y una referencia que sirve para su control.
Este documento se organiza de la siguiente manera, tras esta introducción la siguiente sección (2a.) presenta los métodos de orlado y su adaptación al caso de MDE tomando como caso de uso un MDE sintético. La sección tercera desarrolla una breve discusión y, finalmente, se incluyen las principales conclusiones del trabajo.
2. Métodos de orlado adaptados a MDE
A continuación se presenta la adaptación de los dos métodos al caso que nos ocupa. Primeramente, se presentará un esbozo de la idea en la que se basa el método en su aplicación al caso original de elementos lineales, y luego se comentará cómo adaptarlo al caso de superficies MDE.
2.1. Orlado simple
Dado que el MOS fue diseñado para elementos lineales, para su explicación vamos a considerar aquí dos de ellos: Q (referencia) y X (elemento a analizar). El MOS consiste en generar orlados de semi-anchura wi alrededor (ambos lados) de la línea Q (denotados por Qwi), e ir contabilizando el porcentaje de la línea X que se encuentra incluido en ese orlado Qwi. El parámetro w tomará valores desde aproximadamente cero hasta aquel que permita incluir la longitud total de X. El método se puede aplicar a una línea, tal y como se ha explicado, o a un conjunto de líneas Qj y Xj, obteniendo un resultado agregado de todas ellas para cada wi. Si se considera el porcentaje de longitud de línea que se va incluyendo para cada valor de w, %L=f(w), se dispone de una función de distribución observada que define el fenómeno de interés: porcentaje de inclusión de las líneas X frente a las anchuras del orlado de las líneas de referencia.
El método descrito en el párrafo anterior es directamente trasladable al caso de MDE. Primeramente, consideraremos dos superficies S1 y S2, tal que S1 actúa como referencia y S2 como producto. Además, deberemos suponer que la incertidumbre planimétrica es despreciable, de tal manera que el orlado se puede realizar directamente sobre la componente altimétrica. Para el caso de MDE de tipo grid, como el que nos ocupa, el proceso de aplicación del MOS es sencillo, basta con calcular el modelo de diferencias DIFF = ABS(S2-S1), ordenar de menor a mayor los valores de discrepancias (errores) obtenidos, y contabilizar el área que se va acumulando para cada semi-ancho wi. La curva así obtenida tiene las mismas propiedades que la que se genera en el método original para elementos lineales, de tal manera que se puede aplicar a un MDE o a un conjunto de “parches” (superficies parciales de un MDE de mayores dimensiones).
2.2. Orlado Doble
Continuando con los dos elementos lineales, Q (referencia) y X (elemento a analizar), presentados anteriormente, el método del orlado doble consiste en generar orlados de semi-anchura wi alrededor (ambos lados) de las líneas Q y X. En este caso, la propuesta de Tveite y Langaas (1999) es contabilizar varias medidas que evolucionan con wi. Siendo Xwi el área del orlado sobre X para el ancho wi, y Qwi el área del orlado sobre Q para el mismo ancho, estas medidas se corresponden con las siguientes áreas: Área (Xwi ∩ Qwi), Área (Xwi ∩
Se ha de considerar el mismo supuesto que en la sección 2.1 para el MOS respecto a la componente de incertidumbre planimétrica. Además, el método descrito en el párrafo anterior debe ser ligeramente adaptado para su aplicación al caso de MDE de tipo grid. Considerando que S1 actúa como referencia y S2 como producto, se procede a establecer el orlado incremental sobre las dos superficies. Para el análisis con datos de tipo grid conviene introducir el concepto de voxel especificado para este contexto: volumen que tiene como sección central una celda del MDE de tipo grid sobre cuya cota se trabaja, y una altura wi a cada lado (arriba y abajo) de esa celda. Al trabajar con dos superficies S1 y S2 para cada posición (celda) se consideran dos voxels y hay que prestar atención a las siguientes situaciones:
Sin intersección de los voxels de los dos orlados. Significa que la distancia vertical entre S1 y S2 excede a 2xwi.
Intersección parcial de voxels de los dos orlados. Significa que la distancia vertical entre S1 y S2 es menor que 2xwi. Si la distancia entre S1 y S2 es nula, existirá una coincidencia completa de los voxels. En este caso, para un wi dado y una posición concreta en el MDE, el grado de intersección entre los voxels de S1 y S2 se puede considerar como una aproximación fuzzy o probabilística.
De esta forma y manera gestionamos en el caso de MDE la propuesta de áreas que realizaban Teveite y Langaas (1999) para trabajar con líneas pudiendo obtener curvas distribucionales relativas a la inclusión que son en todo semejantes.
3. Resultados de aplicar los métodos de orlado adaptados a MDE
Como se ha indicado anteriormente, los MOS y MOD se han aplicado al análisis de la exactitud posicional de elementos lineales, por ello, para proceder a su aplicación novedosa al caso de MDE, en este trabajo se utilizarán unos datos sintéticos tal que permitan diseñar y controlar el comportamiento que se analizará por medio de esta herramienta de análisis.
El conjunto de datos sintéticos es el que se visualiza en la Figura 2. Como se puede observar, se trata de dos superficies: S1 y S2. S1 es de carácter sinusoidal y se compone de una portadora de menor frecuencia sobre la que monta otro patrón sinusoidal de mayor frecuencia. S2 es un plano de pendiente constante. S1 se puede considerar como una mejor aproximación a la realidad dado que posee mayor detalle, mientras que S2 se puede considerar como una generalización. De esta forma, en el caso de un control de la exactitud posicional, S1 actuaría como referencia y S2 como producto. La configuración de S1 y S2 permite observar qué ocurre con las ondulaciones y el sesgo que existe entre las dos superficies.

Figura 2 MDE sintéticos considerados: S1 (referencia) en tonos verdosos y S2 (producto) en tonos rojizos.
3.1. Orlado simple
Aplicando el sencillo procedimiento indicado en el apartado 2.1, se puede obtener como resultado la curva que se presenta en la Figura 3. Esta curva representa función de distribución del área de superficie del MDE respecto a la semi-anchura del orlado wi. Una curva como esta permite:
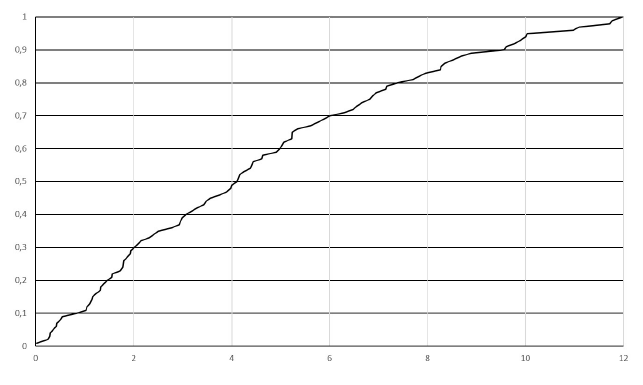
Figura 3 Resultado del método del orlado simple. % de inclusión de la superficie de S2 para cada semi-ancho de orlado (wi).
Reconocer la presencia/ausencia de valores atípicos. Un valor atípico en nuestro caso sería un valor excesivamente grande de discrepancia entre S1 y S2 y se correspondería con la presencia de picos o pozos. Esta presencia generaría la necesidad de un valor muy grande de w para conseguir su inclusión y un aplanamiento asintótico de la curva cercano al valor de la unidad en el eje vertical (100% de inclusión). Como se observa en la Figura 3, este no es el caso, por lo que no hay presencia de atípicos.
Reconocer la presencia/ausencia de sesgo vertical. El sesgo vertical en este caso significa que un MDE tiene predominancia altimétrica sobre el otro. En este caso, el valor de w(0,5), el w correspondiente al 50% de inclusión, se compara con 0,5xw(1), la mitad del correspondiente al 100% de inclusión. La posición de w(0,5) respecto a 0,5xw(1) nos determina el sentido del sesgo, y la diferencia entre ellos, su magnitud. En nuestro caso, se evidencia sesgo (S2 >S1) y en el orden de 2m puesto que 0,5xw(1)= 6 m, w(0,5)= 4 m, 0,5xw(1) - w(0,5)= 2 m. Además, se evidencia por un desequilibrio del 20% de superficie: F(0,5xw(1)) - F(w(0,5)) = 0,7 - 0,5 = 0,2.
Determinar la incertidumbre, bien estableciendo un percentil de interés (p.ej. 70%) y determinando la distancia correspondiente (dP=70%= 6 m), o bien estableciendo una distancia (d= 8 m) y determinando su percentil correspondiente (84%).
La disposición de la curva obtenida es totalmente equivalente a la generada por el MOS sobre líneas, y su interpretación exactamente igual, pero sustituyendo porcentaje de longitud de línea por porcentaje de superficie, como ya se ha indicado. Igualmente, se puede aplicar a un único conjunto de datos MDE, o a varios conjuntos de datos MDE de manera agregada. Por otra parte, la curva presentada en la Figura 3 es totalmente equiparable a la utilizada por Ariza-López y col. (2019) para aplicar un método de control posicional por puntos que se basa en la aplicación de varias tolerancias y un modelo multinomial para modelar los porcentajes de casos de error, por lo que este método puede ser aplicado directamente a este resultado.
3.2. Orlado doble
La aplicación directa del método indicado en la sección 2.2 permite obtener diversos resultados, algunos de los cuáles se presentan a continuación. En orden a entender la secuencia del proceso, la Figura 4 presenta una secuencia de los orlados de S1 y S2 conforme se incrementa w = [1, 2, 3, 4] m. En blanco aparecen las celdas para las que no hay intersección de voxels para el wi considerado. En una gama de colores del rojo al verde aparecen las celdas en las que hay intersección parcial. Cuanto menor es el porcentaje de intersección los tonos son más rojos. Cuanto mayor es el porcentaje de intersección los tonos son más verdes. Estos resultados espaciales también se pueden expresar mediante curvas, como se realiza en la Figura 5. En esta figura el eje horizontal se corresponde con el porcentaje de intersección entre voxels y el eje vertical al porcentaje de área del MDE. En ella se observa que todas las curvas presentan un comportamiento tembloroso, el cual se debe a la configuración ondulada de S1. Además, también se puede distinguir dos grupos de curvas; por un lado, las que parten de valores cercanos al cero del eje horizontal, que se corresponden con valores de w bajos (p.ej. w=[1, 3, 5] m) y que, por tanto, pueden no llegar a tener una intersección de voxels al 100% y que tampoco cubren el 100% del área del MDE, y por otro, aquellas que parten de un porcentaje de intersección medio y que sí llegan a cubrir toda la superficie del MDE, como es el caso de las curvas correspondientes a w=[10, 15, 20] m. El menor valor de w que envuelve a S1 y S2 generará una curva vertical a partir de un porcentaje de intersección alto. Esta gráfica permite determinar el valor de w que ofrecería un porcentaje determinado de intersección de voxels, por ejemplo, si se quiere partir de, al menos, un 50% de intersección se requiere un valor de w entre 10 y 15 m (en este caso 12 m). Además, también permite establecer el valor de w que permite cubrir un porcentaje dado de superficie del MDE (p.ej. 70%) y con el que se supere un nivel mínimo deseado de intersección de voxels determinado (p.ej. 80%). Así, para este caso, será la curva correspondiente a w= 15 m pues es la más cercana al punto (0,8; 0,3) de la gráfica. Es decir, la semiamplitud w =15 m nos asegura que el 70% de la superficie del MDE esté cubierta si se consideran todos los voxels cuya intersección es <=80%. El grado de confianza será mayor cuanto mayor sea el valor de % de intersección de voxels (eje X) en el que comienza la curva, en el caso de w=15 comienza en el 60% lo cual es un alto grado de confianza.
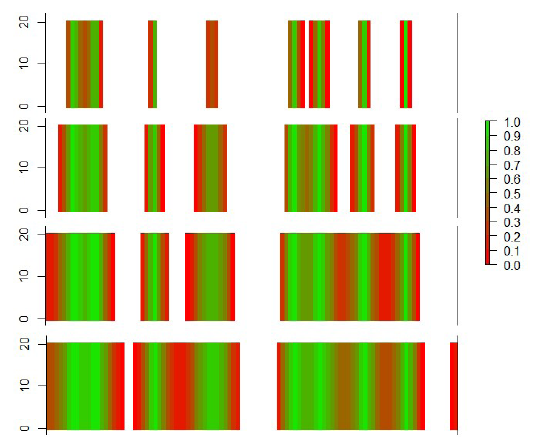
Figura 4 Evolución de las intersecciones de los voxels de los orlados de S1 y S2 para w = [1, 2, 3, 4] m.
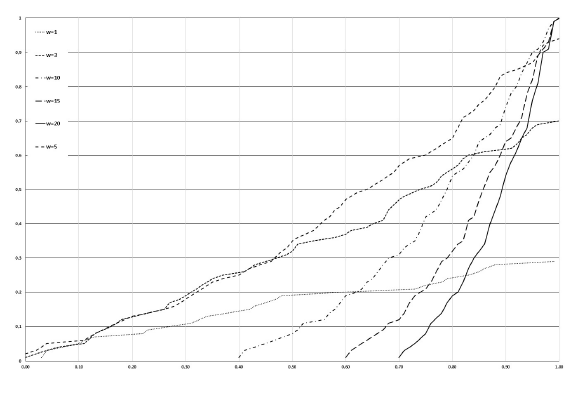
Figura 5 Graficas de la evolución de la superficie de inclusión correspondiente a los resultados de las intersecciones de los voxels de los orlados de S1 y S2 para w= [1, 3, 5, 10, 15 ,20].
En relación a la posibilidad de analizar las oscilaciones que se establecía en el MOD original, en este caso se propone analizar la evolución de los porcentajes de la superficie S2 por encima (E) o debajo (D) del orlado de S1, lo cual se determina fácilmente con operaciones de álgebra de mapas sobre S1 y S2 y sus orlados. La Figura 6 muestra la evolución espacial de las áreas E y D en función de wi, y la Figura 7 las curvas de porcentaje de superficie correspondiente a cada una de ellas. Como se puede observar, la Figura 6 es complementaria a la Figura 4, dado que el sesgo se considera en las zonas sin intersección (bandas blancas en la Figura 4). Por su parte, en la Figura 7 se puede observar que, para una inclusión del 50% de la superficie, la semi-amplitud es de algo más de 2 m, sin embargo, la inclusión del 100% de la superficie ocurre para w=6 m, puesto que no existen atípicos y este último valor es mayor que el doble del primero (2x2), lo anterior significa que existe un sesgo apreciable. Además, dado que la curva que representa el área de S2 por encima de S1 siempre es superior a la que representa el área de S2 por debajo de S1, es evidente que el sesgo es positivo.
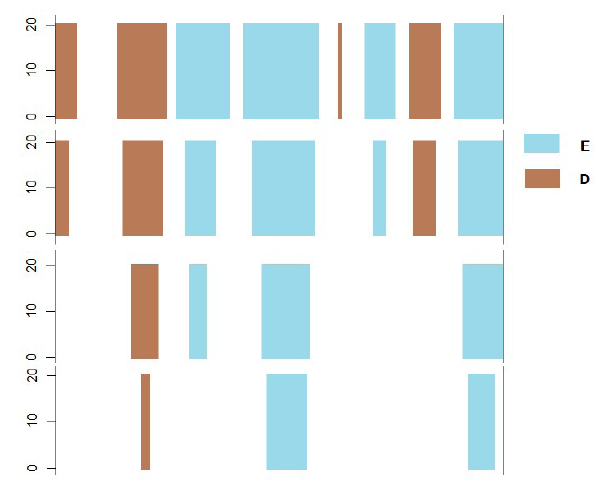
Figura 6 Evolución de las áreas de S2 que están por “encima” (E) o por “debajo” (D) de S1 para diferentes semi-anchuras de orlado w = [1, 2, 3, 4] m.
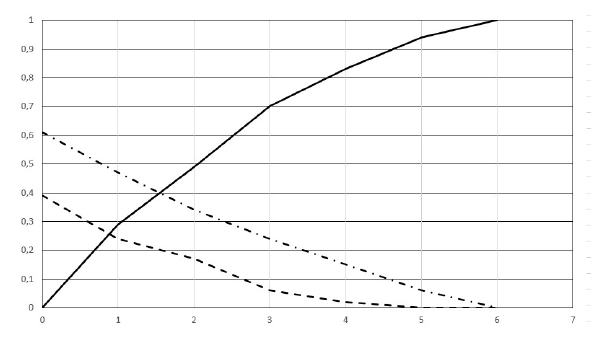
Figura 7 Evolución del porcentaje de área de S2 por encima (- · -) y debajo (- -) de S1, y dentro del buffer (-), para diferentes anchuras de orlado de S1 y S2.
Esto coincide plenamente con la percepción visual que transmite la Figura 2. Por su parte, la curva de superficie total que se presenta en la Figura 7 es en todo equivalente a la Figura 3, con la salvedad que aquí se orlan las dos superficies, y por ello el 100% de inclusión ocurre para la mitad de la semi-anchura indicada en la Figura 3.
4. Discusión
La discusión se va a centrar en distintos aspectos que consideramos clave analizar respecto a la propuesta de utilización de los métodos de orlado y que abarcan distintos ámbitos:
Conceptual. El salto de la aplicación de los métodos de orlado de líneas a superficies es bastante directo y los conceptos manejados son semejantes. Sin embargo, la aplicación del MOD a líneas conlleva cierto cambio dimensional, de 1D a 2D, que en nuestra propuesta debería haber llevado a un paso de 2D a 3D. Por simplicidad, y por ser más usual manejarnos con unidades de superficie que con unidades de volumen, se ha desarrollado esta perspectiva, la cual no invalida la posibilidad de aplicación del MOD al caso de MDE.
Algoritmos necesarios. La aplicación al caso de MDE de tipo grid es directa: operaciones simples de álgebra de mapas permiten ejecutar estos procesos sin problema, con agilidad y con grandes cantidades de datos. El trabajo con otros modelos de datos MDE requeriría codificar algoritmos más complejos.
Elemento de análisis. En este sentido existe un cambio radical respecto a los métodos de evaluación usualmente aplicados a MDE, y que se basan en puntos. El análisis basado en superficies nos parece más natural y cercano a la realidad que se desea analizar. Al igual que en el caso de aplicación a elementos lineales, los métodos propuestos permiten ser aplicados a una única superficie, o a un conjunto de superficies, con independencia de su extensión. Esto permitirá aplicar métodos de evaluación basados en control por parches, como se propone en el proyecto FunQuality4DEM (https://coello.ujaen.es/investigacion/web_giic/funquality4dem/).
Expresión de la incertidumbre. Dado que se obtienen curvas distribucionales, se dispone de mayor información sobre el comportamiento de la incertidumbre. Dado que ésta no se ajusta en la mayoría de los casos a una distribución normal, el disponer de curvas relativas a distribuciones observadas permite trabajar con percentiles de una manera directa. En el caso de desear la realización de un control de calidad (contraste de hipótesis), estas curvas se pueden utilizar como base de los métodos de control basados en tolerancias (una o varias tolerancias).
Capacidades de análisis. En relación a los resultados y posibilidades de análisis, los dos métodos de orlado son distintos, como ocurría en el caso de aplicación a datos lineales y sus resultados complementarios, pues presentan dos perspectivas distintas de una misma realidad. En general, los resultados del MOS son más sencillos de interpretar que los del MOD cuando sobre éste se adopta una perspectiva de intersección parcial de voxels. En cualquier caso, ambos métodos generan curvas semejantes a funciones de distribución observadas (globales o parciales). Esto ofrece una herramienta de análisis potente pues se visualiza qué ocurre en toda la población o sub población de interés. Además, el uso de estas funciones de distribución observadas, elimina la necesidad de la hipótesis de normalidad sobre las discrepancias y permite la aplicación de técnicas de control de calidad por medio de tolerancia(s).
Aplicabilidad del MOS y MOD. Consideramos que el MOS es más adecuado para el caso en que la exactitud de S1 es mucho mayor que la de S2, de tal manera que se pueda considerar despreciable. En el caso de los análisis de exactitud posicional por puntos se considera válida esta circunstancia cuando su exactitud es, al menos, tres veces mejor. Consideramos que el MOD es más adecuado para el caso en que la exactitud de S1 y S2 son aproximadamente iguales. En cualquier caso, el MOD permitiría, con gran facilidad, el considerar w distintas para S1 y S2, por ejemplo, si se vinculara w con una estimación de la desviación en cada una de las dos superficies.
5. Conclusiones
Este trabajo propone de manera pionera el uso de métodos de orlado para la evaluación altimétrica de MDE. Los métodos de orlado se han originado en el ámbito de la evaluación de elementos lineales, donde su uso está consolidado, pero no extendido. La aplicación de los métodos de orlado al caso de los MDE es una consecuencia lógica puesto que, en principio, son más adecuados para tratar realidades continuas y donde es difícil encontrar “puntos fácilmente identificables y bien definidos” como se requiere en los estándares de exactitud posicional.
La aplicación de los métodos al caso de MDE grid es bastante directa, si bien requiere algo de adaptación para el MOD pero, en todo caso, se resuelven con sencillas operaciones de álgebra de mapas. Los resultados del MOS permiten una relación directa con métodos de control posicional ya desarrollados, y que se basan en control por tolerancias aplicando multinomiales. Además, la curva de inclusión de superficie por orlado permite sacar conclusiones sobre la presencia de atípicos y sesgos. Los resultados del MOD son más ricos y complejos que los del MOS dado que se juega con el grado de intersección de los voxels de los dos orlados, lo cual permite una interpretación probabilística sobre el porcentaje de inclusión de las superficies que, además, puede ayudar a la interpretación visual. Este método también permite analizar la presencia de sesgos. Los resultados de ambos métodos son complementarios a los ya existentes y basados en parámetros (p.ej. la raíz del error cuadrático medio, media, desviación, etc.). Además, consideramos que presentan una perspectiva más rica al ofrecer una visión más amplia de lo que ocurre por medio de curvas distribucionales (Figura 3, Figura 5 y Figura 7).
El trabajo aquí presentado es una primera aproximación y por ello se basa en datos sintéticos en cantidad y tipología limitada. Junto a la ampliación de estas pruebas, queda también pendiente la aplicación al caso de datos reales.











 nueva página del texto (beta)
nueva página del texto (beta)



