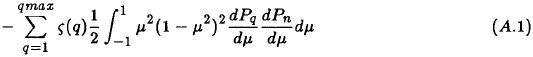
Appendix 1

All the terms are expressible in the form

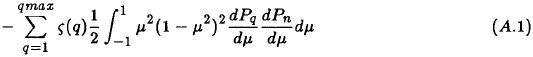
where q is the running variable and n is fixed. Note that in (A.1) we have already integrated by parts. Once we have used the differential formula in (2.4) we find the following result:

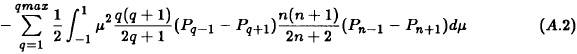
The next step is to use the second formula given in (2.5) on each of the two parentheses in (A.2). The following long formula gives the integral:

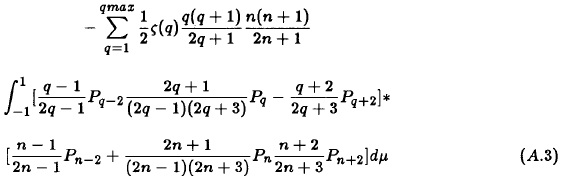
The remaining part of the evaluation is to use the orthogonality of the Legendre polynomials recalling that the integral of a product of two Legendre polynomials is zero except when the two indices are the same. If they are both n the value of the integral is 2/(2n+ 1). Paying attention to the minus sign in front we find the form given in (2.6) with the formulas for the coefficients following in (2.7).