APÉNDICE 1
MÉTODO PARA CALCULAR TENDENCIAS POBLACIONALES UTILIZANDO CONTEOS DE MIGRACIÓN
El objetivo de este apéndice es hacer una descripción metodológica detallada que permita replicar los análisis presentados en este artículo. Los supuestos y condiciones que preceden los análisis están descritos en la sección de Métodos. Para hacer estas estimaciones, se recomienda utilizar series de al menos 10 años de datos; series de datos de mayor duración hacen las estimaciones más robustas y precisas.
Este método tiene dos etapas: (1) el cálculo de índices anuales de abundancia, que obtiene la media del número de aves registradas por día, y (2) la determinación de tendencias a largo plazo, que obtiene una estimación anual del porcentaje de cambio poblacional. Este apéndice es una modificación al método recientemente publicado por Farmer et al. (2007) y adaptado para permitir la combinación de los censos de dos (o más) localidades independientes que operan de manera simultánea.
1. ÍNDICES ANUALES DE ABUNDANCIA
Los censos diarios de la migración son influenciados por variables como fecha y estado del tiempo y por ello los censos durante la migración exhiben una distribución marcadamente sesgada, con muchos días en que los censos tienen resultados bajos o moderados y pocos días en que los censos reportan muchas aves. Un índice anual basado en la suma o en la media aritmética de los censos diarios estaría inapropiadamente influenciado por la magnitud de los censos elevados cada año, por tanto, se espera que el cambio anual afecte todos los censos diarios de la misma manera y no solo a los días con censos elevados.
Conteos de migración de rapaces. Para desarrollar los índices anuales, se utilizan censos colectados por hora de observación. El total de horas de observación (en adelante "observación diaria") varía día a día y a través de los años en cada sitio de monitoreo. Para cada especie, los autores identificaron el periodo del día que incluye al 95% de las rapaces registradas ese día (en adelante "periodo diario"). Se excluyen de estos análisis los individuos registrado fuera de este periodo diario. En días en que hay una cobertura incompleta en el campo durante la observación diaria, se estima el valor del periodo diario como N= C*H/h, donde C es el censos durante el total de horas de observación, h el número de horas de observación y H el número de horas del periodo diario.
También se ajustaron los censos a través del cálculo de un "periodo estacional" para los días de la temporada que incluyen el 95% de los individuos de cada especie. El incremento del número de días de censos conteos en un mismo lugar a lo largo de los años puede incrementar la frecuencia de los censos bajos, produciendo tendencias espurias en los índices anuales. La utilización de periodos estacionales que incluyen el 95% de las rapaces registradas tiene dos efectos principales: (1) reduce el efecto de cambios en los periodos de muestreo en el campo, y (2) elimina los días en que se registran cero individuos de una especie al inicio o al final de la temporada de campo, que de otra manera contribuyen a una distribución inaceptable de los residuos en una regresión.
Estado del tiempo. La dirección y la velocidad del viento son dos variables que afectan directamente la concentración de rapaces en migración registradas en lugares de censos migratorios (Mueller & Berger 1961; Haugh 1972; Richardson 1978; Newton 1979; Kerlinger 1989).
La mayoría de estos lugares colectan información de estas variables del tiempo o ésta está disponible en bases de datos de clima disponibles en Internet. Estos datos pueden ser utilizados como covariables en los análisis, sin embargo Hussell (1981), Francis & Hussell (1998) y Farmer & Hussell (2008) han hecho pruebas con la inclusión de estas covariables en los análisis de 22 localidades de censo de migración en Norteamérica y encontraron que la inclusión de estas variables en los índices anuales no tiene ningún efecto en los índices obtenidos (Alien et al. 1996; Farmer et al. 2007, 2008a; Smith et al. 2008a, 2008b).
Obtención de índices anuales. En este artículo se utilizan regresiones múltiples para derivar índices de población (media geométrica) que permiten compensar por días sin datos y en algunos casos covariables del tiempo (e.g. dirección y velocidad del viento). Los aspectos básicos de este método han sido descritos por Hussell (1981), Francis & Hussell (1998) y Farmer et al. (2007) y son descritos aquí en detalle para presentar algunos ajustes que permitan su aplicación a las particularidades de este análisis.
Los índices anuales obtenidos son: (a) la media geométrica de los conteos diarios ajustada según la fecha (en delante "ajustados según la fecha") o (b) la media geométrica de los conteos diarios ajustada según covariables de viento (en adelante "ajustados según el viento"). Estos índices son estimaciones de la media anual de los conteos diarios, derivados de los valores aportados por la regresión de la media geométrica del conteo diario, y ajustados según las covariables. El modelo completo, con todas las covariables, es:
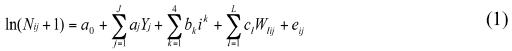
donde Nijes el número de individuos de una especie que fueron contados (o estimados) durante las horas de observación del día i en el año j, Yj es la serie de J variables simuladas, a las que se asignó el valor 1 cuando el año=j y cuando fueron cero en los años restantes (los valores de j varían de 0 a J representando una serie de J+1 años; no hay variable simulada para el año 0), ik son términos de fecha del primer al cuarto orden, Wlij es el valor de la variable del tiempo l en el día i en el año j, α0 es la intersección estimada por la regresión representando los efectos de cada variable independiente en el 1n(Nij+1), y finalmente eij representa la variación sin explicación. El modelo de regresión es un Análisis de Covarianza (ANCOVA) de un factor, con el periodo anual como factor (variable categórica) y todas las demás variables independientes como covariables.
Los análisis de regresión fueron ponderados en proporción al número de horas de observación de cada día, hij. El método para obtener los índices de media geométrica es similar a otros utilizados anteriormente (Hussell 1981; Francis & Hussell 1998), con la diferencia de que cada índice es expresado como la media estimada del conteo diario (Farmer et al. 2007), en vez de la media estimada del conteo en un día "típico" (derivado de la media ajustada en la escala transformada).
Los índices ajustados según la fecha y ajustados según viento y fecha fueron derivados de cada serie de datos de censo. En la mayoría de los casos, el índice ajustado según la fecha tiene mejores resultados, de acuerdo a los criterios descritos por Farmer et al. (2007).
El índice ajustado según la fecha fue estimado del modelo de regresión que incluye sólo los términos año y fecha, e.g.:
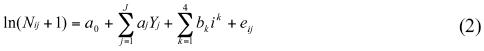
Este índice fue diseñado para eliminar los sesgos provocados por los días en que no se colectaron datos en el campo. Posteriormente, se calcula la media geométrica estimada del conteo (transformada a la inversa) para cada día en cada año, obteniendo la suma de cada año durante el periodo estacional, y este valor es dividido entre el número de días en el periodo estacional, retransformado para obtener la suma de los índices ajustados según la fecha (SAF)j, sumados al error de la varianza de la regresión (V/2) de esta manera:
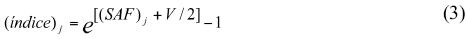
Debido a que los conteos en Veracruz son hechos desde dos localidades, Chichicaxtle y Cardel, que representan muestras independientes del mismo flujo de rapaces migratorias a manera de una línea de muestreo, el modelo para combinar los conteos de estos dos sitios es:
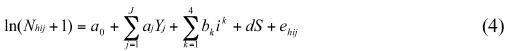
donde Nij es el número de individuos de una especie contados (o estimados) durante el periodo diario en la localidad h, en el día i, en el año j, S es la variable simulada cuyo valor fue asignado a 0 y a 1 para las observaciones en las localidades 1 y 2 respectivamente, d es el coeficiente estimado de la regresión, eij que representa la variación no explicada y el resto de las variables y coeficientes son los mismos que los utilizados en el modelo general, descritos anteriormente (ecuación 1). Por tanto, este modelo asume los mismos efectos anuales en ambas localidades en todas las fechas para cada especie y los mismos efectos de localidad a lo largo de todos los años y fechas, todos los cuales tienen un efecto aditivo en la escala transformada (y aproximadamente multiplicativo en la escala original). En ambas localidades, este supuesto fue probado a través de los resultados de interacciones año*localidad.
El índice ajustado según la fecha fue calculado de la misma manera en que se explicó anteriormente (ecuación 3), con una excepción: la media geométrica estimada del censo (transformada a la inversa) para cada día en cada año fue ajustada para obtener una estimación del censo en una localidad hipotética "promedio", asignando a S el mismo valor de su media ponderada a lo largo de la serie de datos anuales disponible.
El índice ajustado según viento y fecha se obtiene de la misma manera que el índice ajustado según la fecha, con la adición de 12 variables que incorporan dirección y velocidad del viento (E, SE, S, SW, E2...SW3, representados como 
en el modelo de regresión). Sin embargo, para este índice, la media geométrica estimada del conteo (transformada a la inversa) para cada día de cada año es calculada asumiendo que el valor de cada variable de viento en todos los años es igual al valor promedio de esa variable en la serie de datos.
2. DETERMINACIÓN DE TENDENCIAS POBLACIONALES
Las trayectorias de los índices anuales fueron estimadas como la media de la tasa geométrica de cambio sobre un intervalo de tiempo definido (Link & Sauer 1997). Las trayectorias fueron analizadas mediante una regresión polinomial aplicada a la serie de índices anuales [ln (índice),]. Para reducir las correlaciones entre los términos polinomiales, cada regresión fue centrada en el año al medio de la serie de datos.
El modelo polinomial de mejor ajuste a la serie de datos fue seleccionado para cada especie siguiendo un procedimiento de tres pasos: (1) para evitar un ajuste excesivo, el número de modelos posibles fue limitado de acuerdo a la longitud de la serie de coeficientes de regresión
Las estimaciones de las tendencias y su valor significativo fueron obtenidas reparameterizando los términos anuales (Francis & Hussell 1998). Este método toma en consideración la trayectoria dentro de la serie de datos anuales comparada y usa la varianza alrededor de la trayectoria total y provee mayor poder estadístico para la detección de tendencias que las regresiones lineales que no se ajustan a la trayectoria de los índices anuales. La reparametrización transforma los términos anuales, de manera que el término de primer orden estima la tasa de cambio entre dos conjuntos de años y por tanto es equivalente a la trayectoria de una regresión log-lineal. Este método es aplicable a otras series de datos que se ajustan a los supuestos que se describen en la sección de Métodos, como los conteos obtenidos en estaciones de censo y anillamiento en migración de otras especies.